基于姿态角递增算法的6轴机器人通用运动规划方法

程 晗，王 内，寿晓波

（中国船舶重工集团公司第722研究所，武汉 430000）

0 引言

目前，针对机器人的运动学分析研究最多的是基于成熟的机器人产品如ABB IRB系列机器人等平面连杆构型的机器人[1～3]。对于更具有通用性的非平面连杆构型机器人系统却研究较少，如前3关节轴线所在平面和后3关节所在平面有偏置的6轴机器人。

相较平面型机器人的正/逆运动学分析，本文建立一种更具通用性的6轴串联式机器人正/逆运动学方程，结合机器人的结构参数，可以在机器人的运动控制中更加快速的进行运动学的求解。同时，针对这种平面偏置型6轴机器人，根据机器人末端运动轨迹的要求，建立一种基于等效转轴和等效转角的通用运动轨迹规划方法。

1 通用6轴工业机器人的结构分析

常见的串联式垂直多关节（一般为6关节）的机械臂的3D构型如图1所示。

图1 6轴串联式机械臂3D构型

通用串联构型的六轴机械臂的主要结构参数如图2所示，相对于目前常见的机械臂构型如《论文1》中所述机器人，也即一般考虑机械臂的构型的简化连杆模型是在同一个平面内。本文中在通用串联构型的六轴机械臂引入了参数P7，使得平面连杆构型变为空间构型。

图2 空间构型的通用机械臂主要结构参数

图2中P1和P6用于确定世界坐标系和工具坐标系用，故下文中的正反解的解析表达式中没有涉及。针对以上通用的6轴串联机械臂构型，可以建立统一的运动学正反解标准方程。

2 通用6轴工业机器人的运动学分析

首先按照D-H连杆坐标系建立的一般规则，首先确定各个坐标系的X、Y、Z轴的方向和原点坐标，从而建立该通用6轴机器人的D-H坐标系。各关节的D-H坐标系的建立如图1所示。

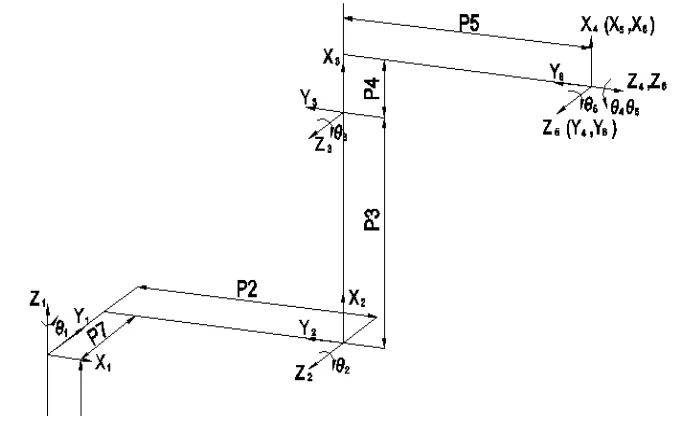
图3 通用6轴机械臂的各连杆坐标系

假定基座标系和轴1的坐标系建立在同一点上的情况下，6轴机器人D-H坐标系下各个连杆和关节参数可以列出，如表1所示。

表1 通用6轴机器人的D-H坐标连杆参数表

2.1 正运动学分析

机器人的正解指的是通过机械臂的关节角求解出腕点的空间位置和姿态的过程，腕点的空间位姿（位置和姿态）我们使用D-H坐标来表示。

利用表1即机械臂D-H参数表中的数据很容易求得机器人末端也即轴6的坐标系{6}相对于基座标系{0}的位姿矩阵为：

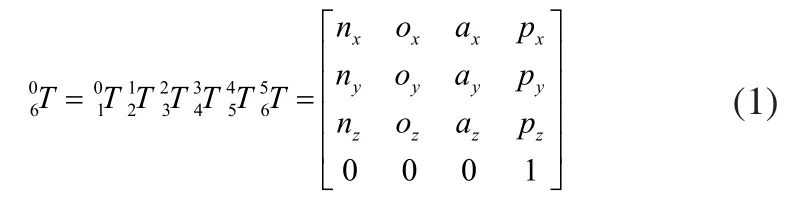
式中：

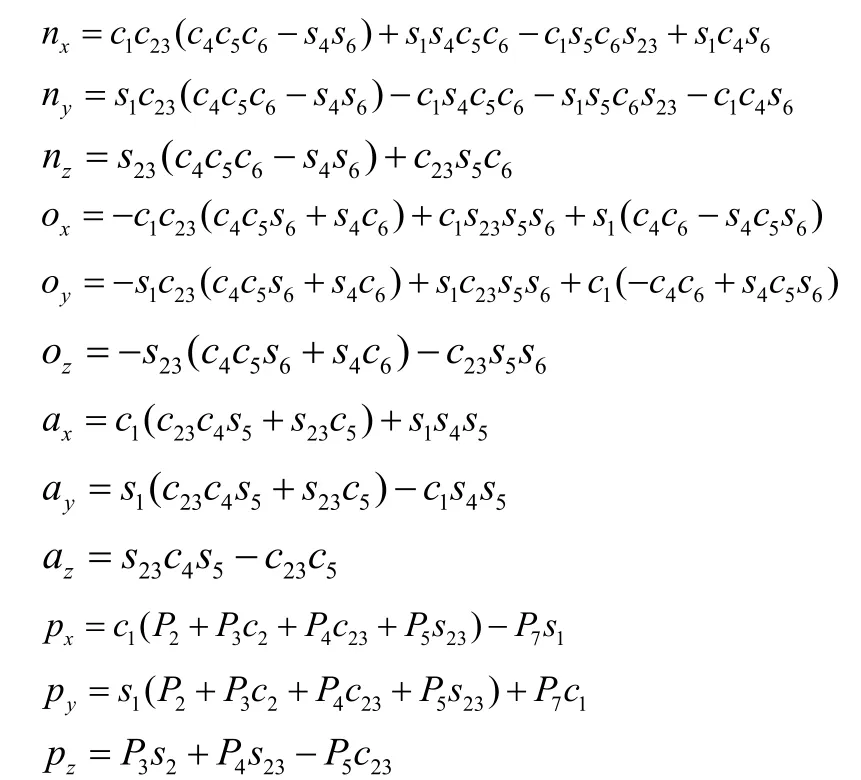
为校核所得结果的正确性，计算当θi取表1中的初始值{0,90°,0,0,0,0}时，计算结果为：

与机械臂结构简图即图1中显示的结果完全一致，说明这种通用机械臂运动学正解的解析表达式是准确可靠的。

2.2 逆运动学分析

根据机械臂运动学可得封闭解的Pieper准则，这种通用6旋转关节的机械臂构型由于最后3轴交于一点，所以可用反变化法（也称代数法）得封闭解如下：

将式子：

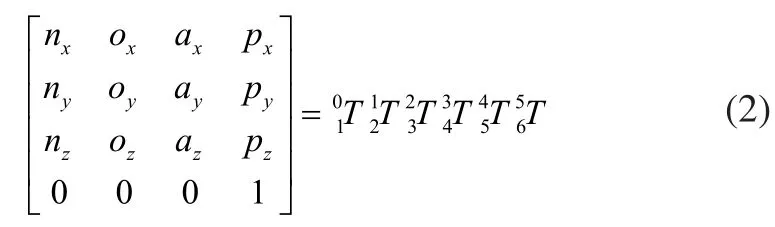
同时有，令两边矩阵的（1，3）和（3，3）元素分别相等，得到：

3 姿态角递增规划算法

不同于3轴或4轴工业机器人（如码垛用机器人等），6轴机器人的运动轨迹规划不仅需要控制工具末端TCP点的位置量即px、py、pz沿着规划轨迹精准运动，同时也要保证工具的姿态按照预定义的运动姿态规划进行实时变化。

例如以下的简单直线插补过程，2个实线模块表示的是工具起点和终点位姿，姿态角递增规划算法的目的是为了保证工具末端TCP点的位置和姿态能按照预定义的姿态规划路径逐渐精确地从起点位姿运动到终点位姿。

图4 姿态角递增的直线插补方式

鉴于齐次坐标的姿态矩阵即R3×3矩阵中共9个变量相对于3个姿态量过于冗余，故目前常见的姿态规划方法主要是基于欧拉角、RPY角、四元数或者旋转变换通式等，本文提到的运动控制算法主要采用的是基于旋转变换通式的姿态角递增规划算法。

易得：

上述式子即为旋转变换通式的建立过程，反向问题则是依靠旋转变换矩阵求解等效转轴k和等效转角θ。

对于任意给定的旋转矩阵：

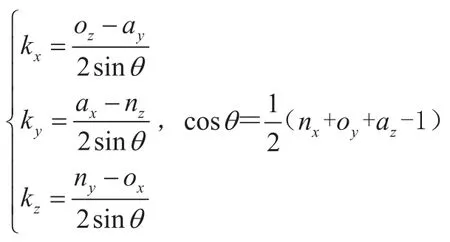
依据以上2个式子，可以很容易求得任意给定的旋转矩阵的等效转轴k和等效转角θ，插补过程中任意插补点的位姿矩阵为：

其中PΔ表示起点到终点的位置变化矢量，N表示依据运动步长规划的插补步数。

姿态角递增规划算法的主要计算流程如图5所示。

图5 姿态角递增规划算法流程

4 仿真及结果分析

根据前述6轴机器人运动学算法和运动轨迹规划算法，选定初末关节角1到6关节角度值分别为：{5°,26°,86°,12°,13°,30°}和{10°,51°,101°,33°,26°,47°}共两点作为直线运动轨迹规划的起点和终点的位姿。

运用上述方法规划的TCP点直线运动轨迹如图6所示。

图6 规划的TCP点末端位置

各关节的运动变化曲线如下图所示，其中蓝色细实线表示关节1（axis1），绿色细虚线表示关节2（axis2），红色短划线表示关节3（axis3），蓝色粗实线表示关节4（axis4），绿色粗虚线表示关节5（axis5），红色粗短划线表示关节6（axis6）。由图可知，经规划算法之后关节1至关节6的起点和终点的角度值和规划前的值一致，说明规划算法能保证机械臂从起点运动到终点。

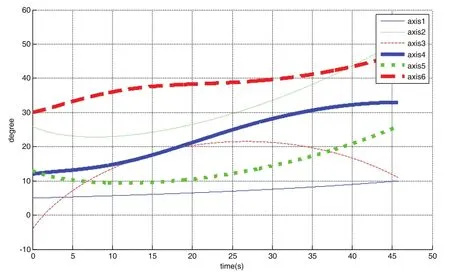
图7 各关节角度变化序列

TCP点坐标系的三个轴变化如图所示。其中绿色曲面为TCP点坐标系X轴分量的变化过程，红色曲面表示TCP点坐标系Y轴分量的变化过程，蓝色曲面表示TCP点坐标系Z轴分量的变化过程，黑色直线表示TCP点坐标系原点位置的变化。

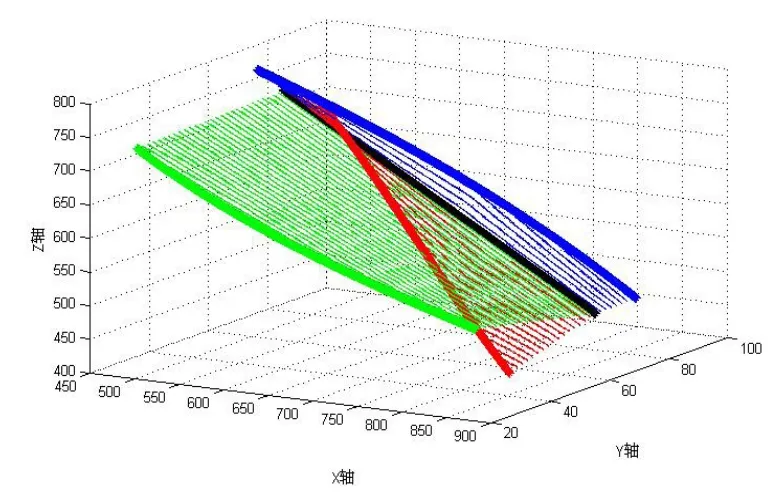
图8 TCP点姿态变化示意图

由图可知，TCP点坐标系的位置和姿态变量经过姿态角递增算法规划后能逐渐从初始位资连续运动到终点位姿，变化过程平滑、连续且稳定，证明了这种姿态角递增算法在通用型6轴工业机器人运动位姿规划过程中的可靠性。

5 结论

本文在通用6轴工业机器人运动学分析的基础上，建立了基于姿态角递增算法的位姿轨迹规划方法。该方法不仅适用于目前常见的平面构型的机械臂，同时也能适用于前3关节和后3关节旋转轴平面产生偏置的非平面构型的通用串联式6轴机械臂，具备较高的普适性。正逆解过程和姿态角递增算法均利用解析表达式描述，因而可以很方便地在机器人控制系统中实现编程控制，而且有助于提高控制系统的实时性。

[1] Paden B,Panja R.1998.Globally stable‘PD+’,controller for robot manipulators[J].International of Control,47:1697-1712.

[2] 蔡自兴.机器人学[M].北京:清华大学出版社,2000.

[3] 孙迪生.王炎.机器人控制技术[M].北京:机械工业出版社,1998.

[4] 李磊.六自由度并联平台运动规律及控制方法研究[D].哈尔滨工业大学.2007.

[5] 门昌华,关学锋,等.基于PMAC的六自由度机器人开放式控制系统开发[J].机电产品开发与创新.2008(7).

[6] 张兰芳.基于VC++开发的并联六自由度测控系统[D].浙江:浙江大学,2002.

[7] L.S.Farhy.Modeling of oscillations of endocrine networks with feedback[J]·Methods Enzymol.2004(384):54-81.

[8] Delta Tau Data system Inc.PMAcAccEssoRY 8s[M].1997.

[9] 刘敏杰.并联机器人动力学与自适应控制技术研究[D].上海:上海交通大学,2001.