蚁群算法中参数优化及其仿真研究

魏 星，李 燕

（桂林航天工业学院 信息工程系，桂林 541004）

0 引言

2 0世纪9 0年代初，蚁群算法由意大利学者M.DORIGO[1]等人提出。算法采用正反馈机制，易于发现较好解，并且蚁群算法具有很好的通用性和鲁棒性。因此，国内外很多专家学者充分利用蚁群算法的优点解决NP-hard问题，特别是旅行商问题、网络路由规划等组合优化问题。但是，在蚁群算法中，参数值的选择直接决定了算法的好坏，而算法中不仅参数的个体取值十分重要，并且参数之间的组合取值更是直接影响着整个算法的结果，如果参数取值不当，会导致算法陷入局部最优等问题。

针对基本蚁群算法参数取值问题，分析算法参数的设置，提出各参数之间的最佳优化组合方案，并进行了仿真实验，实验结果证明了该改进方法提高了算法的效率，对蚁群算法的应用有一定的参考意义。

1 基本蚁群算法

蚁群算法是一种智能随机搜索算法，多用于解决离散问题，算法的解是一个从初态到终态的序列，算法得到的最优解即为最优状态转移序列。在算法中蚂蚁是根据系统路径上的信息素强度完成状态转移，蚁群中每只蚂蚁进行一次路径搜索后，都会更新一次路径上的信息素强度，进而整个蚁群进行一次更新，随着更新搜索过程的重复，通过各个蚂蚁的相互协作，最优路径上的信息素强度最大，该序列即为最优解。

蚁群算法基本模型如公式(1)所示[1]：

算法执行时，在n个节点上随机放置m个蚂蚁，每条节点间路径都设有一个信息素初值τij(0)，另外，为了记录蚂蚁走过的城市信息，设定Tabuk为状态序列转移表。算法规定，每只蚂蚁根据公式(1)随机进行状态转移，并且约定只能由Si转移到某个相邻状态Sj。状态转移概率pij(t)的公式：

其中：τij(t)为两节点i、j之间的路径信息素，ηij(t)为节点间距离因子，α为信息素重要程度，β为启发因子重要程度，α和β均大于0，allowedk为允许蚂蚁经过的集合。

信息素更新如公式(2)所示：

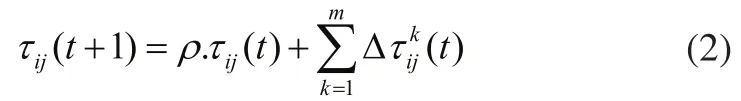
其计算公式为：

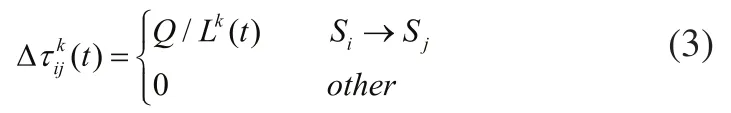
其中：Q是一个常数，是蚂蚁某时刻经过的路径长度。其值越小，表明信息素强度越大，更多蚂蚁会通过相互通信移动到此路径上，最后算法得到全局最优解。

2 算法参数的最优选择及实验分析

从前文的分析不难看到，在蚁群算法中，算法性能会受到α、β、ρ、m、Q等基本参数取值的影响。但是，通过大量的数学计算和分析，参数选择尚无严格的理论依据，因此，本文先采用一些文献提出的参数[3～6]，通过逐步调整各个参数的取值，再进行一系列的仿真实验，找到蚁群算法中最佳的参数选择。为方便实验数据进行比较，本文后面的仿真实验研究都是以Oliver30城市问题为例，利用蚁群中ant cycle system模型研究参数对最优路径的影响。

2.1 启发因子α和期望值启发式因子β的影响分析

在算法中，启发式因子α描述搜索随机性，期望值启发因子β表示确定性因素大小，两个因子既相关又矛盾。α取值越大，重复搜索可能性越大，从而导致随机性降低，α取值较小，随机性增强，但收敛速度变慢；β取值越大，局部最短路径选择的可能性越大，收敛速度变快，但随机性降低，β取值较小，算法最终陷入随机搜索，无法找到最优解。

因此，既要加快蚁群算法收敛速度，又要找到全局最优解，就必须使蚁群的搜索过程具有很强的随机性，同时具有快速的收敛能力。

在蚁群算法的实际应用中，通过实验分析可以确定启发式因子α及期望启发因子β取值。实验中的参数取值为：蚂蚁循环一周所释放的总信息量Q=400，信息素衰减因子ρ=0.7，蚂蚁数m=20，循环次数N=10，表1描述了参数α、β的取值对算法性能的影响，其中：平均值表示算法运行10次的最短路径长度的平均值；最优值、最差值分别表示算法运行10次最短路径中的最小值和最大值。

表1 参数α、β的取值对算法性能的影响表

通过观察表1中的实验结果，我们不难看出，在蚁群算法中，选取不同值的启发因子α和β，将会对算法的搜索性能产生很大的影响。其中，当α=1，β=4时，算法取得的平均值及最优值都是最好的。另外，我们可以看到，取值在适当的范围内，即使选择α和β值时有不同的参数组合，但相比较而言，实验结果表明蚁群算法也能获得较好的结果，并且算法的收敛速度也相当接近。在ant cycle system模型中，结合实验结果，我们可以得出：在本文的问题中，选取α∈[1.0,3.0]，β∈[2.0,5.0]范围时，算法性能较好。

2.2 信息素挥发因子ρ的影响分析

同前文分析一样，算法还受到另外一个参数——信息素挥发因子（用1-ρ表示）的影响[3]。信息素挥发度的取值直接影响到算法的全局搜索能力及收敛速度，如果1-ρ取值很小，随机性增强，但收敛速度变慢，这时算法正反馈比较弱；如果1-ρ取值较大，重复搜索可能性越大，从而导致随机性降低，影响算法全局搜索性能。

在实验中，参数取值为:蚂蚁循环一周所释放的总信息量Q=400，α=1，β=4，蚂蚁数m=20，循环次数n=10，其中：表中平均值表示将10次运行中每次得到的最短线路长的平均值。图1表示了信息素挥发因子ρ在不同取值下，对算法性能的影响。

图1 参数ρ对算法的性能影响图

从图1中不难看出，ρ的取值对算法的结果影响较大。当ρ<0.5时，收敛速度较快，但搜索结果较差。当ρ>0.8时，搜索结果较好，但收敛时间成几何级数增长，实用性较差。由图1可知，取值ρ∈[0.5,0.8]，算法的的全局搜索能力较强，收敛速度较快。

2.3 α、β、ρ三种因子组合对算法性能的影响分析

前文分别对α、β、ρ三种因子取值对算法的性能影响进行了分析，但实际上蚁群算法中各参数α、β、ρ的作用是紧密耦合的, 单个参数最优，但将其组合起来未必会取得好的效果。如果α、β、ρ的参数取值不合适，会导致算法求解速度很慢，并且解的质量很差。下面我们就α、β、ρ三种因子的组合进行实验研究，以达到最佳组合配置。

根据前文是实验分析，就本文研究而言，α、β、ρ三种因子的最佳取值范围分别为：α∈[1.0,3.0]，β∈[2.0,5.0]，ρ∈[0.5,0.8]，因此，我们的实验数据取值就在此范围内进行微调，以达到理想的数值。实验仍以Oliver 30城市问题为例，有关算法参数为：蚂蚁循环一周所释放的总信息量Q=400，蚂蚁数m=20，循环次数n=10，实验结果如表2所示。

表2 参数α、β、ρ组合对算法性能的影响

从表2可以看出，三个参数的取值都不收敛到某个具体的数值，这是由于蚁群算法属于随机搜索算法，因此得到的结果也是随机的，所以不可能产生收敛的结果。另外，根据表2中数据，我们可以确定在本文的实验中，最佳的三个参数组合为实验组次中的第3组，即：α=1.5，β=4.1，ρ=0.64，这时，算法的最优值和平均值也是最好的。

2.4 蚂蚁数量m和信息量Q的影响分析

在算法中，两个参数——蚂蚁数量m和信息量Q对算法性能也有影响。

对于蚁群数量m对算法性能的影响，也可以通过实验来进行详细的分析。在实验中，我们选取有关参数为：蚂蚁循环一周所释放的总信息量Q=400，信息启发式因子α=1.5，期望启发式因子β=4.1，信息素残留常数ρ=0.64，蚁群计算中，如果相邻两次搜索的最优解误差小于0.001[5]，算法停止。蚂蚁数量选取集合为：m∈{5,10,15,20,25,30}。实验结果如图2所示。

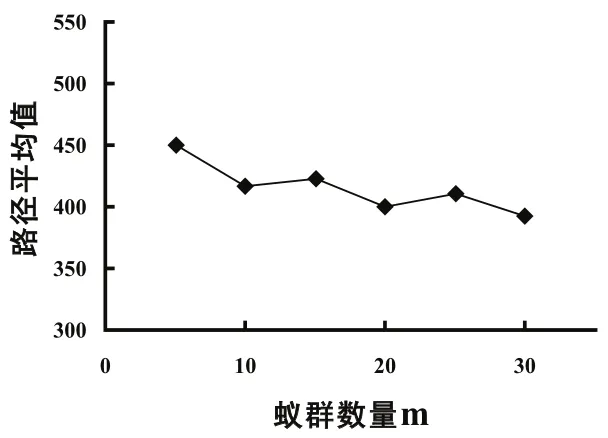
图2 蚂蚁数量m对算法性能影响图

由图2可见，蚂蚁数量对蚁群算法收敛性能的影响基本呈线性规律，当蚂蚁数量m=30时，模型可以在较少的迭代次数内找到一个最佳的最优解。所以，在蚁群算法中，蚂蚁数量m过大，虽然搜索更加稳定，也提高了全局性，但是减慢了算法收敛速度；而蚂蚁数量m过小，随机性减弱，全局性能下降，路径上的信息量逐渐减小，最后趋于0，最终算法容易出现过早停滞的现象。所以，通过仿真实验验证，m的取值为[ ,2]n n 的一个整数时，算法性能较好。

另外，总信息量Q是蚂蚁循环一周后，释放在其经过路径上的信息素总和。Q越大，算法的收敛速度越快。但是，当Q特别大时（Q>2000），此时算法容易陷于局部最优解，算法的性能下降。因此，在实际应用中，我们一般取Q<2000，此时，算法既有较快的收敛速度，性能也较好。

3 结束语

本文在研究基本蚁群算法模型的基础上，通过一系列仿真数值实验，利用大量的数据分析了算法中α、β、ρ、m和Q等参数的不同取值对算法性能的影响。通过仿真实验验证，提出了最优参数组合方法，对于大多数蚁群优化问题而言，本文提出的参数优化方法都能使算法快速、有效地找到全局最优解，提高了算法的效率，对蚁群算法的应用有一定的参考价值。

[1] Dorigo M, Maniezzo Vittorio, Colorni Alberto. The Ant System: Optimization by a colony of cooperating agents.IEEE Transactions on Systems[J].Man, and Cybernetics-Part B,1996,26(1):1-13.

[2] 魏星,周萍.改进型蚁群算法的语音动态规划研究[J].计算机仿真,2011,28(5):402-405,409.

[3] 刘利强,戴运桃,王丽华.蚁群算法参数优化[J].计算机工程,2008,34(11):208-210.

[4] 詹士昌,徐婕,吴俊.蚁群算法中有关算法参数的最优选择[J].科技通报,2003,19(5):381-386.

[5] 甘屹,李胜.蚁群算法的参数优化配置研究[J].制造业自动化,2011,33(3):66-69.

[6] 刘伟.蚁群算法中求解参数最优选择分析[J].电脑与信息技术,2011,19(1):10-12, 66.

[7] 王娟,巩建平,冯蕾洁.一种改进的遗传蚁群混合算法[J].制造业自动化,2014,36(2):79-80.

[8] 陈志雄,潘耘,李嫣,李晋凯.用改进蚁群算法求解无线传感器网络多sink节点关联问题[J].计算机应用与软件,2012,29(2):246-249.

[9] 田钧.基于改进蚁群算法的物流配送应用研究[J].制造业自动化,2013,35(8):88- 90,109.