不同激励方式对有界空间超声场分布的影响

闫 晶，朱菲菲，张明铎，郑保宁，李洋洋

(陕西师范大学 物理学与信息技术学院，陕西省超声学重点实验室，陕西 西安 710119)

不同激励方式对有界空间超声场分布的影响

闫 晶，朱菲菲，张明铎*，郑保宁，李洋洋

(陕西师范大学 物理学与信息技术学院，陕西省超声学重点实验室，陕西 西安 710119)

根据波的叠加原理分析了矩形空间的超声场分布，并对不同激励方式下的声场分布进行了实验研究。结果发现:单频正弦信号激励时，声源频率越高，声场分布越均匀；多频合成信号激励时，由于声波间的不相干性，声场的空间均匀性比单频信号激励时有显著改善，且频率越高，改善效果越明显。研究表明：就改善声场均匀性而言，应结合超声系统的谐振特性合理选择合成信号的带宽。

单频信号；合成信号；超声场分布；均匀性

PACS: 43.35.+d

在大功率超声技术的各类应用中，声场分布特性[1-3]对应用效果的影响一直受到重视，其中相当一部分应用对声场的均匀性有一定的要求。为了改善声场均匀性，人们进行了各种尝试，如改变槽体形状形成扩散声场[4]、改变换能器的布阵方式[5-8]、设计薄板弯曲振动共振辐射器[9]来改变声波的辐射方向、采用复频或调频方式减少声场中的驻波[10-14]等。文献[4-9,14]所述方法实施起来结构和工艺复杂，而文献[10-13]所述调频方式在系统工作的任一瞬间实际上只有一个频率，复频方式一般是2～3个频率。本文针对应用较多的矩形槽式换能振动系统结构的谐振特性，从激励信号着手，利用具有一定带宽范围的多频合成信号激发，不仅结构简单，效果更为理想。

1 理论分析

根据波的叠加原理[15]，同频、固定相位差的两列波在空间相遇时：

p=p1+p2=pacos(ωt-φ)。

(1)

式中

p1=p1acos(ωt-φ1),

p2=p2acos(ωt-φ2)，

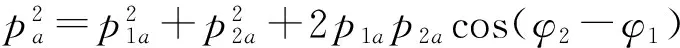
ω为声源振动的圆频率。合成声场的平均能量密度为

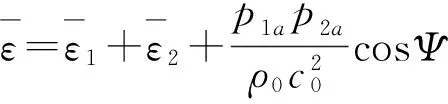
(2)

其中ρ0为空间媒质密度，c0为声波传播速度。由(1)、(2)式可以看出，同频合成声场的声压及平均能量密度与两列声波到达此位置的相位差Ψ有关。两列波以相同的相位到达时，合成声场的声压及平均能量密度最大；反之，声压及平均能量密度最小。

对于不同频率的两列波在空间相遇时，声场平均能量密度:

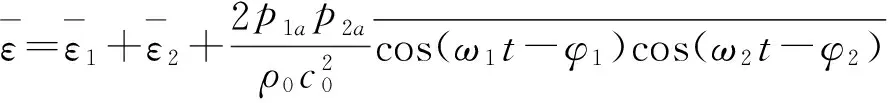
(3)

依据波动声学理论，频率为f的声源在有界空间激发的声场是由大量简正声波叠加而成的。大量简正声波叠加的结果，会在一定程度上“平均”掉驻波效应，使空间声场分布趋向均匀。频率为f的声源在一定矩形空间激发的简正声波总数为

(4)

其中V、S、L分别代表空间体积、壁面总面积、空间边线总长。由(4)式可知，声源频率越高，或者声场空间几何尺寸越大，简正波的数目越多，空间声场分布越均匀。

综上，通过不同频率声波的叠加或者增加声场中的简正声波数目(本文通过提高频率实现)，都可在一定程度上改善声场均匀性。

2 实验系统

实验用不锈钢板制成的矩形槽，其几何尺寸为280 mm×200 mm×185 mm，3种换能振动系统的谐振频率分别为23.94、36.08和56.77 kHz。换能器均匀分布在槽底，排列方式如图1所示，其中右侧的小圆表示排水口。

实验中，整套振动系统分别用两种信号激励，一种是正弦信号(频率为换能振动系统的谐振频率)；另一种是由多种频率的等幅正弦信号叠加而成的具有一定带宽的合成信号(中心频率为换能振动系统的谐振频率)，即

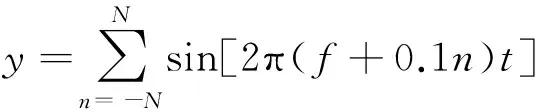
(5)

其中：f代表换能器振动系统的谐振频率，N=Δf/0.2(N为整数)，Δf为合成信号的频带宽度。由于相邻信号频率差别很小(0.1 Hz)，合成信号的频谱可以近似看作在f-Δf/2到f+Δf/2范围内是连续的。实验中Δf分别取1、2和3 kHz。

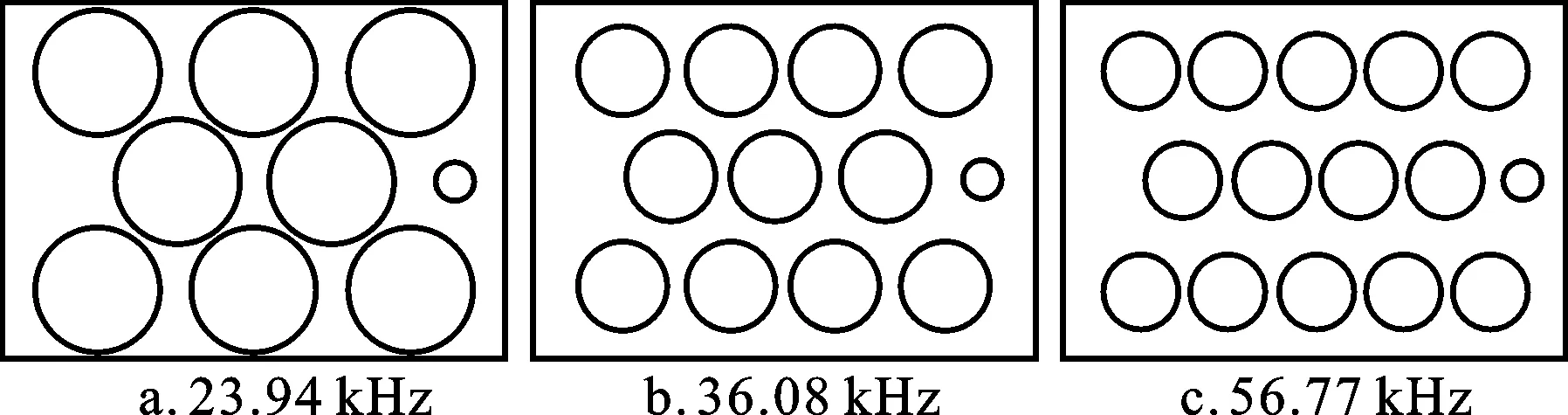
图1 矩形槽底部换能器排布方式Fig.1 The arrangement of transducers at the bottom of the rectangular groove

正弦激励时，信号由DG1022U型函数发生器直接产生。合成信号激励时，信号由计算机用Matlab软件编程产生(采样频率为409 600 Hz，时长为10 ms)，经由函数发生器的USB接口导入函数发生器。功率放大器选用AG1012型功率放大器，其作用是将函数发生器输出的电平信号放大到驱动换能振动系统工作所需功率。示波器选用TDS3012B型数字荧光示波器，其作用是监视和分析电信号。图2为实验方框图。

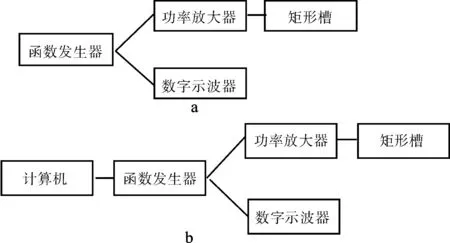
图2 正弦信号(a)和合成信号(b)激励实验方框图Fig.2 The block diagram under the incentive of the sine signal(a) and composite signals(b)

3 实验方法

向槽中加入一定浓度的亚甲基蓝水溶液，同时将铜版纸按一定方式浸入并固定在液体中，在超声场作用下，染料将优先附着在声能量较强处。这样，经过声场短时间辐照后，在铜版纸上就可以得到代表声场空间分布的染料图案[16]。

实验时亚甲基蓝水溶液液面高度为120 mm。先将铜版纸沿竖直或水平方向浸入液体，竖直放置时，纸下端紧挨槽底，水平放置时纸面距槽底40 mm。然后启动激励信号(正弦信号或合成信号)，系统工作20 s后取出铜版纸，晾干整平，即可获得不同信号激励下竖直和水平方向的声场分布。最后用扫描仪扫描染色后的图案以供分析。

4 实验结果分析

实验中功率放大器的输出功率约310 W，施加给换能振动系统的有载功率分别约240、250、270 W。实验结果如图3—10，所示图像均是由槽底部向液面上的声场分布情况按比例缩放的结果。

4.1 声源频率对声场分布的影响

图3—4是正弦信号激励下，不同频率的矩形槽超声振动系统空间声场分布情况。从图3看出，在单频正弦信号激励下，由于声波的相干性，竖直方向上声压及声能量密度都会出现极大、极小值的起伏变化，声场呈近似带状分布。如果取液体中的声速c=1 480 m/s，用公式λ=c/f计算3种谐振频率下的波长分别为62、41、26 mm，可见声源频率越高，波长越短，带状变得不明显，声场逐渐均匀。3种频率下的声波在矩形有界空间中传播时，激起简正波的个数由(4)式计算分别为113、389、1 531，可见随着频率的增加，空间简正波数目增加得更明显，大量的简正振动方式叠加“平均”掉空间声场的驻波效应，这是声场分布趋向均匀的另一个方面。由图4可知，水平方向声场分布随声源频率变化趋势与竖直方向相同，在整个平面内呈现起伏变化，即随着声源频率的增加，声场逐渐趋于均匀。

图3 正弦信号激励下的竖直方向上的声场分布Fig.3 The acoustic field distribution on the vertical direction under the incentive of sine signal

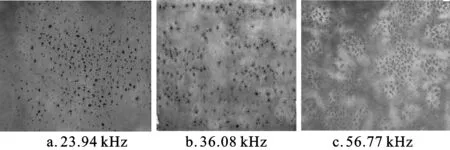
图4 正弦信号激励下的水平方向上的声场分布Fig.4 The acoustic field distribution on the horizontal direction under the incentive of sine signal

可见单频信号激励时，不论是竖直还是水平方向，有界空间中的声场分布都是随着声源频率的增加而趋于均匀，这一结果与上述理论分析结论一致。所以，从改善有界空间的声场均匀性的角度而言，高频信号激励优于低频信号激励。

4.2 不同合成信号对声场分布的影响

图5—10为不同合成信号激励时的声场分布情况。与对应的单频正弦信号激励相比，3种超声振动系统声场分布的均匀性都有明显改善。究其原因，一方面是多频信号的不相干性，使声场中的声压及能量密度的空间不均匀度变小；另一方面，对每种超声振动系统，合成信号激励实际上是有较高频率的信号参与激励换能器工作，相当于增加了声场中的简正声波数目。

图5 带宽为1 kHz的合成信号竖直方向上的声场分布Fig.5 The acoustic field distribution on the vertical direction under the composite signals of 1 kHz bandwidth

图6 带宽为1 kHz的合成信号水平方向上的声场分布Fig.6 The acoustic field distribution on the horizontal direction under the composite signals of 1 kHz bandwidth

图7 带宽为2 kHz的合成信号竖直方向上的声场分布Fig.7 The acoustic field distribution on the vertical direction under the composite signals of 2 kHz bandwidth

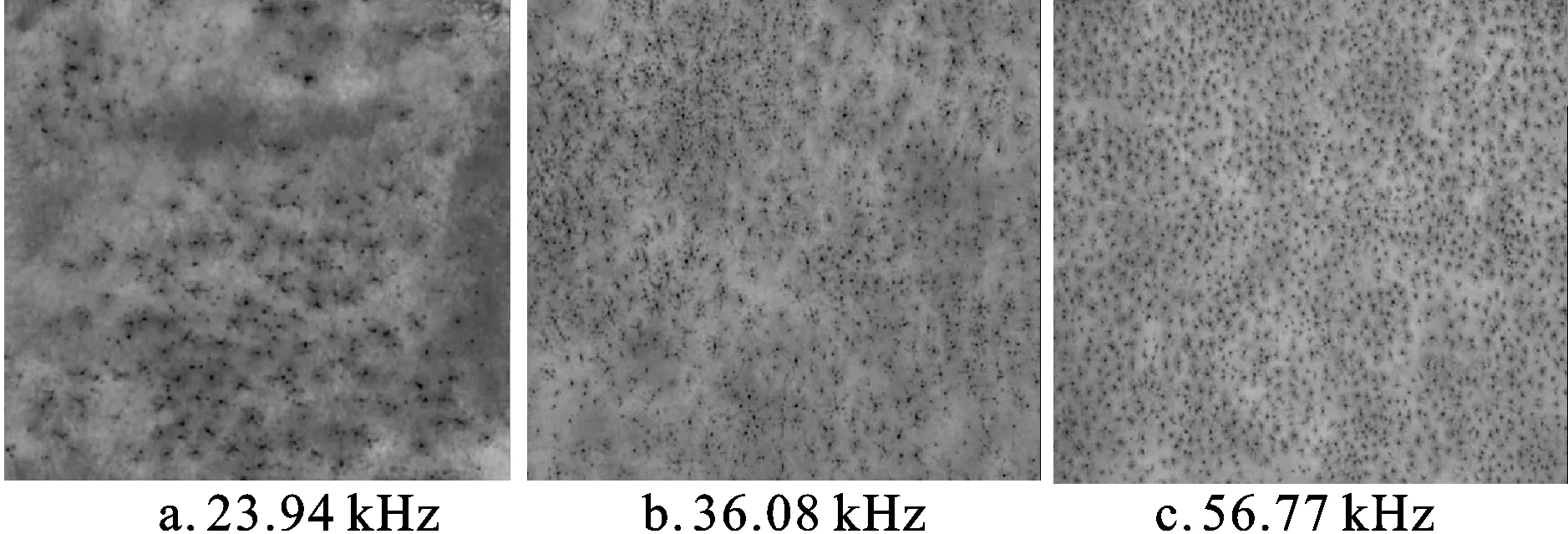
图8 带宽为2 kHz的合成信号水平方向上的声场分布Fig.8 The acoustic field distribution on the horizontal direction under the composite signals of 2 kHz bandwidth

图9 带宽为3 kHz的合成信号竖直方向上的声场分布Fig.9 The acoustic field distribution on the vertical direction under the composite signals of 3 kHz bandwidth

图10 带宽为3 kHz的合成信号水平方向上的声场分布Fig.10 The acoustic field distribution on the horizontal direction under the composite signals of 3 kHz bandwidth

但分析图5—10可知，合成信号在带宽Δf=1 kHz和Δf=2 kHz时，对声场均匀性的改善基本相同。Δf=3 kHz时，虽然对声场均匀性也有较明显的改善，但效果相对较差；且频率越低，这一现象越显著。这是由于超声换能振动系统的谐振特性，频带较窄时，合成信号的频率成分都在谐振频率附近，换能器的输出声信号幅度几乎相同，其叠加效果与上述理论分析结论基本一致。频带较宽时，由于激励信号能量分布在较宽的频率范围，换能器的输出声信号幅度相差较大，对应于偏离谐振频率较远的激励频率成分，换能器的输出声信号幅度很小，对声场分布的影响几乎可以忽略，其叠加效果以谐振频率附近的信号为主。这表明合成信号的带宽应结合具体换能系统的谐振特性综合考虑。

总之，在合成信号产生的多频声场中，由于声波之间的不相干性，声场的均匀性较单频有明显改善。对于不同频率的超声振动系统，Δf并非越宽越好，应根据系统的谐振特性选取合理的合成信号带宽。

5 结论

本文以矩形槽式超声振动系统为例，研究了不同激励方式对有界空间超声场分布的影响，从改善声场均匀性角度而言，理论分析和实验结果表明：

(1) 单频信号激励时，56.77 kHz优于36.08 kHz优于23.94 kHz，即声源频率越高，声场分布越均匀。

(2) 一定带宽下的多频合成信号激励时，从长时间平均效果来看，由于声波之间的不相干性，相比单频信号而言，声场均匀性都有明显的改善。

(3) 合成信号激励时，23.94、36.08及56.77 kHz 3种频率的结果与单频激励相似，即超声换能振动系统的谐振频率越高，合成信号激励对声场均匀性的改善越明显。

(4) 实验中，不同谐振频率的系统均采用相同带宽的合成信号。Δf=1 kHz和Δf=2 kHz时，对声场均匀性的改善基本相同；Δf=3 kHz时，虽然对声场均匀性也有较明显的改善，但效果相对较差，且频率越低，这一现象越显著。也就是说，Δf并非越宽越好，应根据换能振动系统的谐振特性，选取合适的带宽。

[1] 张明铎，任金莲，牛勇.侧面辐射声化学反应器的声场研究[J].西北大学学报:自然科学版，2009,39(6)：940-943.

[2] 魏鑫，吴胜举，许昊，等.槽壁边界对超声清洗声场特性的影响[J].陕西师范大学学报：自然科学版，2012,40(3)：42-45.

[3] 李娟，张明铎，马奭文.矩形声化学反应器空化场分布的研究[J].化学工程，2012，40(11)：52-55.

[4] 沈壮志，尚志远.用声波扩散改善清洗场中小功率声场的均匀性[J].应用声学，1999,189(5):41-43.

[5] 任金莲，张明铎，牛勇.改善大功率超声清洗声场均匀性的一种方法[J].压电与声光,2003,25(4):347-350.

[6] 梁召峰，周光平，莫喜平.换能器布阵数量对超声清洗声场特性的影响[J].压电与声光,2009，31(5):760-762.

[7] Jiang Leimeng,Verhaagen B,Versluis M,et al.The influence of ultrasonic intensity on the cleaning efficacy of passive ultrasonic irrigation[J].Journal of Endodontics,2011,37(5):688-692.

[8] 刘丽艳，闻精精，杨洋，等.固体颗粒对超声空化场的影响[J].化学工业与工程，2013,30(1):59-66.

[9] 林书玉，张福成.关于改善超声清洗声场均匀性的研究[J].应用声学，1992,12(2):34-38.

[10] 蒋建国，杨世辉，张群芳.槽式双频超声波发生器改善污泥脱水性能研究[J].应用基础与工程科学学报,2009,17(6):852-858.

[11] 任金莲，牛勇，张明铎.复频超声波清洗器的研制[J].压电与声光,2006,28(3):305-307.

[12] 姚文苇.复频声场的研究[J].陕西师范大学学报:自然科学版,2008,36(s1):20-22.

[13] 严勇文，隆志力，何将三.变频式超声波发生器的高速锁相研究[J].电子与封装,2010,10(2):35-39.

[14] 任金莲，牛勇，张明铎.复合频率超声波清洗声场均匀性研究[J].声学学报，2003,23(2):127-129.

[15] 杜功焕，朱哲民，龚秀芬.声学基础[M].南京：南京大学出版社,2010: 226-230.

[16] 方启平, 颜忠余, 黄金兰,等. 用染色法记录液体中大功率超声场的分布[J]. 声学技术, 1996，15(4):177-179.

〔责任编辑 李 博〕

The effect of different incentive methods on ultrasonic field distribution in bounded space

YAN Jing, ZHU Feifei, ZHANG Mingduo*, ZHENG Baoning, LI Yangyang

(School of Physics and Information Technology, Shaanxi Normal University,Shaanxi Key Laboratory of Ultrasonics, Xi′an 710119, Shaanxi, China)

Based on the sound wave superposition principle, the acoustic field distribution in a rectangular space is analyzed. The ultrasonic field distributions are experimentally studied under different incentives.It can be found that under single frequency sine signal, the sound field induced by higher frequency sound source distribute more uniformity.Because of incoherence among sound waves, the sound field uniformities under synthetic signals are observably improved than the single frequency signal.Further more the uniformity of sound field is obviously improved as the increasing of frequency.The results indicate that the bandwidths of synthetic signals should be choose to gain more uniformity sound field.Key words: single frequency signal; synthetic signal; ultrasonic field distribution; uniformity

1672-4291(2015)04-0039-04

10.15983/j.cnki.jsnu.2015.04.243

2014-07-30

国家自然科学基金(10574086)；陕西省教育厅科学研究计划(05JK165)

闫晶，女，硕士研究生，研究方向为功率超声。E-mail:1030996284@qq.com

*通信作者：张明铎，男，副研究员。E-mail:zmduo@snnu.edu.cn.

O426.2

A