Slab模型寻找表面态方法＊

陈建勇

（桂林航天工业学院理学部 广西 桂 林 541004）

王 星

（桂林理工大学博文管理学院 广西 桂 林 541006）

表面态存在于靠近表面的数层原子内.表面态的研究对于表面吸附、材料输运，以及拓扑绝缘体［1］等方面是非常有价值的.表面态的寻找可以通过构造半无限大体系来求解［2］，也可以构造有限厚度薄膜体系通过求解Slab模型的能带结构直接得到，我们假定薄膜的x方向为有限厚度d0，y和z方向无限延伸.方法如下.

以尖晶石结构的铁磁CdCr2Se4为例，当磁矩的方向是（001）时，CdCr2Se4具有 D4h对称性，以

为基，其八带Kane模型［3］的哈密顿量可以写成如下形式

参数通过与第一性原理计算的能带拟合得到，其中k＝k±ik，P＝，选基函数为

±xy

开放边界条件要求

式中x方向为有限厚度，厚度d0选取原则是薄膜要足够厚以保证中间的原子保持周期性体态的性质且两边的表面态不会通过薄膜产生相互作用.比如Bi2Se3表面态电子的是空间分布厚度约为30，即一个晶胞的厚度28.64［4］；晶体GaAs表面态的穿透深度随外加流体静力学压力增大而减小，压力为零时最大穿透深度为1.6，小于GaAs的晶格常数5.65［5］，且对于有量子霍尔效应的体系，其霍尔电导率等性质跟计算的薄膜厚度相关［6］.不同体系厚度的最终确定还是需要通过计算测试获得，增大d0做重复计算直到计算结果不再变化.此时kx不再为好量子数，得

展开

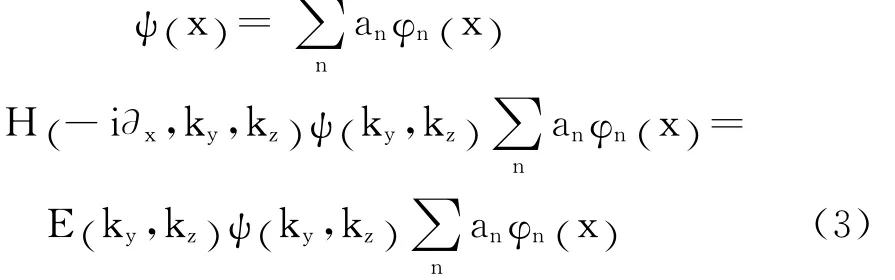
ψ（ ky，kz）为列向量，左乘ψ（ky，kz）φn′（x），利用｛ψ（ky，kz）｝的归一化性质，得到

将CdCr2Se4的八带Kane模型哈密顿量分解为H＝ H0（k）＋H1，其中 H1与k无关，有

其中εi（kx）＝，mi∥为平行方向有效质量.若kz＝kz0则H （kz）可移入H1，记为H′1，形成二维结构，久期方程

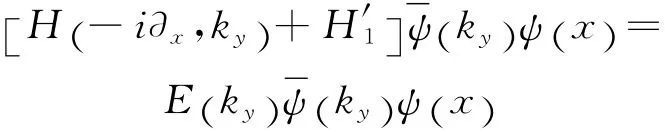
用 ｛φn＝sin｝展开ψ（x）得到新的H′new和H″new

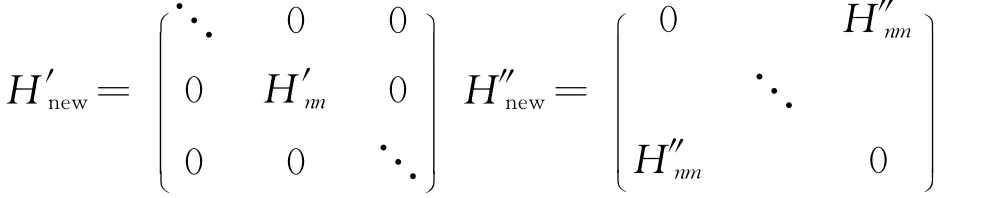
其中n为基函数标记，取值越大计算结果越精确同时计算量会增长很快，考虑计算的实现，需要取适当截断，例如n＝200，其中

另外所有与kx无关的项只有H′nn有非零值.这样的8n×8n哈密顿矩阵对角化便得到有限厚度薄膜的所有能量色散关系，与体态的能带对比便可以寻找是否存在表面态并可分析其成因.

1 Z.Hasan and C.L.Kane，Rev.Mod.Phys.82，3045，2010

2 M.P.LopezSancho，JournalofPhysicsF：MetalPhysics，15：851～858，1985

3 Lok C.Lew Yan Voon and Morten Willatzen《The k·p M ethod：ElectronicPropertiesofSemiconductors》USA，57～60，2009

4 张海军.固体中Wannier函数的计算及其应用：［博士学位论文］.北京：中国科学院，2009

5 闫祖威，班士良，梁希侠.压力下半导体GaAs的电子表面态.内蒙古大学学报（自然科学版），2001，32（6）

6 Gang Xu，Hongming Weng，Zhijun Wang，et al Phys.Rev.Lett 107，186806 2011