物理教学中培养学生创新思维方法探索*——《物理教育中培养学生创新素养》子课题研究概要
2016-01-12黄国龙
物理教学中培养学生创新思维方法探索*
——《物理教育中培养学生创新素养》子课题研究概要
黄国龙
(镇海中学浙江 宁波315200)
*宁波市“十二五”教育规划重点课题“物理教育培养学生创新素养探索”的研究成果之一,编号:YZD12021
摘 要:本文首先揭示现行中学物理教学中创新思维培养存在的问题和不足;其次根据创新思维的一般特性和中学物理教学的实际,确定中学物理创新思维方法培养的内容;最后,介绍有效培养学生创新思维方法的一些具体做法.
关键词:物理教学创新教育创新思维
作者简介:黄国龙(1964-),男,特级教师,主要从事中学物理教学及研究.
收稿日期:(2014-12-22)
1问题的提出
现行中学物理教学中,虽然学生创新思维方法培养的途径和策略较多,但存在如下问题和不足.
(1)注重必修课程中封闭性的创新思维教学,缺乏在开放性选修课程中深层次地实施创新思维培养
传统物理教学中较多局限于物理必修课程中实施创新思维培养,物理创新思维培养内容和策略比较零乱,缺乏系统性.由于探究时空限制引起创新活动缺乏深刻性、自主性、体验性,从而使创新思维培养策略缺乏课程化和深刻性.因而需要通过开发实施高水平的物理创新思维培养选修课程和研究性课题研究来促使创新思维活动的开放性,从而使物理创新思维培养深度化.
(2)物理竞赛教学功利化和应试化,缺乏有效培养学生创新思维
高中物理竞赛是培养创新思维的重要途径,然而,近几年高中物理竞赛教学中存在如下问题.
竞赛目的急功近利.学校、教师和学生把获奖能保送、加分做为竞赛目的.参赛学生缺乏对物理的一种内在兴趣和热情,缺乏对学习物理持续的动力,更缺乏对物理的专业抱负和志趣.
竞赛教学高度应试化.现在物理竞赛资料繁多,复杂、超纲、偏难题目较大,使物理竞赛成为高度应试化的活动,缺乏对学生进行创新思维的培养,严重偏离物理竞赛的原先宗旨.
(3)学教方式传统化,缺乏创新思维培养需要创新的学习方式和教学方式
创新思维培养需要有创新的学习方式和教学方式.然而,传统物理创新教学中缺乏创新学习方式和教学方式,缺乏类似科学探究背景中创新思维方法的展现和发挥过程,从而使创新思维方法培养停留在形式上,学生对创新思维方法没有得到内化.
2中学物理教学中创新思维方法培养内容
课题组根据创新思维一般性结合中学物理教学特殊性,整合中学物理竞赛教学,在整合一般性创新思维基础上,确定中学物理教学中创新思维方法培养体内容.
2.1一般性创新思维方法培养内容
(1)发散思维方法.能通过观念、知识、方法和技术等信息的重新组合,多角度地发散思维来审视研究问题,创新提出和解决问题.
(2)直觉思维方法.能运用思辨思维、想象思维、联想思维、灵感思维提出问题、分析解决问题.
(3)侧向思维方法.能从横向视角另辟蹊径提出、分析和解决问题.
(4)逆向思维方法.能从与已有思路的反方向去思考问题,创新解决问题.
2.2 物理创新思维方法培养内容
(1)等效思维方法.能根据等效关系把复杂、陌生问题转化为简单、熟悉问题,创新提出探究问题和解决问题.
(2)类比思维方法.能运用已有的知识、方法将新的复杂问题与熟悉简单问题或其他相似事物进行类比,从而创新地提出探究问题和解决新的复杂问题.
(3)移植构建思维方法.能移植应用熟悉领域的相关知识和方法构建熟悉、简单物理模型解答陌生领域复杂的物理问题,使复杂问题得到创新解答.
(4)对称思维方法.能根据物质世界对称性,运用时空、物理本质对称性创新提出问题,创新解答疑难物理问题.
(5)一般化思维方法.针对特殊问题、模型、理论在解答新的问题时遇到的困难,能从更一般的角度构建模型、提出理论、运用方法,创新解答新的问题.
(6)整体思维方法.能从系统、整体的角度综合分析多体相互作用、多过程运动、不同运动形式转化等问题,使复杂问题得到创新解答.
(7)特殊化思维方法.针对运用原有理论和方法解答问题所得的一般性结果,能从特殊的角度进行推理,对特殊推理结果进行评价,来揭示原有理论和方法存在问题.
3中学物理教学中培养学生创新思维方法探索
3.1整合物理竞赛教学活动科学系统开发实施物理创新思维方法培养课程
课题组重组原有物理竞赛社团活动,整合物理创新思维培养,科学开发《物理创新思维方法》课程,主要章节内容和课时安排如表1所示.综合运用“物理知识创新教学模式”、“物理方法创新教学模式”、“学术研讨式”、“辩论式”、“探究式”等创新的自主学习方式来实施创新思维方法课程.

表1 物理创新思维方法培养表

续表
案例分析1:运用等效、一般化、类比等思维方法创新降解求解物理竞赛“微积分问题”.
【例1】如图1所示,质量为m,带电荷量为Q的粒子放在离无限大导电板d处.现释放该粒子,求它经过多长时间到达板上.不计粒子重力.
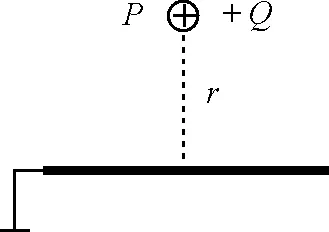
图1
常规解法:本题的常规解法是运用镜像法等效构建镜像电荷-Q,根据库仑定律和牛顿第二定律列出
电荷位移x满足dr=-dx,结合
得

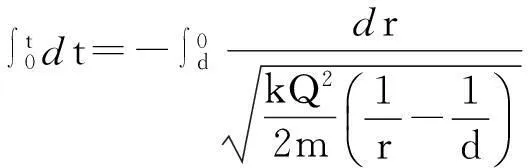
创新解法:教师引导学生综合运用等效、一般化、类比等思维方法创新解答这个问题.
运用等效思维方法构建镜像电荷模型:根据电势等效方法构建镜像电荷Q′,得

图2
把运动镜像电荷-Q等效为处于导体板上O点固定不动点电荷Q″(图2),根据
得
运用一般化思维方法构建一般模型:点电荷在电荷Q″作用下做直线运动,电荷Q受到电场力为
因而可以把点电荷运动近似为很扁的椭圆运动,长半轴
运用类比思维方法简化推理过程:此运动模型与天体运动模型相似,运用类比思维方法得
扁椭圆运动的运动周期为
电荷到达板所需时间等于半个运行周期
综合解得
由上分析可知,通过综合运用等效、一般化、类比等思维方法,创新降解解答这个疑难物理竞赛问题.
3.2构建实施“方法创新探究模式”培养学生物理创新思维方法
课题组根据方法创新特点整合物理竞赛教学,构建方法创新探究模式,有效地培养学生物理创新思维方法.

图3
物理方法创新探究模式流程如图3所示,特点是:以学生认知中原有方法为基础,以新的问题情景为切入点,以探究解答为动力,以方法求真探索创新和臻美创新为核心,以构建新的方法结构、培养学生创新思维方法为目标.学生原有方法包括思维方法,所创设新问题情境应能揭示原有方法的局限性,同时隐含了新的思维方法;当学生探究失败时,教师应引导学生进行求真探究(探究新的正确方法);当学生探究成功时,教师应引导学生进行臻美创新(寻求更简洁、更一般的方法).
案例分析2:运用方法创新探究模式探究“电荷分布规律”.
创设新的问题

图4
【例2】如图4所示,在电场强度为E的匀强电场中放置一个均匀金属球,其半径为R,由于静电感应,在球上产生了面电荷,面电荷密度为σ,试探究σ和图中标出的θ角的关系式.
学生错解:虚设球内的匀强电场由如图5(a)所示的两个无限大均匀带电(面电荷密度为σ0)平板产生的,两平板刚好与球相切.由于球内电场强度为零,因而一个平板与半球面电荷在球心O产生的电场强度大小相等.在球面上任取一微元Δs1,此微元在左面平板上相对应的微元为Δs2[如图5(b)所示].两微元在球心产生电场强度分别为
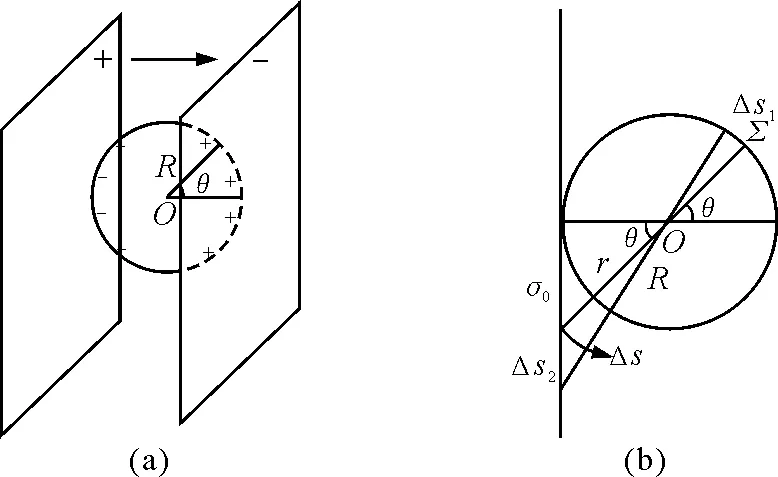
图5
根据如图5(b)所示的几何关系得
Δs1=R2ΔθΔφΔs2=r2ΔθΔφ
结合ΔE1=ΔE2,E=2πkδ0,得
导致悖论,揭示错误:针对这个解答,有些学生运用特殊化方法导致悖论:即令θ=90°时,推得δ→∞,这显然与事实(θ=90°位置δ应最小)矛盾.这个悖论揭示学生原有解答是错误的.
创新解答1:部分学生通过等效构建“双球电荷”模型解答这个问题:
如图6(a)所示,电荷密度分别为ρ和-ρ的两个半径都为R均匀带电球体球心的距离为d(d≪R),重叠部分电荷为零.取表面积为ΔS,高为dcosθ的小长方体微元,其带电荷量为Δq=ρΔSdcosθ,当d→0时,这些电荷只分布在ΔS表面上,电荷面密度为σ=ρ dcosθ.由如6(b)图可知,“双球电荷”模型在重叠处产生水平向右的匀强电场E,只要E-E0=0,则本题中金属球表面上电荷分布与“双球电荷”模型不重叠处表面的电荷分布等效,也为σ=ρ dcosθ.由电场叠加原理得双球电荷在球内任一点P产生的场强大小为

图6
结合σ=ρ dcosθ解得
创新解答2:运用一般化、等效、移植等创新思维方法创新探究电荷分布规律.


图7


图8
运用移植思维方法简化推理过程.在R≪d条件下,在球面上和球面外激发电场时,可把两镜像电荷等效为偶极子.偶极子在球面上任意点P产生电场强度为
P点径向电场强度满足
Er+Ecosθ=4πkδ
即
结合
从而解答
在探究上述电荷分布规律过程中,学生的特殊化、一般化、等效、移植等多种创新思维方法得到充分发挥,创新地解答复杂静电问题,多种创新思维方法得到有效培养.
3.3实施“悖论”①*①这里的“悖论”是科学研究中悖论的引申(移植到物理教学中).探究教学 培养学生创新思维方法在科学“悖论”探究中科学家自觉地运用创新思维方法发现科学“悖论”,揭示原有理论隐含的客观矛盾;运用创新思维方法分析科学“悖论”产生的原因,为提出新的科学理论打下基础;运用创新思维方法探究“悖论”、消除“悖论”,提出新的物理理论.虽然中学生探究物理过程和科学家探究物理过程在目标和难度上是不同的,但某种意义上讲,学生探究物理知识过程与科学家探究物理学过程中运用思维方法具有相似性.中学物理教学中实施“悖论”探究教学对于学生探究物理知识和物理创新教学具有十分重要的价值,是培养学生创新思维方法一有效的途径.
物理“悖论”探究教学中创新思维方法培养思路是:创设一些适合学生认知水平且能够激发探究兴趣和创新思维的问题情境,引导学生经历发现“悖论”、探究“悖论”原因、解答“悖论”问题等“悖论”探究过程,内化相关物理创新思维方法,从而培养学生的创新思维方法.
案例分析3:在探究“潜艇功率”、“悖论”过程中培养学生的创新思维方法
问题情景:
【例3】潜艇下方有推进器,用绝缘材料制成的直线通道推进器构成,其原理示意图如图9所示.在直线通道内充满电阻率ρ1=0.2Ω·m的海水,通道中a×b×c=0.3m×0.4m×0.3m的空间内,存在匀强磁场B=6.4T,方向垂直通道侧面向外.磁场区域上、下方各有a×b=0.3m×0.4m的金属板M和N,当其与直流电源相连后,在两板之间的海水中产生大小恒为I=1.0×103A的电流.设电流只存在于磁场区域,海水密度ρ2=1.0×103kg/m3.当潜艇以恒定速度v0=30m/s前进时,海水在出口处相对于推进器的速度v=34m/s,试求一个管道所消耗的电功率大小.

图9
(1)在导致“悖论”过程中,培养学生创新思维方法
在导致“悖论”过程中,可运用对称创新思维方法、特殊情形推理、运动可逆性、多角度思维等方法导致“悖论”,培养创新思维方法.
错误解法:在地面参照系中,安倍力推动潜艇功率为 P电1=BIcv0,从管道右侧出来水相对地面的速度为
vd=vr-v0=4m/s
在Δt时间内有质量为m的水由静止加速到速度为vd.安倍力做功使水加速消耗电功率为满足
电阻上消耗的热功率为
解得
Pr=5×105WP电1=5.76×104W
P电2=3.84×103W
消耗总电功率为
P电=Pr+P电1+P电2=5.614 4×105W
运用对称思维方法导致“悖论”:部分学生运用相对性原理(事实上是对称创新思维方法一具体形式)导致“悖论”.以潜艇为参照系,电阻上消耗热功率还是
Pr=I2R=5×105W
水以v0=30m/s速度从潜艇左端进水口s1进入管道,以vr=34m/s速度从右端出水口s3流出,推动水加速消耗的电功率满足
m=ρs3vrΔt
解得
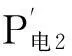
消耗总电功率为

根据相对性原理,消耗的电功率在不同参照系中应相同,但上述两种解法得出不同结果,导致“悖论”.这个“悖论”意味着上述解答存在问题.教师把探究上述错解原因及正确解法做为学生探究课题.
(2)在分析“悖论”原因过程中,培养学生创新思维方法
在分析“悖论”产生的原因过程中,可运用特殊化思维、一般化思维、发散思维等方法分析“悖论”原因,培养学生的创新思维方法.
特殊化思维分析错误原因:对于特殊情形(假若没有安倍力),潜艇管道向左运动,根据连续性原理(v1s1=v3s3)和图10可知v3>v1.原因是由于管道两端水对进入管道的水要做功,从而导致这部分水动能增加.在本问题中,由于安倍力和管道左右水对流入管道的水共同做功使这部分水动能增加.错解原因之一是认为安倍力做功所消耗的电能等于流进管道部分水的动能增量.
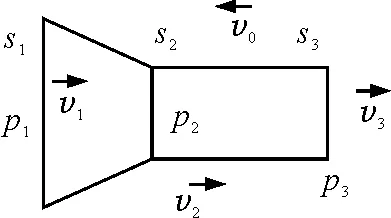
图10
(3)在探究解答“悖论”问题过程中,培养学生创新思维方法
在探究解答“悖论”问题过程中,可运用等效、类比、对称、一般化、移植模型等创新思维方法,创新解答物理问题,培养学生的创新思维方法.
运用发散思维,创新物理模型:从流体连续性角度分析,根据连续性原理v2s2=v3s3,由于长方体管道内横截面积相等,因而水在长方体管道内应做速度为vd=4m/s的匀速运动,而不是加速运动.安倍力做功消耗电功率即为安倍力对流进潜艇内水所做功功率和反作用力对潜艇做功功率之和,满足
P安=BIcv0+BIcvd
解得
P安=6.528×104W
消耗总的电功率为
P电=5.652 8×105W
运用对称创新思维方法,简化探究过程:部分学生运用对称思维方法(巧选潜艇参照系)探究解答:根据连续性原理,水在长方体管道内做速度为vr=34m/s的匀速运动,安倍力对流进管道内水所做功消耗的电功率为P安=BIcvr,解得
P安=6.528×104W
消耗总的电功率为
P电=5.652 8×105W
结果与地面参照系解答结果相同,符合相对性原理,大大简化解题过程.
参 考 文 献
1黄国龙,等.物理教育中培养学生创新素养探索课题研究概要.物理通报,2015(1):13~17
2王浩川,等.构建一般化电荷模型求解静电物理问题.物理通报,2014(6):72~74
3金旭统,等.对一道物理高考题错解分析及创新解答.物理通报,2014(10):91~93

