“近似法”在物理解题中的应用＊

刘俊娟

（河北师范大学附属民族学院 河北 石 家庄 050091）

魏增江

（石家庄理工职业学院 河北 石 家庄 050091）

“近似法”是在分析处理和研究某些物理现象和问题时，根据所研究问题的需要，忽略研究对象和问题的次要因素，突出其主要矛盾和本质特征，科学合理地对所研究问题进行近似处理的方法.使用近似方法需要对所研究的问题和近似条件有足够的了解和分析，并且能灵活应用所学知识.因此通过近似方法的应用，能检验我们掌握物理知识的深度、广度和灵活程度，能培养逻辑思维能力和应用物理知识分析、处理、解决实际问题的能力.可见，近似方法在物理学中占有相当重要的地位.

下面就力学中的问题来举例说明近似法的应用.

【例1】谐振动物体位在小区间的概率

一物体可视为质点沿x轴做振幅为A，圆频率为ω的谐振动.某人对此物体作随机观察，求此物体出现在微小区间0≤x≤a内的概率［1］.

解：用3种近似方法求解

方法一：几何图形近似方法

质点做谐振动的参考圆如图1所示，因a很小，故有如下近似关系：a＝Aθ，设物体经过区间a的时间为ta，因为一周期内物体两次经过区间a，所以出现在该区间的概率为

图1

方法二：函数关系近似方法

取x＝0，v＞0为计时起点，则物体振动方程为x＝Asinωt，当a很微小时，对应的ta及ωta也很微小，因而有如下近似关系

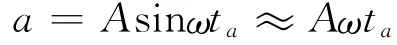
由此可得

所以有

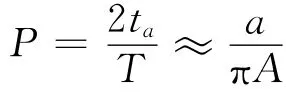
方法三：物理关系近似方法

根据能量守恒

可得物体振动的最大速度

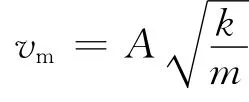
因为在0≤x≤a微小区间内物体振动加速度甚小，所以可以把物体在这区间内的运动近似当作“匀速”运动，因而有

所以

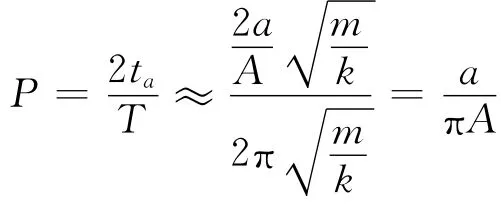
由以上3种方法可见，第一种用几何图形近似，直观形象；第二种用函数关系近似，格式严密；第三种从物理关系“匀速”近似处理，思路清晰，概念清楚.3种方法实质上都是把“变当作不变”处理，故实质和结果是一致的.但必须指出，上述近似方法可行，是因为在该区间内物体的加速度近似为零，否则不能近似.

【例2】运动学问题

有一个球体在某液体中竖直下落，球体的初速度v0＝10j（SI），它在液体中的加速度a＝－1.0vj（SI）.问：

（1）经多少时间后可以认为小球已经停止运动？

（2）此球体在停止运动前经历的路程有多长［2］？

解：由题意可得

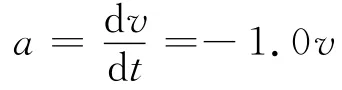
所以有

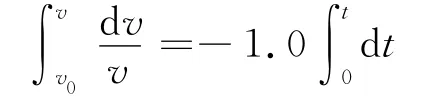
解得

可见，球体的速度v随时间t的增加而减小.又由速度的定义有

得

有

由式（1）可见，当v＝0时，时间t→∞.由式（2）可见，当t→∞时，y＝10m，这似乎有些不切合实际.为精确求解，可利用式（1），先求质点的速率v分别达到和时所经历的时间如表1所示.

表1 质点达到各速率经历时间

从表1可看出，在t＝6.9s和t＝9.2s时，球体已几乎不再运动，而所经历的路程已显示出其极限值10m了.故本题答案为：小球在运动几乎停止前运动了9.2s，经历的路程约为10m.这种近似处理的方法，不但简化了问题，而且准确.

【例3】匀质薄圆板与质点的引力势能

一半径为R，质量为M且质量均匀分布的薄圆板，在板的中垂线上有一质量为m的质点.若取无穷远为势能参考点，用类比方法求它们的引力势能，讨论质点距板极远和距板很近的情况［3］.

解：由类比方法可得质点与薄圆板相距为r时的引力势能为

当质点距圆板极远时，rR，应用二项式定理展开上式可得

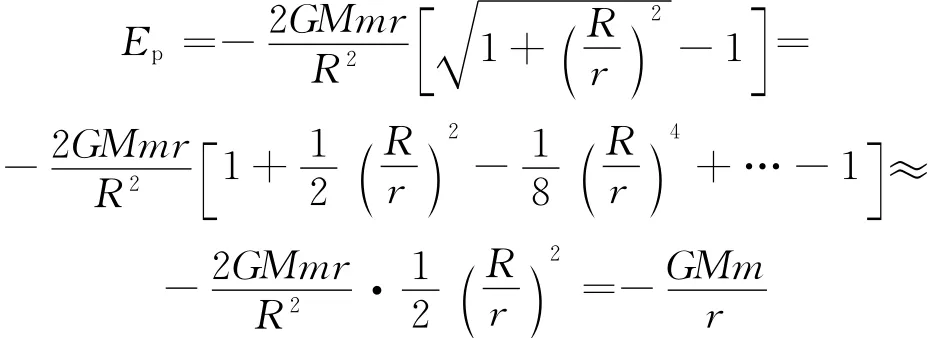
此式正是把圆板视为质点的结果.

当质点距板很近时，xR，圆板质量可视为面分布，可得

应该强调，在对引力势能做近似计算时，引力势能不能近似为零，也不能近似为常量.因为如果在某区域内引力势能为常量，那么在该区域内引力就为零，这是不合理的.在近似计算中，应该特别注意这一点.在对结果进行近似处理时，可以根据具体情况，结合数学知识，采用不同的近似方法.比如利用泰勒级数或傅里叶级数展开，可以求得许多函数的近似解；再比如用有限过程代替无限过程；或者忽略一些较小项对结果的影响，进行数量级的估算等.

从以上的例题中看出，近似法的使用，不但能简化物理问题，还可以抓住问题最本质的因素，建立正确的物理规律，得到最主要的科学依据.在建立物理模型、推导物理规律、处处渗透着近似处理的思想方法.可以说，善于对实际问题进行合理的近似处理，是学习的重要方法，也是科学素质和综合能力的体现.

1 康颖.大学物理（新版）第一版.北京：科学出版社，2005.133～136

2 周继芳.近似法在物理学中的应用.自然科学，2009（7）

3 马文尉.物理学习题分析与解答.北京：高等教育出版社，2004.103