正多面体的转动惯量＊

邱为钢

（湖州师范学院理学院 浙江 湖州 313000）

张 萍

（北京师范大学物理学系 北京 100875）

转动惯量的计算是大学物理教学中一类典型题目，文献［1～3］给出了椭圆环、圆锥、园台等物体的转动惯量.这些物体都具有圆柱对称性，那么，具有点群对称性的正多面体转动惯量怎么计算？文献［4］给出了5种正多面体的转动惯量，科学计算软件Mathematica 8.0多面体软件包PolyhedronData中的InertiaTensor指令也给出了各种多面体的转动惯量.正多面体可以由杆（线段）、面、体组成，或者说，质量分别均匀分布在顶点、棱、表面或体内，这种情况下，多面体的转动惯量如何表示？我们给出了杆、三角形和四面体转动惯量的顶点坐标表示［5］.由文献［4］的推论可知，正多面体的转动惯量最终表示与坐标轴的取向无关，与各点坐标方式表示无关，只与几何量有关.这样一来，就可以选取一个最容易计算的正多面体的顶点坐标表示，把正多面体剖分为点、线段、三角形和四面体，再组合起来，得到正多面体的转动惯量.

根据杆、三角形和四面体内点坐标的参数表示，由转动惯量的积分定义得到如下结论［5］，设杆的两个端点对应的向量为ri＝ （xi，yi，zi），i＝1，2，那么杆对z轴的转动惯量是

设三角形的3个顶点对应的向量为ri＝（xi，yi，zi），i＝1，2，3，则三角形板对z轴的转动惯量是

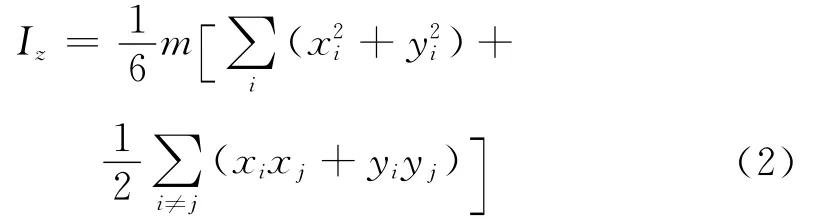
设四面体的4个顶点对应的向量为：ri＝ （xi，yi，zi），i＝1，2，3，4，则四面体对z轴的转动惯量是

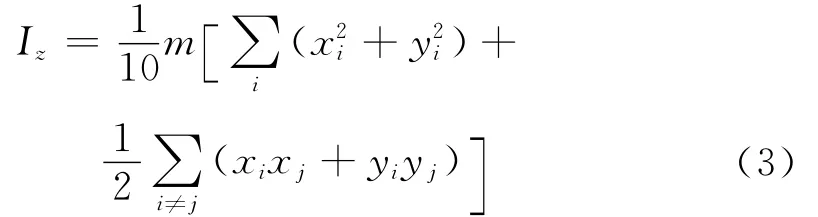
以上物体，对x，y轴的转动惯量，由指标x，y，z轮换得到.

表1 正多面体的顶点坐标

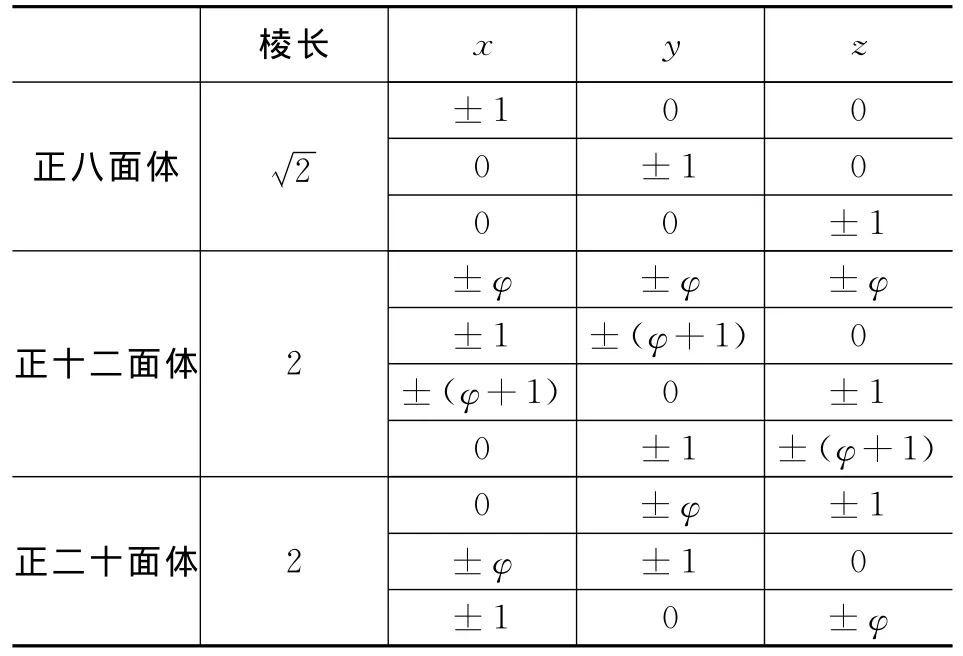
续表

由转动惯量的坐标表示（1 2 3 式以及表1给出的多面体顶点坐标，对多面体进行合理的剖分.计算得到质量分别均匀分布在多面体各个顶点，各条棱、各个面和体内的转动惯量，如表2所示.

表2最后一列的数据与Mathematica多面体软件包PolyhedronData中InertiaTensor指令和文献［4］给出的转动惯量完全一致.

与文献［4］所用的几何和积分方法相比，我们所用的坐标表示方法更加简明，而且容易编程计算.

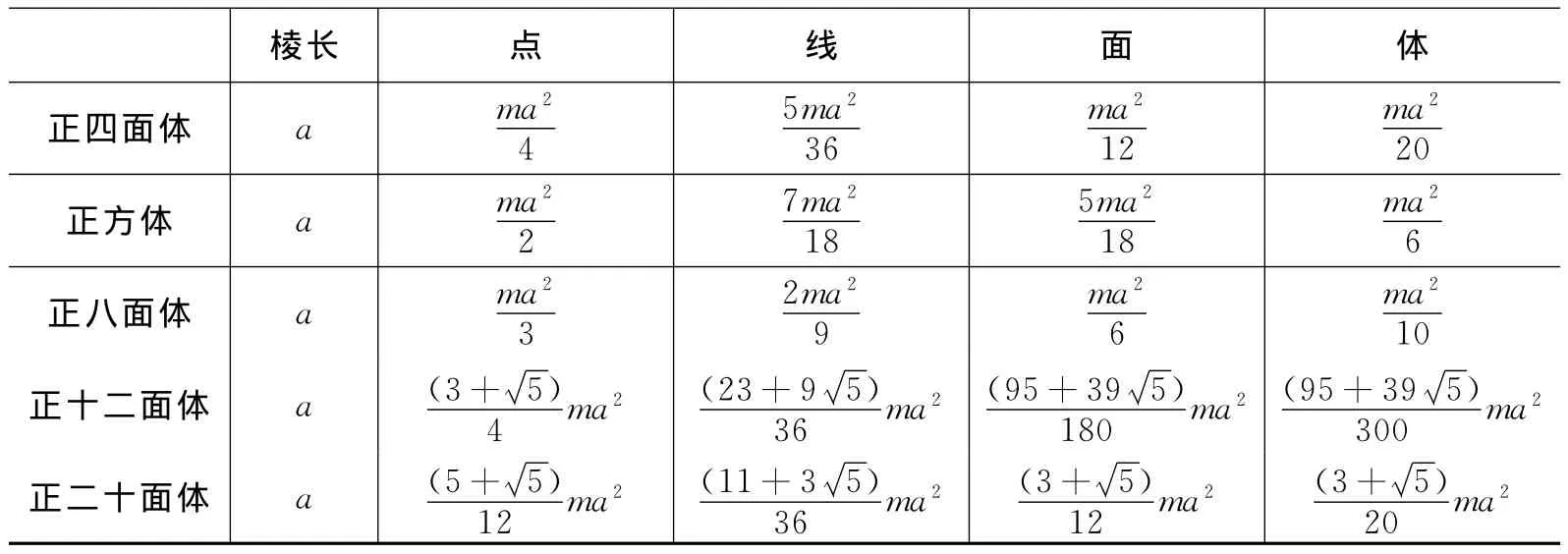
表2 正多面体的转动惯量

对于Mathematica多面体软件包Polyhedron－Data中其他多面体，有兴趣和时间的读者不妨用我们的方法算一算，这儿就不详细探究了.顺便说一下，Mathematica计算转动惯量用的是直接积分方法，借助了PolyhedronData中的RegionFunction选项和Boole函数.当然，实际物体不大可能呈现正多面体形状，这些物体的转动惯量张量的计算，可以沿用文献［5］的思路，三角形或四面体剖分，利用三角形或四面体转动惯量的坐标表示，直接求和计算，这大大简化了手工计算的难度.

1 赵新闻，周欣然，杨兵初.椭圆环刚体的转动惯量.大学物理，2008，27（6）：13～14

2 楼智美.巧算常见均质旋转体对母线的转动惯量.大学物理，2003，22（11）：26～27

3 楼智美.均质旋转面绕旋转轴转动的转动惯量.大学物理，2009，28（12）：22～24

4 刘甲刚，严云玲.均质正多面体主惯量轴和主矩.陕西工学院学报，1996，12（1）：78～83

5 邱为钢.转动惯量的坐标表示.物理通报，2014（2）：16～18