考虑两粗糙面分形特性的接触模型
2015-10-29陈立锋蔡志华谷金良
陈立锋 李 奇 蔡志华 谷金良
湖南科技大学,湘潭,411201
考虑两粗糙面分形特性的接触模型
陈立锋李奇蔡志华谷金良
湖南科技大学,湘潭,411201
基于M-B分形接触模型,通过构建接触系数建立了考虑两粗糙面分形特征的接触模型。分析结果表明,修正模型能较好地与实验数据相吻合,并适用于更大的载荷,修正模型综合考虑两粗糙面的特性,其计算结果与实际接触情况更相符,为摩擦磨损预测、磨粒分析以及不同粗糙度表面的接触分析提供了参考。
微凸体;两粗糙面;分形特征;接触
0 引言
自Mandelbrot[1]提出分形概念以来,由于分形理论在解决复杂非线性问题的特殊优势,分形理论在摩擦学、接触力学等领域得到广泛应用[2]。Majumdar等[3]通过W-M函数模拟粗糙表面的形貌特征,提出了尺寸独立的M-B接触模型,为分形理论在接触力学中的应用奠定了理论基础。Yan等[4]提出了三维分形表面的W-M函数生成方法,将分形接触模型推广至三维。Wang等[5]基于M-B模型将实际接触面积与微接触截面积进行区分,得到了M-B修正模型。Morag等[6]针对M-B模型的一些质疑进行研究,通过改进单个微凸体模型对M-B模型进行了修正。国内关于分形接触模型的研究也取得较好的成果,文献[7-8]通过考虑弹塑性变形,建立了考虑微凸体弹塑性变形的分形接触模型;文献[9-10]考虑粗糙表面的多重分型特性,建立了多重分形接触模型。分形接触模型也在材料磨损、润滑、接触刚度分析[11-13]等领域得到广泛研究。
以往的模型通常将两个粗糙面的接触视为一个光滑面和一个粗糙面的接触,模型得到简化的同时也存在以下不足:①以往的模型未考虑不同粗糙度的平面接触时的情形,当不同粗糙度的平面接触时,微凸体数量应以更粗糙的一面为准,特别是当两表面粗糙度相差较大时,简化处理将产生较大误差。②以往的模型忽略了不同大小的微凸体接触的情形,实际接触时应是不同大小的微凸体相接触,接触面积以较小微凸体为准,简化处理将导致分析得出的实际接触面积偏大。
接触面的接触性能应是由两粗糙面共同决定的,在接触强度分析时,考虑两粗糙面的表面特性是十分必要的。本文通过对分形理论的M-B模型进行修正,提出了两粗糙面接触系数的计算方法,并建立了不同粗糙度表面的接触模型,运用MATLAB进行仿真分析,研究了载荷、分形维数和分形特征尺度对接触性能的影响,最后,将结果与Bhushan[14]的实验数据进行对比,以验证修正模型的合理性。
1 M-B修正模型的建立
1.1M-B原始模型
M-B分形接触模型是微观上考虑接触表面形貌特征的有效模型[15],模型中将接触视为一个粗糙面和一个光滑平面的接触,假设粗糙表面由W-M函数来定义,微凸体变形状态与其接触面积相关,结合Mandelbrot[16]关于“岛屿面积分布理论”的研究,提出了尺寸独立的M-B接触模型。
如图1所示,粗糙面与光滑面发生接触,微凸体数满足“岛屿面积分布理论”[16],得到微凸体面积与数量的关系,微凸体面积分布函数为
(1)
式中,a为微凸体面积,m2;al为最大微凸体面积;D为分形维数。

图1 粗糙面与光滑面的接触
粗糙面接触时,不同大小的微凸体以ac为临界面积发生弹性变形和塑性变形,单个微凸体接触面积和弹性载荷Pe(a)、塑性载荷Pp(a)的关系为
(2)
Pp(a)=Kσya
(3)
式中,E为综合弹性模量,Pa;G为特征尺度,m;σy为材料屈服强度,Pa。
模型假设在一定载荷下,微凸体数量不变,面积随载荷增加而变大,部分微凸体接触由于接触面积变大而从塑性变形变为弹性变形。
综上所述,可得出总载荷与实际接触面积的关系。当最大微凸体面积al大于临界接触面积ac时,微凸体同时发生弹塑性变形:
(4)
式中,Km为与硬度相关的系数,通常取1.2;as为最小微凸体面积,通常取0。
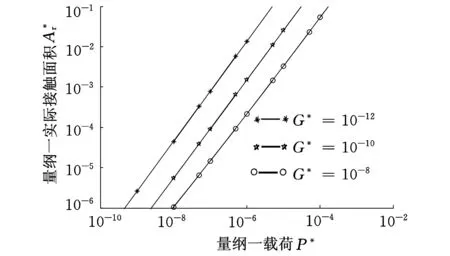
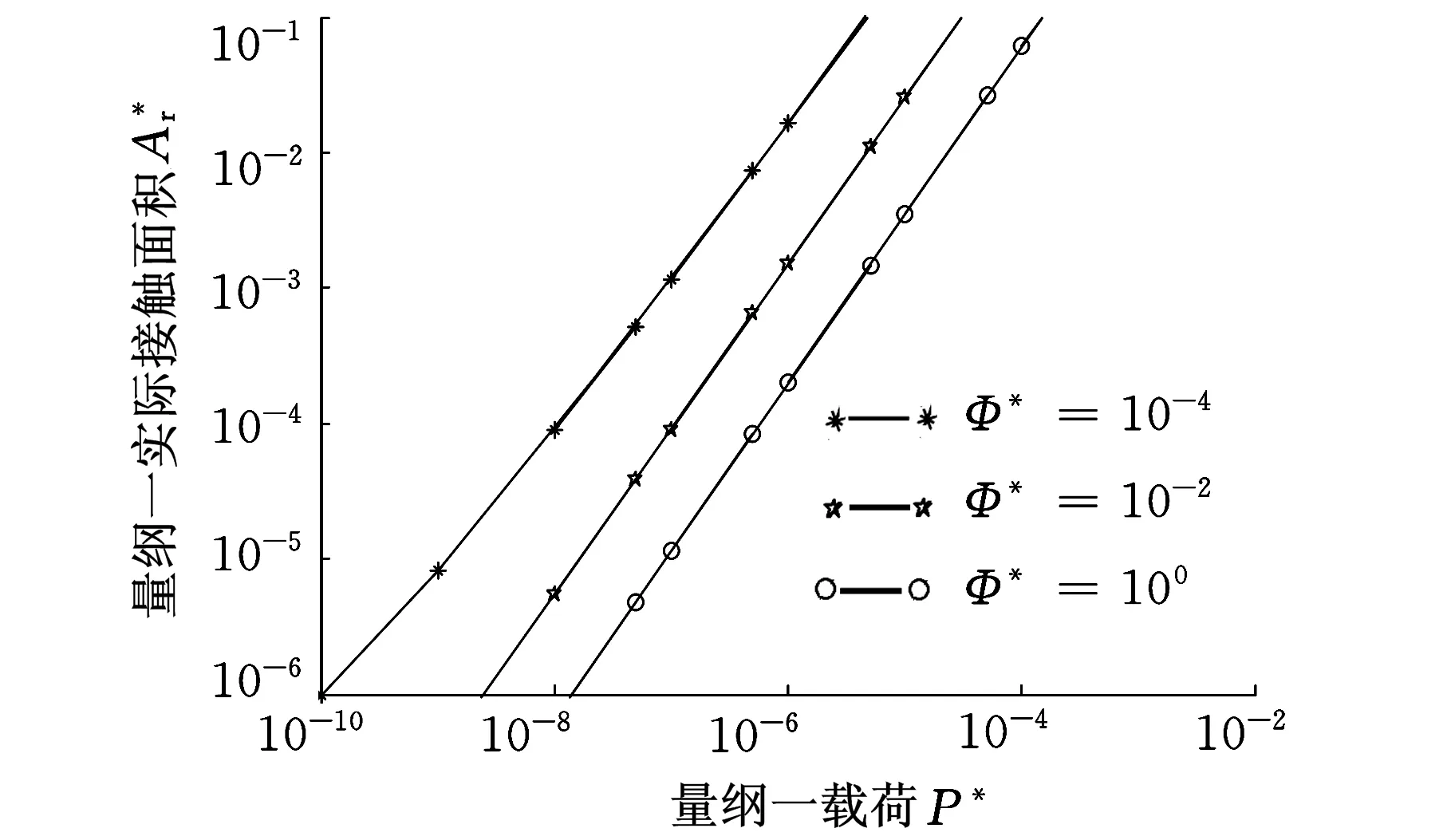
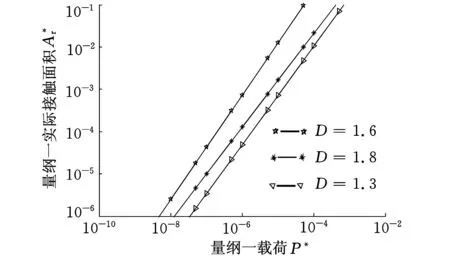
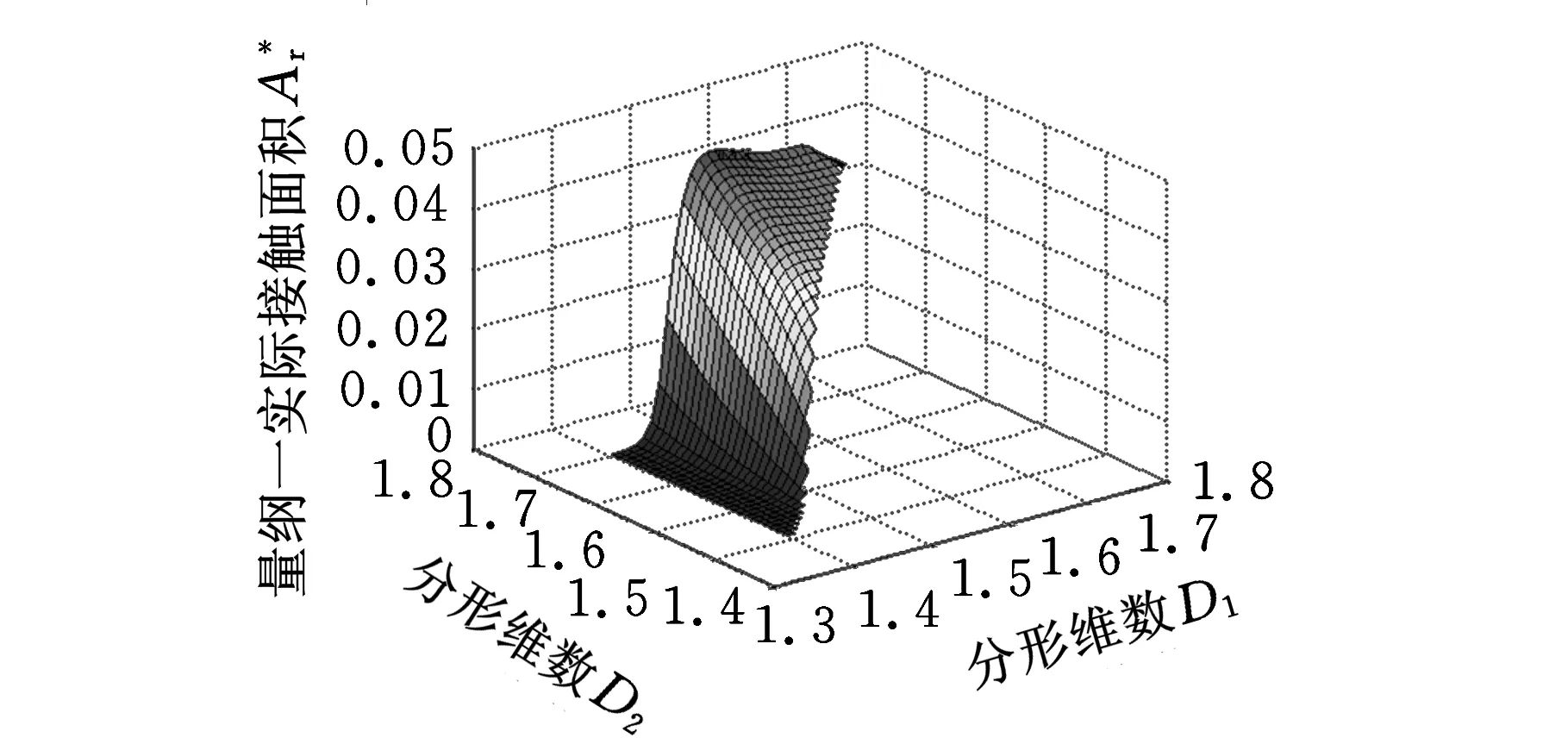
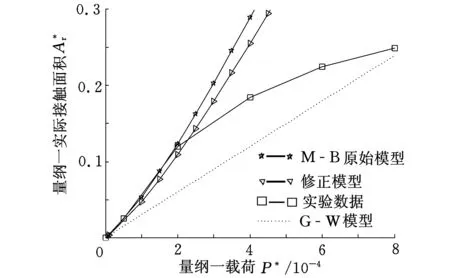
当al (5) 1.2M-B模型的修正 粗糙面之间的接触实质就是多个微凸体之间的接触,本文在M-B原始模型的基础上构建接触系数,得到同时考虑两粗糙面特性的分形接触模型。研究表明,多数粗糙表面的形貌特征满足正态分布[17],因此基于M-B模型提出一些假设,两粗糙面A与B发生接触,在一定载荷范围内,发生接触的微凸体数量保持不变,如图2所示,两粗糙面在受载后,微凸体分别发生弹塑性变形,两粗糙面之间存在一个接触面,本修正模型将粗糙面之间的接触视为两粗糙面以接触面为分界发生的接触,不同大小的微凸体之间随机接触,即粗糙面A和B分别与同一个接触面发生接触并满足“岛屿面积分布理论”,与接触面发生接触的微凸体数量保持不变,而两粗糙面之间不同大小的微凸体随机发生接触,不同大小的微凸体之间发生接触的概率与其在总面积中所占的比例成正比。忽略两粗糙面接触时,部分微凸体之间发生局部接触或不发生接触的情形,侧重于考虑不同大小微凸体的接触以及发生接触的微凸体总数变化。 图2 两粗糙面A、B之间的接触 1.2.1接触系数的建立 通过考虑两粗糙面接触时,两粗糙面上微凸体大小与数量对实际接触面积的影响来构建接触系数。如图2所示,假设两个面积相等的粗糙平面A、B相接触,面A较面B更为粗糙,单位面积内面A的微凸体数小于面B的微凸体数,即相同面积下,面A上的微凸体总数小于面B的微凸体数,则两平面接触时,发生接触的微凸体数n(a)应以较为粗糙的面A为准。即微凸体总数相对较少的面A决定发生接触的微凸体总数,发生接触的微凸体中面积为a的微凸体总数为 (6) 其中,D1为面A的分形维数,与M-B模型的假设相同[1],设面A与面B的最大微凸体面积al相同,最小微凸体面积as趋向于无穷小。 粗糙面接触时,微凸体之间随机发生接触且符合正态分布,不同大小的微凸体之间发生接触的概率与其在总面积中所占的比例成正比,由此构建接触系数。 假设面A上一组大小相同的微凸体,面积记为a,与面B上面积小于a的微凸体接触的概率为λ1,则 (7) 面A上微凸体中与面B上面积大于a的微凸体接触的概率λ2为 (8) 式中,D2为面B的分形维数;n(a)2为面B上面积为a的微凸体总数。 1.2.2修正模型的建立 两不同大小的微凸体相接触时,接触面积应以较小的微凸体为准,如图2所示,两粗糙面接触时,实际接触面积只需要考虑相对较小的微凸体,因此两粗糙面发生接触的微凸体可以分为两类,即相对较小的微凸体在面A时和较小的微凸体在面B时。 假设面A上一组大小相同的微凸体,面积记为a,接触时分为以下两种情形: (1)相对较小的微凸体在面A时。两个微凸体接触的面积应该由面A上的微凸体所决定,用于分析计算的参数以面A为准,即在此情形时模型的计算参数(分形维数、特征尺度、材料特性参数等)只受面A影响,面A上的相对较小的微凸体具有以下特性:①接触面积由面A上相对较小的微凸体所决定;②这一部分微凸体仍满足“岛屿面积分布理论”,面A上相对较小的微凸体数量为 n(a)A=n(a)λ2 (9) 当al>ac1(ac1为面A的临界接触面积)时,面A上载荷与实际接触面的关系为 (10) 式中,E1、G1、σy1分别为面A的弹性模量、特征尺度、极限屈服强度。 当al (11) (2)相对较小的微凸体在面B时。分析计算的参数应以面B为准,面B上发生接触的微凸体具有以下特性:①接触面积由面B上相对较小的微凸体所决定;②微凸体在面B上随机分布,仍服从正态分布,即面A上的微凸体与面B上的微凸体随机发生接触,设面A上一组面积为a的微凸体,在情形2时,面B上与其接触的微凸体面积在0~a之间,面B上发生接触的微凸体面积取近似值a/2,面B上相对较小的微凸体数量为 n(a)B=n(a)λ1 (12) 当al>ac2(ac2为面B的临界接触面积)时,面B上载荷与实际接触面的关系为 (13) 当al (14) 关于总载荷P与实际接触面积Ar的关系,列出修正模型的主要情形如下: 当al>ac1,al>ac2,D1≠1.5且5-2D2-D1≠0时,有 (15) 实际接触面积为 (16) 弹性接触面积为 (17) 塑性接触面积为 (18) (19) 图3 不同载荷下G*对的影响 图4 不同载荷下Φ对的影响 图5 不同载荷下D对的影响 图6 不同载荷P*下的最优分形维数D 图7 D1、D2与的关系 图8 D1、D2与的关系 根据文献[3,14]所测得的数据,M-B模型中材料特性参数Φ=0.05,量纲一特征尺度系数G*=10-10,分形维数D=1.38。假设修正模型中两表面材料相同,分形维数和特征尺度相等,代入以上数据分别与M-B原始模型、实验数据、G-W模型[21]对比,分析修正模型的合理性,图9所示为修正模型与实验数据对比分析结果。 图9 修正模型与实验数据、M-B原始模型、G-W模型对比分析 由图9可知,M-B原始模型在P*<2×10-4时与实验数据吻合较好,但在中载荷时开始出现偏差,而G-W模型仅在高载荷时与实验数据相吻合。本文提出的修正模型能适用于更大范围的载荷,在低载荷时与实验数据相差不大,中载荷时与实验数据更为吻合,而在高载荷时误差更小。由于在高载荷时,相邻的微凸体相互间的作用变大,而分形模型忽略了这一因素,故在高载荷时误差较大。 (1)本文研究了两粗糙面接触强度计算模型。该模型将粗糙面之间的接触视为多个微凸体之间的接触,基于分形理论考虑了不同大小微凸体的接触以及发生接触的微凸体总数变化,将发生接触的微凸体分为两大类,在M-B原始模型的基础上构建接触系数,得到同时考虑两粗糙面特性的分形接触模型。 (2)随着载荷的增加,实际接触面变大,特征尺度G与材料特性参数Φ越小,实际接触面积越大,并且存在一个分形维数值D使表面接触性能达到最优,该最优值受特征尺度G和材料特性参数Φ的共同影响。 (3)修正模型综合考虑两粗糙面的分形特性,其计算结果与实际接触情形更加吻合,为摩擦磨损预测、磨粒分析以及不同粗糙度表面接触分析提供了参考。 [1]Mandelbrot B.How Long is the Coast of Britain? Statistical Self-similarity and Fractional Dimension[J].Science (New York),1967,156(3775):636-638. [2]刘莹,胡敏,余桂英,等.分形理论及其应用[J].江西科学,2006,24(2):205-209. Liu Yin,Hu Min,Yu Guiying,et al.Fractal Theory and Its Applications [J].Jiangxi Science,2006,24(2): 205-209. [3]Majumdar A, Bhushan B.Fractal Model of Elastic-plastic Contact between Rough Surfaces[J].Journal of Tribology,1991,113(1):1-11. [4]Yan W,Komvopoulos K.Contact Analysis of Elastic-plastic Fractal Surfaces[J].Journal of Applied Physics,1998,84(7):3617-3624. [5]Wang S,Komvopoulos K.A Fractal Theory of the Interfacial Temperature Distribution in the Slow Sliding Regime:Part I—Elastic Contact and Heat Transfer Analysis[J].Journal of Tribology,1994,116(4):812-822. [6]Morag Y,Etsion I.Resolving the Contradiction of Asperities Plastic to Elastic Mode Transition in Current Contact Models of Fractal Rough Surfaces[J].Wear,2007,262(5):624-629. [7]董霖,张永相.M-B弹塑性接触模型的修正[J].四川工业学院学报,2001,20(2):4-7. Dong Lin,Zhang Yongxiang.The Modification of M-B Model for Elastic-plastic Contact between Rough Surfaces[J].Journal of Sichuan University of Science and Technology,2001,20(2):4-7. [8]缪小梅,黄筱调,袁鸿.考虑微凸体弹塑性变形的结合面分形接触模型[J].农业机械学报,2013,44(1):248-252. Miao Xiaomei,Huang Xiaodiao,Yuan Hong.Fractal Contact Model of Joint Interfaces Considering Elastic-plastic Deformation of Asperities[J].Transactions of the Chinese Society for Agricultural Machinery,2013,44(1):248-252. [9]孟凡明,赵荣珍,张忧云.多重分型表面的弹塑性接触模型研究[J].西安交通大学学报,2001,31(2):5-7. Meng Fanming,Zhao Rongzhen,Zhang Youyun.Multiple Points on the Surface of the Elastic-plastic Contact Model Study[J].Journal of Xi’an Jiaotong University,2001,31(2):5-7. [10]董雯,张永相.双重分形特征表面弹塑性接触模型的研究[J].润滑与密封,2003, 51(2):6-8. Dong Lin,Zhang Yongxiang.Research on Elastic-plastic Contact Model for Bifractal Surface[J].Lubrication Engineering,2003,51(2):6-8. [11]王乙潜,黄立萍.分形理论在材料磨损表面分析中的应用[J].材料导报,1998,12(2):8-10. Wang Yiqian,Huang Liping.Application of Fractal Theory in the Surface Analysis of Worn Material[J].Materials Review,1998,12(2):8-10. [12]刘红斌,万大平,胡德金.分形表面接触变形对部分膜润滑的影响[J].摩擦学学报,2008,28(3):244-247. Liu Hongbin,Wang Daping,Hu Dejin.Influence of Contact Deformation of the Fractal Surface on the Partial Film Lubrication[J].Tribology,2008,28(3):244-247. [13]陈奇.基于分形理论的汽车变速箱齿轮接触强度研究 [D].合肥:合肥工业大学, 2010. [14]Bhushan B.The Real Area of Contact in Polymeric Magnetic Media—II:Experimental Data and Analysis[J]. ASLE Transactions,1985,28(2):181-197. [15]陈辉,胡元中,王慧,等.粗糙表面分形特征的模拟及其表征[J].机械工程学报,2006,42(9): 219-223. Cheng Hui,Hu Yuan,Wang Hui,et al.Simulation and Characterization of Fractal Rough Surface[J].Chinese Journal of Mechanical Engineering,2006,42(9):219-223. [16]Mandelbrot B B.Stochastic Models for the Earth’s Relief, the Shape and the Fractal Dimension of the Coastlines,and the Number-area Rule for Islands[J]. Proceedings of the National Academy of Sciences,1975,72(10):3825-3828. [17]葛世荣,Tonder K.粗糙表面的分形特征与分形表达研究[J].摩擦学学报,1997,17(1):73-80. Ge Shirong,Tonder K.The Fractal Behavior and Fractal Rough Surface Characteristics and Fractal Expression Study[J]. Tribology, 1997,17(1):73-80. [18]陈奇,黄康,张彦,等.基于分形接触模型的齿轮接触强度影响参数分析[J].中国机械工程,2013,24(16):2208-2211. Cheng Qi,Huang Kang,Zhang Yan,et al.Analysis of Influence Parameters on the Gear Contact Strength Based Fractal Contact Model[J].China Mechanical Engineering,2013,24(16):2208-2211. [19]潘玉良,吴立群,张云电,等.分型模型参数和粗糙度参数Ra的关系[J].中国工程科学,2003,17(1):73-80. Pan Yuliang,Wu Liqun,Zhang Yundian,et al.Study of the Relationship between Fractal Model Parameters and Roughness ParametersRa[J].Chinese Engineering Science,2003,17(1):73-80. [20]李成贵, 袁长良.分形维数与表面粗糙度参数的关系[J]. 工具技术, 1997, 31(12):36-38. Li Chenggui,Yuan Changliang.The Relationship between Fractal DimensionDand Surface Roughness Parameters[J].Tool Engineering,1997,31(12):36-38. [21]Greenwood J A,Williamson J B P.Contact of Nominally Flat Surfaces[J].Proceedings of the Royal Society of London. Series A.Mathematical and Physical Sciences,1966,295:300-319. (编辑陈勇) Contact Model of Considering Two Rough Surface Fractal Characteristics Chen LifengLi QiCai ZhihuaGu Jinliang Hunan University of Science and Technology,Xiangtan,Hunan,411201 Based on the M-B fractal contact model,a contact model was built accounted for the fractal characteristics of two rough surfaces by constructing the contact coefficient.The analysis results show that the correction model has a good agreement with experimental date,and it is applicable to larger load.The correction model combines the characteristics of two rough surfaces,which fits better in with actual contact conditions,and it can provide reference to friction prediction, wear prediction,wear particle analysis and different roughness surface analyses. asperities;two rough surface;fractal characteristics;contact 2014-09-26 湖南省科技厅资助项目(2012TP4023-7);湖南科技大学博士启动基金资助项目(E50332) TH114DOI:10.3969/j.issn.1004-132X.2015.20.008 陈立锋,男,1977年生。湖南科技大学机电工程学院副教授。主要研究方向为机械传动及系统动力学。李奇,男,1991年生。湖南科技大学机电工程学院硕士研究生。蔡志华,男,1981年生。湖南科技大学机电工程学院讲师。谷金良,男,1983年生。湖南科技大学机电工程学院讲师。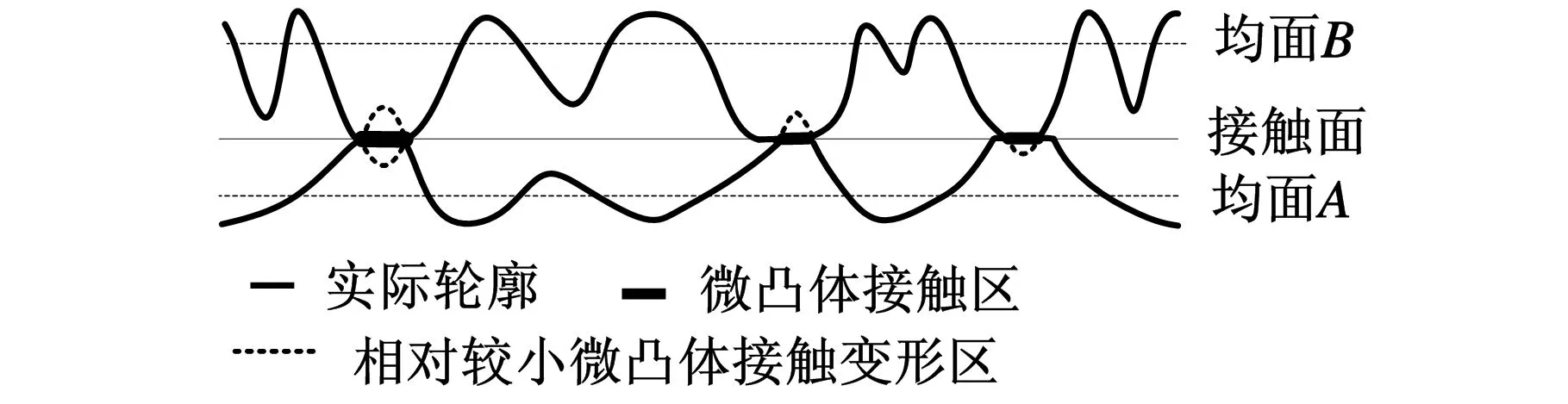
2 仿真分析
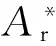
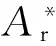
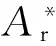
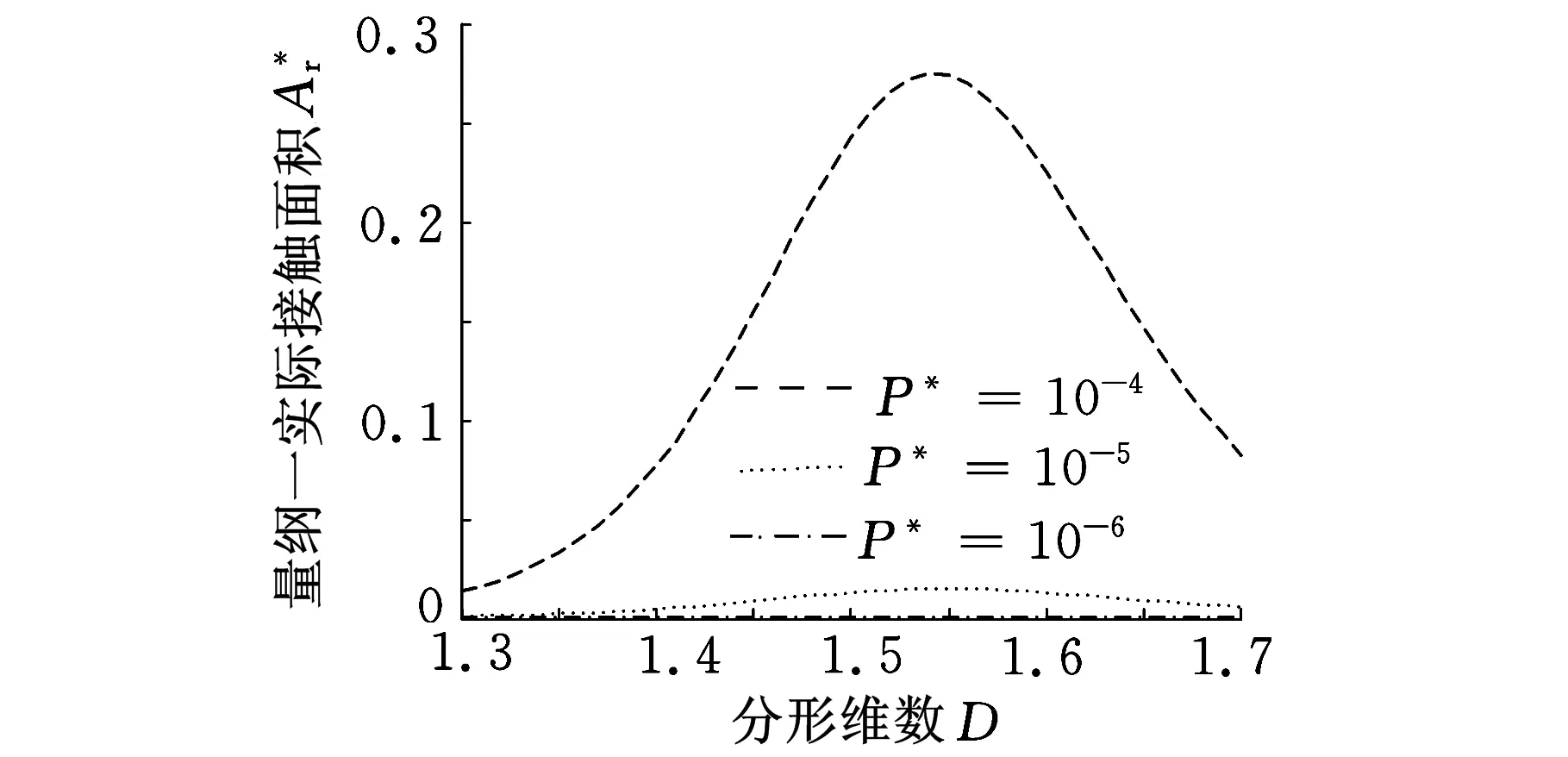
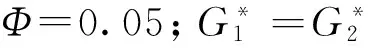

3 结论
