基于SMO-SVM的单点金刚笔钝化监测
2015-10-29李郝林迟玉伦
岳 泰 李郝林 迟玉伦
上海理工大学,上海,200093
基于SMO-SVM的单点金刚笔钝化监测
岳泰李郝林迟玉伦
上海理工大学,上海,200093
针对单点金刚笔在砂轮修整过程中易于钝化且难以检测的问题,使用支持向量机建立智能模型。为了得到建立模型所需的样本库,使用小波包分析等方法在线提取修整时声发射信号中的特征信息,并引入钝化平台直径定义钝化临界值。模型本身选用基于串行优化算法的支持向量分类机,使用交叉验证法搭配遗传算法以达到优化模型参数的目的。实验结果表明,该模型在分类精度和计算时间上均优于一般的智能模型,可以有效地监测金刚笔的钝化。
单点金刚笔;支持向量分类机;声发射信号;串行优化算法;钝化平台直径
0 引言
一直以来,磨削都是精密加工的主要实现方法。砂轮作为磨削加工的主角,其表面形貌直接决定着被加工工件的质量[1]。单点金刚笔是应用最为广泛的砂轮修整工具之一,它具有原理简单、易于操作和成本低廉的优点,但也常常因为自身的钝化而影响砂轮修整的质量。
判断金刚笔是否钝化的传统方法是离线的直接测量法,这种方法需要额外的人工操作以及停机拆装,过程繁琐且可靠性差[2];在线的光学监测法[3]可靠性好且原理简单,但却因为其光学系统的本身限制而不适合用于砂轮修整的恶劣环境中;利用声发射信号反映金刚笔的钝化信息,依靠类似于专家系统的模型实现对金刚笔钝化的智能判断,具有成本低、效率高的优点,受到国内外学者的广泛关注[2,4]。对比相关文献使用的监测方法发现,一般的统计过程法或实验回归法对训练样本本身分类较准确,对未知样本则误差较大[4-5];文献[6]中的隐马尔科夫模型法分类准确率较高,但模型较为复杂且鲁棒性差;文献[7]应用的贝叶斯网络模型易于构造和使用,但分类精度相对较低;文献[2]中人工神经网络在处理状态监测的非线性问题时效果较好,但由于其算法本身研究的是样本数趋于无穷大时的渐进理论,在处理样本数有限的实际问题时,存在分类精度差、易陷于局部最优等诸多问题。因此,分类方法的选择归结为寻找一种模型参数简单、分类准确率高、运算简洁且适合小样本的模式识别模型。
相比其他的智能模型,支持向量机[8](support vector machines,SVM)有着样本需求量少、模型参数简单、全局寻优求解等优势,但也存在着样本较多、训练时间长且模型参数难以选择等缺点。针对此问题,本文选择串行优化算法(sequential minimal optimization,SMO)来简化支持向量机训练中的二次规划问题,并将其应用于金刚笔的钝化监测。在模型输入样本的提取中,通过能够实时反映细微变化的声发射信号表征金刚笔状态,并使用滤波分段及小波包分析等方法提取特征信息。对于模型的输出部分,通过扫描电子显微镜观察金刚笔的形貌特征,并引入钝化平台等相关理论对金刚笔的钝化标准进行量化的评价。最后,将训练好的模型分别与标准支持向量机、最小二乘支持向量机以及神经网络进行对比。
1 单点金刚笔钝化监测模型的总体结构和流程
1.1硬件系统
硬件系统由砂轮修整、声发射信号采集以及金刚笔测量三部分组成。砂轮修整基于STUDER K-C33精密外圆磨床,使用L1102型金刚笔修整粒度为60目的平形铬刚玉砂轮(400 mm×50 mm×203 mm);在AE信号采集方面,选择AE传感器以及高速数据采集卡,配以计算机和辅助器件;金刚笔的测量则通过3D轮廓仪以及扫描电子显微镜实现。

图1 砂轮修整实验台
图1所示为金刚笔修整砂轮的实验现场,在整个过程中,选用相同的修整工艺以保证结果的准确性(表1)。考虑到金刚笔的修整深度对后文中的钝化判别和特征选择有较大影响,选取多个修整深度以增加实验的泛化性能。AE传感器依靠磁力固定在工作台上,距离修整区域100 mm。采集卡的采样频率设置为1 MHz,从而避免高频电气噪声,并尽可能多地采集有用的信号频段。此外,传感器和金刚笔的安装位置都被严格固定,以保证信号的稳定和实验的可靠性。

表1 修整工艺参数
1.2软件系统
如图2所示,软件系统有模型建立和模型使用两个步骤,模型的使用需要建立在模型建立的基础上,且每个步骤中各个模块的作用方式都不尽相同。整个软件系统包括输入模块、输出模块以及支持向量机模块。
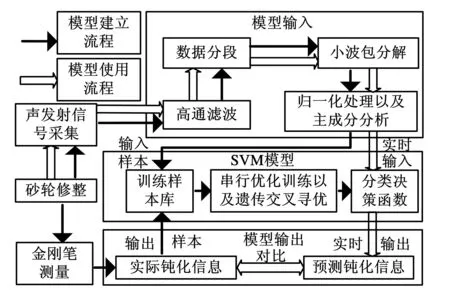
图2 金刚笔钝化监测系统结构和流程
2 模型输入:声发射信号的处理和提取
2.1信号预处理

(a)噪声信号
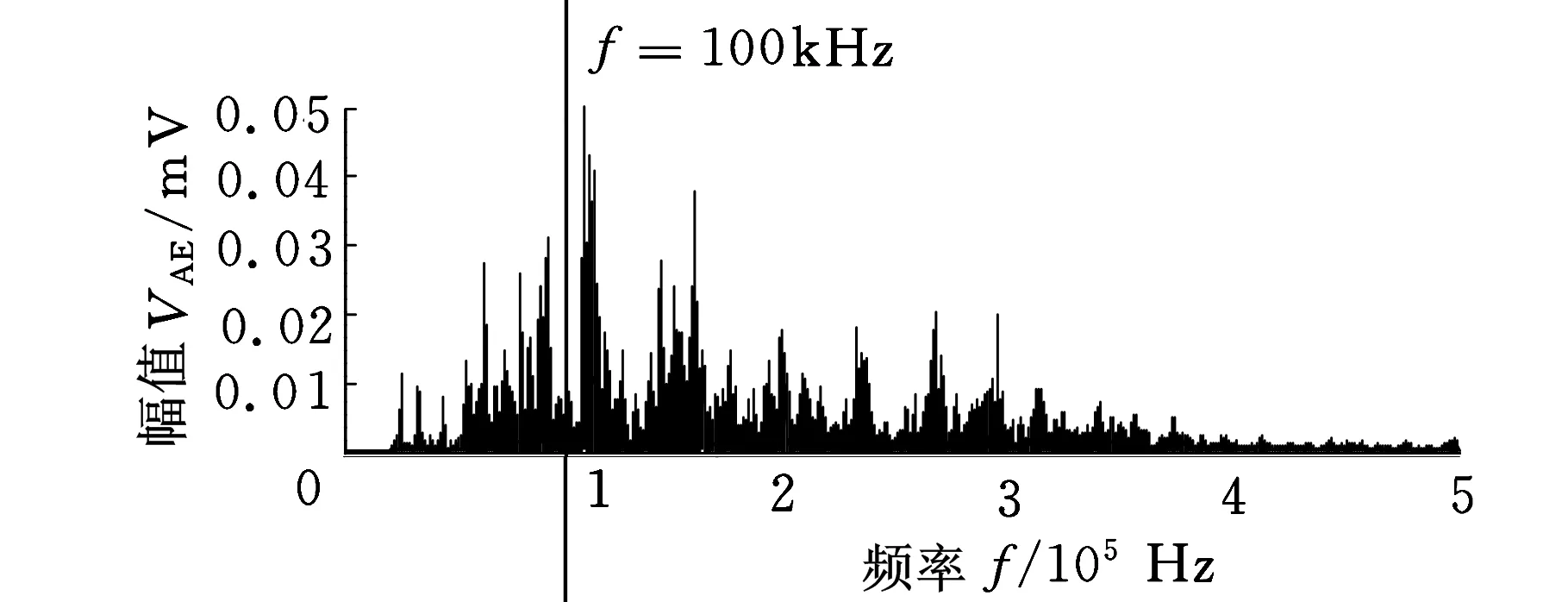
(b)修整信号图3 环境噪声和修整信号的频谱对比
在实验中,为了充分采集金刚笔状态信息,设置较高的采样频率,并且不可避免地采集了修整周期中的非修整部分。因此,对AE信号进行适当的预处理十分必要。通过观察发现,在修整周期的驶入过程中,AE信号只受环境噪声影响。因此,基于此时的AE信号对环境噪声以及修整信号进行频谱分析(图3)。可见,环境噪声集中在100 kHz以下,而修整信号则大多分布在100 kHz以上。根据此结论,设计了IIR高通数字滤波器,设置截止频率为100 kHz。由于AE信号有很强的突发性和衰减性,故需要滤波器有较强的衰减能力。因此,本文使用高阶的巴特沃斯型IIR滤波器来实现滤波[9]。
观察图4发现,经过滤波后的AE信号数据过于庞大,而且驶入、驶出、修整开始和修整结束这四个阶段的AE信号具有很强的不确定性,明显不能用于之后的特征提取。出于避免无用信号及减少计算量的目的,编写数控系统的内部PLC程序,使系统在周期开始时给出一个高电平信号,在周期结束时再恢复至低电平,通过此方波信号的上升沿和下降沿得到修整周期的时间信息。在修整周期确定的基础上,提取出修整周期中第10~15 s的稳定修整的信号并将其按秒分段,从而得到了数据量小且代表性强的AE信号。
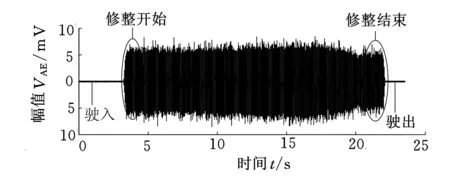
(a)时域图

(b)频域图图4 修整周期滤波后的时域和频域
2.2信号特征提取
AE信号的特征提取方法通常有时域法和频域法两种。本文综合以上两种方法,先对AE信号进行频域分段,再将特征明显频段的信号进行时域处理。相比单独的频域法或时域法,该方法可以更深层次地挖掘AE信号中的特征信息。
通常,小波分析和小波包分析都可以完成信号频域和时域的双尺度分解。一般的小波分解只是将低频的近似信号进行多次细化处理,未能提高高频细节信号的频率分辨率[10]。小波包算法将一对镜像滤波器组同时作用在近似信号和细节信号上,使它们同时进行分解,是小波算法的进一步深化。就金刚笔的状态监测来说,AE信号的低频部分大多是环境噪声,而高频才包含了真正有用的信息。因此,只对低频信号进行分解处理的小波分析显然不适用。
基于以上讨论,选用可以高频细分的小波包分析对信号进行处理。假设对信号进行n层的小波包分解,将原始信号按频率平均分解至2n个频段上,则可以得到同样数量的小波包系数(图5)。设Si,j表示第i层分解中第j个小波包系数,fs表示原始信号的采样频率,则Si,j包含着原始信号中fs(j-1)/2i+1到fsj/2i+1的时域信息。一般情况下,小波包系数相当于一个独立的时域信号。

图5 小波包分解原理
由小波包的定义可知,不同的小波包系数对应完全相同的频带宽度。这使得小波包系数的能量分布可以较好地反映原始信号的频谱特性。同时,在金刚笔的状态监测中,AE信号的频谱特性同金刚笔的钝化状态具有很强的联系。因此,利用小波包系数能量、频谱特性、金刚笔钝化状态三者之间的递推关系,将小波包系数的能量分布用于特征提取中。设第n层分解的总能量为E,第j个小波包系数Sn,j的能量为Ej,则有
(1)
(2)
其中,z表示小波包系数的离散点幅值,m表示采样点数,P为能量比,利用参数j和P可以得到各个小波包系数的能量关系。
基于以上流程,对经过预处理的AE信号进行小波包分析。多次实验结果表明,使用4层的小波包分析可以较好地识别频率特征,又能避免频段的过分细分。而在小波包基的选取上,针对AE信号的瞬态突发性以及在时域波形上的冲击特性,选择具有正交性、时域紧支性、频域快速衰减性,且时域波形和AE信号类似的多贝西一类小波(db1)。在参数确定的基础上,分别计算信号在金刚笔钝化和锐利两种状态下的能量分布,再通过对比绝对值的方法获取钝化和锐利之间的能量变化。
通过分析不同修整深度下的AE信号发现,随修整深度的减小,各个频段的能量变化值相应变小,但3、6、7、14所代表的频段一直保持变化最大的趋势(图6)。由此可知,上述四个频段即为所需的特征频段。根据小波包系数可以对应到时域的特点,分别计算它们的峭度作为特征样本。为了方便支持向量机的使用,对特征样本进行必要的归一化处理和主成分分析处理,设定归一化范围为-1~1,主成分分析阈值为95%。经过处理后,样本的维数从4降为3。
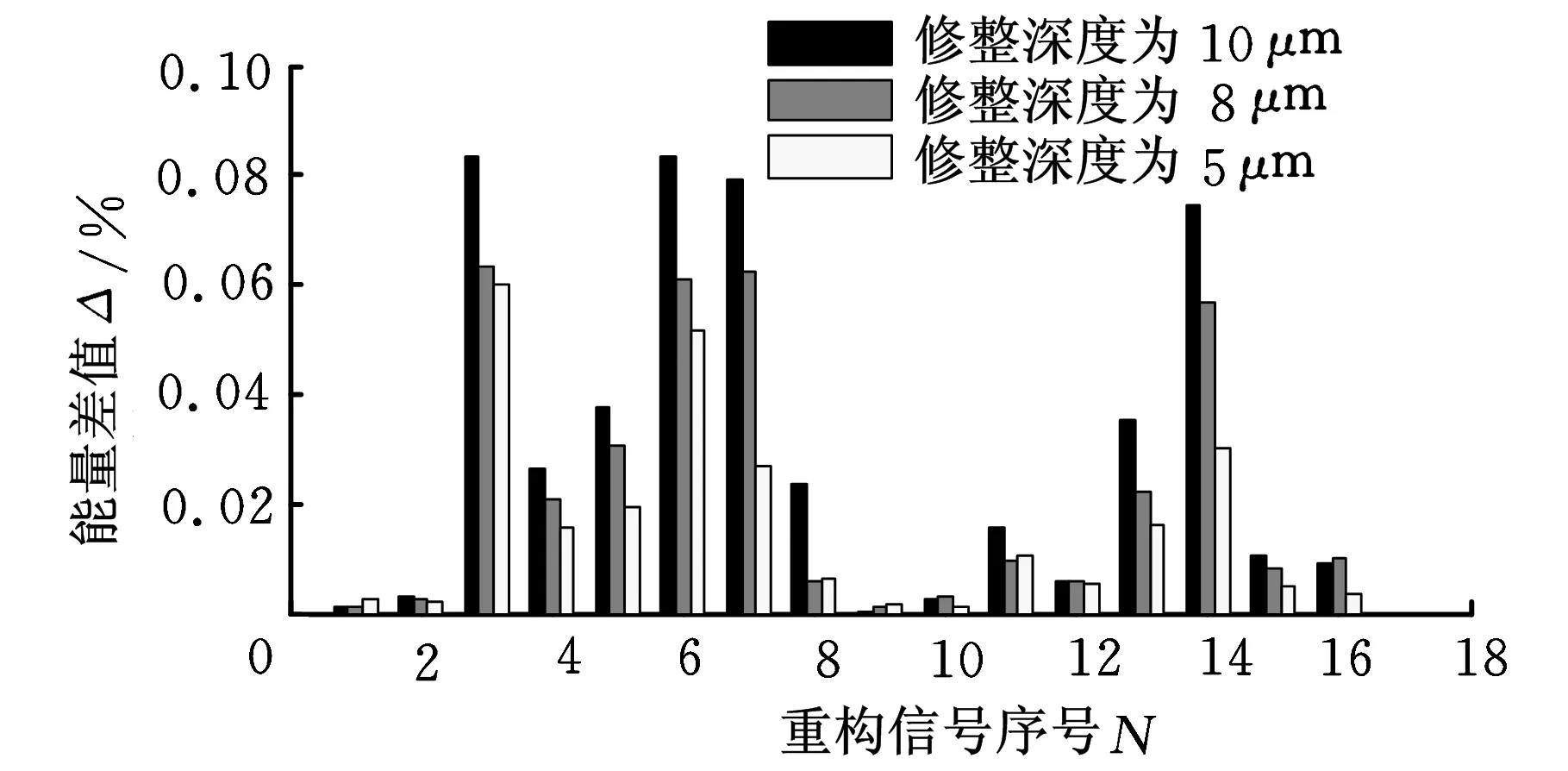
图6 金刚笔在不同修整深度下的能量差异对比图
3 模型输出:金刚笔钝化标准的确立和测量
3.1钝化标准的确立
在评价金刚笔是否钝化前,需要确定合理的钝化评判标准。本文根据分析金刚笔钝化对修整的影响来确定金刚笔的钝化标准,以此评价金刚笔的状态。
单点砂轮修整的直接评价指标主要有磨粒出刃高度和磨粒分布间隔两种。图7为锐利金刚笔和钝化金刚笔修整砂轮时的对比示意图。其中,hg是当前被修整砂轮的磨粒出刃高度,代表磨粒的纵向尺寸,其值越大,磨粒所能承受的磨削时间越长。fd为磨粒分布间隔,即砂轮转过一周时金刚笔的进给量,其值越大代表磨粒间隔越小,所对应的被磨削工件的表面粗糙度越低。磨粒分布间隔在数值上等于金刚笔进给速度vd和砂轮转速nw的比值。
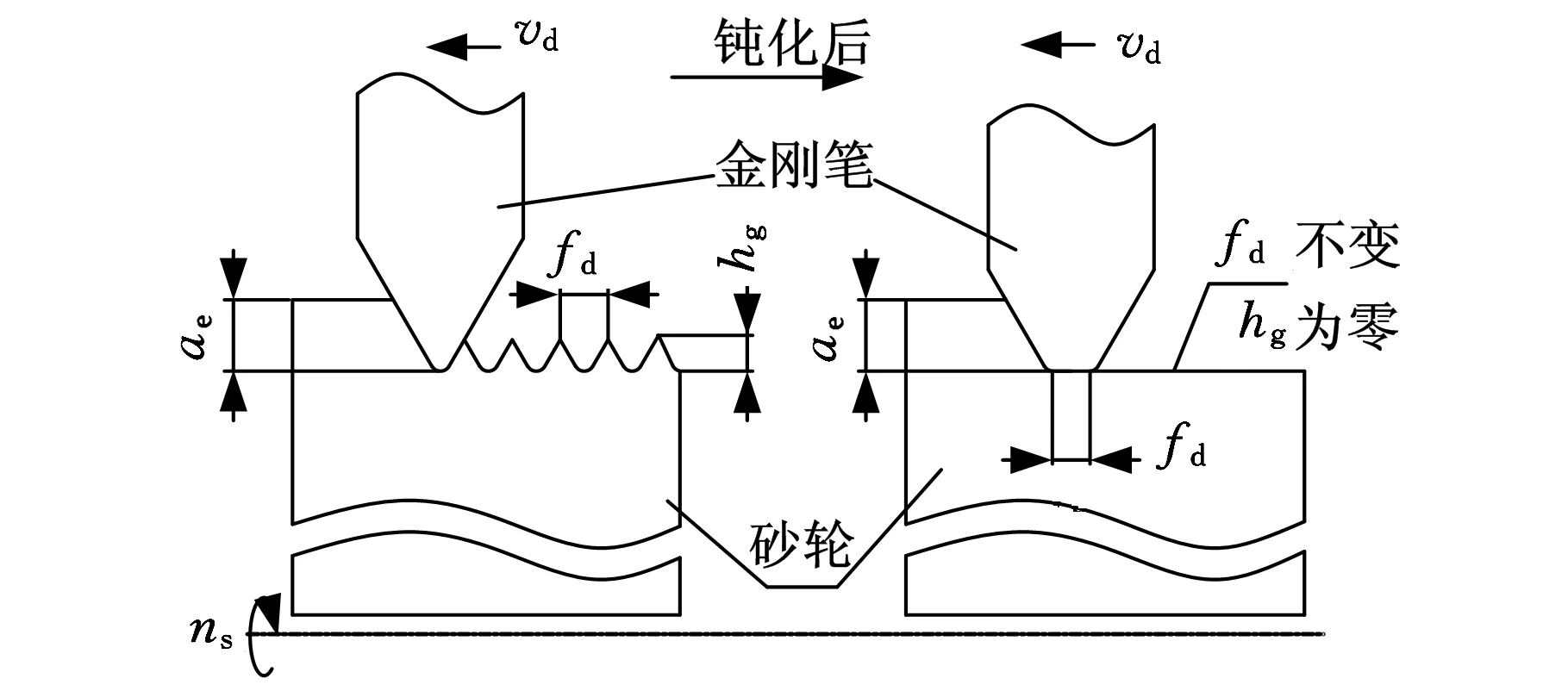
图7 不同状态下的金刚笔修整过程对比示意图
文献[11]提出,在不考虑金刚笔钝化的情况下,可将其刃端截面等效为二次抛物线轮廓。本文在此基础上考虑了钝化的影响,通过使用扫描电子显微镜对金刚笔进行轮廓评估(图8),发现金刚笔的钝化程度主要体现为刃端的圆形钝化平台大小。用dw表示钝化平台的等效直径,结合图7不难看出,在工艺参数不变的情况下,若dw的值和磨粒分布间隔fd相当,由于钝化平台的作用,砂轮在理论上将不会有任何磨粒产生,此时,金刚笔即达到钝化临界状态。使用表1中的修整工艺参数求得fd=0.0698 mm,所以当dw大于此值时,表示金刚笔已钝化。


图8 扫描电镜下的钝化金刚笔刃端
3.2实际钝化信息的测量
在砂轮修整实验中,即使是对金刚笔位置或角度的细微调整,都会对其钝化状态产生极大的影响。为了保证实验的可靠性和连续性,选择使用复印法配合3D轮廓仪来对金刚笔的钝化状态进行在位地测量。设置测量间隔为10个修整周期,在测量时,停止砂轮和金刚笔的运动,在不拆下金刚笔的情况下对其进行复印并评估。当测量到金刚笔钝化平台的等效直径约为0.0698 mm时,继续修整十个周期,再通过扫描电镜观察其细微状态,以确认其钝化。值得注意的是,由于每次测量后都需要重新对刀,而对刀后的前几个周期可能会出现修整深度过浅或过深的问题,所以需要确定信号稳定后,再进行AE信号的采集。
结合前文中AE信号的特征向量,设达到钝化标准的金刚笔所对应的样本为-1类,未钝化的为1类。至此,模型的样本库已建立。
4 支持向量机模型的建立和验证
4.1支持向量机的选择
本文的金刚笔状态监测是一个典型的非线性二值分类问题,考虑到模型的实用性要求,选择使用C型支持向量分类机进行分类。
假设给定两类训练输入样本xi和输出样本yi,代入C型支持向量分类机中可得到模型函数:
(3)
使用函数φ将输入向量映射至高维的特征空间以满足非线性分类的需要。其中,w为向量机决策超平面的法向量(对应为神经网络的权值),b为超平面的截距(对应为神经网络的截距),C表示对于错误分类的惩罚系数,ξi代表用于提高模型容错率的松弛变量。在模型函数的基础上,引入核函数的定义:
K(xi,xj)≡kT(xi)φ(xj)
(4)
顾名思义,核函数是支持向量机的核心,它赋予模型从低维向高维映射的能力以解决非线性问题。由于在高维空间中,样本之间只进行内积运算,所以只要满足Mercer条件,核函数就可以在原空间中映射高维空间的任何内积。在此过程中,可调参数并没有增加,从而避免因升维导致的维数灾难。常用的核函数有线性核函数、径向基(radial basis function,RBF)核函数、多项式核函数、多层感知核函数(sigmoid)四种。根据文献[12]的论述,线性核函数是RBF核函数的特殊情况;多项式核函数在样本维数较高时,会导致数值的畸形(趋于零或无穷);而Sigmoid核函数虽然性能和RBF核函数相当,但只有在其核矩阵对称半正定时才能发挥作用。因此,本文选择使用结构简单、性能优越的RBF函数作为模型的核函数。
在此基础上,引入拉格朗日函数对模型进行处理,得到了模型的对偶问题:
(5)
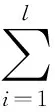
4.2串行优化算法的使用
串行优化算法是分解算法的特殊形式,即仅选择两个数据点作为工作集,考察其中不满足KKT条件的点,并启发式地将数据换入换出,反复迭代直到所有的数据都满足KKT条件[13]。此算法的优势在于可以通过两个数据点得到解析解,从而大大节省计算时间和储存空间。在训练SVM模型时,SMO算法每一次只选取两个拉格朗日乘子进行优化,再更新模型。首先确定根据式(5)得到当前的分类判别函数:
(6)
其中,b可以通过KKT条件中的互补松弛性求出。设第i个点的误差为Ei,则有
Ei=f(xi)-yi
(7)
在此基础上,可以求解两个乘子的二次规划。分别设α1和α2对应两个乘子 ,基于以上超线性约束和超区域约束,可以得到两个乘子在类别相同时和不同时的关系,进一步确定相关目标函数并将偏导数置零,可得到两个乘子的解:
(8)
η=K(x1,x1)+K(x2,x2)-2K(x1,x2)
此外,需要简化KKT条件并得到SMO算法的停机准则:
(9)
当pi为零时,即表示所有样本满足KKT条件,算法停止。拉格朗日乘子的选择基于启发式算法,分别针对两个乘子设计两个嵌套的循环以保证模型的决策函数在优化过程中有明显的更新。初始化α=b=0,α1所对应的外部循环只考虑违反KKT条件的样本,首先在非边界样本中选择,若没有找到,则在所有样本中串行选择;若仍没有找到,则退出程序。在找到α1后,进入算法的内部循环,从违反KKT条件的非边界样本中找出使|E1-E2|最大的α2,重复进行两个循环直到满足停机准则。
4.3结果验证和对比
前文已确定了模型的类型结构以及所需的样本库,现只需训练模型参数即可完成SVM模型的构建。为了提高模型泛化能力,不失一般性地从样本库中随机选取100组样本作为训练集,100组样本作为测试集。在训练时,针对惩罚系数和径向基宽度系数难以选择的问题,应用具有较好收敛性的遗传算法对模型参数进行全局优化,同时配合交叉验证法以充分利用训练集。设置种群数量为20,进化代数为100,指定分类精度为适应度函数,将训练集分为5组进行交叉验证。
图9和图10分别为训练样本在三维空间中的分布图以及测试样本经过SVM分类后的混淆矩阵。不难看出,训练样本在分布上具有明显的非线性,单单从三维空间中观察很难找到规律。
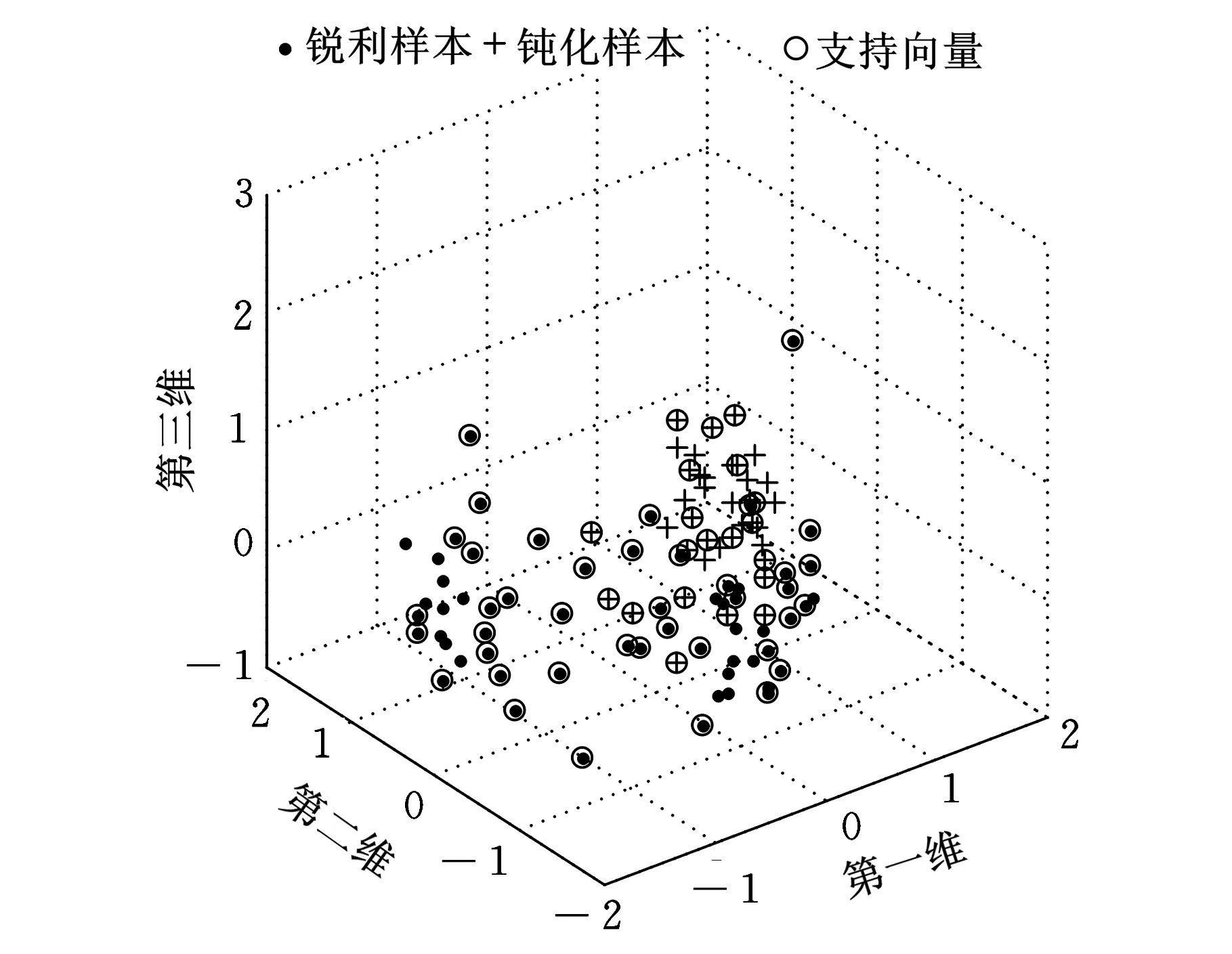
图9 支持向量机训练样本分布
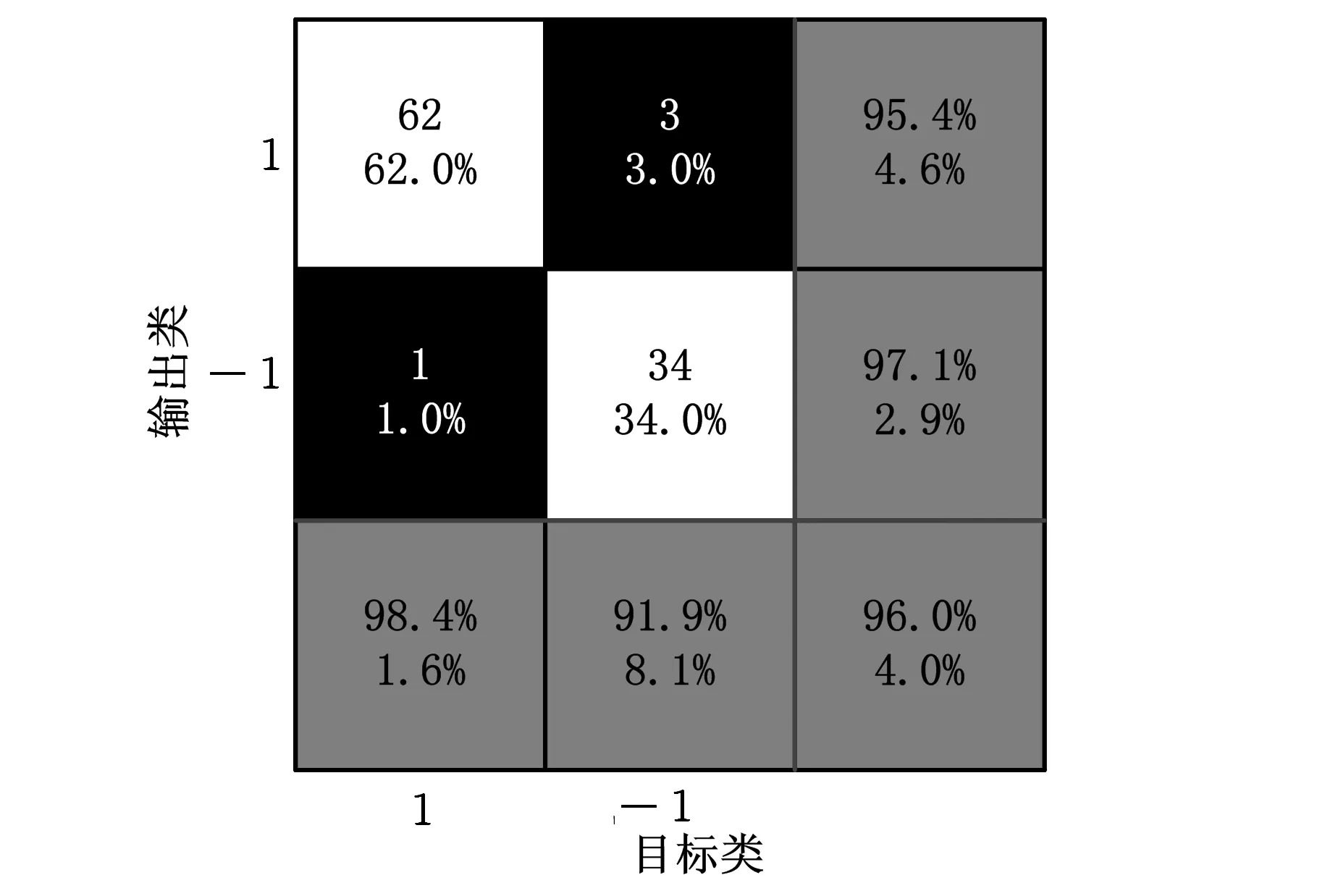
图10 分类结果的混淆矩阵
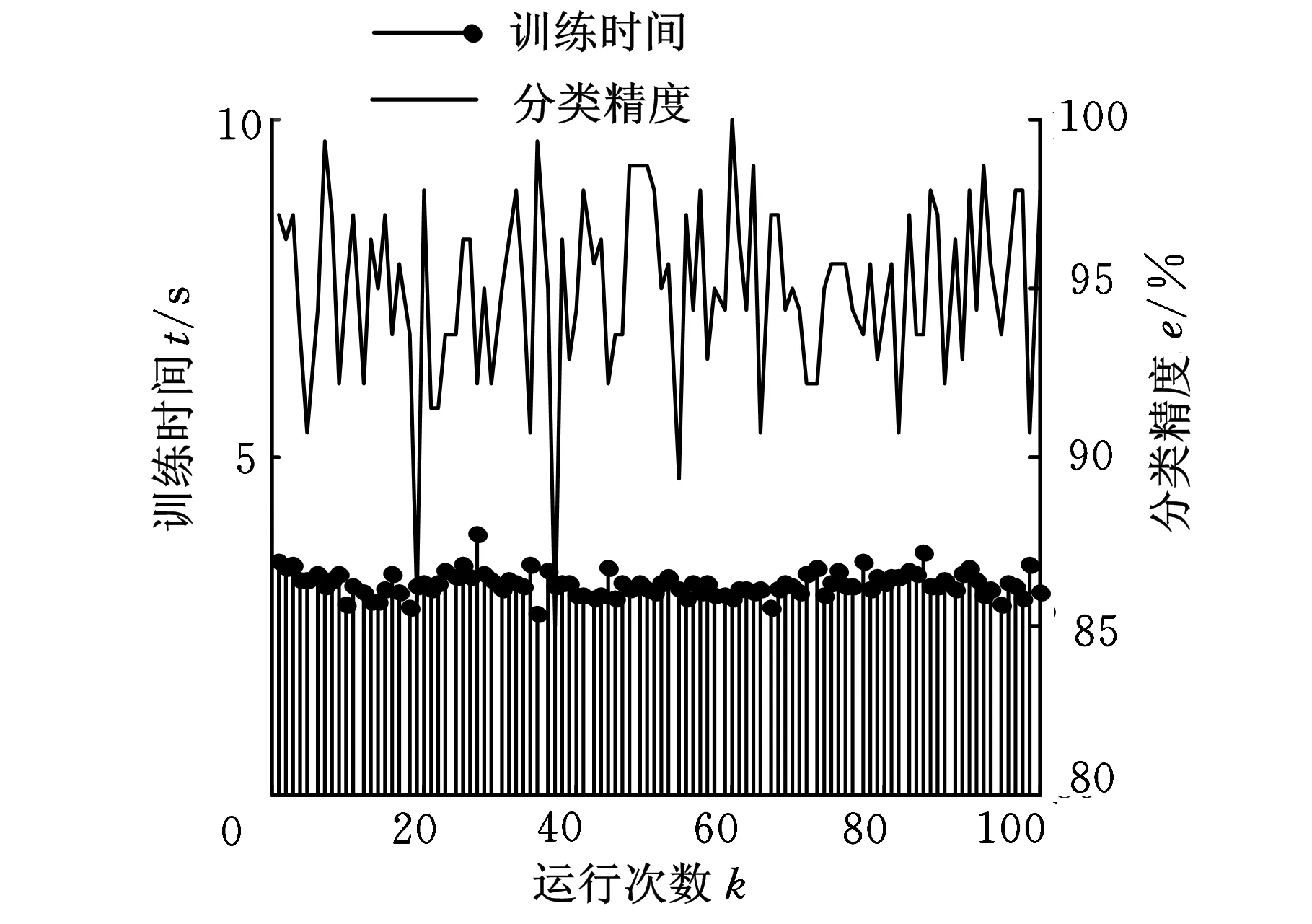
图11 SMO-SVM模型性能
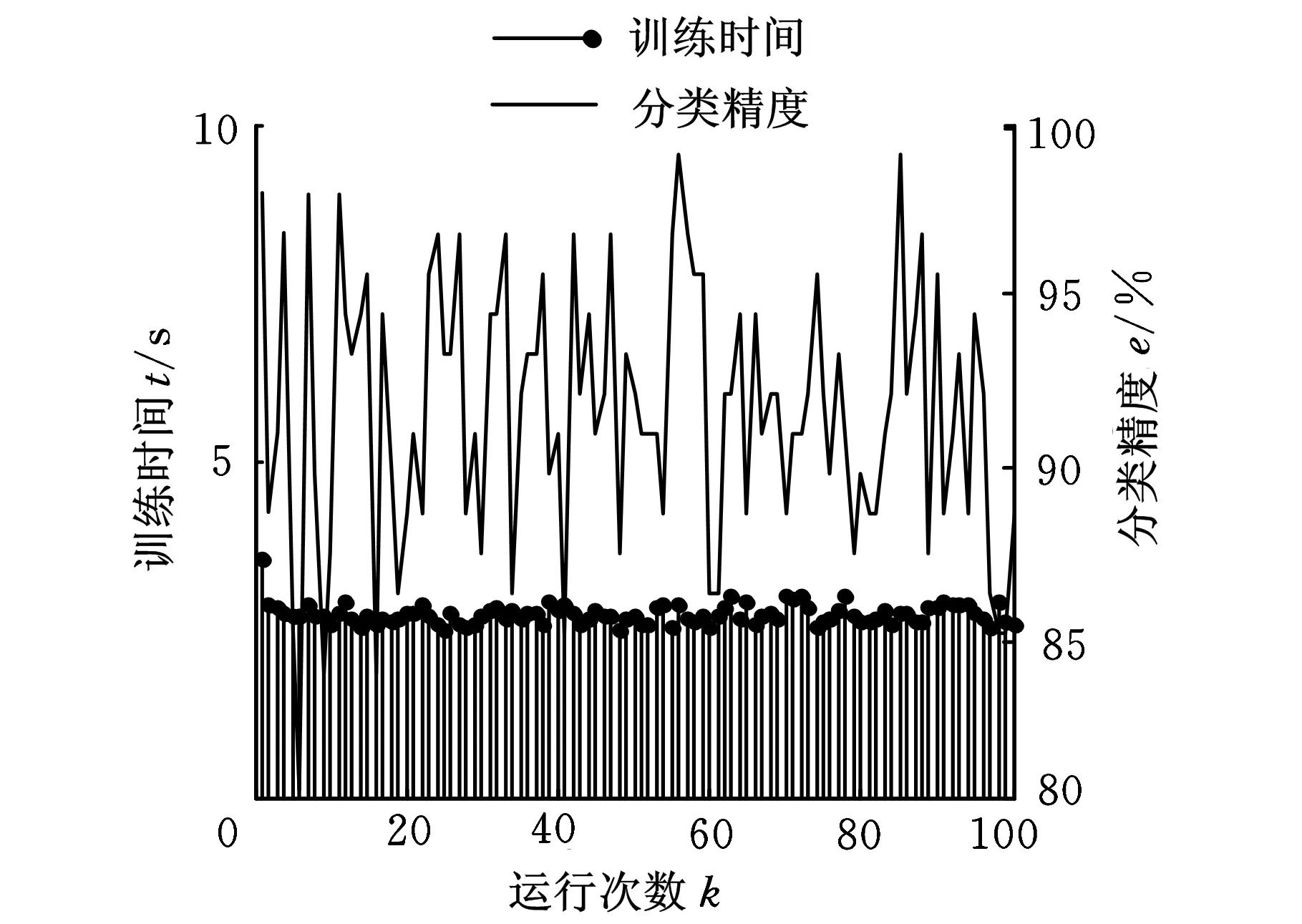
图12 LS-SVM模型性能
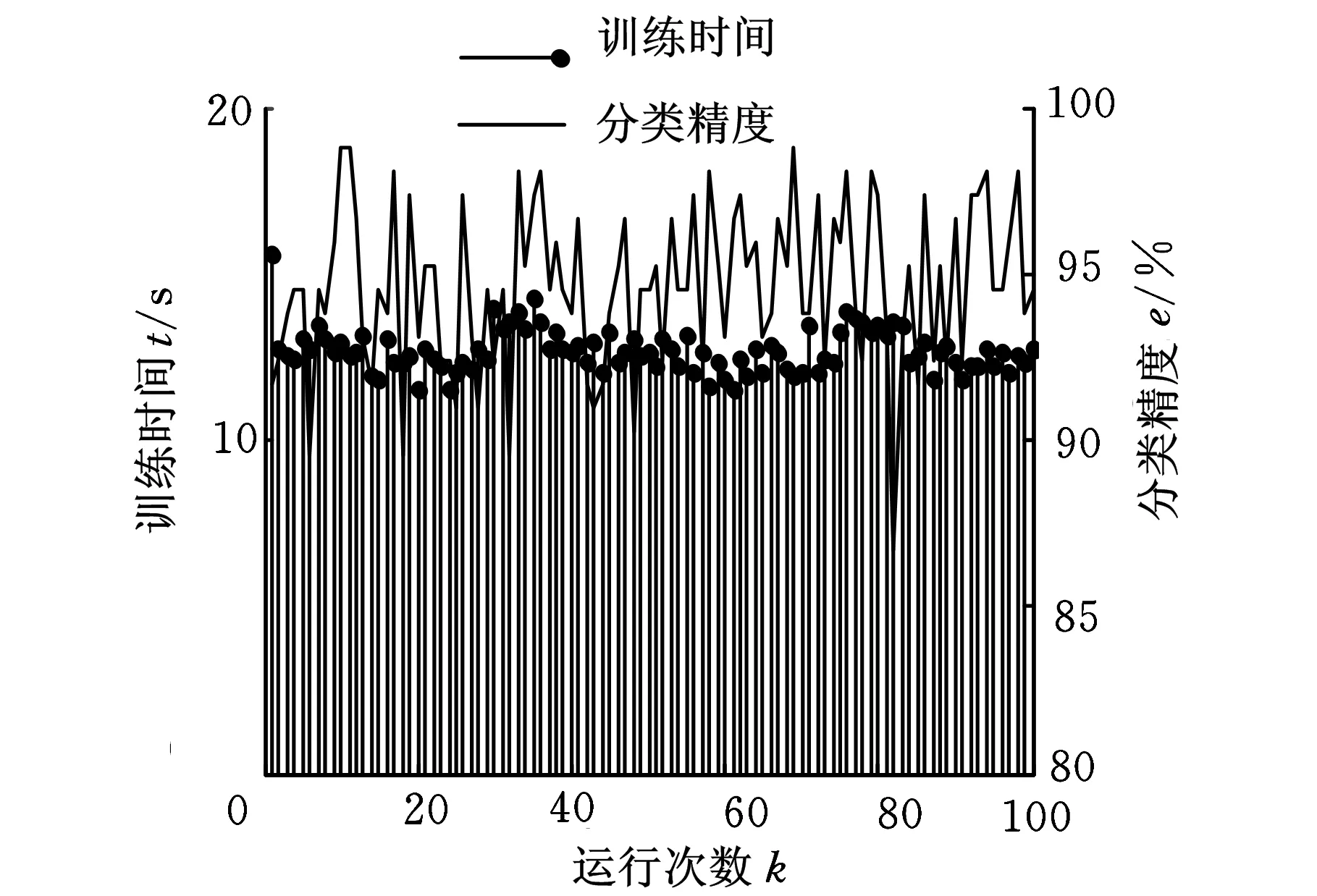
图13 O-SVM模型性能
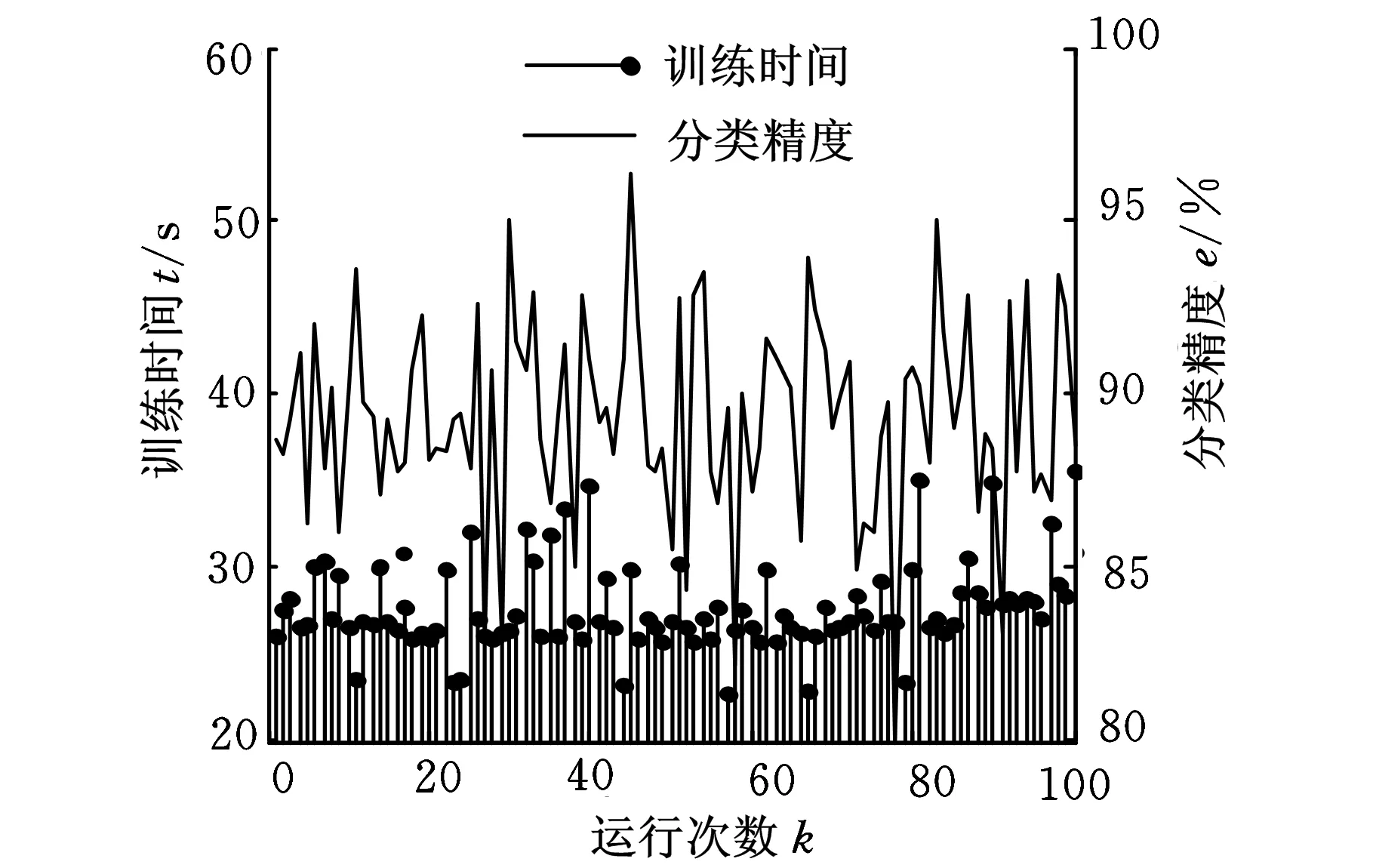
图14 BPANN模型性能
为了验证模型的分类性能,使用修整深度为5 μm的样本对串行优化支持向量机(SMO-SVM)、最小二乘支持向量机(LS-SVM)、原始支持向量机(O-SVM)以及BP神经网络(BPANN)进行训练和验证,并都使用遗传算法进行交叉寻优,得到了图11~图14所示的性能比较结果。可见,在训练时间上,SMO-SVM模型和LS-SVM模型相当,BPANN模型和O-SVM模型有较大劣势,且BPANN模型相对于其他模型有较强的不稳定性。而在分类精度上,SMO-SVM模型和O-SVM模型相当,明显优于LS-SVM模型和BPANN模型。综合评价后得到,本文所使用的SMO-SVM模型在整体性能上具有明显的优越性。
分析对比结果发现,模型性能的差异主要是因为算法本身的不同。BPANN模型在训练过程中参变量过多,每个神经元的各个参数都需要依据梯度最大方向更新,从而使得训练时间变长。神经网络的分类精度较低的问题,则归结于其经验误差最小化原理和基于无限大样本的特点。由于修整过程中的样本数目较少,使得神经网络可不能有效地对未知样本进行判断。LS-SVM模型、SMO-SVM模型以及O-SVM模型的差别在于它们针对训练中的二次规划问题使用了不同的方法。LS-SVM模型将二次规划问题简化为一个线性方程,失去了凸优化的最优解特性,牺牲了分类精度却大大加快了训练速度。O-SVM模型的分类性能较好,但是由于二次规划的计算量较大而导致训练时间较长。SMO-SVM模型利用串行优化算法巧妙地简化了二次规划问题,并采用启发式的算子搜索,所以能在较短的时间内训练出分类精度较高的模型。通过计算可知,对于本文的SMO-SVM模型,分类精度和金刚笔的修整深度成正比。在特征最不明显的5 μm修整深度的样本中,模型的平均训练时间仅为3.3893 s,平均分类精度可达到95.2571%,这充分证明该模型可以有效地监测金刚笔的钝化状态。
5 结论
(1)钝化平台直径可以较好地量化评价金刚笔的钝化程度。
(2)小波包分解可以有效地从高频声发射信号中提取特征信息。
(3)基于串行优化算法的支持向量机在金刚笔钝化分类上具有比原始支持向量机、最小二乘支持向量机以及神经网络更优越的性能。
[1]Marinescu M,Hitchiner E,Uhlmann,et al.Handbook of Machining with Grinding Wheels[M].Boca Raton:CRC/Taylor & Francis Group,2007.
[2]Martins C H R,Aguiar P R,Frech A,et al.Tool Condition Monitoring of Single-point Dresser Using Acoustic Emission and Neural Networks Models[J].Instrumentation and Measurement,2014,63(3):667-679.
[3]Habrat W,Batsch A,Porzycki J.Monitoring of the Single Point Diamond Dresser Wear[J].Archives Civil Mech.,2005,5(1):13-18.
[4]Shi D,Axinte D A,Gindy N N.Online Machining Process Monitoring Using Wavelet Transform and SPC[C]//Proceedings of the IMTC.Sorrento,2006:2081-2086.
[5]Karpuschewski B,Wehmeier M,Inasaki I.Grinding Monitoring System Based on Power and Acoustic Emission Sensors[J].Annals of the CIRP,2000,49(1):235-240.
[6]Liao T W,Hua G G,Qu J,et al.Grinding Wheel Condition Monitoring with Hidden Markov Model-based Clustering Methods[J].Machining Science and Technology,2006,10(4):511-538.
[7]林峰,焦慧锋,傅建中.基于贝叶斯网络的平面磨削状态智能监测技术研究[J].中国机械工程,2011,22(11):1269-1273.
Lin Feng,Jiao Huifeng,Fu Jianzhong.Research on Intelligent Monitoring Technique of Machining State for Surface Grinder Based on Bayesian Network[J].China Mechanical Engineering,2011,22(11):1269-1273.
[8]张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,26(1):32-42.
Zhang Xuegong.Introduction to Statistical Learning Theory and Support Vector Machines[J].Acta Automatica Sinica,2000,26(1):32-42.
[9]Yang Z S,Yu Z H.Grinding Wheel Wear Monitoring Based on Wavelet Analysis and Support Vector Machine[J].The International Journal of Advanced Manufacturing Technology,2012,62(1/4):107-121.
[10]崔锦泰.小波分析导论[M].西安:西安交通大学出版社,1997.
[11]Doman D A,Warkentin A,Bauer R.A Survey of Recent Grinding Wheel Topography Models[J].International Journal of Machine Tools and Manufacture,2006,46(3/4):343-352.
[12]Keerthi S S,Lin C J.Asymptotic Behaviors of Support Vector Machines with Gaussian Kernel[J].Neural Computation,2003,15(7):1667-1689.
[13]Keerthi S S,Shevade S K,Bhattacharyya C,et al. Improvements to Platt’s SMO Algorithm for SVM Classifier Design[J].Neural Computation,2001,13(3):637-649.
(编辑陈勇)
Tool Wear Monitoring of Diamond Single-point Dresser Based on SMO-SVM
Yue TaiLi HaolinChi Yulun
University of Shanghai for Science and Technology,Shanghai,200093
An intelligent monitoring model was proposed based on support vector machine to solve the problem of identifying the wear of diamond single-point dresser in the dressing process of grinding wheel.To obtain the required samples for modeling,wavelet packet analysis was used to extract the feature informations from acoustic emission signals during the dressing process,and the diameter of wear platform was employed to define the threshold of dresser wear. Besides, for improving the practicability of the model, a SOM method was applied to train the support vector classifier,the parameters of the model were selected by using genetic algorithm as well as cross validation method. Experimental results show that the model has higher performance than general intelligent model, and can monitor the wear of the dresser effectively.
diamond single-point dresser;support vector classifier;acoustic emission signal;sequential minimal optimization(SMO) method;diameter of wear platform
2015-04-20
国家科技重大专项(2013ZX04008-011)
TH117.1DOI:10.3969/j.issn.1004-132X.2015.20.007
岳泰,男,1992年生。上海理工大学机械学院硕士研究生。主要研究方向为精密检测技术。李郝林,男,1961年生。上海理工大学机械工程学院教授、博士研究生导师。迟玉伦,男,1983年生。上海理工大学机械工程学院讲师。
