随机变量和非独立区间变量下的可靠性序列迭代算法

潘柏松　谢少军　Du Xiaoping　梁利华

1.浙江工业大学,杭州,3100142.Missouri University of Science and Technology,Rolla,USA

随机变量和非独立区间变量下的可靠性序列迭代算法

潘柏松1谢少军1Du Xiaoping2梁利华1

1.浙江工业大学,杭州,3100142.Missouri University of Science and Technology,Rolla,USA

针对机械系统中输入变量存在随机变量和区间变量混合的情况，考虑区间变量的非独立性，提出高效混合可靠性分析方法。区间变量使可靠性分析问题变为双层优化问题。为降低双层优化和非独立区间变量对可靠性计算效率的影响，提出了高效序列迭代计算策略，基于椭球模型描述的非独立区间变量，提出将非独立区间变量转换为独立区间变量的方法，并利用二次泰勒近似方法，将区间分析问题转换为易求解的二次规划问题。算例结果表明，所提出的可靠性序列迭代算法具有较高的计算效率和精度；可靠性分析结果受区间变量独立性假设的影响，区间变量独立可导致较保守的可靠性分析结果。

可靠性分析;椭球模型;非独立区间变量;序列迭代算法

0　引言

为克服传统可靠性分析及设计在处理认知不确定性方面的不足，学者们发展了较多非概率建模理论,如可能性理论[3]、证据理论[4]、凸集模型[5],以及概率建模理论——贝叶斯理论[6]。作为凸集模型的特例，区间模型[7]在实数轴上规定了认知不确定性变量可变区间的上下限。在工程应用中,仅有的信息为不确定性变量处于某个区间内的情况十分常见,如结构几何尺寸、运动副间隙、测量误差、计算误差等，基于区间模型的可靠性研究已有诸多报道。如Du等[8]提出了随机变量和区间变量混合型可靠性设计方法;江涛等[9]基于区间模型提出了非概率可靠性指标的一维优化方法;姜潮等[10]针对分布参数存在区间变量的混合不确定问题，提出了一种时变可靠性分析方法。为提高区间模型计算效率,Du[11]基于一次二阶矩法提出了一种高效的混合型可靠性分析方法;Jiang等[12]提出了序列非线性区间规划方法。

但上述文献均假设区间变量是相互独立的,而在实际工程中,某些区间变量存在一定的相关性，是非独立的，如描述结构几何尺寸的区间变量和结构质量的区间变量一般存在相关性，较大的几何尺寸区间变量意味着较大的结构质量区间变量,反之亦然；两个区间变量可单独取区间的最大值或最小值，但两者不同时为最大值或最小值;与几何尺寸区间变量和结构质量区间变量的相关性相反,某区间变量取值较大表明另一个区间变量较小。在一般常识意义上,本文将这三种情况的相关性分别称为正相关性、零相关性和负相关性。考虑区间变量的非独立性具有非常重要的研究意义,但目前关于非独立区间变量的可靠性研究较少。Du[13]针对机构运动副,基于物理关系式推导获得非独立区间变量描述模型——等式与不等式约束条件,提出了一种随机变量和非独立区间变量的混合型可靠性设计方法。Jiang等[14]采用多维度平行六面体区间模型，考虑了区间变量为独立或非独立的情况,提出了一种新的非线性区间规划方法，但该规划方法未考虑系统中同时存在随机变量和区间变量的混合情况。

本文针对系统输入变量存在随机变量和非独立区间变量混合的情况，基于条件概率法和椭球模型，提出了混合型可靠性分析模型及高效可靠性分析算法。为解决非独立区间变量对计算效率的影响,利用线性变换,将非独立区间变量转换为独立区间变量；为解决概率分析和区间分析双层循环计算效率低下难题，提出了序列迭代算法。

1　椭球模型

椭球模型属于凸集模型,最早由Ben-Haim等[5,15]提出。椭球模型可方便地描述非独立区间变量,在许多实际应用中,椭球模型较其他模型具有更多的优点[16-17]。

设Y=(Y1,Y2,…,YNY)T为区间变量矢量,区间变量个数为NY。由于在复杂机械系统中,区间变量的维度一般较高,而且区间变量之间的非独立关系往往不同(如某些区间变量服从正相关关系,而某些区间变量是相互独立的),因此,需根据不同的独立性特点,将区间变量归入不同的组。设经分组后,区间变量矢量可表示为Y=(Y1,Y2,…,YNg)T,其中Ng为组的数量,Yi为第i组区间变量矢量。基于分组后的区间变量,椭球模型可描述为

(1)

因可行域S由Ng个椭球组成,故该模型也称为多椭球模型,单个椭球模型的变量不超过3个。多椭球模型可方便地描述具有不同独立特性的区间变量。如当某区间变量是独立的，则椭球模型可退化为区间模型；当两个区间变量存在相关性，则椭球模型可退化为椭圆模型。图1给出了3个区间变量构成的不同几何形状的可行域S：在图1a中，3个变量是相互独立的；在图1b中,Y3是独立的变量,Y1和Y2存在相关性,是非独立的;在图1c中,3个变量存在相关性,是非独立的。

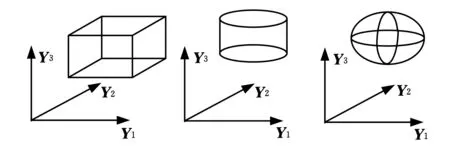
(a)三变量相关独立(b)一变量独立，两变量相关(c)三变量相关图1　椭球模型

因各个区间变量的单位不同,区间大小不同,不便于分析计算,故将区间变量转换为量纲一变量:

(2)

则分组后的区间变量矢量Y=(Y1,Y2,…,YNg)T转换为V=(V1,V2,…,VNg)T。

多椭球模型可相应地表示为

(3)

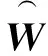
(4)

(5)

2　可靠性分析模型

设系统极限状态函数为

G=g(X,Y)

(6)

其中,X=(X1,X2,…,XNX)T为随机变量矢量,随机变量的个数为NX;Y=(Y1,Y2,…,YNY)T为区间变量矢量,区间变量的个数为NY。

将区间变量的变换关系式代入式(6),则极限状态函数可写为G=g(X,E)。设G<0时系统失效,则系统失效概率Pf可表示为Pf=Pr{g(X,E)<0}。因未知区间变量V的概率分布,故不能获得准确的失效概率Pf。利用条件概率公式,可得失效概率Pf的最小值Pf min和最大值Pf max的计算公式:

Pf min=Pr{gmax(X,E)<0|E∈S|

(7)

Pf max=Pr{gmin(X,E)<0|E∈S}

(8)

其中,gmax(X,E)和gmin(X,E)分别表示在可行域S内极限状态函数的全局最大值和最小值。

由式(7)和式(8)可见,当系统极限状态函数的不确定性输入变量存在随机变量和区间变量时，系统失效概率的最小值和最大值分别为最大极限状态函数和最小极限状态函数的失效概率。相对于传统可靠性分析问题，该可靠性分析问题涉及双层分析循环：内循环为区间分析，在可行域S内搜寻极限状态函数的极限值；外循环为概率分析，求解最大极限状态函数或最小极限状态函数的失效概率。双层分析循环增加了可靠性分析问题的复杂性，降低了可靠性分析的计算效率，尤其当极限状态函数由计算机数值仿真模型(如有限元模型、流体动力学模型等)隐式表述时。为提高随机变量和非独立区间变量混合情况下的可靠性分析计算效率，本文提出了基于一次二阶矩法的高效可靠性分析方法。

3　可靠性分析方法

一次二阶矩法是一种针对不确定性输入变量均为随机变量的近似可靠性分析方法,它包括两个关键步骤:将随机变量转换为独立的标准正态随机变量;搜寻最大概率点(MPP),在最大概率点对极限状态函数作线性近似,最后求得可靠性指标。

因一次二阶矩法的计算效率和准确度令人满意,故在实际工程中已获大量应用，在此选用一次二阶矩法进行可靠性分析。在一次二阶矩法中，最大概率点u*的数学优化模型为

(9)

其中,U=(U1,U2,…,UNX)T为独立的随机变量矢量,服从标准正态分布,由随机矢量X经Rosenblatt变换获得。

e*为经变换后的区间变量最优点,由内层区间分析求得:

(10)

或

(11)

一旦寻得最大概率点,则系统失效概率的最小值和最大值分别为

Pf min=Pr{(gmax(X,E)<0|E∈S}=

Φ(-((u*)Tu*)1/2)

(12)

Pf max=Pr{gmin(X,E)<0|E∈S}=

Φ(-((u*)Tu*)1/2)

(13)

其中,Φ(·)为标准正态分布函数。

图2给出了失效概率的计算流程,内层区间循环嵌于外层概率分析循环。由图2可见，概率分析和区间分析的算法效率共同决定了可靠性分析的整体计算效率，为此，本文提出了高效的序列迭代算法，该算法由随机变量迭代和区间变量迭代两部分组成。在随机变量迭代中，采用了高效的iHLRF迭代算法；在区间变量迭代中，将非独立区间变量转换为独立变量，对极限状态函数作二次近似，将区间分析问题转换为二次规划问题，最终利用梯度投影法，求得极限状态函数的极限值。

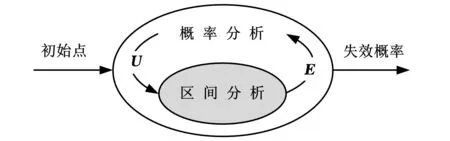
图2　双层循环计算流程

3.1iHLRF迭代算法[18]

作为HLRF算法的改进算法，iHLRF算法引入了评价函数，用于调整每一步的迭代步长，解决了HLRF在处理高非线性响应函数时收敛困难的问题。因iHLRF算法收敛快速，并具有较好的稳健性,故在工程中被广泛应用。

设当前迭代步骤为k+1，则最大概率点的迭代公式为

uk+1=uk+αkdk

(14)

其中,αk为迭代步长，dk为迭代方向，其计算式为

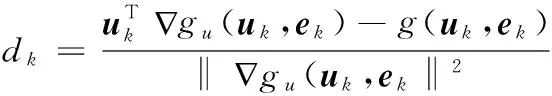
(15)

迭代步长αk通过求评价函数最小值获得，评价函数为

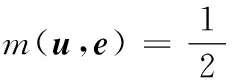
(16)

其中,c为常数,满足c>‖u‖/‖gu(u,e)‖。

在实际应用中，为减小计算量,在确定αk时无需准确搜寻评价函数最小值,而只需满足评价函数足够小条件，迭代步长αk由以下计算式确定：

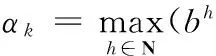
(17)

在此取b=0.5,c=2(‖u‖/‖gu(u,e)‖)。

3.2区间迭代算法

为提高效率,利用Karush-Kuhn-Tucker最优化条件(KKT条件)事先判断区间变量迭代初始点是否为优化点。若满足KKT条件，则跳过区间迭代;若不满足,则实施区间迭代。因在可靠性分析中工程师往往关心最坏的情况,即最大失效概率，故以下仅具体描述了求解Pf max的区间迭代算法。

基于式(5)给出多椭球模型的参数化表达式,将非独立区间变量E转换为相互独立的区间变量P,转换关系式表示为P=h(E),具体表达分以下三种情况：

(1)当i个椭球模型中有三个区间变量Ei1、Ei2和Ei3，则令Ei1=Pi1sinPi2cosPi3,Ei2=Pi1sinPi2sinPi3，Ei3=Pi1cosPi2,其中Pi1∈[0,1],Pi2∈[0,π]，Pi3∈[0,2π]；

(2)当i个椭球模型中有两个区间变量Ei1、Ei2,即椭球模型退化为椭圆模型,则令Ei1=Pi1cosPi2,Ei2=Pi1sinPi2,其中Pi1∈[0,1],Pi2∈[0,2π]；

(3)当椭球模型中只有单个区间变量,即椭球模型退化为区间模型,表明该区间变量是独立的,则Ei1=Pi1,其中Pi1∈[-1,1]。

将经上述变换后的区间变量代入极限状态函数g(U,E),g(U,E)可表述为g(U,P),则式(11)可重写为

(18)

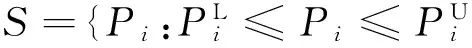
设l为区间迭代循环次数,在迭代初始时,令l=0,初始点pl=0=h(ek)。在区间迭代循环中,随机变量uk+1保持不变，故在以下给出的区间迭代算法中,省略随机变量。设当前区间分析循环次数为l,在当前迭代点pl,极限状态函数作二次泰勒近似,式(18)转换为二次规划问题：

(19)

其中,Hl为海森矩阵。因计算Hl需求极限状态函数的二阶偏导数,计算效率较低,故本文采用阻尼BFGS公式近似Hl。

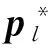
(20)

其中,κl为迭代步长,为保证全局收敛性,利用回代法求解κl,即重复κl←κlρ,直至新迭代点满足Armijo条件,即

(21)

在此取ρ=0.8,η=1×10-4。

若新迭代点pl+1满足KKT条件,则区间迭代停止,令ek+1=h-1(pl+1),其中h-1(·)表示区间变量变换关系式的逆变换;否则,令l←l+1,继续区间迭代。

本文提出的基于一次二阶矩法的可靠性序列迭代算法的步骤可整理如下：

(1)输入初始点u0和e0,初始化迭代次数k=0,初始点均取为零向量；

(2)计算uk+1=uk+αkdk;

(3)判断ek是否满足KKT条件，若满足,则令ek+1←ek,转步骤(7),若不满足,则进入下一步,实施区间分析；

(4)初始化区间分析迭代次数l=0,利用转换关系式,计算pl=h(ek);

(6)判断pl+1是否满足KKT条件,若满足,则令ek+1=h-1(pl+1),进入下一步,若不满足,则令l←l+1,返回步骤(5);

(7)判断是否收敛。若|g(uk+1,ek+1)|≤ε1和‖uk+1-uk‖≤ε2(ε1和ε2为非常小的正常数),则迭代停止,令u*=uk+1,否则,令k←k+1,转步骤(2)。

图3给出了该算法的流程示意图。

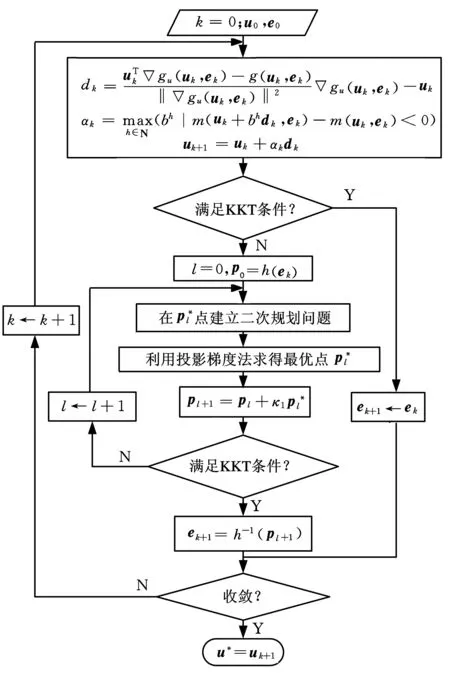
图3　求解Pf max的序列迭代流程

4　算例

在MATLAB下,编写了本文提出的序列迭代算法的可执行程序。为验证本文提出的序列迭代算法的有效性和计算效率，在本节中给出了两个混合型可靠性分析算例。尽管两个算例的极限状态函数均以显式表达式给出，但都编写成了可执行程序,故对于调用函数，极限状态函数是隐式的。采用前向有限差分法计算极限状态函数关于随机变量和区间变量的梯度。

4.1悬臂梁算例

某悬臂梁末端受外部载荷，水平方向分量为Px,垂直方向分量为Py,如图4所示。考虑两种失效模式,当梁承受的最大应力超出材料屈服强度σs，则认为强度失效；当梁末端位移大于末端许用位移D0,则认为刚度失效。极限状态函数分别为

式中,E为材料弹性模量。

图4　悬臂梁示意图

已知臂长L=2000 mm，矩形梁截面的宽度B和高度H均为随机变量,服从正态分布：B～N(55,2)mm,H～N(110,5)mm。材料屈服强度σs=295 MPa,末端许用位移D0=65 mm,材料弹性模量E=210 GPa。载荷分量Px和Py为非独立区间变量,满足负相关关系，令Y=(Y1,Y2)T=(Px,Py)T(单位为N),其椭球模型为

Y∈S=

图5给出了Px和Py满足负相关和独立关系时的不同可行域。

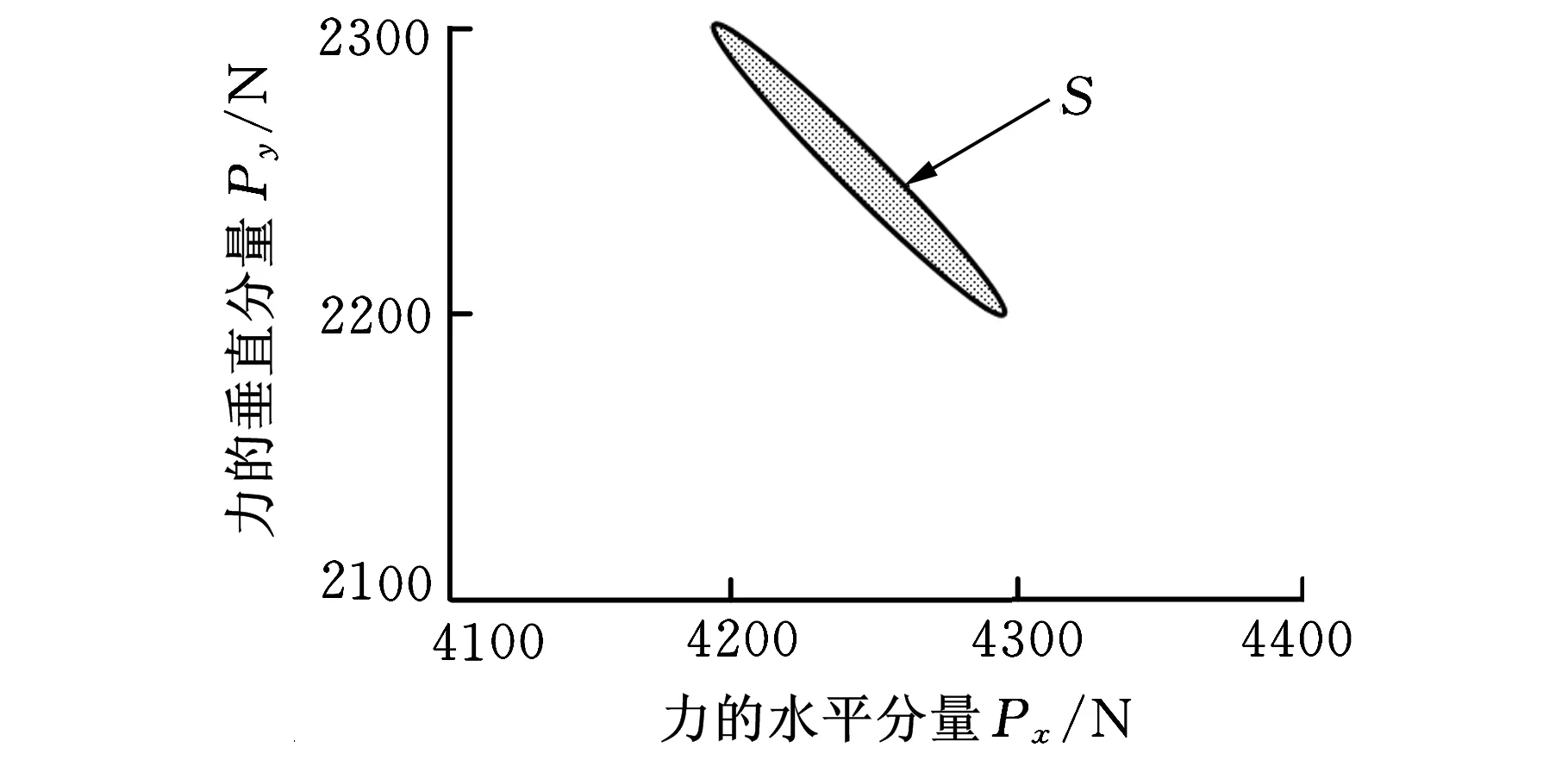
(a)负相关关系

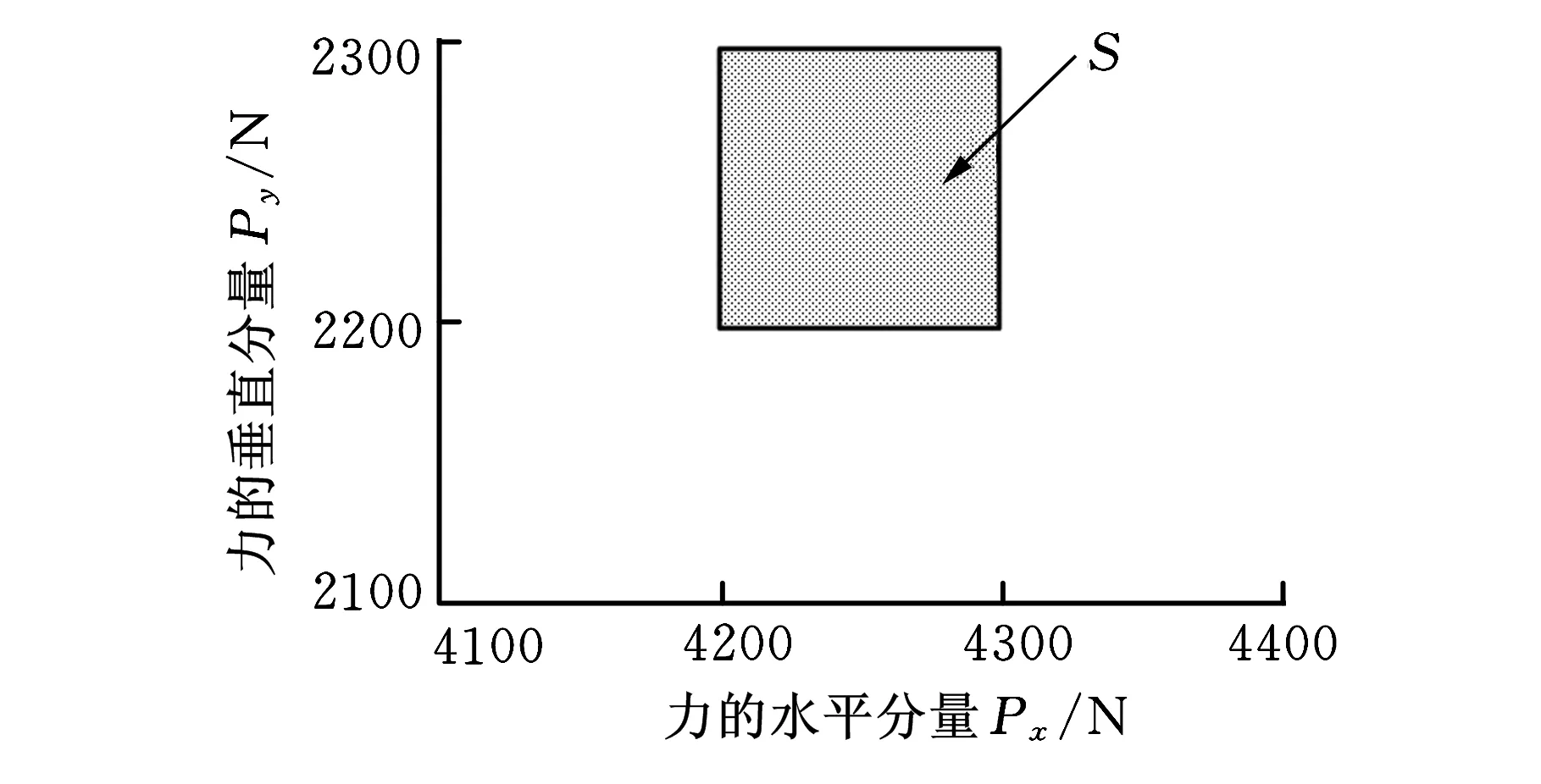
(b)独立关系图5　Px和Py的可行域

表1给出了两种失效工况的最大失效概率,并采用了蒙特卡罗法验证分析结果。为比较计算效率,表1给出了各分析方法调用极限状态函数的次数Nc。同时,表1给出Px和Py假设为独立区间变量时,Px∈[4200,4300]N和Py∈[2200,2300]N两种失效工况的最大失效概率。

由表1可见,本文提出的方法能较高效地求得两种失效模式的最大失效概率。在蒙特卡罗法中，将每个区间变量的可行区间等分为50份,在区间变量的组合值下取随机变量的抽样数为1×106次,则极限状态函数的调用次数为Nc=2.5×108。基于表1给出的蒙特卡罗法结果和相对误差百分比可见，提出的方法具较高的精度。由区间变量满足非独立和独立关系时的分析结果可见，区间变量的独立性对可靠性分析结果的影响较大，假设区间变量独立会导致较保守的分析结果。

表1　两种工况的最大失效概率

4.2悬臂圆筒算例

某悬臂圆筒受外部载荷如图6所示:集中力F1、F2、P和扭矩T。当最大等效von-Mises应力σmax超出材料屈服极限σs,认为悬臂圆筒强度失效,极限状态函数可写为

G=g(X,Y)=σs-σmax

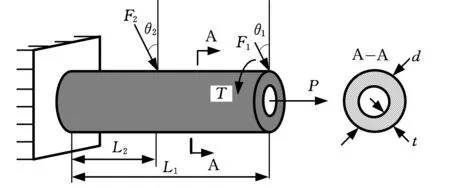
图6　悬臂圆筒

最大等效von-Mises应力位于悬臂圆筒根部截面上端点,其计算式为

其中,σx为该点处的正应力,表达式为

其中,c=d/2,M为该截面处弯矩,A为截面面积,I为截面惯性矩,计算表达式分别为

M=F1L1cosθ1+F2L2cosθ2

τzx为该点的切应力,表达式为

J=2I

表2给出了各随机参数的分布函数及其参数。角度θ1和θ2为独立区间变量(单位：(°))，长度L1和L2为非独立区间变量(单位：mm),满足零相关性。

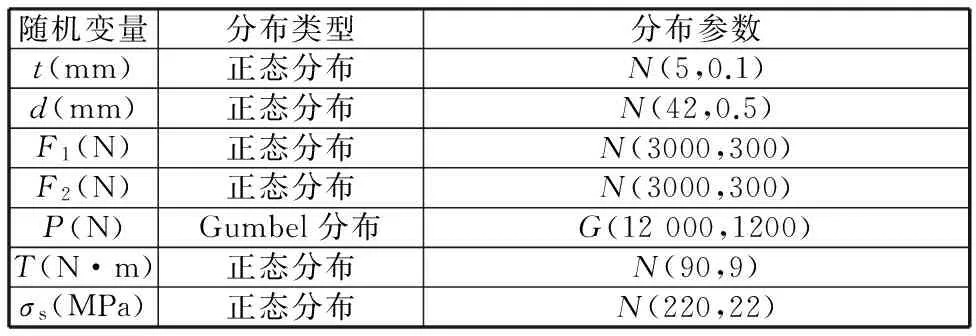
表2　随机变量分布参数

令Y=(Y1,Y2,Y3,Y4)T=(θ1,θ2,L1,L2)T,根据区间变量的独立性特征，将区间变量分为三组,即Ng=3,则Y=(Y1,Y2，Y3)T=(Y1,Y2,(Y3,Y4)T)T,椭球模型为

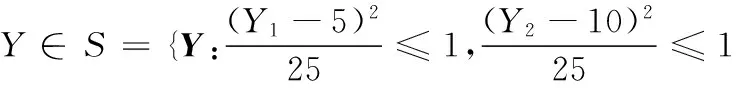
图7给出了L1和L2满足零相关和独立关系时的不同可行域。

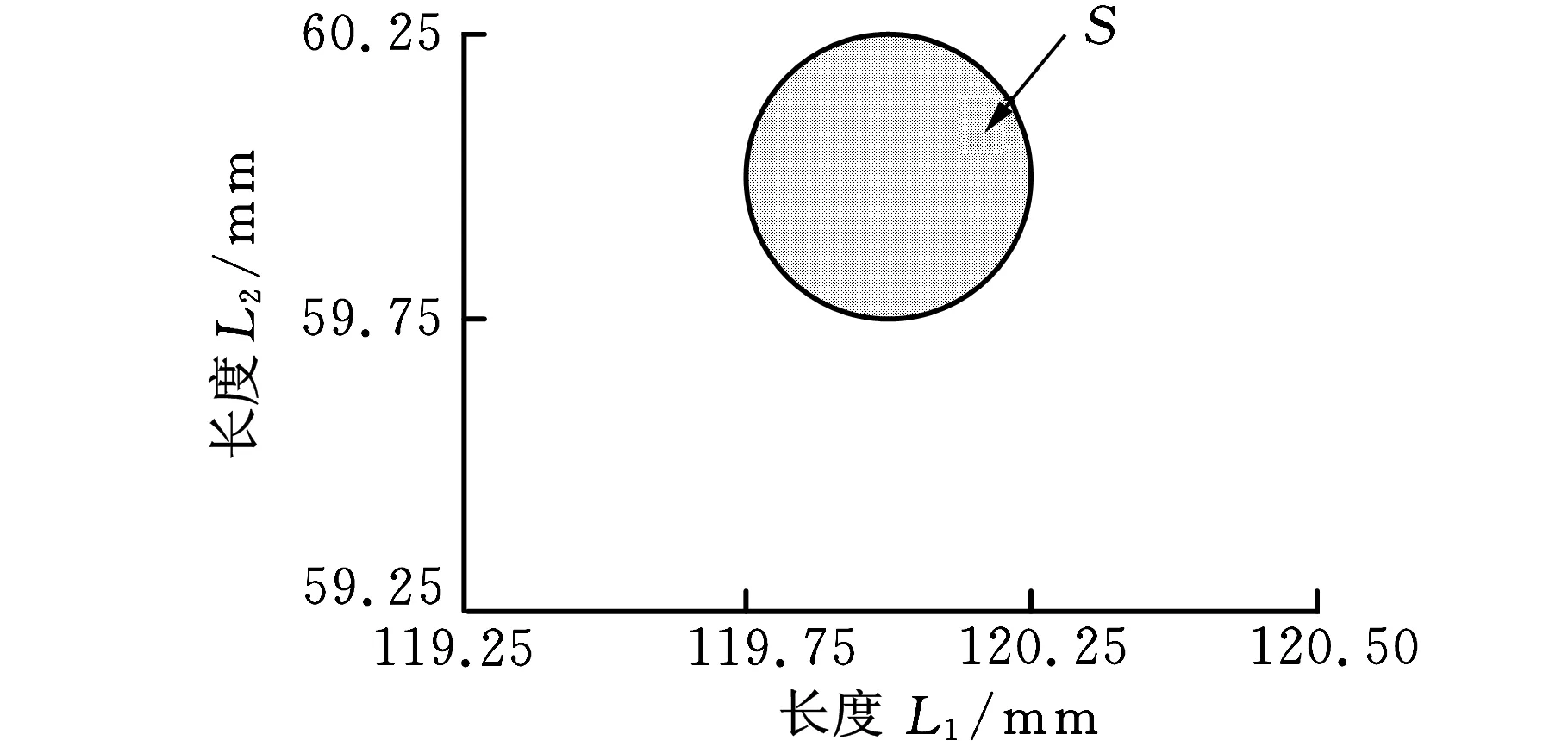
(a)零相关关系

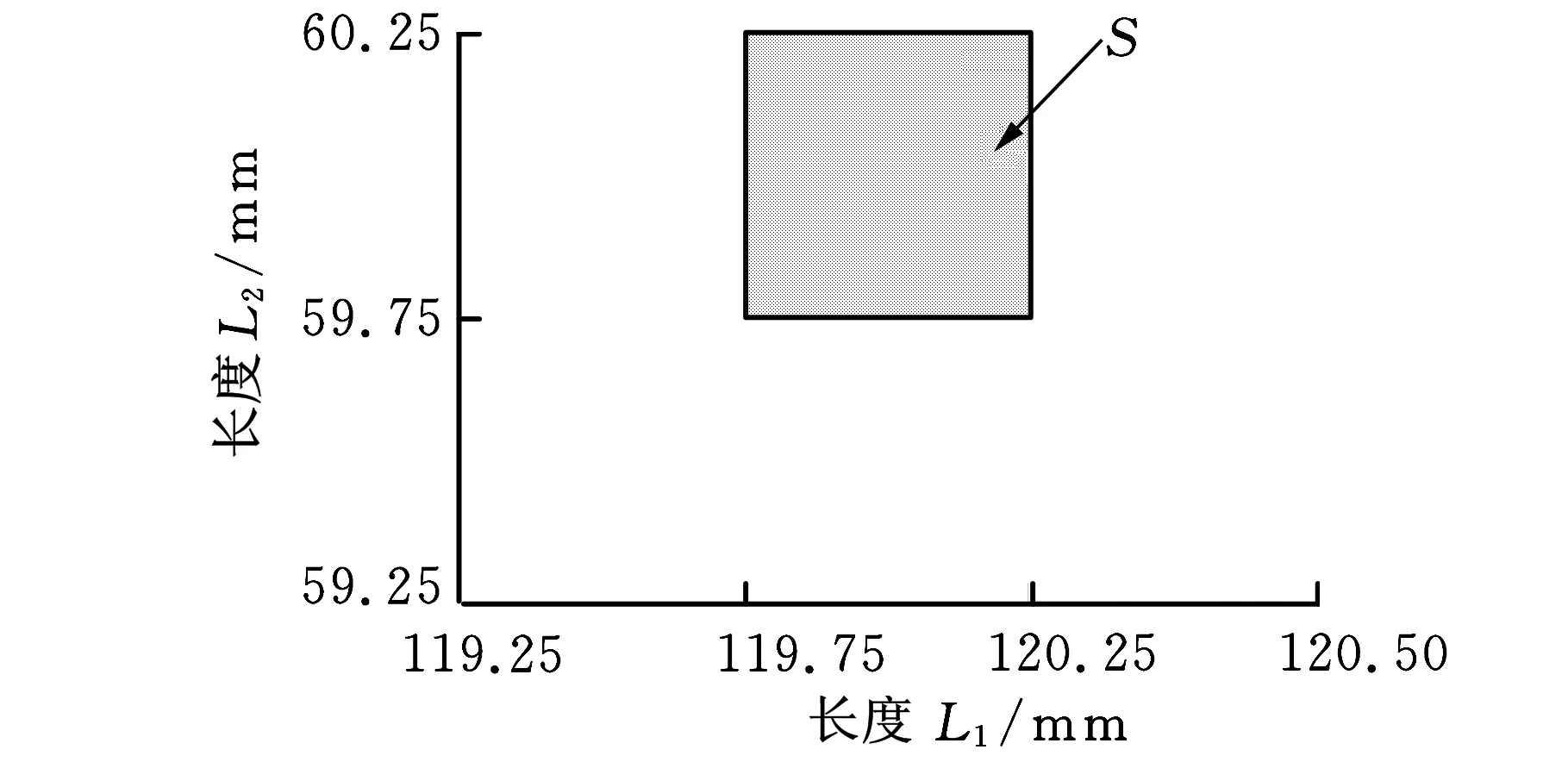
(b)独立关系图7　L1和L2的可行域

表3给出了基于本文提出的方法计算获得的最大失效概率。由表3可见，本文提出的方法能较高效地求得悬臂圆筒的最大失效概率。为验证分析结果的正确性，在蒙特卡罗法中，将每个区间变量的可行区间等分为10份,在区间变量的组合值下取随机变量的抽样数为1×106，则极限状态函数的调用次数为Nc=1.0×1010。基于表3给出的蒙特卡罗法结果和相对误差百分比可见,本文提出的方法具有较高的精度。同样,由区间变量满足非独立和独立关系时的分析结果可见,区间变量的独立性对可靠性分析结果的影响较大，假设区间变量独立会导致较保守的分析结果。

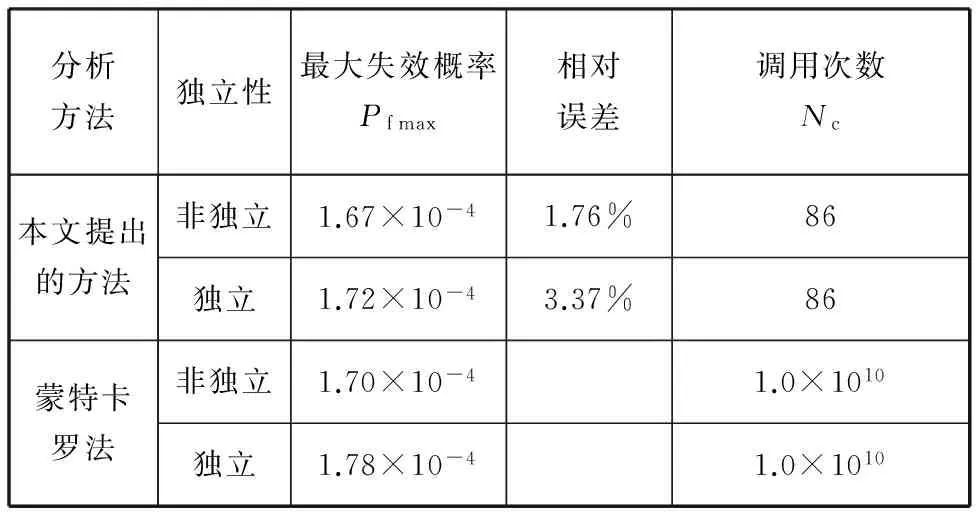
表3　最大失效概率

5　结论

针对机械系统中不确定性输入变量同时存在随机变量和区间变量的情况，考虑非独立性区间变量，基于混合型可靠性分析模型，利用一次二阶矩法，提出了一种可靠性序列迭代算法。算例结果表明：该迭代算法的计算效率较高，计算精度较好；不考虑区间变量的非独立性可产生较保守的可靠性分析结果，可能导致过于保守的可靠性设计结果。

[1]Elishakoff I.Uncertainties in Mechanical Structures:AMF Reudenthal’s Criticisms and Modern Convex Models[J].Journal of Applied Mechanics,1999,63(1):683-692.[2]Nikolaidis E,Ghiocel D M.Singhal S.Engineering Design Reliability Handbook[M].New York:CRC Press,2004.[3]Dubois D,Prade H.A Synthetic View of Belief Revision with Uncertain Inputs in the Framework of Possibility Theory[J].International Journal of Approximate Reasoning,1997,17(2):295-324.

[4]Shafer G.A Mathematical Theory of Evidence[M].Princeton: Princeton University Press,1976.

[5]Yakov B,Elishakoff I.Convex Models of Uncertainty in Applied Mechanics[M].Amsterdam:Elsevier,1990.

[6]Wang P,Youn B D,Xi Z,et al.Bayesian Reliability Analysis with Evolving,Insufficient and Subjective Data Sets[J].Journal of Mechanical Design,2009,131(11):111008.

[7]Moore R E.Methods and Applications of Interval Analysis[M].Philadelphia:Siam,1979.

[8]Du X,Sudjianto A,Huang B.Reliability-based Design with the Mixture of Random and Interval Variables[J].Journal of Mechanical Design,2005,127:1068.

[9]江涛,陈建军,姜培刚,等.区间模型非概率可靠性指标的一维优化算法[J].工程力学,2007,24(7):23-27.

Jiang Tao,Chen Jianjun,Jiang Peigang,et al.A One-dimensional Optimization Algorithm for Non-probabilstic Reliability Index[J].Engineering Mechanics,2007,24(7):23-27.

[10]姜潮,黄新萍, 韩旭,等.含区间不确定性的结构时变可靠度分析方法[J].机械工程学报,2013,49(10):186-193.

Jiang Chao,Huang Xinping,Han Xu,et al.Time-dependent Structural Reliability Analysis Method with Interval Uncertainty[J].Journal of Mechanical Engineering,2013,49(10):186-193.

[11]Du X.Unified Uncertainty Analysis by the First Order Reliability Method[J].Journal of Mechanical Design,2008,130(9):091401.

[12]Jiang C,Han X,Liu G P.A Sequential Nonlinear Interval Number Programming Method for Uncertain Structures[J].Computer Methods in Applied Mechanics and Engineering,2008,197(49/50):4250-4265.

[13]Du X.Reliability-based Design Optimization with Dependent Interval Variables[J].International Journal for Numerical Methods in Engineering,2012,91(2):218-228.

[14]Jiang C,Zhang Z,Zhang Q,et al.A New Nonlinear Interval Programming Method for Uncertain Problems with Dependent Interval Variables[J].European Journal of Operational Research,2014,238(1):245-253.

[15]Ben-Haim Y.Convex Models of Uncertainty:Applications and Implications[J].Erkenntnis,1994,41(2):139-156.

[16]Kreinovich V,Beck J,Nguyen H T.Ellipsoids and Ellipsoid-shaped Fuzzy Sets as Natural Multi-variate Generalization of Intervals and Fuzzy Numbers: How to Elicit Them from Users, and Howto Use Them in Data Processing[J].Information Sciences,2007,177(2):388-407.

[17]Kreinovich V,Hajagos J G,Tucker W T,et al.Propagating Uncertainty through a Quadratic Response Surface Model[R].Albuquerque,New Mexico:Sandia National Laboratories,2008.

[18]Zhang Y,Kiureghian A.Two Improved Algorithms for Reliability Analysis[C]//Proceedings of the Sixth IFIP WG7.5 Working Conference on Reliability and Optimization of Structural Systems.Springer US,1995:297-304.

[19]Nocedal J,Wright S.Numerical Optimization[M].New York:Springer,2006.

(编辑卢湘帆)

A Sequential Iteration Algorithm for Reliability Analysis with Random and Dependent Interval Variables

Pan Baisong1Xie Shaojun1Du Xiaoping2Liang Lihua1

1.Zhejiang University of Technology,Hangzhou,310014 2.Missouri University of Science and Technology,Rolla,USA

Focusing on the mixed conditions of both random variables and dependent interval variables,an efficient hybrid reliability analysis method was proposed.Interval variables made the reliability analysis problem become a double-loop optimization problem.In order to reduce the impacts on the reliability analysis efficiency by the double-loop optimization and dependent interval variables, an efficient sequentially iterative strategy was proposed,and a formula to transform the dependent interval variables modelled by ellipsoid model was developed into independent interval variables,and the limit-state function was approximated during the inner loop in the second order form to make the optimization problem become a more solvable quadratic programming problem.The results show that the proposed sequential iteration algorithm has good efficiency and accuracy, and that the reliability analysis results are affected by the assumption of dependence between interval variables; results under the assumption of independence between interval variables can be more conservative than that of dependence.

reliability analysis;ellipsoid model;dependent interval variable;sequentially iterative algorithm

2015-01-14

国家自然科学基金资助项目(51475425,51075365)

TH122DOI：10.3969/j.issn.1004-132X.2015.12.002

潘柏松,男,1968年生。浙江工业大学机械工程学院教授、博士研究生导师。主要研究方向为可靠性设计、可靠性工程、现代设计方法。出版专著1部,发表论文40余篇。谢少军,男,1986年生。浙江工业大学机械工程学院博士研究生。Du Xiaoping，男，1963年生。美国密苏里科技大学机械和航空航天工程系教授、博士研究生导师。梁利华，男，1973年生。浙江工业大学机械工程学院教授、博士研究生导师。