RZS盘式制动器制动倍率的研究(续)

夏德茂　奚　鹰　华滨滨　朱文翔

同济大学,上海,201804

RZS盘式制动器制动倍率的研究(续)

夏德茂奚鹰华滨滨朱文翔

同济大学,上海,201804

依据RZS盘式制动器的工作原理，建立了其机构运动简图；计算和比较了该机构在有无制动盘情况下的自由度；考虑闸调机构伸长量的影响，研究了该制动器在闸片间隙等于设定值和闸片间隙补偿后制动倍率的变化情况。研究结果表明：RZS盘式制动器的制动倍率符合工程设计要求；闸调机构的伸长量与闸片磨损量存在线性变化关系；在闸片的整个服役周期内，制动倍率几乎不变。

盘式制动器；制动倍率；闸片间隙；闸调机构；磨损

0　引言

RZS盘式制动器是由德国克诺尔公司研发的新型基础制动装置,其作用是将空气压缩力放大适当倍数后平均传递至各闸片，将其转变为压紧制动盘的机械力，并借助盘片间产生的摩擦阻力来阻止车轮转动[1-4]。基础制动装置的制动倍率是衡量列车制动性能的一个重要指标，其大小直接影响盘片之间的正压力，进而影响制动摩擦力矩的大小，决定列车能否在规定的距离内实现停车制动[5-6]。饶忠[7]详细阐明了踏面制动器制动倍率的计算过程，认为制动倍率为制动梁数、制动缸杠杆倍率和转向架杠杆倍率的乘积，一般在6～9之间，且该数值仅有双侧踏面制动器才能达到。盘式制动器的工作原理虽与踏面制动器一致，但两者在结构上差别很大，故制动倍率的计算方法也不尽相同。

笔者前期对该制动器间隙补偿前后的制动倍率进行了分析和计算[5]，但在后续研究中发现，在制动倍率(即正压力N与空气压缩力F两者关系)的推导过程中，无需将闸调机构看成是二力杆,也不需要假设空气压缩力F始终垂直于中心线，此外，文献[5]未考虑闸片间隙补偿后闸调机构的伸长量带来的影响，因此,本文在文献[5]研究的基础上，考虑以上因素，对RZS盘式制动器的制动倍率进行更深入的研究。

1　RZS盘式制动器的工作原理

RZS盘式制动器几种常用工况的详细工作原理见文献[5]。为绘制该机构的运动简图，本文仅简单介绍常用工作制动工况的工作原理。图1为该制动器的结构示意图，该制动器主要由制动夹钳、闸瓦托、偏心轴、弹簧储能停放制动气缸、隔膜式工作制动气缸、闸片间隙自动调整机构(简称闸调机构)、紧急手动释放装置等零部件组成。

图1　RZS盘式制动器结构示意图

当经判断需要施加空气制动时，隔膜式工作制动气缸内的推盘活塞在空气压缩力的作用下按箭头方向运动，与偏心轴通过螺栓固接在一起的拨叉及偏心轴在推盘活塞的作用下顺时针转动，进而带动套装于偏心轴头上的制动夹钳向一侧运动。闸片间隙自动调整装置按图1所示箭头方向运动，带动另外一侧的制动夹钳绕固定铰点逆时针转动，进而两侧闸片(图1未示出)抱紧制动盘,产生制动力。当闸片间隙等于设定值时，制动过程中，闸调机构相当于一刚性块。当闸片间隙大于设定值时或制动过程中发生磨损后，通过增加推盘活塞的行程，带动闸调机构伸长，闸片间隙得到补偿，使得在下一次制动前，闸片间隙仍等于设定值。

2　RZS盘式制动器数学模型

依据RZS盘式制动器的工作原理，可绘制出图2所示初始状态下的机构运动简图。其中,A、O1、O2、B、C、D、E为铰点。O1为偏心轴的固定旋转中心,O2为偏心轴上的偏心铰点,D为固定铰点。P为空气压缩力F的作用点。a、b分别为制动夹钳ED(AO2)和DC(O2B)的长度。c为闸调机构BC的初始长度,c可变。e为偏心轴O1O2的距离，即偏心距。α1、α2分别为制动夹钳EDC(AO2B)的夹角和DC(O2B)与X轴的夹角。θ1为O1O2连线与X轴的夹角。 g为固定铰点D和偏心点O2至中心线的距离。h为偏心轴固定旋转中心O1至中心线的距离。k为铰点A和E至摩擦面的垂直距离。l为制动盘的厚度。f1和f2为两侧的闸片间隙。偏心轴总成3为原动件，由于制动缸本体结构设计的限制，偏心轴总成3转过的最大角度为2θ1。XY为全局坐标系，X′Y′为局部坐标系。

1、6.闸片　2、5.制动夹钳　3.偏心轴总成　4.闸片间隙自动调整装置　7.制动盘图2　RZS盘式制动器机构运动简图

如图2所示,该制动器包含6个活动构件,共有6个转动副、1个移动副和1个虚约束。因此,其自由度T为

T=3n-2p1-p2=3×5-2×7=1

式中,n为活动构件数；p1为低副数；p2为高副数。

若不考虑制动盘，其自由度为

T=3n-2p1-p2=3×4-2×5=2

(1)

式(1)表明,该制动器在未装备于列车上时，自由度为2，大于原动件数目1，表明该机构没有明确的运动。需指出的是，即使存在制动盘7，在任意一侧的闸片未贴着制动盘之前，该机构的自由度仍为2。依据RZS盘式制动器的结构设计，在未工作时和每次制动结束后，偏心轴在推盘复位弹簧力的作用下，其偏心点O2始终要与固定铰点D关于中心线对称，如图2所示，而夹钳EDC和AO2B又具有相同的结构特征,因此,本文在绘制机构运动简图时，假设闸调机构BC两点也关于中心线对称。若参数a、b、l、k、g、α1和闸调机构BC的初始长度c均已知，则该制动器的闸片间隙设定值f和两侧的闸片间隙f1、f2须满足：

f=f1=f2=

[2bsinα2+c-l-2k-2asin(α1+α2)]/2

(2)

若不假设闸调机构BC关于中心线对称，则两侧的闸片间隙f1和f2须满足：

f1+f2=2bsinα2+c-l-2k-2asin(α1+α2)

(3)

式(3)表明，f1和f2可为任意值，但两者之和须满足式(3)。为简化制动倍率的推导，本文以式(2)为前提对该制动器的制动倍率进行研究。

3　制动倍率i的计算

与文献[5]一致，本文仍对RZS单元制动器在闸片间隙等于设定值时和闸片间隙发生补偿后两种情况下的制动倍率分别进行研究。

3.1闸片间隙等于设定值时

当两侧闸片间隙等于设定值f时,若已知P点在局部坐标系X′Y′的坐标为(m,n),则初始状态下,各铰点(O1、O2、P、A、B、C、D、E)在XY坐标系中的位置坐标分别为

xO1=0,yO1=0

xO2=-ecosθ1,yO2=-esinθ1

xP=mcosθ1-nsinθ1,yP=msinθ1+ncosθ1

xA=-ecosθ1+acos(α1+α2)

yA=-esinθ1+asin(α1+α2)

xB=-ecosθ1+bcosα2,yB=-esinθ1+bsinα2

xC=-ecosθ1+bcosα2,yC=g+h-bsinα2

xD=-ecosθ1,yD=g+h

xE=-ecosθ1+acos(α1+α2)

yE=g+h-asin(α1+α2)

θ1=arcsin((g-h)/e)

制动发生时,在空气压缩力F的作用下,假定偏心轴总成3绕固定旋转中心O1转过的角度为Δθ1,夹钳EDC绕固定铰点D逆时针转过的角度为Δα2,两侧的闸片贴紧制动盘,在摩擦面上产生正压力N,如图3所示。

图3　制动发生后各铰点的位置示意图

xE′=-ecosθ1+acos(Δα2-α1-α2)

yE′=-esinθ1+asin(Δα2-α1-α2)

xC′=-ecosθ1+bcos(Δα2-α2)

yC′=g+h+bsin(Δα2-α2)

xA′=-ecos(θ1-Δθ1)-

yA′=-esinθ1+asin(α1+α2)+f

f=-asin(α1+α2)-asin(Δα2-α1-α2)

由于两侧的闸片间隙值等于初始设定值,闸调机构BC在制动发生时相当于一刚性块,初始长度c不会发生改变,故偏心轴总成3转过的角度Δθ1可通过下式求出：

|B′C′|=c

(4)

从图3中可以看出,RZS单元制动器制动倍率的计算公式为

i=2N/F

(5)

式中,i为制动倍率;闸片数目为2。

已知各参数数值如下：a=220 mm,b=252 mm,c=175 mm,e=12.5 mm,g=130 mm,h=127 mm,k=70 mm,l=35 mm,m=100 mm,n=6 mm,α1=3.013。将以上参数代入式(2)可得到闸片间隙设定值f及初始闸片间隙f1和f2:

f1=f2=f=1.5 mm

代入式(4)可得到偏心轴转过的角度Δθ1:

Δθ1=0.1295 rad

因此,可称Δθ1为闸片间隙设定值f对应的偏心轴旋转角度设定值。

为得到式(5)中正压力N与空气压缩力F之间的关系,可依据静力学知识,采用逆推方法分别对制动夹钳EDC、闸调机构BC、制动夹钳AO2C及偏心轴总成PO1O2进行受力分析,最终得到制动倍率i值：

i=2N/F=8.638

若引入机械传递效率η,当理论制动倍率i确定后,便可得到实际制动过程中,盘片之间的正压力2N与空气压缩力F的关系式：

2N=Fiη=(pS-Fk)iη

式中,p为工作压力,MPa;Fk为推盘活塞复位弹簧力,约为500 N;S为推盘活塞面积,cm2;η为效率,取0.97。

图4所示为正压力2N随工作压力p的变化曲线。在RZS盘式制动器的结构设计中，可通过改变推盘活塞的底面积S来满足不同列车对不同制动性能的要求,使得该制动器的应用范围更加广泛。在正常工作压力380 kPa下,不同的S(142.7 cm2、131.6 cm2、122 cm2)对应的制动力分别达到41 kN、37 kN、34 kN。随着工作压力的继续增大,该制动器的最大制动力能达到60 kN。

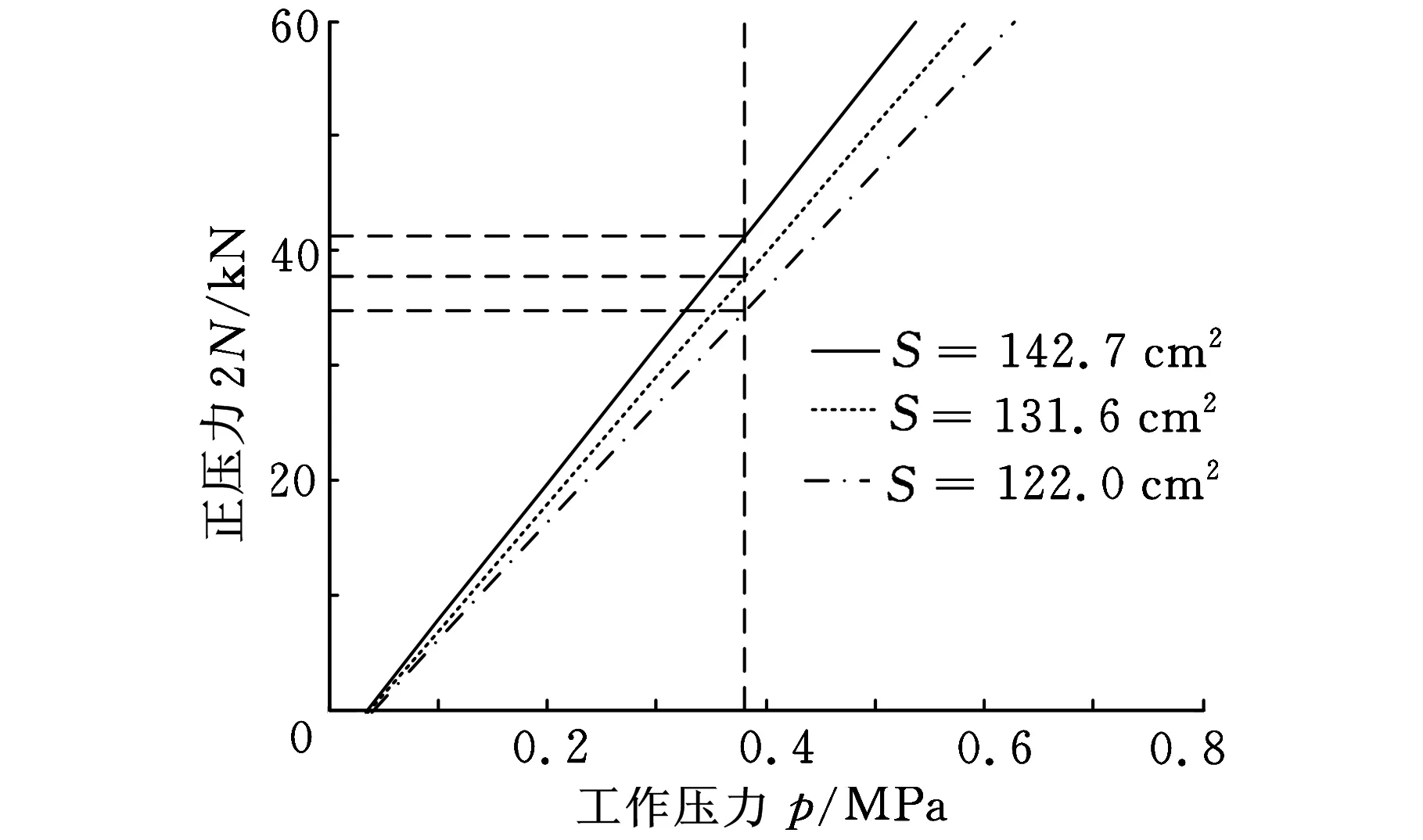
图4　正压力2 N与工作压力p的关系

3.2闸片间隙补偿后

在制动过程中,摩擦面势必要发生磨损,且磨损量随制动次数的增加而增加。依据RZS单元制动器的工作原理，每次制动过程中发生的磨损量可增加推盘活塞的行程即偏心轴转过的角度来保证闸片始终贴紧制动盘，且会在制动结束前的瞬间，通过闸调机构BC的伸长进行补偿，确保下一次制动开始前，闸片间隙仍等于设定值。间隙补偿后,图2中BC两点间的距离不再是初始值c=175 mm,且随着磨损量的增大,BC长度会不断增大。因此,有必要研究闸片间隙发生补偿后制动倍率的变化情况。假定单次制动过程中的磨损量Δf全部在闸片上,且每次磨损量均相等，即闸片摩擦面至点E、A的距离由k变为k-Δf,如图5所示。此时,O1O2连线与X轴的夹角仍为θ1,闸片间隙仍为设定值f,但BC的长度为c′,设其增量为Δc。整个机构仍关于中心线对称,假设此时连线DC和O2B与X轴的夹角为ε1。

图5　制动补偿后各铰点的初始位置示意图

间隙补偿后,下一次制动发生前，在初始位置下,各铰点A、B、C、E在全局坐标系XY中的位置坐标分别为

xA=-ecosθ1+acos(α1+ε1)

yA=-esinθ1+asin(α1+ε1)

xB=-ecosθ1+bcosε1,yB=-esinθ1+bsinε1

xC=-ecosθ1+bcosε1,yC=g+h-bsinε1

xE=-ecosθ1+acos(α1+ε1)

yE=g+h-asin(α1+ε1)

(6)

2Δf=2k+2f+l-c′+2asin(α1+ε1)-2bsinε1

(7)

将式(6)代入式(7)便可得到闸调机构BC长度的增量Δc与磨损量Δf的变化关系，如图6所示,可以看出，闸调机构BC的增量Δc随磨损量Δf呈线性增大的变化规律。两者的变化关系可用下式近似表示：

Δc≈2.2Δf

(8)

图6　Δc随Δf的变化曲线

xE′=-ecosθ1+acos(Δα2-α1-ε1)

yE′=-esinθ1+asin(Δα2-α1-ε1)

xC′=xD′+bcos(Δα2-α2),yC′=yD+bsin(Δα2-α2)

xA′=-ecos(θ1-Δθ1)-

yA′=-esinθ1+asin(α1+ε1)+f

f=-asin(α1+ε1)-asin(Δα2-α1-ε1)

此时,偏心轴转过的角度Δθ1可由下式求出：

|B′C′|=c′=c+Δc

可按照3.1节的方法依次对各零件进行静力学分析,最终得到制动倍率i。图7所示为单次闸片间隙磨损量Δf与制动倍率i的关系曲线。

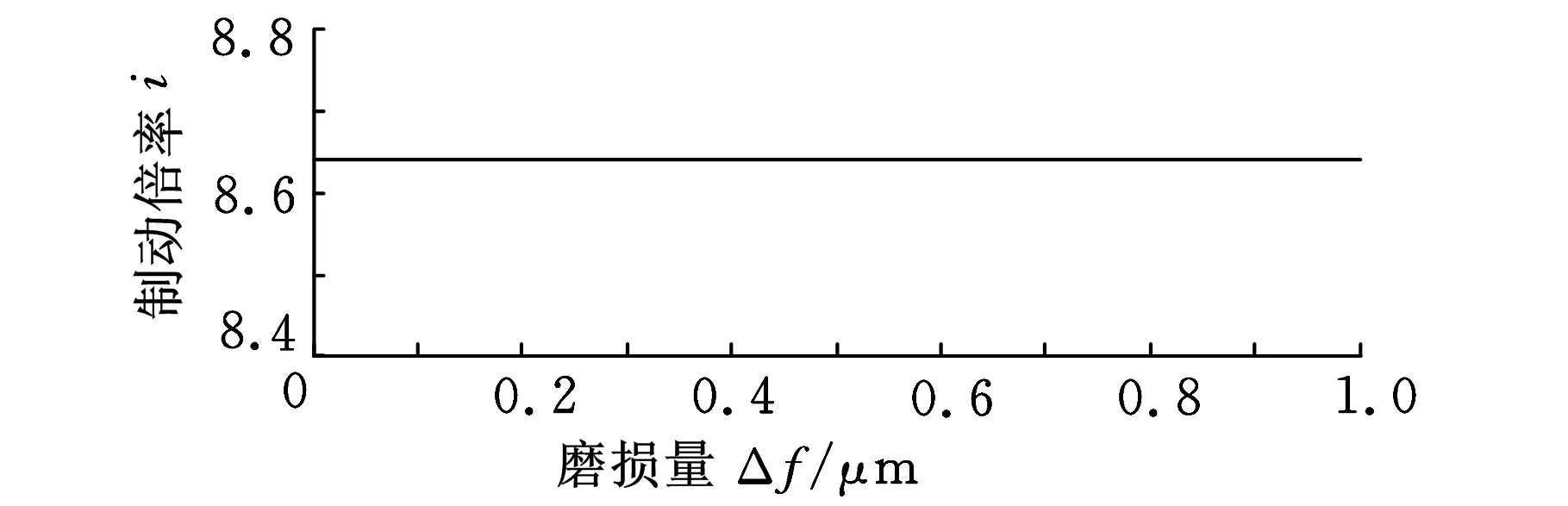
图7　制动倍率i随Δf的变化曲线

从图7中可以看出,在单次制动过程中,若增加制动过程中的单次磨损量，制动倍率i几乎不变。这是因为在一次制动过程中，闸片的磨损量Δf很小,为微米级，故不难判断制动倍率i的变化趋势为一条水平直线。

随着制动次数的增加，闸片的磨损量不断增大,即k值不断减小，当达到极限值时，便需要更换闸片。但在闸片的整个服役周期内，制动倍率i的变化值得研究。闸片k值由35 mm减小至30 mm时,偏心轴在闸片间隙补偿后,下一次制动过程中转过的角度Δθ1和制动倍率i的变化曲线,如图8所示。

从图8中可以看出,随着制动次数的增加,制动倍率i呈线性增大,从最初零磨损量(新闸片)时的8.638变化至磨损量为5 mm时的8.6495。偏心轴总成转过的角度Δθ1由最初的零磨损量(即f=1.5 mm)下的设定值0.1295增大至发生5 mm磨损时的0.1297,图8中Δθ1直线的波动主要是因为计算中使用式(8)中Δc与Δf的近似线性关系。制动倍率i的变化量仅为0.0115，Δθ1的变化量仅为0.0002,两者几乎不变。因此，在闸片的整个服役周期内,RZS盘式制动器的制动倍率始终能保持在某一固定值左右，几乎不会引起制动力发生改变。每次制动时，由于闸片间隙调整装置的无极补偿作用，制动过程中偏心轴的旋转角度不变，始终为闸片间隙设定值f对应的0.1295。上述结论也是工程设计人员在研发新型铁路车辆基础制动装置过程中值得关注的问题之一。

图8　i和Δθ1随k的变化曲线

4　结论

(1)制动倍率在整个闸片的服役周期内基本不变,保证了每次制动过程中闸片和制动盘之间制动力的稳定性，这对配合摩擦副的设计起着关键作用。若制动倍率发生变化或变化很大，可能导致原先设计的摩擦副的强度因制动力的增大而发生结构性破坏，进而发生制动失效。

(2)在制动过程中,虽然在闸片摩擦面上发生的磨损可通过增加偏心轴的行程来促使闸片间隙调整机构在制动结束前对其进行补偿，但是下一次制动发生时，偏心轴仍要转过相同的角度。因此，可认为该角度为闸调机构发生间隙补偿作用的一个临界判断值。当偏心轴转过角度大于此数值时，无论是空载(无制动盘)还是制动过程中发生的磨损，在一系列力传递机构的作用下，闸调机构都要伸长。

[1]丁勇.列车运行计算与设计[M].北京:北京交通大学出版社,2011.

[2]张振淼.城市轨道交通车辆[M].北京:中国铁道出版社,2011.

[3]应云飞,秦娟兰.城市轨道交通车辆制动系统[M].成都：西南交通大学出版社，2011.

[4]夏德茂，奚鹰，李涛，等.广州地铁3号线基础制动装置及制动距离研究[J].城市轨道交通研究,2014(2):101-105.

XiaDemao,XiYing,LiTao,etal.StudyontheFundamentalBrakingDeviceandBrakingDistanceofGuangzhouMetroLine3[J].UrbanMassTransit,2014(2):101-105.

[5]夏德茂，奚鹰，李涛，等.RZS盘式制动器制动倍率的研究[J].中国机械工程，2014，25(8)：1131-1135.

XiaDemao,XiYing,LiTao,etal.StudyonBrakingRateofDiscBrakeUnitRZS[J].ChinaMechanicalEngineering,2014,25(8):1131-1135.

[6]应云飞，秦娟兰. 城市轨道交通车辆制动系统[M].成都：西南交通大学出版社,2011.

[7]饶忠.列车制动[M].北京：中国铁道出版社,2011.

(编辑陈勇)

Study on Braking Rate of Disc Brake Unit RZS(Continue)

Xia DemaoXi YingHua BinbinZhu Wenxiang

Tongji University,Shanghai,201804

Firstly,according to the working principles of the braking unit RZS,the kinematic diagram was built up.Then,the DOF of RZS with and without the brake disc was analyzed and compared.The braking rate and its change rules were calculated and analyzed respectively under two conditions:the pad clearance was equal to the setting value and another the pad clearance was reset after braking operation.It is found that:the braking rate of RZS meets the design requirements and there is a linear relationship between the increment of the self-adjustment mechanism and the amount of the pad’s wear.During the entire service life of the pad, the braking rate of RZS barely changes.

disk brake unit;braking rate;pad clearance;self-adjustment mechanism;wear

2014-12-25

国家自然科学基金资助项目(61004077)

U231DOI：10.3969/j.issn.1004-132X.2015.16.020

夏德茂,男,1986年生。同济大学机械与能源工程学院博士研究生。主要研究方向为铁路车辆制动设备及其关键技术。发表论文16篇。奚鹰,男,1957年生。同济大学机械与能源工程学院教授、博士研究生导师。华滨滨,男,1991年生。同济大学机械与能源工学院硕士研究生。朱文翔,男,1991年生。同济大学机械与能源工程学院硕士研究生。