广义BOM时间建模

闫崇京

南京航空航天大学,南京,210016

广义BOM时间建模

闫崇京

南京航空航天大学,南京,210016

针对广义BOM建模中的时间模糊性和约束多样性问题，提出了BOM时间的多色图描述方法。采用模糊数表达BOM时间，通过图的“着色”实现多种时间约束的表达；建立了BOM时间到时间约束网络的映射规则，给出了BOM时间一致性的判定和求解方法；最后通过实例对BOM时间模型及其求解方法进行了验证。

BOM；时间约束网络；模糊时间；生产计划

0　引言

飞机、舰船等大型复杂装备具有构型变化和历史状态变化多而复杂的特点,产品生命周期中的数据一致性很难保证。基于单一产品数据源的思想,波音公司构建了DCAC/MRM系统,空客公司随后跟进了该技术的研究。国内对单一产品数据源技术也展开了相关研究，文献[1]提出一种单一企业物料清单，提高了信息共享的效率；文献[2]提出主-子模型的集成模型， 基于历史状态驱动模型变化,解决了构型管理的问题。扩展型物料清单[3]、制造过程语义模型[4]等则通过BOM语义的扩展以提升对制造过程的描述能力。现有研究给出了解决BOM一致性的思路和方法，但仍采用传统的时间表达方法,如文献[1]中的计划开工日期、计划完工日期、实际开工日期、实际完工日期。工程实际中,由于信息量的不足,BOM时间具有模糊性[5]，仅能给出一个可能的时间范围。此外,现有方法难以区分不同的时间约束类型,增加了计算机求解难度。本文针对BOM时间的模糊性和时间约束的多样性，提出一种BOM时间的多色图模型，并给出基于时间约束网络的求解方法。

1　BOM时间模型

1.1BOM时间参数选择

BOM模型往往会给出BOM节点(制造活动)的基本运行时间，以满足各级生产计划编制的需要。传统方法中，制造活动的运行时间为确定值，在此基础上，可以计算物料需求的提前期、制造活动的开工日期和完工日期、项目的总工期等时间参数。BOM建模时，由于许多工作缺少经验，或者任务信息难以获取,从而使得活动运行时间存在随机性、不知性和模糊性，制造活动运行时间的不确定性通常是这三者的综合反映[6]。由于制造活动运行时间的不确定性并不是其本身信息的不确定性，而是工程人员对该不确定性信息的主观反映，因此，采用模糊数学表达制造活动运行时间更为合理。一般地,定义制造活动运行时间为三角模糊数：

(1)

式中,dmin、dmst、dmax分别为最短运行时间、最可能运行时间和最长运行时间。

BOM时间参数同时包含了时间点和时间区间两种类型,如制造活动的开始时间和结束时间为时间点,而活动的运行时间、活动开始时间范围为时间区间。因此，在建模和计算过程中需要区别对待。BOM中除了制造活动运行时间外，还需要描述活动之间的约束关系。根据Allen的时间区间代数，对其13种关系进行整理可以得到BOM中两个制造活动之间的4种约束关系:开始-开始时间约束(start-to-start,STS)、开始-结束时间约束(start-to-finish,STF)、结束-开始时间约束(finish-to-start,FTS)和结束-结束时间约束(finish-to-finish,FTF)，如图1所示。

图1　BOM时间约束

在BOM中需要表达制造活动运行时间和4种时间约束。4种时间约束可采用式(1)描述，而活动运行时间可以转换为STF时间约束，则BOM中的时间参数为4种时间约束，隶属度函数统一表达为

式中,dcs,min、dcs,mst、dcs,max分别为最短时间约束、最可能时间约束和最长时间约束。

1.2BOM模糊时间模型

定义1BOM时间模型是一个多色图:

BOM=(ACTIVITY,LINK,TIME)

其中,ACTIVITY=A={ai|i=1，2,…，n}是BOM节点的集合,表示制造活动,i为节点序号。LINK={L,F,L×F}为BOM联系的多色集合,L={〈ai,aj〉|i,j=1,2,…,n}是BOM联系的集合,表示制造活动之间的关联关系；F={logical，Ⅰ，Ⅱ，Ⅲ，Ⅳ}是联系的“颜色”，表示关联关系的属性：逻辑联系logical、Ⅰ类时间约束、Ⅱ类时间约束、Ⅲ类时间约束和Ⅳ类时间约束；L×F表示边的“着色”,即确定联系的类型。关联关系的属性之间为“或取”关系，即一个关联关系可以同时具有多种属性，或者没有属性，任意一联系的属性表达为F(l)=F1(L)∨F2(L)∨F3(L)∨F4(L)∨F5(L),l∈L。TIME={D,L×D]}是BOM时间约束的多色集合,D={〈dcs,min,i,j,dcs,mst,i,j,dcs,max,i,j〉|i,j=1,2,…,m}是时间约束集合,i,j为节点序号。

2　BOM时间网络

2.1BOM时间网络模型

时间约束网络能较好地描述时间知识和时间约束，并采用图论方法对约束满足问题进行推理和求解。相较于模糊时间BOM的普通求解方法，时间约束网络在求解时间参数的同时,实现了BOM时间约束的冲突检测。

定理1BOM时间是一致的,当且仅当对应的BOM时间约束网络GT中不存在负环。

2.2BOM模型变换

令λ为模糊时间隶属度函数的截集阈值。

规则2若F2(li,j)∨F3(li,j)∨F4(li,j)∨F5(li,j)=1,有以下四种情况：

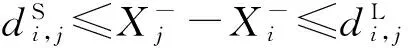
i,j=1,2,…,n

规则4若F1(li,j)∨F2(li,j)∨F3(li,j)∨F4(li,j)∨F5(li,j)=0,则有

定义DT为BOM最小时间距离矩阵,di,j为活动节点i到活动节点j的最小时间距离。DT的求解是图论中的最短距离问题，选择算法时需考虑图中的负环。若di,j≥0,则BOM时间约束是一致的,且

式中,tS i、tF i分别为i节点的开始时间和结束时间。

若di,j<0,则BOM时间约束存在冲突。此时,需松弛相关时间约束,最小松弛量为

3　应用实例

某大型装备部件A的基本结构和时间约束如图2所示,其BOM时间模型为

A={0010,1001,1002,1003,2001,2002}

图2　BOM模糊时间模型实例

对图2所示的BOM映射后得到图3所示的时间约束网络，其中,S0、F0分别为总开始节点和总终止节点；内部节点中，S表示开始节点，F表示结束节点，如S1001为BOM中1001对应的开始节点，F1002为BOM中1002对应的结束节点。根据规则1得到时间约束网络。

图3　BOM时间约束网络

基于Floyd-Warshall算法[7]求解该BOM时间约束网络：

float Dis[n][n];//BOM时间约束网络

for( int k = 1; k〈n; k + + )

for( int i = 1; i〈n; i + + )

for( int j = 1; j〈n; j + + )

Dis[i][j] = min ( Dis[i][j]，Dis[i][k] + Dis[k][j])

λ=0.8时的时间约束矩阵为

矩阵中空白处的元素为0;dS1001,S1001、dF1001,F1001、dS1002,S1002、dF1002,F1002、dS010,S0010、dF010,F0010均小于0,即时间约束网络中存在负环,由定理2可知BOM中的时间约束存在冲突。由式(3)逐步调整,并使BOM汇点协调时差为0,有

调整后的矩阵中无负环。因此,可得λ=0.8时的制造活动的时间范围；同理，可求出λ=0.9时BOM中各制造活动的时间范围,如表1所示。

表1　BOM活动节点的时间范围(λ=0.8，0.9)

4　结语

针对广义BOM建模中的4类BOM时间约束和模糊时间表达问题，建立了基于多色图的BOM时间数学模型，给出了一种BOM模糊时间的转换规则和基于最小时间距离的求解方法，建立了基于负环判定的BOM时间一致性判定方法。下一步的工作将研究BOM时间优化问题，分析各种BOM时差与BOM时间网络的内在联系，提出BOM时间调整的备选方案。

[1]李洲洋,田锡天,贾晓亮,等.基于SEBOM的飞机制造过程管理体系研究[J].西北工业大学学报,2008,26(6)：771-776．LiZhouyang,TianXitian，JiaXiaoliang，etal.SingleEnterpriseBOM-basedProcessManagementSystemforAircraftManufacturing[J].JournalofNorthwesternPolytechnicalUniversity，2008，26(6)：771-776.

[2]卢鹄，于勇，杨五兵，等．飞机单一产品数据源集成模型研究[J].航空学报,2010，31(4)：836-841.

LuHu，YuYong，YangWubing，etal.ResearchonIntegrationModelofSingleSourceAircraftProductData[J].ACTAAeronauticaEtAstronauticaSinica，2010，31(4)：836-841.

[3]赵岩，莫蓉，常智勇，等. 扩展型制造物料清单视图构建及其演绎机制[J]. 中国机械工程，2007,18(19):2334-2339.

ZhaoYan，MoRong，ChangZhiyong，etal.ConstitutionofanExtendedMBOMViewandItsDeductionMechanism[J].ChinaMechanicalEngineering，2007，18(19)：2334-2339.

[4]吕盛坪,乔立红,刘威.制造过程数据形式化语义建模[J].机械工程学报,2012,48(10):184-191.

LüShengping,QiaoLihong,LiuWei.FormalizedandSemanticModelingofManufacturingProcessData[J].JournalofMechanicalEngineering,2012,48(10):184-191.

[5]CaramiaM,GuerrieroF.ANoteontheModelingofProjectNetworkswithTimeConstraints[J].EuropeanJournalofOperationalResearch,2011,211(3):666-670.

[6]李若刚，王国祥，李跃，等．关于网络计划模型中的时间不确定性的讨论[J]. 系统工程与电子技术，1997，40(8)：40-45．

LiRuogang，WangGuoxiang，LiYue，etal.StudyonUncertaintyofActivityDurationofPERT[J].SystemEngineeringandElectronicTechnology，1997，40(8)： 40-45.

[7]徐瑞，徐晓飞，崔平远.基于时间约束网络的动态规划调度算法[J]. 计算机集成制造系统-CIMS，2004，10(2)：188-194．

XuRui，XuXiaofei，CuiPingyuan.DynamicPlanningandSchedulingAlgorithmBasedonTemporalConstraintNetwork[J].ComputerIntegratedManufacturingSystems，2004，10(2)：188-194.

[8]ZwickU.AllPairsShortestPathsinWeightedDirectedGraphs-exactandAlmostExactAlgorithms[C]//Proceedingsofthe39thIEEEAnnualSymposiumonFoundationsofComputerScience.LosAlamitos,CA:1998:310-319.

(编辑张洋)

Generalized BOM Time Modeling

Yan Chongjing

Nanjing University of Aeronautics and Astronautics,Nanjing,210016

A polygraph based method was proposed to describe time constraints and fuzzy time in one BOM.The time attributes was represented with fuzzy number and pigmentation of polychromatic set.Rules and approach were put forward to check and calculate the time consistency from BOM to time network.A case study was illustrated for evaluating the proposed method.

bill of material(BOM);time constraint network;fuzzy time;production schedule

2013-09-09

江苏省产学研联合创新基金资助项目(BY2014003-16);江苏省精密与微细制造技术重点实验室开放基金资助项目(JSPM201307)

TH166DOI：10.3969/j.issn.1004-132X.2015.02.009

闫崇京,男,1976年生。南京航空航天大学机电学院讲师。主要研究方向为数字化设计制造。发表论文10篇。