轮式自行火炮底盘匹配与优化
2015-10-29罗中峰徐亚栋
罗中峰 徐 诚 徐亚栋
南京理工大学,南京,210094
轮式自行火炮底盘匹配与优化
罗中峰徐诚徐亚栋
南京理工大学,南京,210094
为解决轮式自行火炮底盘匹配问题,以某8×8轮式自行火炮为例提供了一套匹配优化方案。该方案采用多学科设计优化的思想,首先依据匹配要求将轮式自行火炮底盘匹配模型分解,规定各个子模型相应的功能,并建立优化模型;然后将单学科可行法优化策略引入辅助设计变量,选用由第二代非劣排序遗传算法和序列二次规划法构成的组合算法进行求解;最后通过计算实例验证了方案的合理性。
轮式自行火炮;底盘;多学科优化设计;机动性;发射动力学;平顺性
0 引言
现代战争特别是高科技条件下的局部战争对轮式自行火炮的战术性能提出了越来越高的要求,这使得轮式自行火炮底盘的匹配与优化问题越来越突出。由于目前有关自行火炮的研究主要偏重于自行火炮某一性能[1-3]和火炮自身结构[4],因此轮式自行火炮底盘匹配与优化问题长期得不到解决。笔者基于多学科设计优化分析复杂系统的思想[5],以某8×8轮式自行火炮为例进行了轮式自行火炮底盘匹配与优化的研究工作。
1 学科分解与系统分析
1.1学科分解
本文以自行火炮作战效能指标[6](图1)为基础进行轮式自行火炮底盘匹配与优化的学科分解。与底盘相关的指标如下:机动性能指标、毁伤能力指标中的发射精度和携弹量、防护能力指标、设备维护指标中的运输适应能力。携弹量和防护能力用底盘载重量来衡量,载重量越大,携带弹药和防护装备的数目就越多,但同时也会降低自行火炮的机动性能;发射精度可以通过基于底盘的发射动力学模型来考查;运输适应能力通过基于底盘的行驶平顺性模型来考查。根据上述各个性能指标之间的关系和考查方式的不同,可以将轮式自行火炮底盘匹配与优化模型细分为以下3个基于底盘的子模型:机动性模型(考查机动性、载重量)、发射动力学模型、行驶平顺性模型。

图1 自行火炮作战性能评估指标
1.2系统分析

图2 自行火炮子系统耦合关系图
自行火炮各子系统的耦合关系可用图2表示。
1.2.1机动性模型
最大行驶速度(km/h):
(1)
式中,ηt为行驶系统的总效率;PeN为动力装置的最大输出功率,kW;fv为地面变形阻力系数;δb为质量增加系数;m为自行火炮的战斗全质量,t;g为重力加速度,m/s2。
单位质量功率(kW/t):
Pm=ηtPeN/m
(2)
作战行程(km):
(3)
式中,Q为油箱容积,L;Hu为燃油低燃值;ρ为燃油密度,kg/m3;ηs为动力装置的热效率。
纵向坡度角[7]:
(4)
式中,Me为动力装置的最大输出扭矩,N·m;ic为自行火炮行驶系统的最大传动比;r为车轮半径,m。
最小制动距离[8]:
(5)
式中,φ为地面附着系数;CS为空气阻力系数;AV为自行火炮在行驶方向的正投影面积,m2;ρs为环境大气密度,kg/m3;vr为行驶过程中自行火炮相对空气的速度,m/s。
自行火炮载重量即战斗全质量减去火炮、悬挂和车轮的质量(t):
m1=m-m2-m4
(6)
式中,m2为火炮质量(包括炮身、摇架、炮塔等),t;m4为悬挂和车轮质量,t。
1.2.2发射动力学模型
(1)后坐阻力。反后坐装置的引入,使得发射过程中火炮传递给自行火炮车体的力不再是炮膛合力,而是反后坐装置传递的后坐阻力FR[9]:
(7)
式中,FR0为初始后坐阻力;FRg为后效时期后的坐阻力;tg为弹丸在膛内运动时间;tr为从弹丸启动到后效期结束的时间。
(2)发射动力学模型。自行火炮发射时,车体的振动是一个相当复杂的多自由度振动。为了便于优化,本文将整个车体看成一个整体,并只考虑车体的上下振动、前后振动与俯仰振动。已知底盘的载重量为m1,绕车体质心的转动惯量为I1,火炮质量为m2,绕车体质心的转动惯量为I2,其他变量如图3所示。
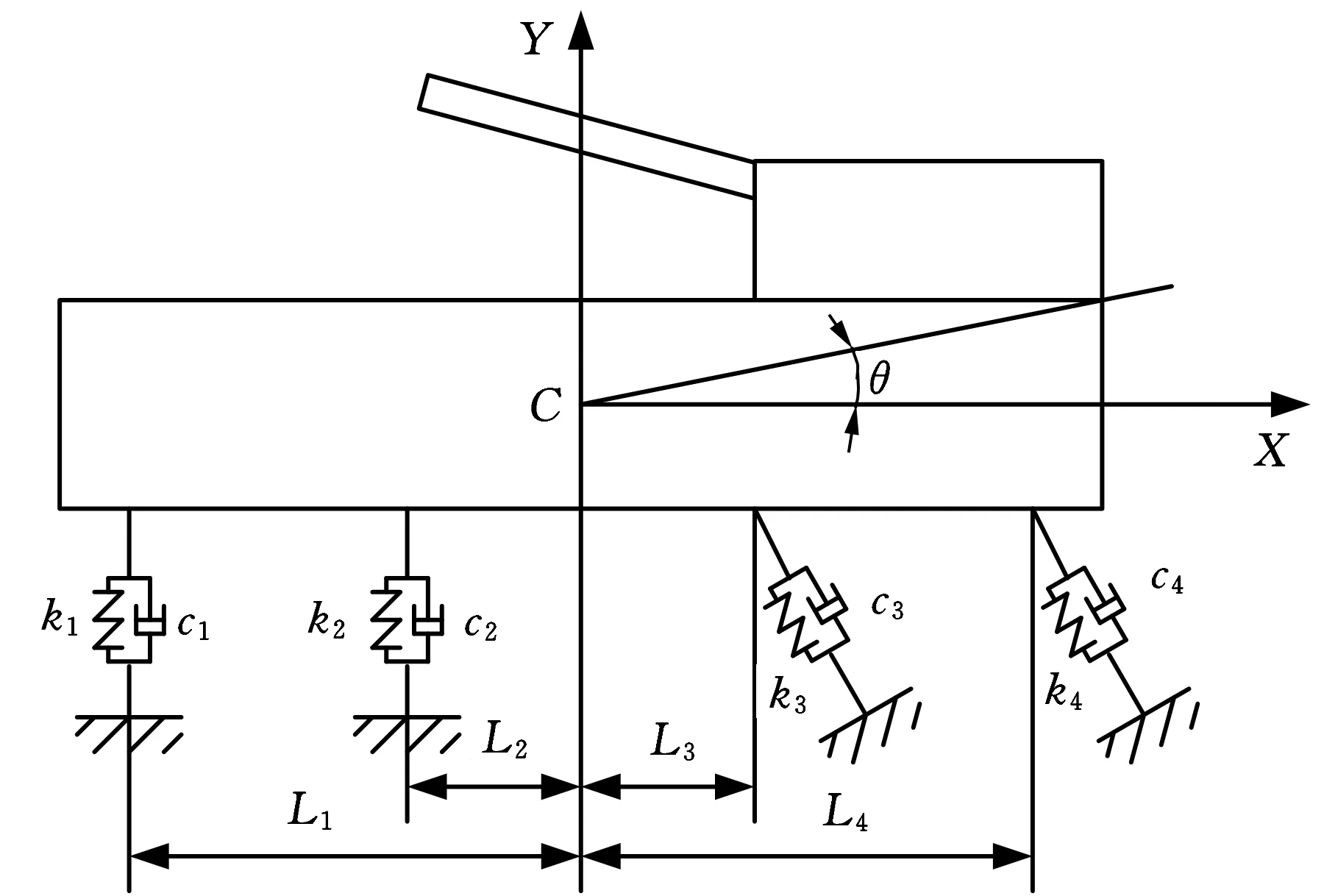
图3 某自行火炮发射动力学模型
取车体初始质心位置C为坐标原点,以水平向左为X轴正向,铅垂向上为Y轴正向建立图3所示的坐标系,车体绕质心的转角为θ,逆时针方向为正。由拉格朗日方程,得到系统运动微分方程:
(8)
式中,FRy为后坐阻力在垂直方向的分力;FRx为后坐阻力在水平方向的分力;MR为后坐阻力作用于车体质心的力矩;Li为第i排悬架与自行火炮的车体质心的水平距离;x为车体质心的水平坐标;xi为第i排悬挂的水平坐标,i=1,2,3,4。
为了完整评价车体跳动,以F的值作为车体跳动的评判(F的值越大跳动越大):
F=w1(maxy-miny)/y*+w2(maxx-
minx)/x*+w3(maxθ-minθ)/θ*
(9)
式中,w1、w2、w3为权重系数;y*、x*、θ*为归一化系数。
(3)后坐静止性。自行火炮的后坐静止性要求射击时自行火炮车轮始终与地面接触并沿水平方向不移动。若要达到上述要求,则必须满足下式:
FRcosβ≤μ1mg
(10)
式中,β为自行火炮射击高度角;μ1为路面的静摩擦因数。
β=0时,水平后坐阻力最大,有FRcosβ=FR,保证此时自行火炮静止应有
J1=FR-μ1mg≤0
(11)
(4)后坐稳定性。自行火炮的后坐稳定性要求火炮射击时车轮始终与地面接触。若要达到上述要求,则必须满足下式:
W=MR-mgL4≥0
(12)
1.2.3行驶平顺性模型
(1)路面激励。本文采用滤波白噪声作为路面输入模型[10],即

(13)
式中,q(t)为路面不平度位移输入;Gq(n0)为路面不平度8级分类标准中规定的路面不平度系数几何平均值;w0(t)为协方差为1 m2/s的单位白噪声。
本文采用E级路面谱,测试距离为1000 m。
(2)平顺性模型。轮式自行火炮行驶模型如图4所示,其中,qi(t)为路面不平度位移输入,a1、a2、a3为轮距,C为车体质心。

图4 某自行火炮行走动力学模型
由拉格朗日方程,得到系统运动微分方程:
(14)
(3)车辆平顺性评价。车辆的平顺性是评价车辆性能的重要指标,ISO2631/1给出了平顺性评价的近似方法:用车体质心垂直方向的加速度aw来评价车辆的平顺性[11]。规定:aw≤0.315m/s2为舒适;0.315
2 优化模型
2.1优化准则与目标函数
本文研究的目的是在火炮(包括炮身、摇架、炮塔等)的各种特性不变的情况下,选择合适的底盘参数,使自行火炮的相关性能达到最优。通过分析自行火炮的作战效能指标和系统分解结果可以发现,在同样的条件下,底盘载重量m1是影响自行火炮机动性的最大因素,m1越小,机动性越强,作战行程愈大,防护性能的加强、载弹量的提高都要求加大m1,并且m1也是影响自行火炮车体扰动、静止性、稳定性和行驶平顺性的重要因素,所以选择一个合适的m1相当重要。需要补充说明的是,研究过程中底盘的外形以及各悬挂的位置和轮胎都是不变的。综合上面几点,在保证机动性等要求的情况下,以底盘的载重量m1最大为目标函数。除此之外,还要考虑底盘参数对自行火炮发射速度和射击精度的影响,因为这两个指标是自行火炮射击指标中与底盘参数直接相关的,通过控制底盘参数,可以控制发射时车体的扰动,降低其对发射速度和射击精度的影响。针对这点,要求最大高低角发射时车体在垂直面内的扰动最小。由上述分析得到如下目标函数:轮式自行火炮底盘载重量最大即max(m1);高低角最大时发射后车体在垂直面内的扰动最小即min(F)。
2.2设计变量
本模型有如下的设计变量:动力装置的最大输出功率PeN、动力装置的最大输出扭矩Me、自行火炮的战斗全质量m、自行火炮行驶系统的最大传动比ic、自行火炮的油箱容积Q、第1排悬挂的阻尼c1和刚度k1、第2排悬挂的阻尼c2和刚度k2、第3排悬挂的阻尼c3和刚度k3、第4排悬挂的阻尼c4和刚度k4、自行火炮的车体质心的水平坐标x、自行火炮载重量绕车体质心的转动惯量I1。
2.3设计约束
本模型有如下的设计约束:自行火炮最大行驶速度v≥vmin,最小单位质量功率Pm≥Pmin,作战行程s≥smin,纵向坡度角α1≥αmin,最小制动距离S1≤Smin,后坐时自行火炮的静止性指标J1≤0,后坐时自行火炮的稳定性指标W≤0,行驶时自行火炮车体质心在垂直方向的加速度aw≤amin。
3 优化策略及优化算法
3.1优化策略
优化策略是在寻优算法的基础上提出的设计计算框架。选择合适的策略能够更好更快地找到最优解。由上节的系统分析可知:各子系统间有较多的公共设计变量和耦合设计变量,即各子系统间存在较强的耦合。多级优化策略和多学科可行法在处理强耦合系统时效率较低。同等情况下,多学科可行法比单学科可行法的计算复杂度高。考虑到上述几点,本文采用单学科可行法优化策略。单学科可行法是一种单级多学科优化策略,它通过引入辅助设计变量,实现子模型之间的解耦。针对本文所述耦合模型,单学科可行法的具体处理过程如下:
对于耦合设计变量m,引入辅助设计变量m′,附加约束为
h1=m-m′=0
(15)

(16)
对于耦合设计变量v,引入辅助设计变量v′,附加约束为
h3=0.6v-v′=0
(17)
其中,v为自行火炮最大行驶速度,正常行驶速度取最大行驶速度的60%。
引入辅助设计变量之后,各个子系统就可以单独建模。建模过程中,可以根据已引入辅助设计变量的情况,对子系统的输入做适当的调整。
3.2优化算法
优化算法应根据实际优化问题的特点进行选择。由于本文的优化模型是一个多峰模型,为了获得全局最优解,本文选用了由第二代非劣排序遗传算法和序列二次规划法构成的组合算法。在优化过程中,首先应用第二代非劣排序遗传算法在设计空间进行多目标全局搜索,求出Pareto解集,然后对Pareto解集中的各解进行如下计算:
f=1-F+(m1-m10)/m10=m1/m10-F
(18)
式中,m10为底盘载重量的初始值。
找出f值最大的X1(扰动下降的百分比和载重量上升的百分比之和最大的点)。接着应用序列二次规划法以X1为起点进行局部精确寻优。在精确寻优过程中以f值最大为目标函数,设计变量的范围以及约束同全局搜索时一样。具体的寻优过程如图5所示。

图5 优化设计流程
4 计算实例

综合图6、图7可以看出,优化结果是收敛的。由表1可以看出,载重量增加了21.0%,扰动下降了18.5%,各项约束都满足要求;同时附加约束的残差也较小(h1=0.34,h2=0.53,h3=0.14)。综合上述结果可知,优化是成功的,优化模型是合理的。虽然单位质量功率Pm、最大行驶速度v、作战行程s比优化前减小,但还满足设计约束,同时通过优化也使先前不满足约束的指标纵向坡度角α1和车体质心垂直方向的加速度aw满足了约束,满足约束的指标后坐时自行火炮的静止性指标J1和后坐时自行火炮的稳定性指标W得到加强。总之,优化提高了自行火炮的性能,使自行火炮总体资源得到了更加合理的利用。

图6 载重量收敛历程

图7 车体跳动收敛历程

参数优化前优化后约束优化后比较Pm(kW/t)34.9932.1≥30满足s(km)941.6866.8≥800满足α1(°)26.433.6≥30满足S1(m)3.83.36≤5.0满足v(km/h)112.0103≥100满足aw(m/s2)0.650.53≤0.63满足J1(N)-9984-20000≤0满足W(N·m)-13986-28450≤0满足m1(t)12.815.5增加21.0%F1.00.815下降18.5%
5 结语
本文针对轮式自行火炮底盘匹配与优化问题,提出了一种学科分解方案;以底盘载重量最大和最大射角时车体扰动最小为优化目标,建立了一套轮式自行火炮底盘匹配优化方案;应用单学科可行法优化策略处理了该模型的耦合关系;选用由第二代非劣排序遗传算法和序列二次规划法序列二次规划法构成的组合算法进行求解;最后通过具体实例验证了匹配优化方案的合理性。
[1]向涛波,刘重发,赵凌,等.某型自行火炮行驶平顺性仿真研究[J].机械设计与制造,2011(10):220-222.
Xiang Taobo,Liu Chongfa,Zhao Ling,et al.Modeling and Simulation on Ride Comfort of a Self-propelled Gun[J].Machinery Design & Manufacture,2011(10):220-222.
[2]吴大林,马吉胜,杜中华,等.自行火炮扭力轴强化疲劳寿命计算及分析[J].计算机仿真,2012,29(10):30-33.
Wu Dalin,Ma Jisheng,Du Zhonghua,et al.Calculation and Analysis on Fatigue Life of Torsion Link for Self-propelled Gun on Enhancement Road[J].Computer Simulink,2012,29(10):30-33.
[3]李本朋,潘玉田,李永强.某自行火炮的弹药架路面谱响应分析[J].机械管理开发,2011(1):28-31.
Li Benpeng,Pan Yutian,Li Yongqiang.The Response Analysis of the Road about a Ammunition of the Self-propelled Artillery[J].Mechanical Management and Development,2011(1):28-31.
[4]宋焦,何永,赵威,等.某迫榴式火炮反后坐装置的结构优化及分析[J].四川兵工报,2013,24(7):22-24.
Song Jiao,He Yong,Zhao Wei,et al. Optimal Structural Design and Analysis on Recoil Mechanism of Howitzer Mortar[J]. Journal of Gun Launch & Control,2013,24 (7):22-24.
[5]梅小宁,杨树兴.复杂系统的多学科设计优化综述[J].工程设计学报,2010,17(3):173-180.
Mei Xiaoning,Yang Shuxing. Review of Multidisciplinary Design Optimization for Complex Systems[J]. Journal of Engineering Design,2010,17(3):173-180.
[6]杨志强,易华辉,唐志跃.基于三角白化权函数的自行火炮作战效能评估[J].四川兵工报,2011,32(10):58-60.
Yang Zhiqiang,Yi Huahui,Tang Zhiyue. Operational Effect Evaluation of Self-propelled Guns Based on Triangle Whitening Function[J]. Journal of Gun Launch & Control,2011,32(10):58-60.
[7]毕小平,王谱凯.坦克动力-传动装置性能匹配与优化[M].北京:国防工业出版社,2004.
[8]王良曦,王红岩.车辆动力学[M].北京:国防工业出版社,2008.
[9]高跃飞.火炮反后坐装置设计[M].北京:国防工业出版社,2010.
[10]吴志成,陈思忠,杨林,等.基于有理函数的路面不平度时域模型研究[J].北京理工大学报,2009,29(9):795-798.
Wu Zhicheng,Chen Sizhong,Yang Lin,et al.Model of Road Roughness in Time Domain Based on Rational Function[J].Transactions of Beijing Institute of Technology,2009,29(9):795-798.
[11]蔡树新.自行火炮行驶试验路面谱仿真研究[D].石家庄:军械工程学院,2003.
(编辑张洋)
Matching and Optimization for Chassis System of Wheeled Self-propelled Guns
Luo ZhongfengXu ChengXu Yadong
Nanjing University of Science and Technology,Nanjing,210094
In order to deal with the optimum design for the chassis system(CS) of wheeled self-propelled guns,the way of MDO was introduced for analyzing the complicated system.Taking optimum design for a 8 by 8 wheeled self-propelled gun for instance,the optimization model was established,then was partitioned into several subsystems.In accordance with the requests for the chassis matching with the fire system the respective computation models were provided.Subsequently the coupling relationships among subsystems were analyzed in a manner of MDO.Finally,the instrumental variables were introduced to decouple subsystems from each other by the individual disciplinary feasible strategy.A combinatorial optimization algorithm of non-dominated sorting genetic algorithm Ⅱ and sequential quadratic programming was selected to optimize the resulting problem and the calculation example was verified the validity of this design pattern.
wheeled self-propelled gun;chassis;multidisciplinary design optimization(MDO);mobility;launch dynamics;riding comfort
2013-09-10
国防基础科研项目(A262011003)
TJ303DOI:10.3969/j.issn.1004-132X.2015.02.004
罗中峰,男,1984年生。南京理工大学机械工程学院博士研究生。主要研究方向为多学科优化。徐诚,男,1962年生。南京理工大学机械工程学院教授、博士研究生导师。徐亚栋,男,1978年生。南京理工大学机械工程学院副教授。
