变刚度电液力加载系统性能研究

傅晓云　贺向宗　李宝仁

华中科技大学,武汉,430074

变刚度电液力加载系统性能研究

傅晓云贺向宗李宝仁

华中科技大学,武汉,430074

针对海洋船舶拖曳系统半实物仿真的需要，设计了以钢丝绳为力传递介质的电液力加载系统。建立了力加载系统的数学模型，通过试验得出了钢丝绳刚度与加载力的对应关系式；分析了钢丝绳刚度对系统性能、控制器设计的影响，得出钢丝绳刚度减小会导致力加载系统频宽减小、滞后增大的结论。基于此设计了变增益前馈补偿控制器。试验结果表明，该方法提高了系统加载力跟踪精度。

电液力加载；钢丝绳刚度；复合控制；输入前馈

0　引言

海洋船舶拖曳系统是一种广泛应用于海洋作业的水下装置,应用前需要进行大量试验验证,而传统的海上试验成本高、周期长，不能满足频繁试验的要求。为此,采用负载模拟器对装置进行半实物仿真试验，以提高试验效率,降低试验成本,改良试验条件。

1　电液力加载装置模型的建立

电液力加载装置结构如图1所示,其中,力加载系统采用阀控液压马达形式，以钢丝绳为力传递介质，用来复现海洋船拖曳过程中的拉力变化(模拟吊放重物从水上状态到水下状态的力变化过程)。加载力在8～120 kN范围内连续变化,力加载装置频率为0.05～1 Hz。

1.速度编码器　2.伺服阀　3. 液压马达　4.力加载绞车　5.拖曳绞车　6.拉力传感器　7.钢丝绳　8.伺服阀　9.液压马达　10.惯性装置　11.钢丝绳等效弹簧刚度图1　海洋船拖曳系统试验室半实物仿真结构原理图

对电液力加载装置进行数学建模时,假定拖曳装置转速为0,伺服阀简化为比例环节。由图1及阀控马达的基本方程[1]得出系统方框图(图2)。由图2得系统开环传递函数(忽略外扭矩干扰TL)：

(1)

式中,Kv为系统的开环增益,Kv=KeKaKsvkR/Dm;Ke为力误差信号转换为直流电压信号增益;Ka为伺服放大器增益;Ksv为伺服阀流量增益;k为钢丝绳刚度;R为卷筒半径;Dm为液压马达排量;Vt为液压马达两腔及连接管道总容积;Kce为总流量-压力系数;Jt为液压马达和负载折算到马达轴上的总惯量;Bm为液压马达和负载的黏性阻尼系数;K为有效体积弹性模量。

将式(1)简化为[1-2]

(2)

式中,ωr为惯性环节转折频率;Gh为液压扭转弹簧刚度;Kx为系统的开环增益;ω0为综合固有频率;ξ0为综合阻尼比。

由式(2)可以看出,钢丝绳刚度k是关系到系统性能的重要参数,影响系统的转折频率、综合固有频率、综合阻尼比。因此，文中以钢丝绳刚度k为主线，对力加载系统性能、控制策略进行讨论。

2　钢丝绳刚度确定

实际使用中,钢丝绳直径为32 mm,两装置的水平间距为20 m,钢丝绳简化模型如图3所示,一端固连,一端加载。假设钢丝绳初始所受拉力为F,由于钢丝绳受重力和集中载荷的作用,其实际轨迹线为L。当拉力增加ΔF时,钢丝绳长度将减小Δl(分别为弹性变形和克服重力的位移变形),钢丝绳轨迹线变为图3中的虚线。因此钢丝绳刚度应包括弹性刚度和克服重力刚度。

图2　电液力加载装置的系统方框图

图3　钢丝绳简化模型

钢丝绳的弹性模量或刚度与布置结构、所受拉力、自身长度、使用时间等众多因素有关[2]。为得到系统中钢丝绳刚度的准确值，对系统进行定量分析，研究中采用位移-拉力试验法来求解钢丝绳刚度。试验中，利用电液力加载装置输入阶跃信号(阶跃信号从10 kN开始,每次跳跃幅值为10 kN，直至到达120 kN),用速度编码器对时间积分得出位移变化Δl。多次测量后,利用虎克定律得出当前拉力下的钢丝绳刚度。图4、图5所示分别为拉力阶跃响应和对应速度曲线。

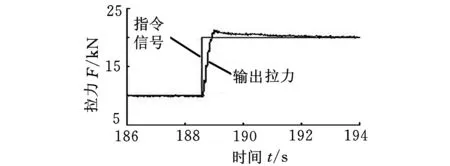
图4　阶跃响应曲线

图5　阶跃响应时速度曲线

试验得出的钢丝绳刚度曲线如图6所示,运用最小二乘法二次拟合得到的曲线表达式为

k=-6.667×10-5F2+25.5F+2.03×105

(3)

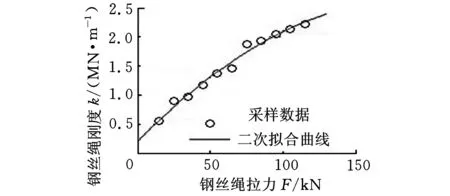
图6　钢丝绳刚度同所受拉力对应关系

从图6和式(3)可知,钢丝绳刚度随所受拉力的增加而增加，呈非线性。

3　钢丝绳刚度变化对系统性能的影响

已知系统中各项参数:Dm=1.201×10-3m3/rad,Ke=0.6×10-5V/N,Vt=9.04×10-3m3,Ka=1.0×10-3A/V,Jt=720 kg·m2,Ksv=0.33 m3/(A·s),Bm=0.1 N·m·s/rad，Kce=1.1×10-11m5/(N·s),K=700 MPa,R=0.34 m。

为分析钢丝绳刚度变化对系统性能的影响,选取拉力为10 kN、30 kN、60 kN、90 kN(对应图7中曲线1～4)时对应钢丝绳的刚度为研究对象，将参数分别代入开环传递函数(式(2))中，得出4个点分别对应的Bode图(图7)。

(a)幅频曲线

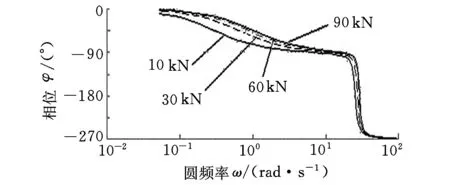
(b)相频曲线图7　系统开环频率特性曲线

从图7看出:当钢丝绳刚度k减小时,系统转折频率ωr、穿越频率ωc降低,频宽减小,且小于1 Hz;幅值裕度和相位裕度增加,系统的稳定性变好,但系统在1 Hz附近响应变慢,力跟踪滞后严重。

加载力在连续变化时,为了消除钢丝绳刚度变化对系统性能的影响,采取的主要方法有:①在结构上,若条件允许,安装排揽机构,增加钢丝绳的支撑点，使钢丝绳尽量水平，以减小钢丝绳刚度的变化范围，限制钢丝绳抖动；②在控制上，采用插值法实时调整PID控制器参数或者采用自适应控制器等[2,4];③对于力跟踪相位滞后严重的现象，仅应用反馈控制器是不够的,需在控制器中增加输入前馈补偿来提高力跟踪精度[5-8]。

4　变钢丝绳刚度对前馈补偿系数的影响

为了提高系统的力跟踪精度,消除相位滞后,控制器中引入了输入前馈补偿环节,优点在于[5-8]:①从理论上分析,当补偿器满足一定条件时,系统输出量可完全复现输入量,且误差恒为0;②前馈补偿为开环控制方式,不会影响到系统的稳定性,不改变反馈控制系统的特性;③前馈控制减轻了反馈控制的负担,反馈控制的增益可取得小一些,有利于系统的稳定。复合控制器原理如图8所示,其中,Gr(s)为输入前馈补偿传递函数,如式(4)所示;G0(s)为反馈控制器,文中为PID控制器;G(s)为系统的开环传递函数,如式(2)所示，其中H(s)为1。

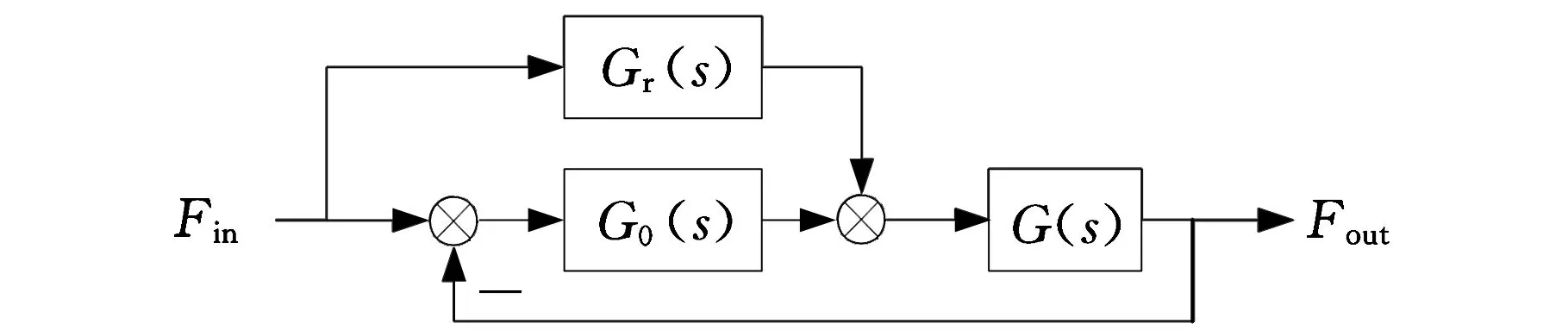
图8　含输入前馈补偿的复合控制系统方框图

对输入的全补偿条件为[6]

Gr(s)=1/G(s)

(4)

由于G(s)很难准确知道,所以输入全补偿在物理上往往无法准确实现。然而通过图7系统开环Bode图得出,影响系统性能的主要因素为惯性环节，因此可将G(s)简化为惯性环节,则Gr(s)=(s+ωr)/(ωrKx)。该方法不仅减小了相位滞后,而且容易实现。

根据式(2)和第3节的分析得出:系统转折频率ωr同钢丝绳刚度k有关,且随钢丝绳刚度k增大而增加；因此在进行输入前馈补偿时，一次项系数应随输出力的变化而实时不断调整，且其值随输出力的增大而减小。

在系统试验中,分别采用无输入前馈的PID控制器和加输入前馈的PID控制器,对幅值为5 kN,频率为1 Hz,偏置分别为30 kN和60 kN的力正弦信号进行跟踪,试验结果如图9～12所示。

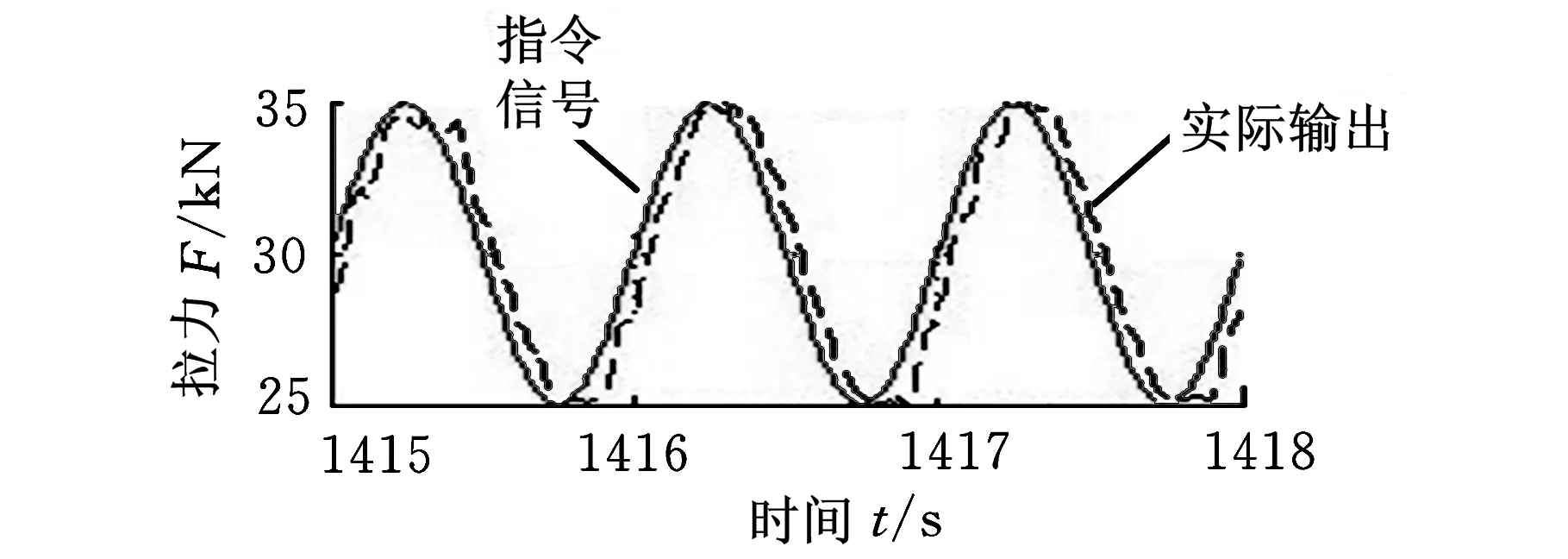
图9　30 kN处1 Hz控制曲线(无前馈)

图10　60 kN处1 Hz控制曲线(无前馈)

图11　30 kN处1 Hz控制曲线(有前馈)

图12　60 kN处1 Hz控制曲线(有前馈)

试验证明:前馈补偿后,跟踪相位分别由18.57°、18.64°减小为5.74°和4.46°,在控制器中加入输入补偿提高了系统力跟踪精度,减小了相位差;钢丝绳刚度随输出力变化,使得ωr为变量,因此输入一次项系数应随输出力变化进行实时调整,如在含前馈补偿试验时,前馈的一次项系数在偏置为30 kN时为0.4,60 kN时为0.35。

5　结论

(1)通过位移-拉力试验法和最小二乘曲线拟合法,得出了钢丝绳刚度与加载力的关系式，为系统性能分析、高性能控制器的设计提供了依据。

(2)由系统Bode图可以看出，钢丝绳刚度随加载力的变化而变化，影响到力加载系统的频宽、响应速度、稳定裕度。

(3)试验表明，在控制器中加入输入补偿，并对补偿器一次项系数进行实时调整后，相位滞后减小到10°以内，提高了力跟踪精度。

[1]王春行.液压控制系统[M].北京:机械工业出版社,1999.

[2]张利顺,张玉珊,王秀波,等.钢丝绳弹性模量研究的现状与发展方向[J].林业科技,1996(6):55-57.

Zhang Sunli,Zhang Yushan,Wang Xiubo,et al.Present Status and Development Direction of the Steel Wire Rope of the Elastic Modulus[J].Forestry Science & Technology,1996(6):55-57.

[3]赵克定，刘冬. 负载刚度对主动式电液力控制系统性能的影响[J].液压·气动·密封,2005(6):23-24.

Zhao Keding,Liu Dong.Effection of Load Rigidity to the Performance of Active Electro-hydraulic Force Controlling System[J].Hydraulics Pneumatics & Seals,2005(6)：23-24.

[4]奥斯特隆姆 K J,威顿马克 B.自适应控制[M].李清泉,李翔,张兆义,等,译.北京:科学出版社,1992.

[5]Alleyne A, Liu R. On the Limitation of Force Tracking Control for Hydraulic Servos Systems[J]. Journal of Dynamic Systems,Measurement and Control,1999,121(2):184-190.

[6]冯巧玲.自动控制原理[M].2版.北京:北京航空航天大学出版社,2007.

[7]焦宗夏,华清,王晓东,等.电液负载模拟器的复合控制[J].机械工程学报,2002,12(12):34-37.

Jiao Zongxia,Hua Qing,Wang Xiaodong,et al.Hybrid Control on the Electro-hydraulic Load Simulator[J].Chinese Journal of Mechanical Engineering,2002,12(12):34-37.

[8]Tomizuka Masayoshi. Adaptive Zero Phase Error Tracking Algorithm for Digital Control[J].Journal of Dynamic Systems,Measurement and Control,1987,109:349-354.

(编辑张洋)

Investigation of Electro-Hydraulic Loading System with Variable Stiffness

Fu XiaoyunHe XiangzongLi Baoren

Huazhong University of Science and Technology,Wuhan,430074

An electro-hydraulic loading system,conveying force by wire-rope,was designed to meet the requirements of hardware-in-the-loop simulations of the towing system in the marine vessel.A mathematical model of the electro-hydraulic loading system was presented herein.The relationship expression between the wire-rope stiffness and the loading force was derived from the results of experiments.Through the analysis of the effect of the wire-rope stiffness on the performance of the loading system and the design of the controller,it is concluded that the frequency width minifies and hysteresis increases with the wire-rope stiffness decreases.Then a variable gain feed-forward compensation controller was designed.Experimental results show that this method can improve force tracking accuracy of the system.The paper provides a theoretical basis for high performance electric hydraulic loading system controller design with variable stiffnesses.

electro-hydraulic loading system;wire-rope stiffness;composite controller;input feed-forward

2013-09-03

TH137DOI：10.3969/j.issn.1004-132X.2015.02.011

傅晓云,男,1970年生。华中科技大学机械科学与工程学院副教授。主要研究方向为气动、液压控制技术。获教育部科技进步一等奖1项。发表论文20余篇。贺向宗,男,1988年生。华中科技大学机械科学与工程学院硕士研究生。李宝仁,男，1962年生。华中科技大学机械科学与工程学院教授、博士研究生导师。