切削比能模型的建立及参数影响分析
2015-10-28张洪潮孔露露陈俊超
张洪潮 孔露露 李 涛 陈俊超
大连理工大学,大连,116024
切削比能模型的建立及参数影响分析
张洪潮孔露露李涛陈俊超
大连理工大学,大连,116024
从材料去除机理角度分析了材料去除过程中的能量耗散机理,并对材料去除能耗进行建模量化,推导出切削比能经验公式。根据试验数据拟合出端面车削的切削比能幂率公式,拟合度在95%以上。鉴于切削参数对切削比能影响的差异性,结合试验分析了切削三要素对切削比能的影响机理,研究结果为面向节能的切削工艺参数的制定及低碳制造量化评估清单数据要求提供了基础支持。
材料去除;切削能量耗散;切削比能;车削;精益生产
0 引言
切削比能是指去除单位体积材料所需要的切削能量,它能够反映切削能耗与材料去除率之间的映射关系以及机床能效能力[1]。早在1992年,Warren[2]通过试验建立了切削比能的经验公式,以及100多种材料的切削比能基础数据。近年来,随着低碳制造及精益生产的兴起[3],为满足加工能耗计算和低碳制造量化评价的清单数据要求,切削比能更加受到国际学者的关注和应用。Draganescu等[4]通过研究指出铣床加工能耗、比能耗及能效是与切削参数和负荷密切相关的动态指标,提出了一种基于试验统计的机床能耗变化规律的建模方法。Gutowski等[5-6]在搜集了大量数据的基础上基于材料的平均切削比能建立了各种工艺的切削比能与材料去除率的映射图谱,半定量地反映了不同工艺的能效差异。Diaz等[7]通过试验分析了一个微加工中心在不同材料去除率下切削低碳钢的能量需求,建立了切削比能模型,指出材料的切削比能随着材料去除率的增大而降低,并将该规律拓展到大型机械加工设备中。Li等[8]通过试验建立了机床加工比能与材料去除率的函数模型,并将机床加工比能细化为五部分,但各部分的具体影响规律尚待进一步揭示。Pawade等[9]预测了高速切削铬镍铁合金718时主剪切区域内的切削比能解析模型,指出剪切比能是进给率的函数,随着进给率的减小而增大。Alessandro等[10]对高速切削条件下的切削比能与刀具几何参数及切削速度的关系进行试验研究。
综上可知,各国学者对切削比能的研究逐渐由试验统计建模上升到内在规律的理论揭示;由分析典型工艺条件下的限定性模型拓展到具有普适性、可比性的单元能耗模型的建立。然而,学术界还未对单个参数选取对切削比能的影响规律进行详细分析,且国内自主的切削比能数据、方法、手册尚待开发。本文从理论上揭示了材料去除能量耗散机理,并引入切削比能的概念对材料去除能耗进行量化建模,提出了一种根据已有的切削力数据计算切削比能的方法。通过试验建立了切削比能与切削参数之间的映射函数模型,并结合理论揭示了单个参数影响下的切削比能内在变化规律,为切削加工工艺方案的制定提供了基础指导。
1 切削比能模型的建立
1.1切削能量耗散机理
金属切削过程中的能量主要消耗在克服金属的弹塑性变形、前刀面与切屑的摩擦、后刀面与过渡表面及已加工表面的摩擦上[11],即三个变形区(Ⅰ、Ⅱ、Ⅲ)内。
如图1所示,第Ⅰ变形区为主要变形区,被切金属层在刀具前刀面的挤压作用下,随着刀具的逼近,被切金属沿滑移线产生剪切变形,表现为弹性变形、塑性变形、挤裂变形,最终被切离工件本体。刀具的机械能逐渐转换为材料的形变能,材料变形程度越高,材料强度硬度越大,耗能量越大。
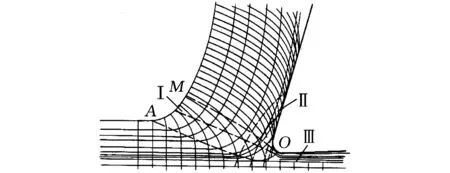
图1 金属切削过程中的滑移线和流线示意图[11]
被切金属经第Ⅰ变形区剪切滑移而形成的切屑,在沿前刀面流出时,进一步受到前刀面的挤压而产生剧烈摩擦,产生大量摩擦损耗。摩擦区域分为黏着区和滑动区。在黏着区,在切屑及刀具前刀面间大的压力及高温作用下,切屑底层与前刀面发生黏结,刀具和刀具黏结层与其上层金属间产生金属内部剪切滑移,内摩擦力大小与材料的流动应力特性及黏结面积有关。切屑离开黏结区后进入滑动摩擦区。在该区域内刀屑间的摩擦仅为外摩擦。而外摩擦的大小与摩擦因数以及压力有关,而与接触面积无关。该区域的摩擦作用产生大量的热量,造成热量的耗散。
由于刀具钝圆半径或负倒棱的存在使得切削层中有很薄一层无法切除而被刀具挤压留在已加工表面,该部分金属在沿后刀面流出时,又受到后刀面上一段棱面的挤压并相互摩擦,这种剧烈的摩擦使工件表层金属受到剪切应力,随后开始弹性恢复。该区域产生变形和回弹,造成表层金属的纤维化和加工硬化,形成加工变质层。机械能转化为新表面形成能。
由此可知,在切削过程中,机床系统向切削模块不断提供能量,切削模块的机械能逐渐转化为材料的形变能、摩擦热量及新表面形成能等,能量、物料、信息流在整个加工系统中的传递和转换使得加工任务得以实现。该过程中材料切削能可用以下公式进行计算:
Ec=Pcutt=(Fzv+Fxnwf)t=Ef+Qf+Enf
(1)
式中,Ec为工件切削能;Pcut为有效切削功率;Fz为主切削力;v为切削速度;Fx为进给力;nw为工件转速;f为进给量;t为加工时间;Ef为第Ⅰ变形区内材料变形能;Qf为第Ⅱ变形区内摩擦热量;Enf为第Ⅲ变形区新表面形成能。
1.2切削比能的引入
本文引入切削比能的概念解释材料去除能量的消耗机制,切削比能是指去除单位体积的材料所消耗的能量[11]。若已知一定工艺条件下加工特定材料的切削比能,则可得到整个工件加工中的材料去除能量为
Ec=esV
(2)
式中,es为材料的切削比能;V为材料的总去除体积。
金属切削过程是一个材料逐步去除的过程,切削比能是工件加工瞬时耗能量的量化,能够反映出切削能耗与切削参数之间的映射关系及机床能效能力,便于理解和计算,也是产品生命周期评估中的重要参数,被广泛应用于各种工艺中。切削比能一方面受加工环境的影响,另一方面与自身晶体结构有关。加工环境(包括加工参数、刀具参数及润滑条件等)主要通过影响材料的变形程度及工件与刀具间的摩擦力来影响切削比能的大小,切削参数的影响作用将在试验分析中进行详细解释。在微观角度,材料去除率相对大时,材料的去除主要在晶格缺陷处发生断裂,且材料去除率越大,由于晶格缺陷引起的断裂的可能性越大,能耗越低。在材料去除率非常小时,如微量磨削加工,必须依靠外力来破坏正常的晶格结构才能将晶粒剥离本体,耗能特别大,产热多,可以看到磨削时通常会有电火花出现。
1.3切削比能模型
综合目前对切削比能所作的研究[2-10,12-13],切削比能可归结为三个层次的建模:
(1)通过切削有效能建立起来的切削比能计算模型。该模型仅考虑去除材料部分的切削系统的有效输出耗能量,揭示材料净去除部分的耗能规律。计算模型如下:
(3)
式中,Pc为主轴切削功率;Z为材料去除率,cm3/min;η为主轴运行能量效率;es1为材料切削比能。
(2)建立在机床层,测量机床进行切削加工时的功率,进而建立机床进行材料去除时的比能耗模型:
(4)
Z′=1000apf v
(5)
式中,C0、C1为系数;Z′为材料去除率,同Z不一样的是Z′的单位为mm3/s;ap为背吃刀量。
该模型体现出不同机床的能耗差异,也反映出机床的能效能力,对于指导机床高效运作有重要意义。
(3)在批量生产中,将产品加工的整个过程的耗能量综合考虑所建模型,此模型是产品生命周期评估的重要参数,对于计算产品生产过程中的能耗量具有重要价值。该模型表达式为
(6)
式中,Etotal为加工一批零件的总耗能量;Vpart为加工一个零件所去除材料的体积;Npart为这批零件的数量。
但以上研究所建立的模型主要是以材料去除率为变量的函数,却忽略了材料去除率中单个参数对切削比能影响的差异性,只是定性地分析了材料特性、刀具形状及主轴驱动方式对切削比能的影响。若要定量地精确计算切削比能,需要研究分析单个参数对切削比能的影响。
后两个层次的模型主要决定于所选机床及工艺路径[14],虽然系统地反映出了工件加工过程中耗能量的多少,但其中真正用于材料去除的耗能量仅占30%左右[15],很难揭示材料去除本身的耗能特性。本文基于材料去除机理,对第一层次的切削比能进行细化建模。机床输出的有效能部分主要用于去除材料做功,有效切削功率直接体现在切削力与切削速度的物理关系上,在式(3)的基础上根据切削力与有效能耗的关系,可推导出切削比能的计算公式,即
(7)
式(7)中,Fxnwf是消耗在进给运动中的功率,它相对于Fz所消耗的功率来说,一般很小,可以略去不计[11](经计算,一般小于1%),于是
(8)
由式(8)可以看出切削比能与切削力是成正比的,而与进给速度、背吃刀量则呈幂次关系。由切削力的经验公式可知:
(9)
式中,K为决定于被加工金属和切削条件的系数;x、y、n分别为背吃刀量、进给量、切削速度对切削力的影响系数。
于是
(10)
式(10)给出了一种根据已有的切削力经验公式计算切削比能的方法。由此可见,材料的切削比能与切削参数也呈指数关系,因此可令切削比能经验公式为
(11)
式中,C为取决于材料和加工方式的系数;a、b、c为待定指数。
由于本文研究对象为切削比能,因此对切削比能进行重点拟合建模及规律分析。本文根据试验数据采用最小二乘法拟合出切削比能与切削参数的拟合回归方程,并检验了切削参数对回归方程的拟合显著性,最后采用单因素法对每个切削参数对切削比能的影响进行细化规律分析。
2 基于试验的切削比能变化规律分析
2.1试验条件
试验在一台CD6140A车床上进行,用YT15型硬质合金刀具对45钢棒料(长径比约为3)进行端面车削。试验中使用YDC-Ⅲ压电式切削力测试仪对切削力进行测量,利用YE5850电荷放大器对信号进行放大后,通过数据采集卡将数据采集到电脑,利用GDFMS软件进行数据的显示及处理(GDFMS软件具有时域处理功能,为降低试验中振动及噪声对数据准确度的影响,选用平滑滤波的方式,基于加权移动平均值的原理对干扰信号进行去除,经滤波处理后通过取平均值的算法得到所需切削力数值)。试验系统的组成如图2所示。

图2 外圆车削试验系统
装夹时采用顶尖进行支撑,试验所用刀具具有大前角小后角(主偏角60°,副偏角60°,刃倾角0°,前角15°,后角3°)。在进行试验测量前先对工件进行去皮试切,保证工件回转中心与主轴回转中心重合;待刀片稍微磨钝后(磨出圆弧过渡刃,其半径约为0.5 mm)再进行试验切削。首先采用33完全析因设计的试验方案,进行总体回归建模及检验。为直观揭示单个参数对切削比能的影响规律,绘制切削参数变动下的切削比能曲线,再进一步采用单因素法进行深入探究。
2.2切削比能模型的建立及验证
2.2.1多元线性回归分析[16]
对式(11)两边取对数得
lges=lgC+algap+blgf+clgv
(12)
令y=lges,x1=lgap,x2=lgf,x3=lgv,β0=lgC,则原指数方程可转换为线性方程:
y=β0+β1x1+β2x2+β3x3
(13)
其中,β1、β2、β3、β4为回归系数。根据27组试验测量值建立多元线性回归方程:
(14)
式中,εi为试验随机误差(i=1,2,…,27)。
式(14)用矩阵形式表示为
y=X β+ε
(15)
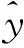
(16)
令
Q=(y-X β)T(y-X β)
(17)
则最小二乘估计量b应满足:
(y-Xb)′(y-Xb)=min((y-X β)T(y-X β))
(18)
将Q对b求导,并置为零,化简正规方程组得
b=(XTX)-1XTy
(19)
2.2.2试验数据处理与分析
将试验测得的27组试验数据代入回归方程,经上述最小二乘拟合得到端面车削45钢时切削比能的经验公式为
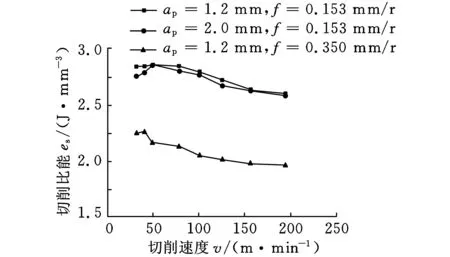
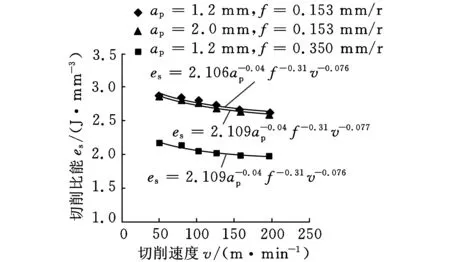
(20)
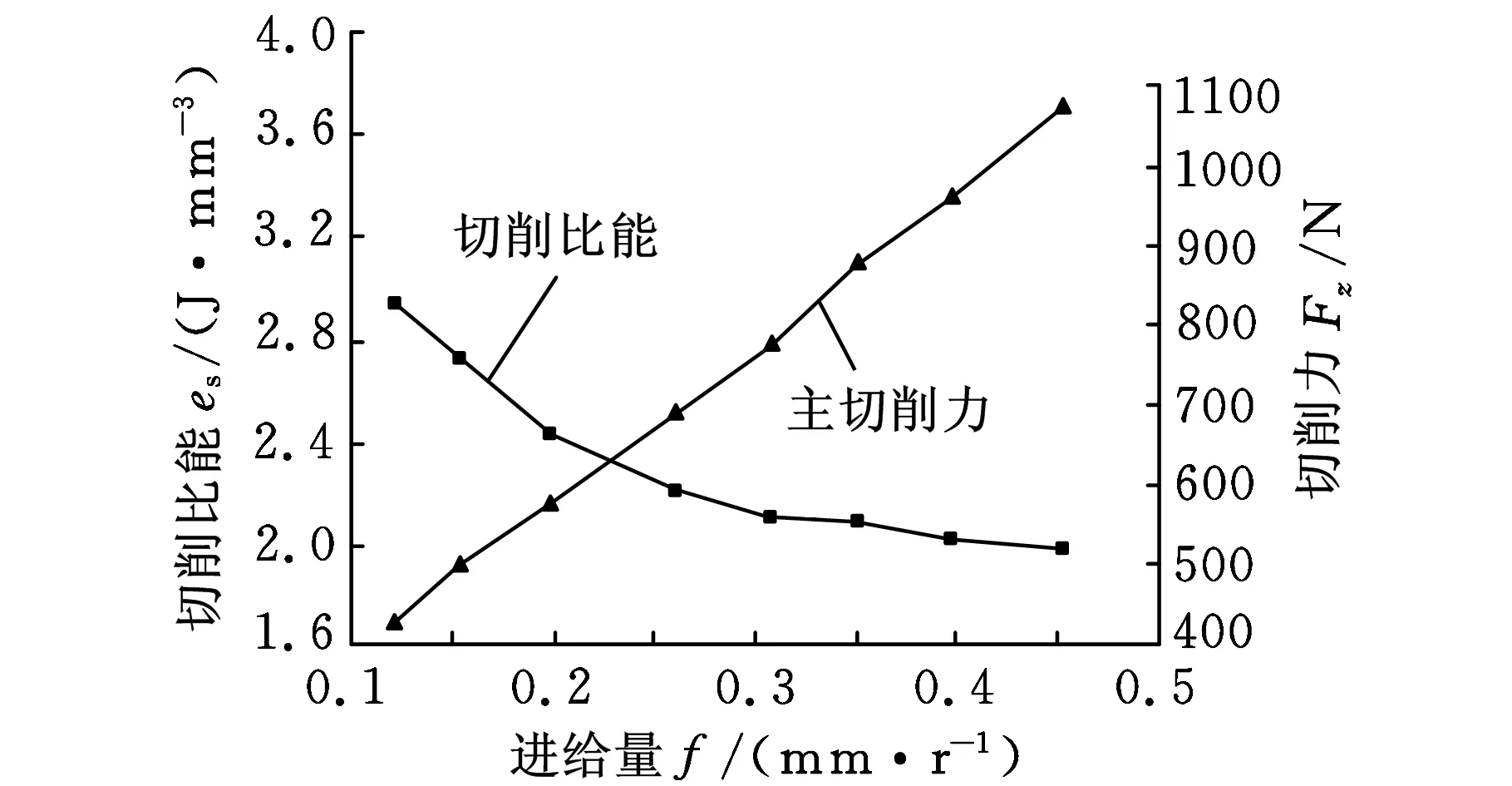
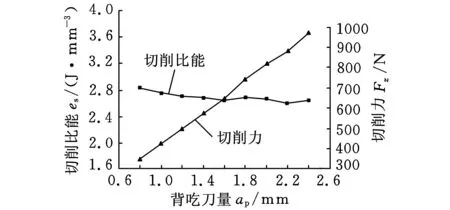
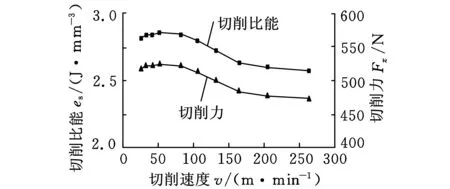
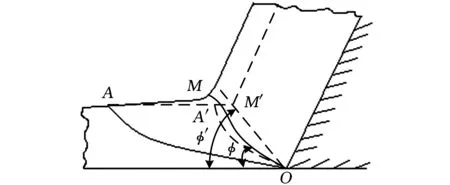
40 m/min 将式(20)计算得到的切削比能预测值与通过式(8)直接利用切削力计算得到的试验值进行比较,见表2。 利用数理统计知识,分别对该模型及回归系数的显著性进行检验。 (1)用F检验法对模型总体回归效果进行显著性检验。根据表2数据,经计算,可得残差平方和: (21) 回归平方和: (22) 选取检验统计量为 (23) 表2 切削比能及拟合值对比 (2)用t检验法对式(20)系数进行显著性检验,所用统计量为 (24) 其中,hii为(XTX)-1中相应的对角元素。查t分布表得t0.95(23)=2.0687,计算检验统计量的观察值如表3所示。 表3 回归系数显著性检验 表3的显著性分析显示,进给量、背吃刀量、切削速度与切削比能的指数拟合度在95%以上,而切削速度的拟合规律尚需进一步修正分析。 2.2.3切削比能模型的校正分析 采用单因素法进行多次试验,对切削速度对切削比能的影响进行规律探究,得到3组切削速度影响下的切削比能变化曲线,如图3所示。 图3 切削速度对切削比能的影响规律 由图3可见,当切削速度v<50 m/min时,随着切削速度的升高,切削比能首先逐渐增大,而当切削速度v>50 m/min时,随着切削速度继续升高,切削比能则逐渐降低(具体原因将在下节中详细展开)。 下面分段对其进行统计分析:当切削速度v<50 m/min时,切削较不稳定,由于工艺系统的振动对刀具产生冲击,以及积屑瘤的产生和消失等原因使切削力变化较大,根据所测数据进行拟合后分别得到es=2.02v0.08,es=2.64v0.02,es=2.72v0.01,它们差距较大,难以形成统计规律。而当切削速度v>50 m/min时,切削较平稳,图4所示为对所得数据进行拟合所得的曲线。 图4 切削比能与切削速度的拟合曲线 (25) 2.3切削参数对切削比能的影响分析 在切削系统已经确定的情况下,切削参数成为影响切削比能的主要因素,切削参数主要通过影响材料去除时的变形量及刀屑界面的摩擦力来影响切削比能。下面利用单因素法,结合切削力变化趋势,研究切削参数对切削比能的影响。 2.3.1进给量对切削比能及切削力的影响 图5 进给量对切削比能和切削力的影响曲线(ap=1.2 mm,v=80 m/min) 2.3.2背吃刀量对切削比能及切削力的影响 同进给量相似,背吃刀量增大切削面积增大,切削力及切削功率增大,由于背吃刀量基本对前刀面摩擦因数及材料变形系数没有影响,切削力的增大基本与背吃刀量的增大成正比,切削比能基本不变,如图6所示。由上述分析可知:从切削刀具上的载荷和能量消耗的观点来看,用大的进给量f工作比用大的背吃刀量ap对精益生产更为有利。 图6 背吃刀量对切削比能的影响曲线(f=0.153 mm/r,v=80 m/min) 2.3.3切削速度对切削力及切削比能的影响 图7所示为ap=1.2 mm、f=0.153 mm/r时切削速度对切削比能的影响曲线。在低速范围内(v<50 m/min时),随着切削速度的升高,摩擦因数增大。这是因为切削速度低时,切削温度较低,前刀面与切屑底层不易黏结,黏结情况随切削速度的升高而发展,使摩擦因数上升,材料与刀具间摩擦力的增大使得切削力和切削比能都增大。 图7 切削速度对切削比能的影响曲线(ap=1.2 mm,f=0.153 mm/r) 在切削速度继续升高时,温度进一步升高,材料塑性增加,流动应力减小,故摩擦因数下降,同时变性系数减小,原因有两点:第一,塑性变形的传播速度较弹性变形的传播速度慢。如图8所示,当切削速度低时,金属的始剪切面为OA,但当切削速度增高时,金属流动速度大于塑性变形速度,亦即在OA线上尚未显著变形就已流到OA′线上,使第一变形区后移,剪切角φ增大,也会导致变形系数减小。第二,切削温度升高,也使得被加工金属的强度硬度降低,于是去除材料所需能量减小,于是切削比能及切削力都将减小。 图8 切削速度对剪切角的影响 本文从切削机理角度,分析了材料去除过程中能量耗散机理,引入切削比能的概念,提出根据已有切削力数据建立切削比能经验公式的方法。并基于特定试验环境拟合出外圆车削45钢时的切削比能经验公式(试验条件不同,公式中拟合系数会稍有不同,但切削参数对切削比能的影响趋势不会改变)。另外,从切削变形机理角度对切削三要素对切削比能的影响进行了拓展分析。切削三要素主要通过影响材料去除时的变形量及刀屑界面的摩擦力来影响切削比能。对切削比能影响最大的是进给量,其次是切削速度,背吃刀量对切削比能的影响最小。随着进给量的增大,切削比能降低。随着切削速度的升高,切削比能先增大后减小。背吃刀量的变化对切削比能影响不大,因此,从节能角度出发,在保证加工质量的前提下进行切削加工时,应选择大的进给量,小的背吃刀量,以及合适的切削速度。 本文为切削比能的计算提供了方法指导及理论基础,但尚需展开进一步探究:相同线速度在不同工件直径和主轴转速匹配环境下的变动情况尚需进一步探究,进而可结合机床运转功率建立机床层加工比能模型;为适应当今先进化高效化生产的需求,新工艺、新材料、新设备环境下的材料去除机理及切削比能数据尚待揭示和开发;保证加工质量及加工系统安全性前提下的节能参数优化分析尚待展开。 [1]MatthewB,GutowskiT,JonesA,etal.AThermodynamicFrameworkforAnalyzingandImprovingManufacturingProcesses[C]//IEEEInternationalSymposiumonElectronicsandtheEnvironment.SanFrancisco,USA,2008:212-217. [2]WarrenRD.AnalysisofMaterialRemovalProcess[M].NewYork,USA:Springer-verlag,1992. [3]Siemens.全面节能解决方案(TIES)[EB/OL]. [2012-02-24].http://www.doc88.com/p-810688757233.html. [4]DraganescuF,GheorgheM,DoicinCV.ModelsofMachineToolEfficiencyandSpecificConsumedEnergy[J].JournalofMaterialsTechnology,2003,141:9-15. [5]GutowskiT,DahmusJ,ThiriezA.ElectricalEnergyRequirementsforManufacturingProcesses[C]//13thCIRPInternationalConferenceonLifeCycleEngineering.Leuven,Belgium,2006:121-125. [6]GutowskiT.TheCarbonandEnergyIntensityofManufacturing[C]//40thCIRPInternationalManufacturingSystemsSeminar.Liverpool,UK,2007:23-32.[7]DiazN,RedelsheimerE,DornfeldD.EnergyConsumptionCharacterizationandReductionStrategiesforMillingMachineToolUse[C]//Proceedingsofthe18thCIRPInternationalConferenceonLifeCycleEngineering.Brauschweig,Germany,2011:263-267.[8]LiW,KaraS.AnExperimentalModelforEnergyConsumptionofManufacturingProcesses:aCaseofTurningProcess[J].JournalofEngineeringandManufacturing,2011,225:1636-1649. [9]PawadeRS.AnAnalyticalModeltoPredictSpecificShearEnergyinHigh-speedTurningofInconel718[J].InternationalJournalofMachineToolsandManufacture,2009,49:979-990. [10]AlessandroRR,ReginaldoTC.InfluenceofTheToolEdgeGeometryonSpecificCuttingEnergyatHigh-SpeedCutting[J].JournaloftheBrazilianSocietyofMechanicalSciencesandEngineering,2007,29(3):279-283. [11]陈日曜. 金属切削原理[M]. 北京:机械工业出版社,2008. [12]TaoPeng,XunXu.AUniversalHybridEnergyConsumptionModelforCNCMachiningSystems[C]//20thCIRPInternationalConferenceonLifeCycleEngineering.Singapore,2013:251-256. [13]UluerMU,KilicSE.AModelforPredictingTheoreticalProcessEnergyConsumptionofRotationalPartsUsingSTEPAP224Features[C]//20thCIRPInternationalConferenceonLifeCycleEngineering.Singapore,2013:141-146. [14]李涛,孔露露,张洪潮,等. 典型切削机床能耗模型的研究现状及发展趋势[J]. 机械工程学报,2014,50(7):102-111. LiTao,KongLulu,ZhangHongchao,etal.RecentResearchandDevelopmentofTypicalCuttingMachineTool’sEnergyConsumptionModel[J].JournalofMechanicalEngineering,2014,50(7):102-111. [15]施金良,刘飞,许弟建,等. 数控机床空载运行时节能决策模型及实用方法[J]. 中国机械工程,2009,20(11):1344-1346. ShiJinliang,LiuFei,XuDijian,etal.DecisionModelandPracticalMethodofEnergy-savinginNCMachineTool[J].ChinaMechanicalEngineering,2009,20(11):1344-1346. [16]滕素珍,冯敬海.数理统计学[M].大连:大连理工大学出版社,2005. (编辑郭伟) SCE Modeling and Influencing Trend Analysis of Cutting Parameters Zhang HongchaoKong LuluLi TaoChen Junchao Dalian University of Technology,Dalian,Liaoning,116024 This paper analyzed the energy consumption phenomenon with respect to the material removal mechanism and gave an empirical formula. An index formula was worked out based on the experimental data related to the facing processes performed on a turning machine. The influencing trends of cutting speed, feed rate and cutting depth on SCE were analyzed, which provides the basic indication for energy-saving machining parameters’ selection and low-carbon manufacturing assessment inventory requirements. material removal;cutting energy consumption;specific cutting energy(SCE);turning;lean production 2013-11-22 2015-01-15 国家自然科学基金资助项目(5127507);国家重点基础研究发展计划(973计划)资助项目(2011CB013406) TG511DOI:10.3969/j.issn.1004-132X.2015.08.019 张洪潮,男,1953年生。大连理工大学机械工程学院教授。研究方向为低碳制造、全生命周期分析。出版专著2部,发表论文150余篇。孔露露,女,1988年生。大连理工大学机械工程学院硕士研究生。李涛,女,1977年生。大连理工大学机械工程学院讲师。陈俊超,男,1989年生。大连理工大学机械工程学院硕士研究生。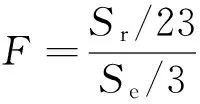

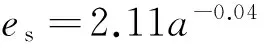
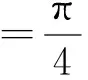
3 结论及展望
