基于蒙特卡洛模拟与响应面方法的公差建模
2015-10-28余治民刘子建董思科李斯明艾彦迪
余治民 刘子建 董思科 李斯明 艾彦迪
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
基于蒙特卡洛模拟与响应面方法的公差建模
余治民刘子建董思科李斯明艾彦迪
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
针对现有机床精度设计方法实用性不强的问题,提出了一种基于蒙特卡洛模拟与响应面方法的公差建模方法。采用基于数学定义的公差分析理论建立公差的变动不等式与约束不等式;运用蒙特卡洛模拟法进行仿真试验,模拟实际公差表面的变动,生成公差变动要素的实际变动区间;以公差与试验得到的公差变动要素实际变动区间带宽值为建模样本,运用响应面方法建立两者间的响应面模型;对一个典型实例进行分析,分析结果表明,该方法符合工程实际,具有较高的建模精度及技术经济性。
蒙特卡洛模拟;响应面法;小位移旋量;约束不等式;变动不等式
0 引言
科学技术的进步促使机床朝着高速和高精度方向发展,机床精度性能的设计与提高变得日益重要。国内外学者在机床精度设计领域开展了大量的研究,取得了一定的进展。文献[1-3]运用多体运动学理论建立了机床的误差传递模型;文献[4-5]分析了加载时工作零件的变形量,将其转变为雅可比旋量修正量, 通过对雅可比旋量公差模型在实际工况下的修正, 建立了基于雅可比旋量和实际工况的装配体公差数学模型;文献[6]给出了三维公差累积运动学模型的一般表示式,研究了该模型在公差优化设计中的应用。但上述研究都将机床零部件间的几何变量约束统一用6项公差变动要素(3项平动误差与3项转动误差)进行描述,而公差变动要素与零部件公差之间的关系并不明确,无法建立反映零部件公差与机床精度映射关系的数学模型,也就无法有效地对机床零部件公差进行合理分配,只能根据并不完善的公差模型来进行公差分配,可靠性低。因此,建立能用于工程实际且定义严格的公差模型,对机床的精度分析与分配研究具有重要意义。
公差建模的关键是可以对满足公差的公差变动要素作出正确的解释[7],即公差变动要素如何在公差域中变动。文献[8-10]运用基于数学定义的公差建模方法,用变动不等式和约束不等式严谨地描述了公差变动要素与公差间的关系,建立了不同类型公差的数学模型,但由于约束不等式中变动要素存在变动顺序不确定性,难以得到公差变动要素实际变动区间与公差间的具体函数关系,因此该模型无法用于直接指导精度设计。
本文以平面尺寸公差与平面度公差为研究对象,在深入研究基于数学定义的公差分析方法的基础上,将蒙特卡洛模拟与响应面方法应用于公差建模,考虑公差原则及约束条件等因素对公差变动要素的影响,建立变动要素实际变动区间带宽与公差间的响应面模型,以解决现有精度设计方法实用性不强的问题,并通过典型实例验证该方法的有效性。
1 基于小位移旋量的公差数学表示
三维空间中,物体表面可抽象为点、线、面等基本要素,并有3个沿坐标轴方向的平动自由度和3个绕坐标轴的转动自由度。用d=(u,v,w)和θ=(α,β,δ)分别表示平动与转动自由度的微小变动矢量,则这两组矢量组成的合成矢量D=(θ,d)=(α,β,δ,u,v,w)称为小位移旋量(smalldisplacementtorsors,SDT),α、β、δ、u、v、w为SDT的旋量参数。
公差域表示公差实际表面脱离名义表面变动的范围或区域,而物体表面的点、线、面等基本要素的变动量均可以通过各自的SDT表示。据此,Bourdet 在1996年首次将SDT引入到公差领域,提出了基于SDT的公差数学表示方法[11],即用旋量参数的变动来描述公差实际表面在公差域中的变动。旋量参数也称为公差变动要素。表1列出了几种形位公差对应的公差域和SDT。
2 基于蒙特卡洛模拟与响应面方法的公差建模
公差分为尺寸公差、形状公差和位置公差。针对尺寸公差和位置公差,分析时可以假设变动后公差实际表面的形状保持不变,即平面变动后依旧为平面,直线变动后依旧为直线,但对于形状公差,这一假设并不成立[12]。为此,本文从两类公差中各取一例,详细阐述基于蒙特卡洛模拟与响应面方法的公差建模步骤,其他类型的公差建模可依此类推。
2.1平面尺寸公差建模
2.1.1求解公差变动不等式与约束不等式
平面尺寸公差规定的公差域形式如图1所示。图中,TU、TL分别为上下偏差,公差T=TU+TL;D为基本尺寸;局部坐标系的z轴与平面法向平行。对于矩形平面,坐标系原点在平面中心位置;对于不规则平面,可用一等效矩形替代,则原点在等效矩形的中心位置。z=0表示名义公差平面;z(x,y)表示实际变动平面。由表1可知,变动平面z(x,y)对应的SDT为(α,β,0,0,0,w)T。尺寸公差用数学表示如下:
-TL≤z(x,y)≤TU
(1)
-(TL+TU)≤Δz(x,y)≤TL+TU
(2)

表1 不同类型公差及其对应的公差域和SDT
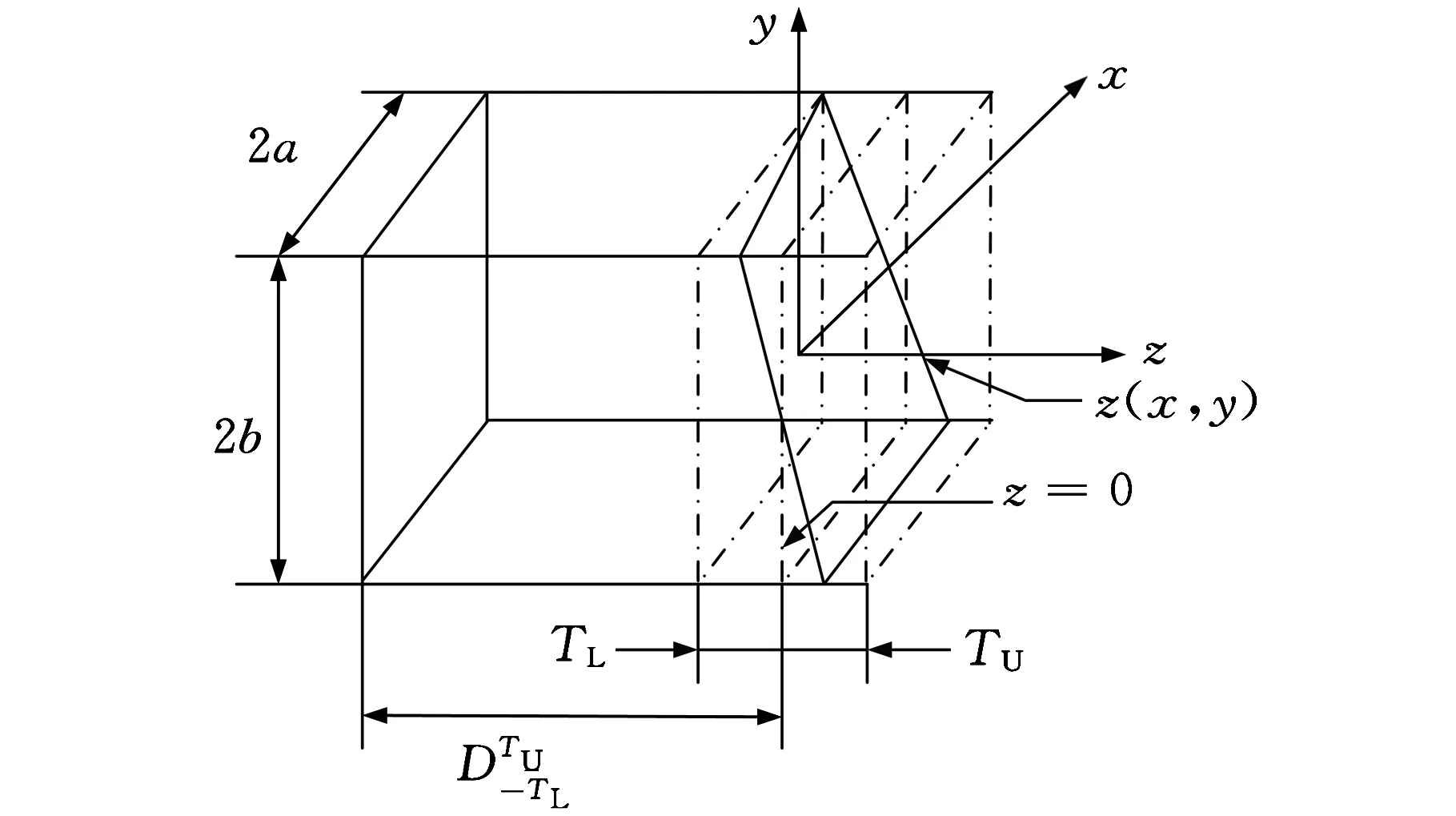
图1 平面尺寸公差域
其中,z(x,y)=dz+xβ+yα为实际变动平面方程,dz为实际变动平面中心点与参考坐标系原点在z方向上的位移;Δz(x,y)为变动平面z(x,y)上任意两点的z坐标值之差。由于变动后公差实际表面的形状保持不变,仍为矩形平面,极值情况必然发生在平面的4个顶点处,因此只需考虑变动平面顶点的z向坐标值是否在公差域内即可。
由图1可知,4个顶点的x、y向坐标分别为(a,b)、(-a,b)、(a,-b)、(-a,-b),由实际变动平面方程可知,4个顶点的坐标分别为
S1=(a,b,dz+aβ+bα)
S2=(-a,b,dz-aβ+bα)
S3=(a,-b,dz+aβ-bα)
S4=(-a,-b,dz-aβ-bα)
由式(1)可得
(3)
由式(2)、式(3)可得旋量参数的变动不等式[8]为
(4)
约束不等式[8]为
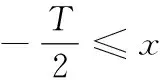
(5)
-TL≤w+xβ+yα≤TU
(6)
其中,x、y分别取4个顶点的x、y向坐标值。
变动不等式式(4)定义了旋量参数的理想变动区间。约束不等式的存在使旋量参数不可能同时取最大值,参数的实际变动区间比理想变动区间要小,如果按旋量参数的理想变动区间进行精度设计,则会提高零件加工精度的要求,增加制造成本。而旋量参数实际变动区间与公差间的具体关系尚不明确。
2.1.2蒙特卡洛模拟法求解旋量参数实际变动区间
蒙特卡洛模拟法也称为随机模拟方法,它以概率论和数理统计为基础,通过对随机变量的统计实验和随机模拟来求解问题近似解。由于多种因素综合作用的影响,产品公差实际表面变动的形式在公差域内是无法预知的,具有随机性,其分布的规律随加工条件而定,因此,与公差对应的SDT旋量参数也是随机量[13]。由式(4)~式(6)可知,旋量参数的变动顺序不同,其最终的取值也会不同。本文根据变动不等式和约束不等式,运用蒙特卡洛模拟法,按给定的参数分布类型和变动顺序进行模拟试验,生成相应的参数随机数,模拟实际公差表面的变动,对满足约束条件的随机数加以保留,不满足约束条件的则剔除,当产生足够多满足条件的随机数样本后,对样本进行分析,求解出对应旋量参数的变动区间带宽,再根据变动区间带宽和均值得到旋量参数的实际变动区间。求解步骤如下:
(1)根据研究对象的具体情况,确定旋量参数的理想概率分布模型。本文假定旋量参数的分布函数均为正态分布:
式中,μ、σ分别为正态分布的均值和均方差。
(3)根据抽样规则对旋量参数进行抽样。3个非零旋量参数共有6种变动顺序,为了尽可能地模拟零件的实际加工工况,对每一种变动顺序都进行抽样。以变动顺序α→β→w为例,其抽样流程如图2所示。
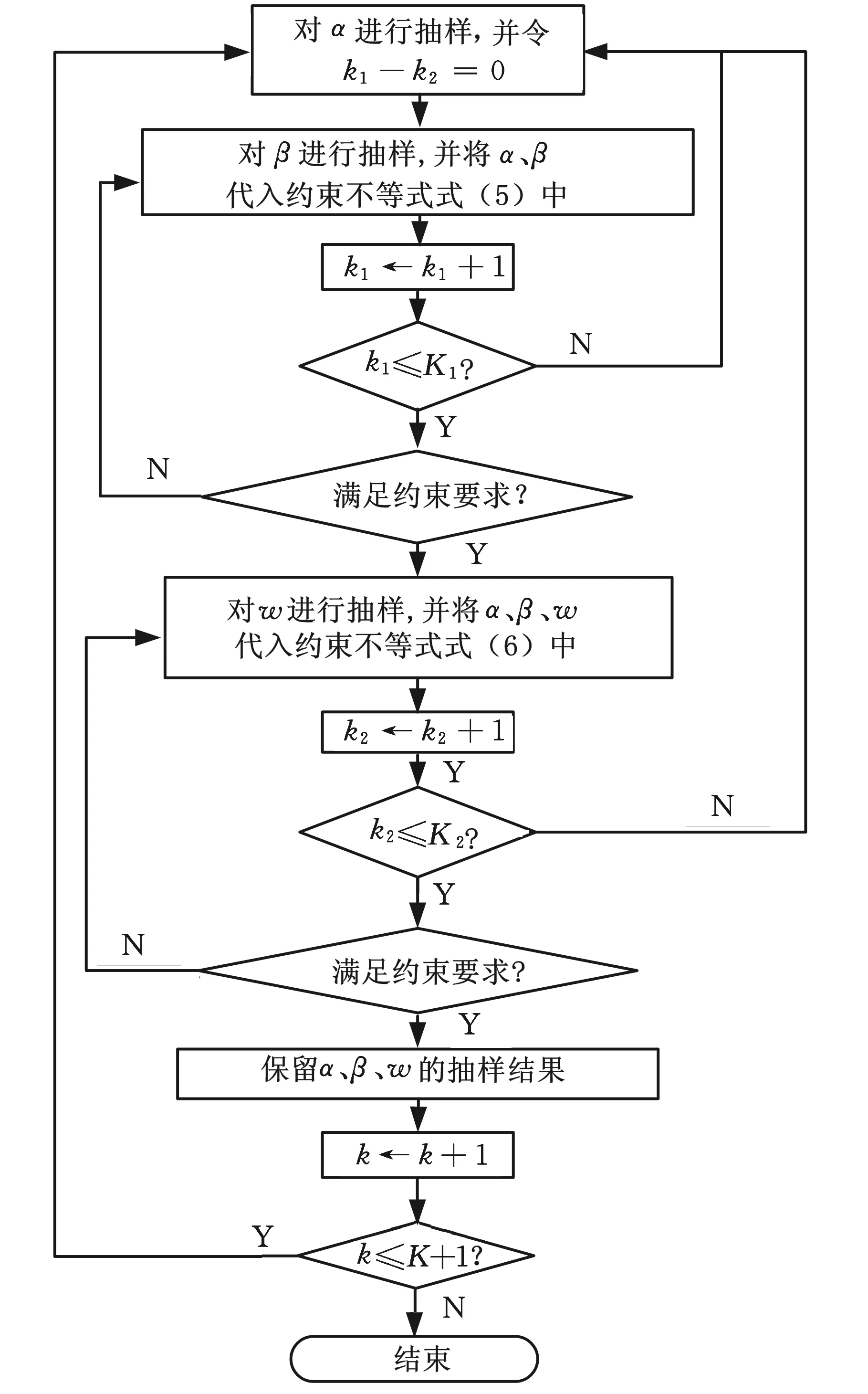
图2 抽样流程一
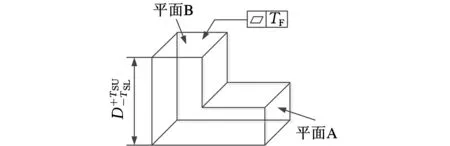
图2中,k的初始值为1;K为要求抽取的合格样本数,为保证模拟精度,K>20 000;K1、K2为常量,根据具体研究对象而定。设置判别式k1 按6种变动顺序编程进行抽样后,α、β、w均得到容量为6K的实际变动区间带宽样本。 (4)旋量参数实际分布函数的假设检验。由于约束不等式式(5)、式(6)的限制,旋量参数的实际分布类型并不一定与理想分布类型相同,故需对实际分布类型进行假设检验。本文采用χ3拟合检验法,以参数α为例,其基本思路为:在α分布未知时,先根据抽样获得的观测值对α的分布类型作出假设: H0∶F(α)=F0(α) 式中,F0(α)为假设的α分布函数。 将实数轴分为k个互不相交的区间(ai,ai+1](i=1,2,…,k),其中a1、ak+1可分别取-∞、+∞,区间的划分视具体情况而定。在假设H0下计算概率: pi=F(ai+1)-F(ai)=P(ai<α 计算理论频数。由于α的样本容量为6K,因此理论频数为6Kpi。 计算样本观察值落入区间(ai,ai+1]中的个数fi(i=1,2,…,k),fi称为实际频数。 计算统计量 当样本容量6K≥50时,统计量χ2近似服从自由度为k-r-1的χ2分布(r为确定F0(α)表达式中被估计参数的个数,如F0(α)为正态分布,则r=2)。 (5)采用极大似然估计法估计实际分布函数的参数。如果经第(4)步假设检验验证α也属于正态分布N(μ,σ2),则根据α的样本,采用极大似然估计法估计α分布函数的参数,得到μ与σ2的极大似然估计量为 由于变动不等式与约束不等式均具有对称性,故旋量参数实际分布的均值近似等于理想分布的均值。 (6)求解旋量参数的实际变动区间。根据参数的实际分布函数类型与均方差,查表得到参数的实际变动区间带宽: 其中,G表示相对分布系数,如果旋量参数为正态分布,则G等于1。旋量参数的实际变动区间为 2.1.3运用响应面法建立旋量参数实际变动区间带宽与公差间的响应面函数 响应面方法是数学方法与统计方法相结合的一种建模方法,主要用于解决如何建立复杂系统输入(变量)与输出(响应)之间近似函数关系的问题。其基本思路是,依据试验设计原则选定设计空间中的试验点,用多组试验点及其对应的响应值拟合响应面曲面,从而构造具有明确表达形式的显式函数[14-15]。 通过前文分析可知,只要确定了旋量参数实际变动区间带宽即可确定参数的实际变动区间。对于任意的平面尺寸公差均可通过蒙特卡洛模拟法得到与之对应的旋量参数实际变动区间带宽的响应值,但两者间的函数关系并不明确,无法用严格的数学公式表达。为此,本文采用响应面方法,建立公差与旋量参数实际变动区间带宽间的响应面模型,进而确定公差与旋量参数实际变动区间之间的响应关系,为后续的精度分析与精度分配研究打下基础。建模的步骤如下: Fy=c0+c1T+c2T2y=α,β,w 式中,ci(i=0,1,2)为待求系数。 采用最小二乘法求解C=[c0c1c2]T的无偏估计: (3)验证模型精度。响应面生成后,采用复相关系数R2对响应面模型进行验证,其表达式为 复相关系数R2代表了响应面预测值与真值之间的差异程度,在0~1之间取值,值越大,表示差异度越小。 2.2平面度公差建模 形位公差数学建模的目的是确定形位公差域边界的变动范围及公差变动要素的表示方法。由工程实践可知,对某几何要素给出形位公差的原因是:当其他的公差(如尺寸公差)存在,但仍不能满足对几何要素形位变动限制的要求时,需要给出公差值较小的形位公差来进一步限制。实际上,尺寸公差与形位公差是同一实际几何要素反映的两种不同概念的公差,是同一问题的两个方面。因此,在研究形位公差的建模时不能离开尺寸公差而单独处理,需要进一步研究形位公差与尺寸公差的关系,即要考虑公差原则。 由GB4249-1996可知,公差原则包含独立原则和相关要求,相关要求中又分为包容要求、最大实体要求和最小实体要求。本文以独立原则为例,对平面度公差进行建模。 2.2.1求解平面度公差变动不等式与约束不等式 由平面度的定义可知,若平面度大小为TF,则平面上所有的点均必须位于距离为TF的两平行平面所形成的公差域内。用Bottom和Top分别表示两平行平面,Bottom面表示材料边内的平面,Top面表示材料外的平面,平面度公差规定的形式如图3所示。 (a)平面度公差 (b)平面度公差域图3 平面度公差及其公差域 图3中,+TSU、-TSL分别表示尺寸公差TS的上下偏差;TF表示平面度公差;平面A为基准平面,平面B为变动平面。设Bottom与Top平面对应的SDT分别为(αB,βB,0,0,0,wB)T、(αT,βT,0,0,0,wT)T,则Bottom面和Top面的变动方程分别为 zB=wB+xβB+yαB zT=wT+xβT+yαT= 由独立原则可知,平面B必须在尺寸公差域(ST域)内,即与平面A相距D-TSL~D+TSU的区域。此时,对平面度公差域(FT域)的唯一限制是在FT域内存在一个平面,它同时也在ST域。采用基于数学定义的公差分析方法求解得到Bottom面旋量参数的变动不等式为 (7) 约束不等式为 -TSL-TF≤xβB+yαB≤TSU (8) -TSL-TF≤wB+xβB+yαB≤TSU (9) 其中x、y分别取Bottom面4个顶点的x、y向坐标值。 由于Bottom面和Top面互相平行,故有 αT=αB,βT=βB,wT=wB+TF (10) 通过式(7)~式(10)确定了Bottom和Top面的变动范围,但变动平面在Bottom和Top面限制的区域中如何分布并不确定。为此,本文采用二元线性回归法求解变动平面旋量参数的值,其基本思路如下:已知Bottom和Top面的方程,在名义平面内设置m×n个取样点,使之成m×n网格分布,通过随机模拟法对每个取样点在Bottom和Top面限制的范围内取z值,这样就得到Q(Q=m×n)个平面度区域内的模拟点。根据Q个模拟点的值,采用二元线性回归算法计算得到变动平面旋量参数的值。旋量参数的表达式如下: 2.2.2蒙特卡洛模拟法求解旋量参数实际变动区间 由于可以假设变动后公差实际表面的形状保持不变,故用蒙特卡洛模拟法求解尺寸公差旋量参数实际变动区间时,通过模拟抽样得到的旋量参数值即可作为公差的实际旋量参数。与尺寸公差不同之处在于,形状公差只确定了公差特征要素的分布区域,通过蒙特卡洛模拟法抽样只能确定公差特征要素分布区域的上下边界(即Bottom和Top面),而特征要素在区域内如何分布仍不确定,需要再采用二元线性回归法求解公差的实际旋量参数。求解步骤如下: (1)根据研究对象的具体情况,确定旋量参数的理想概率分布模型。本文假定旋量参数的分布函数均为正态分布: (2)根据Bottom面变动不等式式(7)确定各旋量参数理想分布的均值与方差。由式(7)可知,旋量参数αB、βB、wB理想分布的均值与方差分别为 (3)根据抽样规则对旋量参数进行抽样。Bottom面的3个非零旋量参数同样有6种变动顺序,需对每一种变动顺序都进行抽样。以变动顺序αB→βB→wB为例,其抽样流程如图4所示。 图4 抽样流程二 按6种变动顺序进行抽样后,α、β、w均得到容量为6K的实际变动区间带宽样本。 第(4)~(6)步与2.1.2节所述过程相似,在此不再重复阐述。 2.2.3运用响应面法建立旋量参数实际变动区间带宽与公差间的响应面函数 由式(7)可知,与尺寸公差响应面方法建模的不同之处在于,平面度公差建模过程中包含尺寸公差和平面度公差2个设计变量,需同时考虑这两者对变动区间带宽的影响,建模的步骤如下: 式中,ci(i=0,1,…,4)为待求系数。 采用最小二乘法求解C=[c0c1c2c3c4]T的无偏估计 (3)验证模型精度。与2.1.3节所述过程相似,在此不再重复阐述。 图5 α变动区间带宽 图6 β变动区间带宽 图7 w变动区间带宽 令下降比例等于残余带宽除以理想变动区间带宽。下降比例均值为100个试验点对应的下降比例的均值。下降比例均值反映了将蒙特卡洛模拟法应用于精度设计时对提高精度设计技术经济性的效果。表2列出了3个旋量参数实际变动区间带宽下降比例均值。 表2 实际变动区间带宽下降比例均值 % 由表2可知,在考虑约束条件及参数变动顺序后,运用蒙特卡洛模拟法求解得到的旋量参数实际变动区间带宽较理想变动区间带宽下降比例的均值分别为22.49%、22.85%、20.34%,说明采用蒙特卡洛分析方法可以显著提高精度设计的技术经济性,且更加符合零件生产实际。 Fα=0.0026+0.024TS+ Fβ=0.0014+0.188TS+ Fw=0.0657+0.57TS+ 用复相关系数R2验证3个响应面模型的精度,如表3所示。由表3可知,3个响应面模型的R2值均大于0.985,表明本文建立的公差响应面 表3 响应面模型的R2检验 模型具有很高的精度。 本文将蒙特卡洛模拟法良好的求解非确定性问题的能力与响应面方法优秀的建模性能结合起来,提出了一种基于蒙特卡洛模拟与响应面方法的公差建模方法。在对平面尺寸和形状公差域变动关系进行深入研究的基础上,采用蒙特卡洛模拟法求解公差与公差变动要素变动区间之间的响应关系,再运用响应面方法建立了两者之间的响应面数学模型。以平面度公差建模为例,验证了该方法可以显著提高精度设计的技术经济性。进一步将该方法应用到机床的精度设计当中,对提高机床精度设计方法的实用性,降低机床的生产成本具有重要意义。 [1]刘又午.多体动力学的休斯敦方法及其发展[J].中国机械工程,2000,11(6):601-608. Liu Youwu.Development of Huston’s Method on Multibody Dynamics[J].China Mechanical Engineering,2000,11(6):601-608. [2]Chen J S.Computer-aided Accuracy Enhancement for Multi-axis CNC Machine Tool[J].International Journal of Machine Tools and Manufacturing,1999,35(4):593-605. [3]Patel A J,Ehmann K F.Volumetric Error Analysis of a Stewart Platform-based Machine Tool[J].Annals of the CIRP,1997,46(1):287-290. [4]Laperriere L,Ghie W,Desrochers A.Statistical and Deterministic Tolerance Analysis and Synthesis Using a Unified Jacobian-Torsor Model[J].CIRP Annals-Manufacturing Technology,2002,51(1):417-420. [5]张为民,李国伟,陈灿.基于雅可比旋量理论的公差优化分配[J].农业机械学报,2011,42(4):216-219. Zhang Weimin,Li Guowei,Chen Can.Optimal Allcocation of Tolerance Based on Jacobian-Torsor Theory[J].Transactions of the Chinese Society for Agricultural Machinery,2011,42(4):216-219. [6]胡洁,吴昭同,杨将新.基于旋量参数的三维公差累积的运动学模型[J].中国机械工程,2003,14(2):127-130. Hu Jie,Wu Zhaotong,Yang Jiangxin.Kinematic Model of 3D Tolerance Accumulation Based on Screw Parameter[J].China Mechanical Engineering,2003,14(2):127-130. [7]Mujezinovic A, Davidson J K, Shah J J. A New Mathematical Model for Geometric Tolerances as Applied to Polygonal Faces[J]. Transections of the ASME,2004,126(3):504-518. [8]刘玉生,吴昭同,杨将新,等.基于数学定义的平面尺寸公差数学模型[J].机械工程学报,2001,37(9):12-17. Liu Yusheng,Wu Zhaotong,Yang Jiangxin,et al.Mathematical Model of Size Tolerance for Plane Based on Mathematical Definition[J].Chinese Journal of Mechanical Engineering,2001,37(9):12-17. [9]Roy U,Li B.Representation and Interpretation of Geometric Tolerances for Polyhedral Objects Form Tolerances[J].Computer Aided Design,1998,30(2):151-161. [10]蔡敏,杨将新,吴昭同.平面要素公差数学定义理论及应用的研究[J].中国机械工程,2002,13(2):128-130. Cai Min,Yang Jiangxin,Wu Zhaotong.Theory and Application of Mathematical Definition for Plane Element Tolerance[J].China Mechanical Engineering,2002,13(2):128-130. [11]Vignat F,Villeneuv F.3D Transfer of Tolerances Using a SDT Approach:Application to Turning Process[J].Journal of Computing and Information Science in Engineering,2003,3(3):45- 53. [12]Shah J J.Dimension and Tolerance Modeling and Transformations in Feature Based Design and Manufacturing[J].Journal of Intelligent Manufacturing,1998(9):475-488. [13]Zhong Xin,Yang Ruqing,Zhou Bing.Accuracy Analysis of Assembly Success Rate with Monte Carlo Simulations[J].Journal of Donghua University,2003,20(3):128-131. [14]Kim S H,Na S W.Response Surface Method Using Vector Projected Sampling Points[J].Structrual Safety,1997,19:3-19. [15]Kaymaz I,Mcmahon A.A Response Surface Method Based on Weighted Regression for Structural Reliability Anslysis[J].Probabilistic Engineering Mechanics,2004,20:11-17. (编辑苏卫国) Tolerance Modeling Based on Monte-Carlo Simulation and Response Surface Method Yu ZhiminLiu ZijianDong SikeLi SiminAi Yandi State Key Laboratory of Advanced Design and Manufacture for Vehicle Body,Hunan University,Changsha,410082 For the poor practicability of existing precision design method of machine tool,a new method about tolerance modeling based on MCS and response surface method was proposed herein.Firstly,the constraint inequality and change inequality were established using tolerance analysis based on mathematic definition theory.And then the simulated tests with MCS method were conducted to simulate the change of actual tolerance surface,and get the actual change interval of the tolerance factor.With the samples based on the tolerance and the bandwidth value of actual change interval obtained above,the response surface modeling between the tolerance and bandwidth was constructed by response surface method.Finally,a typical example was analyzed and the results indicate the method is consistent with engineering practice, and has high modeling precision and technical economics. Monte-Carlo simulation(MCS);response surface method;small displacement torsor;constraint inequality;change inequality 2013-06-21 国家自然科学基金资助项目(51175161,51301532);国家科技重大专项(2011ZX04003-011) TH115DOI:10.3969/j.issn.1004-132X.2015.04.001 余治民,男,1984年生。湖南大学汽车车身先进设计制造国家重点实验室博士研究生。研究方向为复杂装备精度链设计方法。刘子建,男,1953年生。湖南大学汽车车身先进设计制造国家重点实验室教授、博士研究生导师。董思科,男,1986年生。湖南大学汽车车身先进设计制造国家重点实验室硕士研究生。李斯明,男,1988年生。湖南大学汽车车身先进设计制造国家重点实验室硕士研究生。艾彦迪,男,1982年生。湖南大学汽车车身先进设计制造国家重点实验室助理研究员。
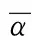
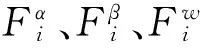
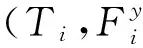



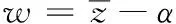
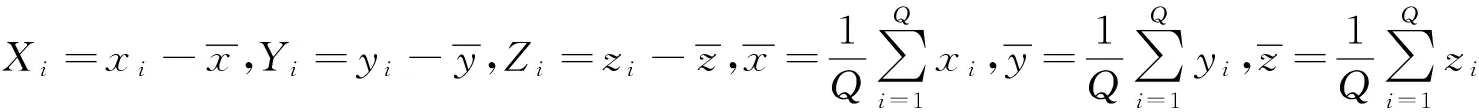



3 实例分析
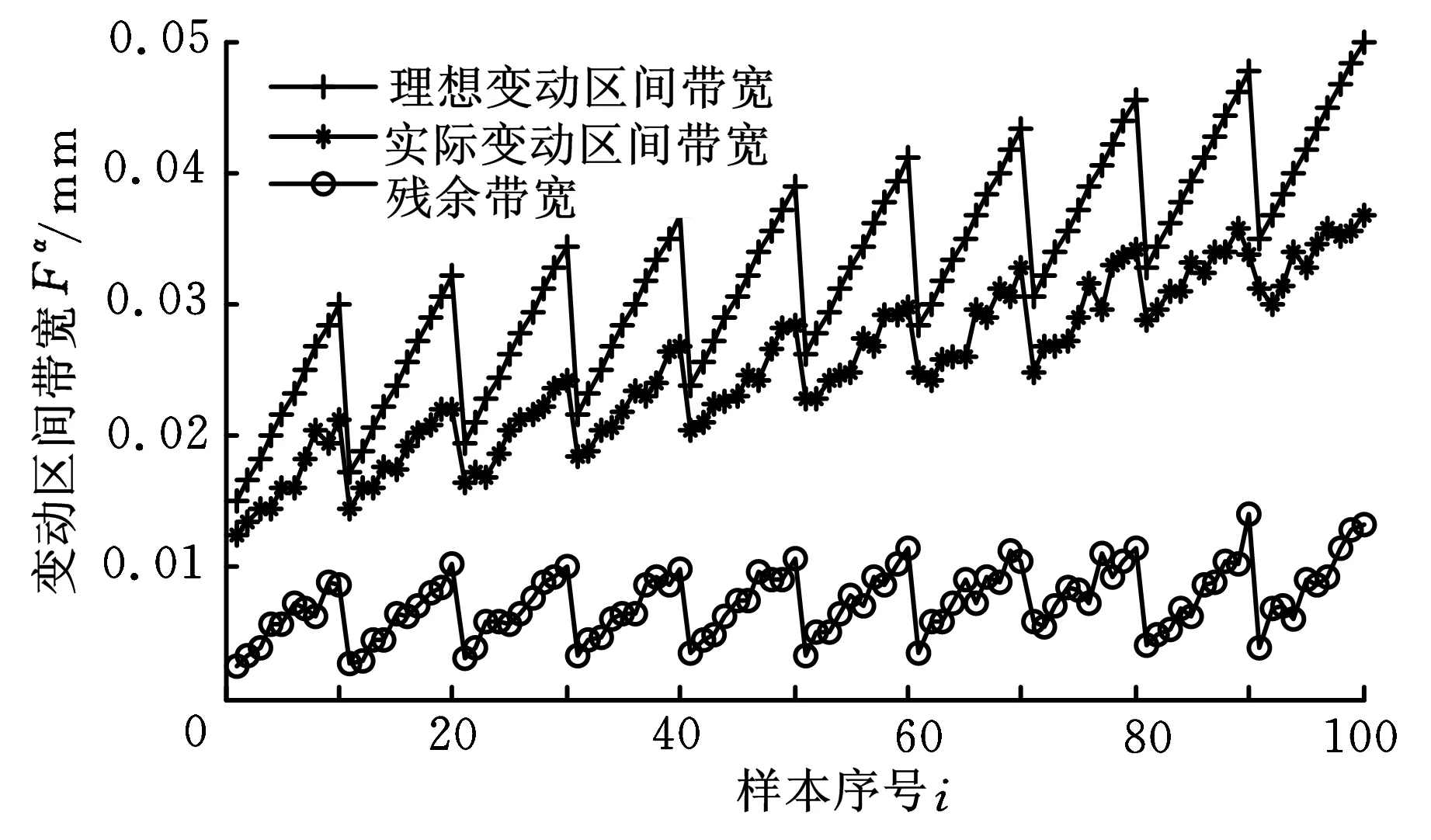
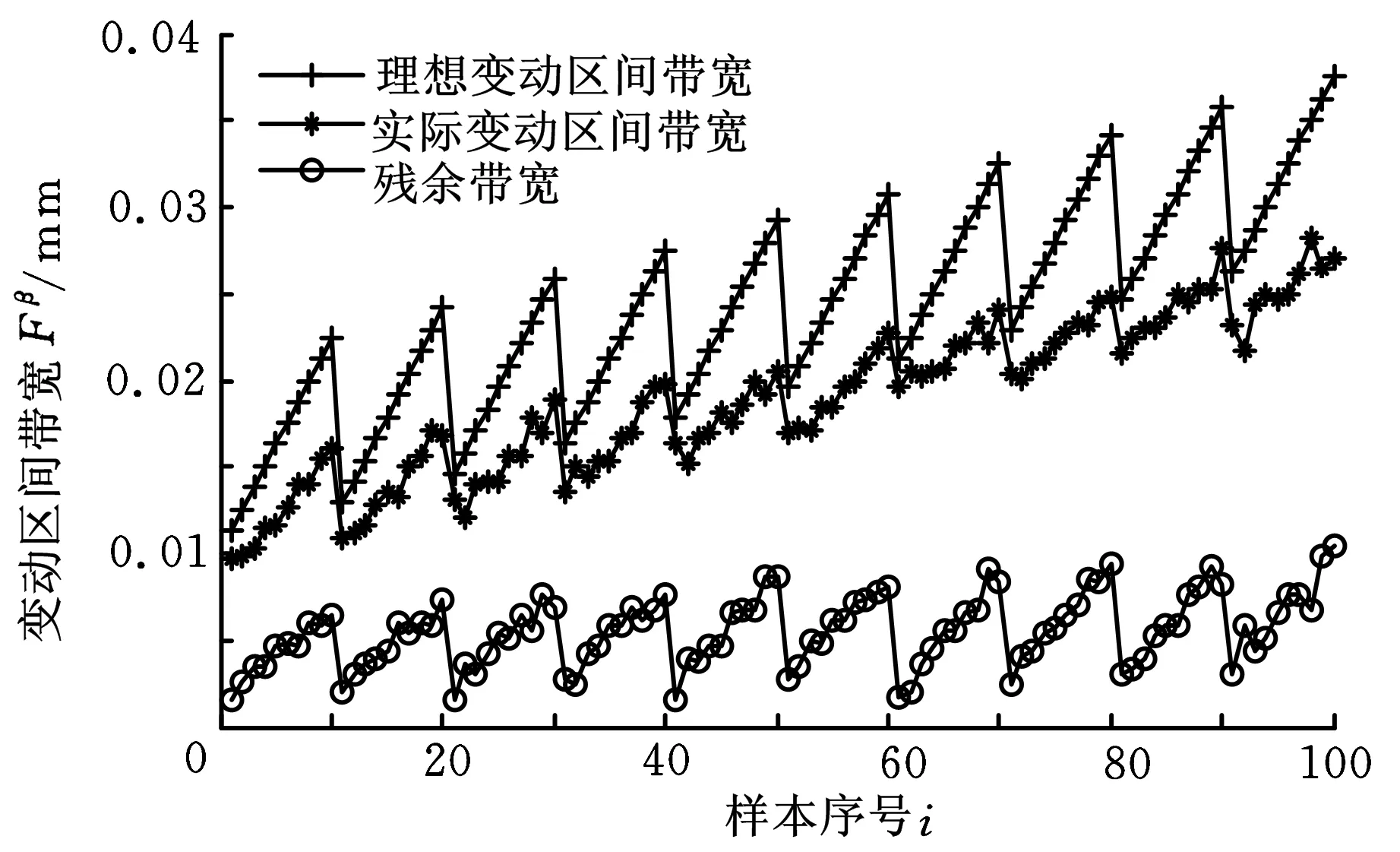
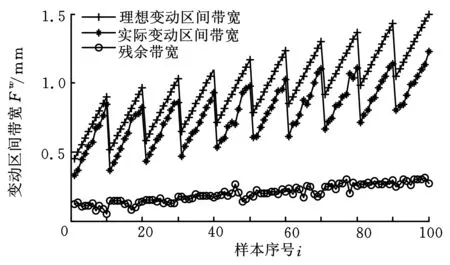

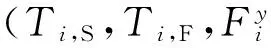

4 结语
