基于交集运算的自由度快速求解方法

卢文娟　张立杰　张一同

1.先进锻压成形技术与科学教育部重点实验室,秦皇岛,0660042.燕山大学河北省重型机械流体动力传输与控制重点实验室,秦皇岛,066004

基于交集运算的自由度快速求解方法

卢文娟1,2张立杰1,2张一同1,2

1.先进锻压成形技术与科学教育部重点实验室,秦皇岛,0660042.燕山大学河北省重型机械流体动力传输与控制重点实验室,秦皇岛,066004

为简化机构自由度计算，基于GOM公式和杆组位移参数求交，通过分析平行约束力的位置关系判断基点转动参数的有效性，给出并证明了转动不受约束的3种情况，为有效解决集合求交运算中的转动参数是否被约束问题，以及机构自由度快速计算和自由度运动性质判别提供了一种简洁实用的方法。以3种典型机构为例，对基点参数有效性判别和机构自由度快速计算进行了验证。

自由度；快速求解；集合求交；过约束

0　引言

机构自由度计算是机构分析的最基本问题。在机构自由度研究近160年的历史中，产生了几十种具有代表性的自由度计算公式，但这些公式中的大多数在求解某些含有过约束的机构时，其直接计算结果与实际不符[1]，原因在于没有正确考虑机构中的过约束。当机械系统中对同一构件提供有两个或以上作用效果相同的约束时，便产生了过约束。对过约束的处理是机构自由度计算的关键，同时也是进行机构自由度计算要解决的瓶颈问题。

机构过约束处理方法大致分为两类：一类是在公式中加入过约束的项进行过约束处理的方法，如黄真等提出的修正的K-G公式[1-3]；另一类是从避开过约束角度考虑的机构自由度快速求解处理方法，文献[4-9]为这方面具有代表性的研究成果。

在机构学不断更新的过程中，如何将自由度计算尽量浅显地表达出来，使其更容易为普通技术人员所理解具有重要的实际意义。本文以交集计算避开过约束为前提，基于GOM公式[10]介绍一种涉及机构转动问题的自由度计算方法。

1　自由度快速求解方法

1.1GOM公式

以揭示机构自由度、广义杆组和输出参数三者的内在关系且避开过约束为目的，基于广义杆组自由度和基点参数等新概念，建立了一种新的自由度公式——GOM公式。这里定义每个独立环路与其相邻环路不重复的独立杆件的组合为广义杆组，简称为杆组。杆组在空间坐标系中位移的向量表达形式为

(1)

由n个杆组位移参数组成的矩阵称为位移参数矩阵，其表达式为

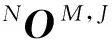
由L个独立环路组成的机构，其自由度数目为

(2)

式(1)和式(2)合称为GOM公式。

1.2自由度快速求解方法的基本思想

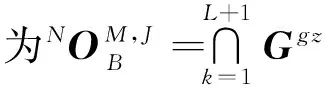
以图1所示机构为例，介绍并推导基点角位移参数有效性的判断原理。在图1的两机构中，两杆组组成分别相同，图1a中的2个分支Z方向轴线不重合，而图1b中的2个分支Z方向轴线重合。

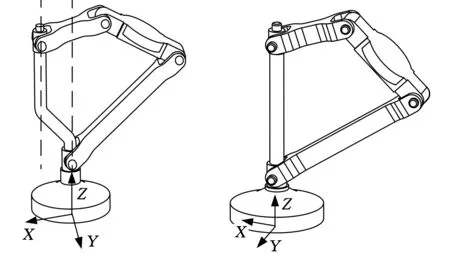
(a)F=1，一个转动自由度(b)F=2，2个转动自由度图1　(Z)U(Y)R(Y)-(Z)U(Y)R(Y)机构

图1中的2个机构在图示坐标轴方向中的位移参数矩阵均为

表示2个杆组中均存在2个沿Y方向的约束力。不考虑组成并联机构的2个杆组的轴线关系对基点参数的影响，直接求交集得到的基点参数可记为

2个杆组参数中均存在沿Z方向的转动角位移，而基点参数中对应的γ是否有效，取决于Y方向的平行约束力是否约束Z方向的转动。

结合螺旋理论中约束螺旋和运动螺旋的互易积为零[11]的思想，分析平行约束力(不失一般性地设为Y方向)对转动(设为Z方向)的约束关系。

对于n(n≥2)个同方向的平行约束力构成的几何关系可能为：共轴、共面平行或空间平行。

(1)平行约束力共轴时，其最大线性无关数为1，仅约束沿着约束力方向的移动，不会约束任何转动。

(2)平行约束力共面时，首先写出由该n个Y方向约束力组成的约束螺旋系。为使得螺旋形式简单，沿其中一个约束力方向建立坐标系，使其通过坐标系的原点，其约束螺旋系的一般表达形式为

(3)

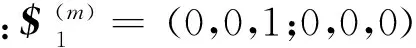
(3)约束力空间平行时：首先写出由该n个Y方向约束力组成的约束螺旋系。为使得螺旋形式简单，沿着其中一个约束力方向建立坐标系，使其通过坐标系的原点，其约束螺旋系的一般表达形式为

(4)

式(4)中第一个和第二个约束螺旋表示2个共面的Y方向约束力，a，c，e可任意选取。由于是空间约束力系，则d和f中至少有一个不为零。对式(4)求其反螺旋，则可得到运动螺旋系的表达式：

(5)

该螺旋系表示具有绕Y方向的转动以及沿X和Z方向的移动，而Z方向的转动是被约束的。

综上所述可知，某轴线方向的转动不受约束，存在以下三种情况：

情况一：杆组中有平行约束力存在，但平行约束力共线，其垂直方向的轴线转动不被约束。

情况二：杆组中有平行约束力存在，但平行约束力共面，则垂直于平行约束力而与约束力平面共面的轴线转动不被约束。

情况三：杆组中不存在垂直于某转动轴线方向的平行约束力，则该轴线方向的转动不被约束。

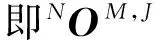
1.3自由度快速求解方法的步骤和特点

建立在位移参数矩阵基础上的本文自由度快速求解方法，只需简单判断转动垂直方向上平行约束力的位置关系即可进行求解。其求解流程图如图2所示。

图2　基于集合求交自由度求解流程图

基于以上三种情况进行集合求交计算自由度的方法具有如下特点：

(1)用α、β、γ、x、y、z6个元素描述各杆组的位移特征，可以直接表达各杆组的移动轴线和转动轴线方向。

(2)采用“集合求交”避开了机构过约束计算。

(3)将组成机构的各杆组作为一个单元，用杆组的位移参数向量去描述杆组的运动，而非单独描述某单个运动副的运动。

(4)用机构中各杆组的位移特征并行求交处理取代将各个杆组依次叠加进行交集运算的处理方式，以避开环路数目较多的机构带来的计算上的不方便。

(5)杆组位移参数表示杆组对动平台提供的约束的性质和约束力(偶)的方向；利用杆组的广义自由度进行机构的自由度表示，体现了各杆组对输出构件的约束作用。

(6)将螺旋理论思想应用于求交集计算和判断同方向约束力对垂直方向转动的约束，解决了转动求交不便的问题。

2　求解实例

为将上述提到的机构具有某轴线方向转动，且不受约束的三种情况应用到交集运算中，现以三种代表性的典型机构为例，进行机构自由度快速计算，并验证机构平台转动与平行约束力的关系。

例1：没有平行约束力的求交集问题。

图3所示为黄真等[12]于2000年发明的一个完全对称的4-URU并联机构，它由4个相同的URU分支同时连接上下平台构成。分支中的第一个是虎克铰，即U副，第二个是转动副R，第三个也是U副。每个URU分支相当于包含了5个单自由度的转动副，其中间转动副R两侧的两个转动副是相互平行的，且第一个转动副与基面相垂直，第5个转动副与运动平台相垂直，起始时上下平台平行。

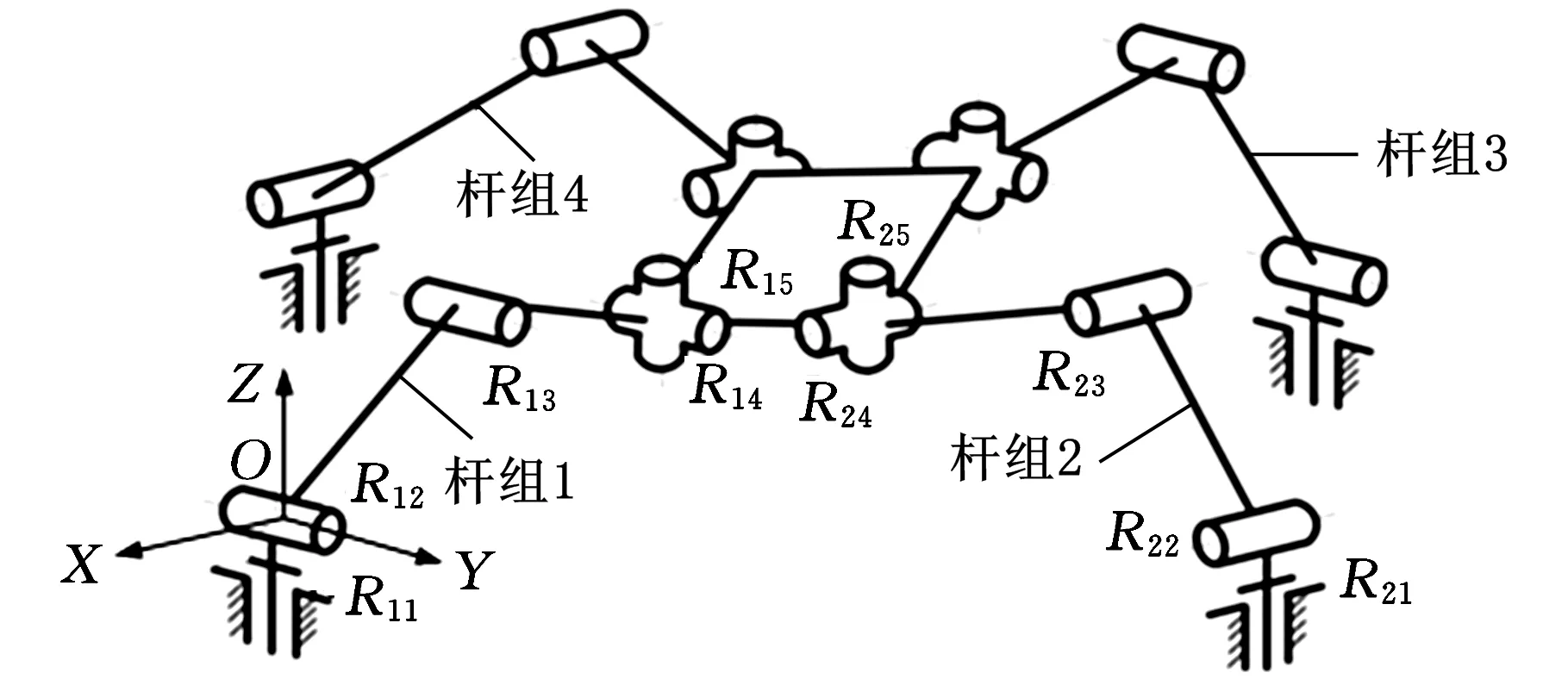
图3　4-URU机构

根据图2流程进行的图3机构自由度计算步骤如下：

(1)验证R12和R22轴线共面不平行时，其轴线是否垂直，且不影响计算结果。令R12和R22轴线垂直，并分别以R12和R22的轴线方向为坐标轴的X方向和Y方向(图3)，则机构的位移参数矩阵可表示为

各杆组的位移参数及杆组的阶可分别表示为

(2)不考虑转动是否被约束，通过直接求交集得到基点参数。其表达式为

(3)基点参数中仅有Z方向的角位移参数，且在垂直于Z轴方向上没有平行约束力，根据1.2节中的情况三，即γ为有效参数，则

(4)根据GOM公式(式(1)),求得的各杆组的广义自由度为

将数值代入GOM公式(式(2))。求得的机构自由度数为

例2：约束力共线时的求交集问题。

图4所示为对称的五自由度并联机构，它由3个相同的RR(RRR)分支同时连接上下平台。RR(RRR)表示分支由5个转动副构成，括号中的3个R表示转动副的轴线交于一个中心点，即3个分支的3个中心点重合于一个共同的中心点。每个分支的前2个转动副平行且垂直于基面[13]。

图4　3-RR(RRR)并联机构

(1)为使得到的杆组参数最少，以汇交中心为坐标轴原点，以Ri1轴线方向为Z轴方向建立坐标系，得到的机构位移参数矩阵为

各杆组的位移参数及杆组的阶分别为

(3)基点参数中存在3个角位移参数，且在Z方向上存在3个相平行的约束力，且3个约束力的作用点均作用在汇交中心，即3个约束力共线，满足1.2节中介绍的情况一，即存在一个公共约束，但不对任何转动产生约束，基点参数中不存在无效参数。其数学表达式为

(4)根据GOM公式计算的各杆组的广义自由度为

计算的机构自由度为

例3：转动受平行约束力约束的求交集问题。

图5所示为一3分支S/PRS/PSS非对称并联机构[14]，机构的上下平台都是三角形。机构杆组1中仅有一个球副，杆组2是5自由度PRS运动链，杆组3是7自由度PSS运动链，为无约束分支，不对动平台产生约束。

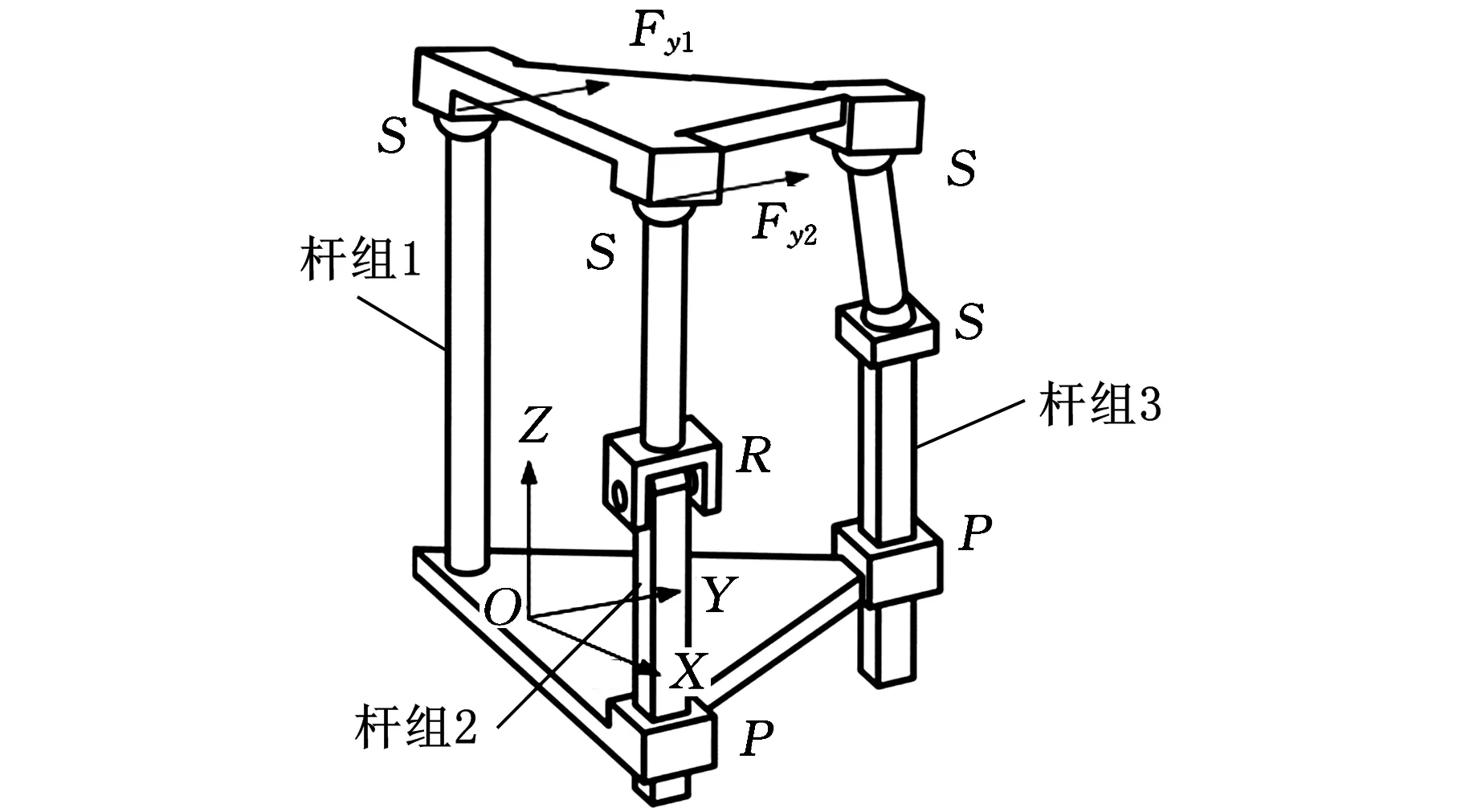
图5　S/PRS/PSS非对称并联机构

(1)为使得到的杆组参数最少，以转动副R的轴线方向为Y轴。得到的机构位移参数矩阵表达式为

各杆组的位移参数及杆组的阶分别为

(3)基点参数中存在3个角位移参数，且在Y方向上存在2个相平行的约束力。2个约束力的作用点分别在杆组1和杆组2的球副中心(图5)，不满足1.2节中介绍的三种情况，不能构成过约束，但会约束动平台的一个转动，即约束两力所决定的平面法线方向的转动，使得基点参数中角位移参数γ成为无效参数，即

(4)根据GOM公式计算的各杆组的广义自由度为

计算的机构自由度为

3　结论

为简化机构自由度计算，本文基于GOM公式和杆组位移参数求交法，以及螺旋理论分析了平行约束力的三种位置关系，结合基点转动参数的有效性，给出了转动不受约束的三种情况：

(1)杆组中有平行约束力存在，但平行约束力共线，其垂直方向的轴线转动不被约束。

(2)杆组中有平行约束力存在，但平行约束力共面，则垂直于平行约束力而与约束力平面共面的轴线转动不被约束。

(3)杆组中不存在垂直于某转动轴线方向的平行约束力，则该轴线方向的转动不被约束。

基于本文三种情况的机构自由度计算方法，可有效解决集合求交运算中的转动参数有否被约束的问题，为机构自由度快速计算和自由度运动性质判别提供了一种简洁、实用的方法。同时也为机构自由度的深入研究和复杂机构自由度的化简分析开辟了新的途径。

[1]GoguG.MobilityofMechanisms:aCriticalReview[J].Mech.Mach.Theory,2005, 40(9): 1068-1097.

[2]黄真. 论机构自由度——寻找了150年的自由度通用公式[M].北京:科学出版社,2011.

[3]LiuJingfang,HuangZhen.MobilityAnalysisofSomeParadoxicalMechanismsUsingaGeneralMethodology[C]//Proceedingsof2008ASMEInternationalDesignEngineeringTechnicalConferences.NewYork:ASME,2008:1421-1426.

[4]GoguG.MobilityandSpatialityofParallelRobotsRevisitedviaTheoryofLinearTransformations[J].EuropeanJournalofMechanics-A/Solids, 2005, 24(4): 690-711.

[5]GoguG.BifurcationinConstraintSingularitiesandStructuralParametersofParallelMechanisms[J].Meccanica，2011，46(1)：65-74.

[6]RicoJM,GallardoJ,RavaniB.LieAlgebraandtheMobilityofKinematicChains[J].JournalRoboticSystems, 2003, 20(8): 477-479.

[7]杨廷力,刘安心. 机器人机构拓扑结构设计[M]. 北京:科学出版社, 2012.

[8]ZhangYitong,MuDejun.NewConceptandNewTheoryofMobilityCalculationforMulti-loopMechanisms[J].Sci.ChinaTech.Sci., 2010, 53(6): 1598-1604.

[9]ZhangYitong,LiYanwen,WangLiya.ANewFormulaofMechanismMobilityBasedonVirtualConstraintLoop[J].Sci.ChinaTech.Sci., 2011, 54(10): 2768-2775.

[10]ZhangYitong,LuWenjuan,MuDejun,etal.ANovelMobilityFormulaforParallelMechanismsExpressedwithMobilityofGeneralLink-group[J].ChineseJournalofMechanicalEngineering, 2013,26(6):1082-1090.

[11]黄真，赵永生，赵铁石. 高等空间机构学[M].北京:高等教育出版社, 2006.

[12]HuangZhen,LiQinchuan.GeneralMethodologyforTypeSynthesisofLower-mobilitySymmetricalParallelManipulatorsandSeveralNovelManipulators[J].InternationalJournalofRoboticsResearch, 2002, 21(2): 131-145.

[13]黄真, 李秦川. 五自由度全对称运动解耦并联机器人机构:中国,ZL01122274.3[P]. 2002-02-13.

[14]ZengDaxing,HuangZhen,LuWenjuan.AFamilyofNovel2DOFRotationalDecoupledParallelMechanisms[C]//Proceedingsof2007InternationalConferenceonMechatronicsandAutomation.Harbin,China, 2007:2478-2483.

(编辑何成根)

Fast Solution Method of Mobility Calculation Based on List Intersection

Lu Wenjuan1,2Zhang Lijie1,2Zhang Yitong1,2

1.Key Laboratory of Advanced Forging & Stamping Technology and Science,Ministry of Education of China, Yanshan University,Qinhuangdao,Hebei,066004 2.Hebei Key Laboratory of Heavy Mechinery Fluid Power Transimission and Control,Yanshan University,Qinhuangdao,Hebei,066004

In order to express DOF calculation as simple as possible, based on the GOM formula and the intersection calculation of displacement parameters of general link group, three cases were presented and proved when the rotation was not as constrained. These cases were proposed by analyzing the relationship of parallel constrain forces to judge the validity of base point parameters. Therefore, the problem of the validity judgement of base point parameters in the calculation of “rotation intersection” was solved effectively. And it provides a neat and practical method for the quick determination of the DOF and motion characteristics. Finally several typical examples from the literature were performed to show how to judge the validity of base point parameters and to calculate the DOF with the method mentioned above.

degree of freedom(DOF); fast solution; list intersection; virtual constraint

2013-11-08

国家自然科学基金资助项目(51005195, 51275438)；河北省高等学校科学技术研究项目(QN2014175)

TH112DOI：10.3969/j.issn.1004-132X.2015.04.018

卢文娟，女，1983年生。先进锻压成形技术与科学教育部重点实验室、燕山大学机械工程学院博士研究生。主要研究方向为并联机构自由度分析和型综合。发表论文10余篇。张立杰(通信作者)，男，1969年生。燕山大学机械工程学院教授、博士研究生导师。张一同，男，1945年生。燕山大学机械工程学院教授。