圆柱齿轮结构调频优化探索

徐永强，王蓉，张露军

（中国燃气涡轮研究院，成都610500）

圆柱齿轮结构调频优化探索

徐永强，王蓉，张露军

（中国燃气涡轮研究院，成都610500）

阐述了圆柱齿轮模态分析方法，联合UG和ANSYS软件建立了圆柱齿轮模态计算分析模型，并对圆柱齿轮结构调频优化进行了探索。结合不同结构齿轮模型的模态分析结果，通过对比分析归纳了其固有频率计算数据，得到相关规律，提出了齿轮结构调频优化方法。该方法减少了调频优化过程中不必要的迭代，提高了分析效率，为齿轮调频优化提供了理论依据和方法指导。

圆柱齿轮；模态分析；齿轮固有频率；有限元计算模型；结构优化；调频

1　引言

航空用齿轮工作转速高、载荷大，齿轮的节径型行波振动易导致齿轮故障［1］，造成不必要的损失，甚至出现人员伤亡。因此，齿轮设计时，除满足强度设计要求外，还需对其进行振动模态分析、结构调频优化，从结构设计上尽量避免发生共振［2-6］。

国外早期对齿轮动态特性的研究，一般是根据振动理论，采用集中参数法、有限元法及动态子结构模态综合法等进行齿轮的动态优化，并取得相应成果［7-8］。但直至目前，国外采用的分析方法依然很复杂，动态优化理论亦不完善。国内学者主要针对齿轮模态分析方法进行了研究，如李盛鹏等［2］在预应力作用下对齿轮模态进行了研究，王宇宁等［4］研究了热影响情况下齿轮的模态及共振可靠性，古莹奎等［5］在考虑接触情况下对齿轮进行了模态分析，但缺少对齿轮结构调频优化规律性探索。为此，本文针对圆柱齿轮振动模态进行计算，分析了结构调频优化过程，归纳总结出调频时圆柱齿轮结构变化对固有频率的影响，并得到相关规律。

2　有限元计算模型

计算选用的圆柱齿轮实体模型及简化后的模型结构见图1，各模型的具体结构尺寸参数见表1。表中b为齿宽，L为辐板厚度，D0为轮缘直径，D为分度圆直径，R1为辐板与轮缘过渡圆弧半径，R2为辐板与轮毂过渡圆弧半径。计算分析过程中，以模型1作为基准模型，其余模型作为对比模型，材料选用112Cr2Ni4A，参数按其工作温度150℃的各性能参数取值（弹性模量E=181.5 GPa，密度ρ=7 840 kg/m3，泊松比μ=0.3）。通过ANSYS软件建立有限元计算模型，选用单元类型为带中间节点的solid187，各模型分网后单元总数约为25万。计算模型中，配合轴承处轴颈上的所有节点施加径向约束，其中一端轴肩处的所有节点施加轴向约束，内花键分度圆面施加周向约束，搭建好的有限元计算模型见图2。

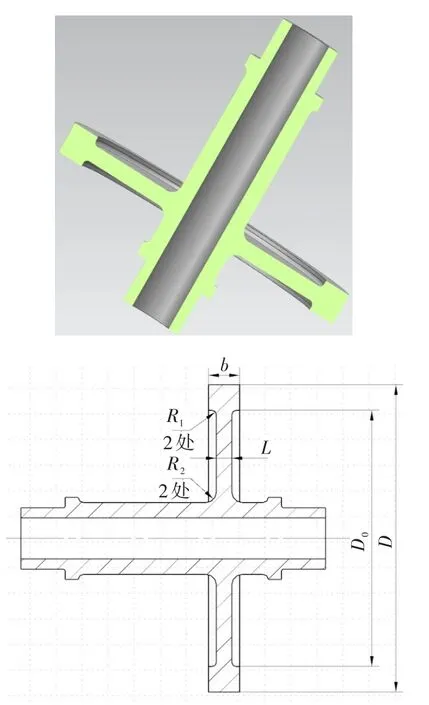
图1　圆柱齿轮实体模型及主要结构尺寸参数Fig.1 Solid model and structure parameters of cylindrical gear

表1　各计算模型的主要结构尺寸Table 1 The structure parameters of models

图2　圆柱齿轮有限元计算模型Fig.2 Finite element calculation model

3　计算结果与对比分析

3.1模型1计算结果

模型1模态计算结果只提取100～25 000 Hz的振动模态和对应频率，其余频率因超出分析频率范围而不再提取。其他计算模型做相同处理。

通过模态计算得到模型1示例齿轮的相关频率和振型。其各节径各阶次的固有频率见表2，一节圆及第1、2、3、4节径的振型见图3。模型2～11各节径振型图与模型1各节径振型图基本一致，后面不再给出。

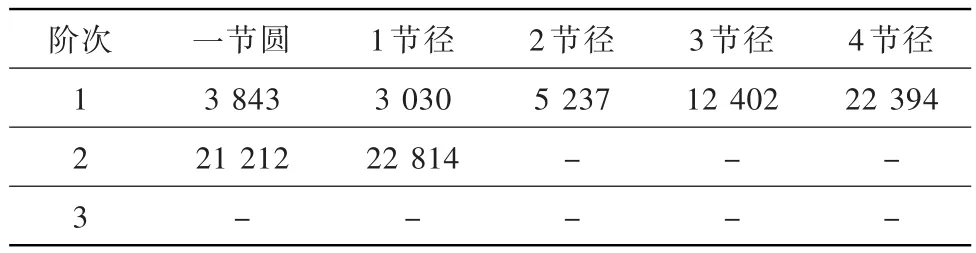
表2　模型1各节径各阶次的固有频率HzTable 2 Inherent frequency of each pitch diameter and each order of model 1

3.2轮缘与辐板过渡圆弧变化对结构调频优化的影响

3.2.1模型2计算结果及分析

在模型1基础上，模型2增大了R1，由0.8 mm调整为1.0 mm。其各节径各阶次固有频率见表3。

与模型1各节径各阶次频率对比分析可知：R1增大对高节径、高阶次固有频率略有影响，但不明显；同阶次下随着节径数的增加，固有频率增大，但增幅不显著；同节径下随着阶次数的增加，固有频率亦会增大，但增幅亦不明显。因此，增大R1对齿轮结构优化调频相对不敏感，尤其是对低阶次、低节径敏感度更低，甚至可忽略不计。

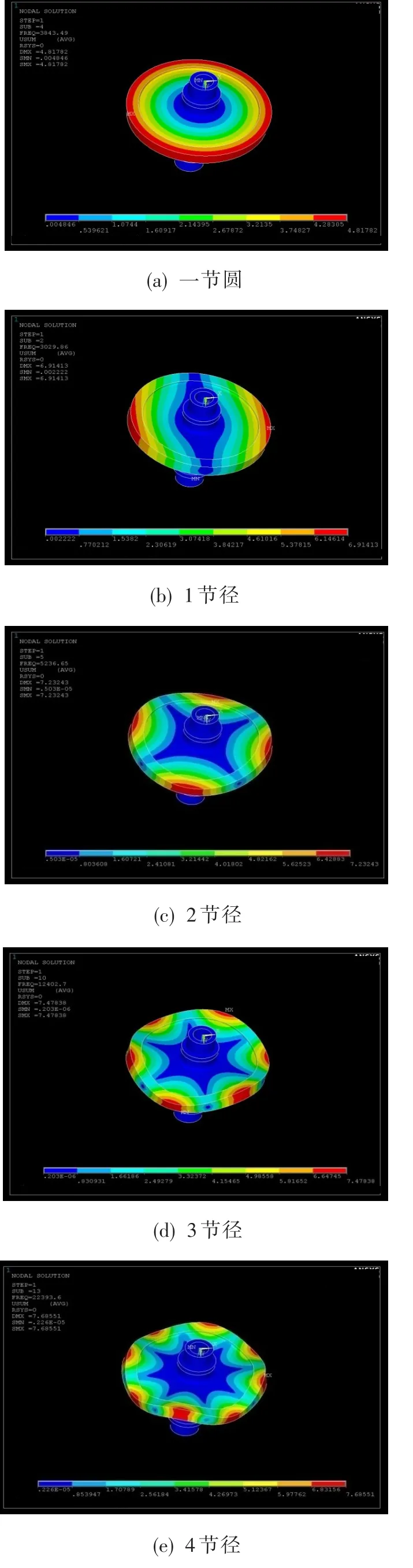
图3　模型1各节径的振型图Fig.3 Vibration mode of each pitch diameter of model 1

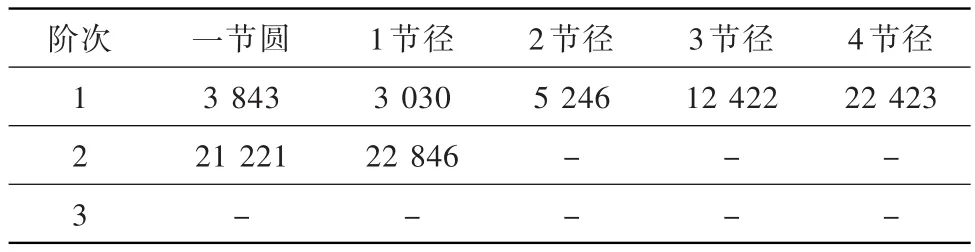
表3　模型2各节径各阶次的固有频率HzTable 3 Inherent frequency of each pitch diameter and each order of model 2

3.2.2模型3计算结果及分析

在模型1基础上，模型3减小了R1，由0.8 mm调整为0.6 mm。其各节径各阶次的固有频率见表4。

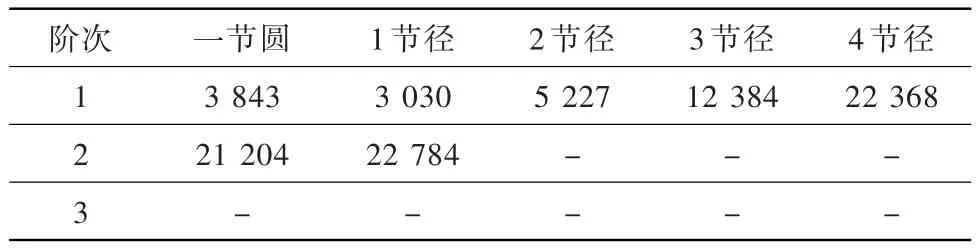
表4　模型3各节径各阶次的固有频率HzTable 4 Inherent frequency of each pitch diameter and each order of model 3

与模型1各节径各阶次频率对比分析可知：R1减小对高节径、高阶次固有频率略有影响，但不明显；同阶次下随着节径的增加，固有频率会适当减小，降幅不显著；同节径下随着阶次的增加，固有频率亦会适当减小，降幅亦不明显。因此，减小R1对齿轮结构优化调频相对不太敏感，对低阶次、低节径敏感度更低，甚至可忽略不计。

3.3辐板与轮毂过渡圆弧变化对结构调频优化的影响3.3.1模型4计算结果及分析

在模型1的基础上，模型4增大了R2，由2.0 mm调整为2.5 mm。其各节径各阶次的固有频率见表5。

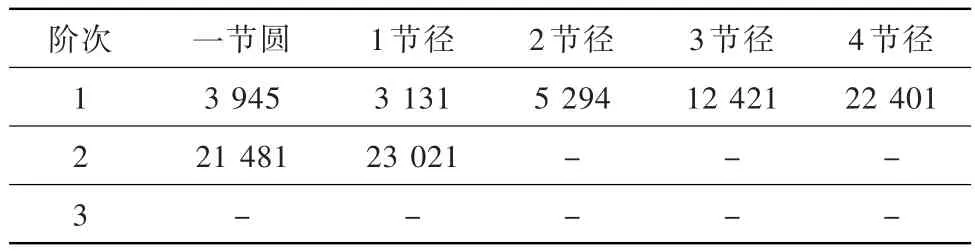
表5　模型4各节径各阶次的固有频率HzTable 5 Inherent frequency of each pitch diameter and each order of model 4

与模型1各节径各阶次频率对比分析可知：R2增大对低节径（一节圆、1节径）、高阶次固有频率影响大，固有频率都会较明显增加，且同节径下阶次越高频率增加越大；同阶次下随着节径的增加，2、3、4节径固有频率增加越来越小。

3.3.2模型5计算结果及分析

在模型1的基础上，模型5减小了R2，由2.0 mm调整为1.5 mm。其各节径各阶次的固有频率见表6。

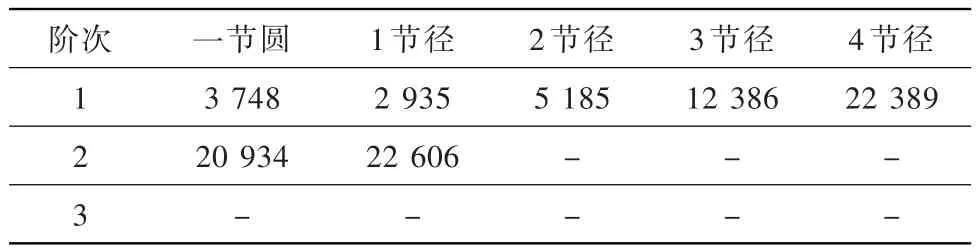
表6　模型5的各节径各阶次固有频率HzTable 6 Inherent frequency of each pitch diameter and each order of model 5

与模型1各节径各阶次频率对比可知：R2减小对低节径（一节圆、1节径）、高阶次固有频率影响大，固有频率都会较明显降低，且同节径下阶次越高频率减小越大；同阶次下随着节径的增加，2、3、4节径固有频率减小越来越小，到4节径时甚至可忽略不计。

3.4齿宽变化对结构调频优化的影响

3.4.1模型6计算结果及分析

在模型1的基础上，模型6减小了b，由6.0 mm调整为5.0 mm。其各节径各阶次的固有频率见表7。

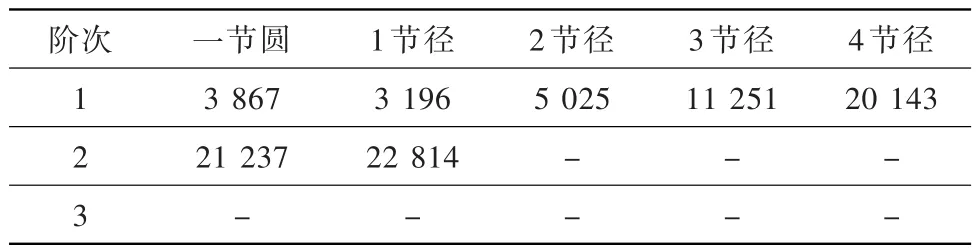
表7　模型6各节径各阶次的固有频率HzTable 7 Inherent frequency of each pitch diameter and each order of model 6

与模型1各节径各阶次频率对比分析可知：b减小后对低节径（一节圆、1节径）、高节径（2、3、4节径）固有频率影响趋势不同。一阶次下，一节圆到1节径，固有频率增加，且增频数值越来越大；高节径下，固有频率反而降低，且随着节径的增加降频数值逐渐加大。低节径下，固有频率增频数值会随着阶次的增加而减小，1节径下二阶次时已趋近于基准结构对应的固有频率值。

3.4.2模型7计算结果及分析

在模型1的基础上，模型7加大了b，由6.0 mm调整为7.0 mm。其各节径各阶次的固有频率见表8。

与模型1各节径各阶次频率对比分析可知：b增加对低节径、高节径固有频率影响趋势不同。一阶次下，一节圆固有频率略有增加，1节径固有频率减小，且随着阶次的增加低节径固有频率会逐渐增加；同阶次下高节径固有频率增加，且随着节径的增加增频数值逐渐加大。

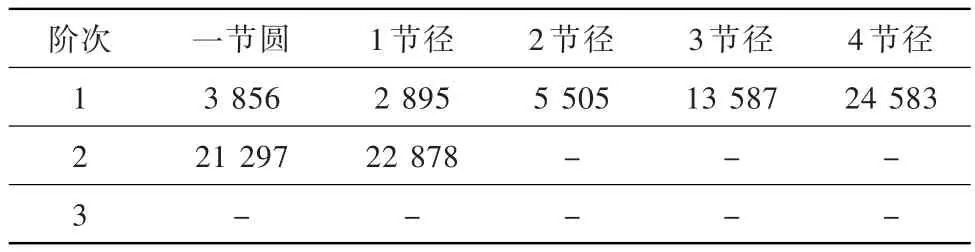
表8　模型7各节径各阶次的固有频率HzTable 8 Inherent frequency of each pitch diameter and each order of model 7

3.5辐板厚度变化对结构调频优化的影响

3.5.1模型8计算结果及分析

在模型1的基础上，模型8减小了L，由3.0 mm调整为2.5 mm。其各节径各阶次的固有频率见表9。

表9　模型8的各节径各阶次固有频率HzTable 9 Inherent frequency of each pitch diameter and each order of model 8

与模型1各节径各阶次频率对比分析可知：L减小对各节径、各阶次固有频率影响大，频率均会降低且降幅较大。同阶次下各节径降频数值基本一致，但由于同阶次下节径越高齿轮固有频率越大，所以同等降频数值下，对低节径的影响相对敏感度比对高节径的大。同节径时，阶次越高固有频率降低数值越大。

3.5.2模型9计算结果及分析

在模型1的基础上，模型9增加了L，由3.0 mm调整为3.5 mm。其各节径各阶次的固有频率见表10。

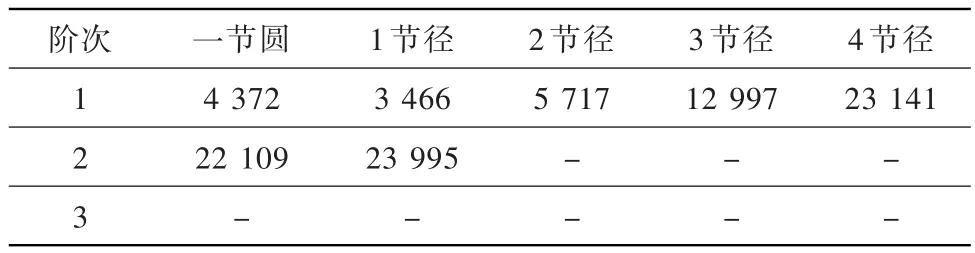
表10　模型9各节径各阶次的固有频率HzTable 10 Inherent frequency of each pitch diameter and each order of model 9

与模型1各节径各阶次频率对比分析可知：L增加对各节径、各阶次固有频率影响大，频率均会增加且增幅较大。同阶次下各节径增频数值基本一致，但由于同阶次下节径越高齿轮固有频率越大，所以同等增频数值下，对低节径的影响相对敏感度比对高节径的大。同节径时，阶次越高固有频率增加数值越大。

3.6轮缘直径变化对结构调频优化的影响

3.6.1模型10计算结果及分析

在模型1的基础上，模型10增大了D0，由50.0 mm调整为51.0 mm。其各节径各阶次的固有频率见表11。

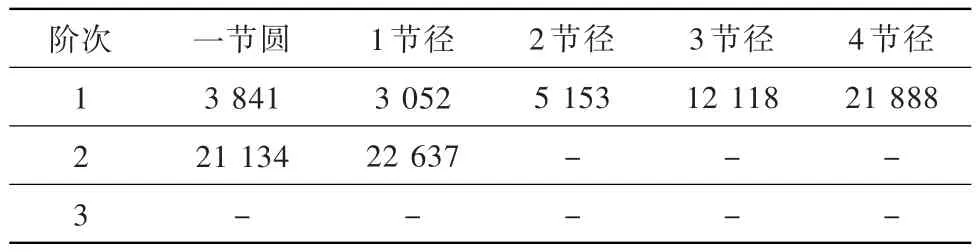
表11　模型10各节径各阶次的固有频率HzTable 11 Inherent frequency of each pitch diameter and each order of model 10

与模型1各节径各阶次频率对比分析可知：D0增大对一节圆1阶次固有频率基本无影响；1阶次时，1节径固有频率略有加大，而2、3、4节径固有频率逐渐降低，且随着节径的加大降频数值亦越来越大；2阶次时，固有频率会降低，且随着节径的加大降频数值也会越来越大。

3.6.2模型11计算结果及分析

在模型1的基础上，模型11减小了D0，由50.0 mm调整为49.0 mm。其各节径各阶次的固有频率见表12。

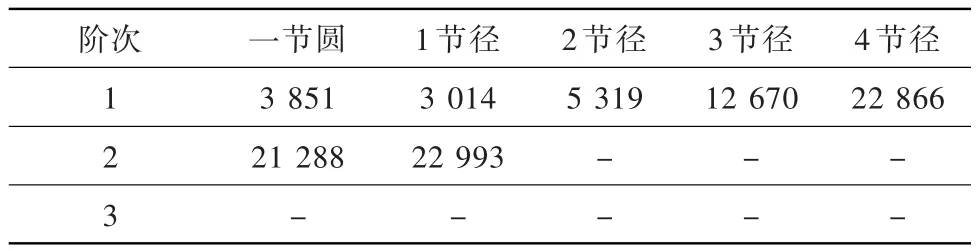
表12　模型11的各节径各阶次固有频率HzTable 12 Inherent frequency of each pitch diameter and each order of model 11

与模型1各节径各阶次频率对比分析可知：D0减小后，一节圆1阶次固有频率略微加大，基本可忽略不计；1阶次时，1节径固有频率略有减小，也基本可忽略不计，而2、3、4节径固有频率逐渐增加，且随着节径的加大增频数值亦越来越大；2阶次时，各节径固有频率会增大，且随着节径的加大增频数值也会越来越大。

4　结论

本文选取有代表性的圆柱齿轮结构模型作为研究对象，建立了11种结构调频实例模型，通过有限元计算对应结构的振动模态，并对提取的结果进行对比分析、归纳总结，得到了结构尺寸参数变化对圆柱齿轮频率的影响及优化调频的规律性和侧重性，可供圆柱齿轮结构调频优化借鉴和参考。具体为：

（1）辐板厚度、齿宽、轮缘直径、辐板与轮毂过渡圆弧半径的变化对固有频率影响较大，辐板与轮缘过渡圆弧半径变化对固有频率影响较小，调频时应优先考虑前者；

（2）辐板与轮缘过渡圆弧半径变化对固有频率影响较小，与其成正比关系，对低节径低阶次固有频率更不敏感，甚至可忽略；

（3）辐板与轮毂过渡圆弧半径变化对低节径、高阶次齿轮固有频率影响较大，固有频率与其成正比关系；

（4）齿宽变化对低阶次固有频率影响较为敏感，且低节径和高节径趋势不同，低节径下固有频率与齿宽成反比关系；

（5）辐板厚度变化对固有频率的影响较为敏感，固有频率与其成正比关系；

（6）轮缘直径变化对高节径高阶次固有频率的影响较为敏感，低节径低阶次下影响较小。

［1］《航空发动机设计手册》总编委会.航空发动机设计手册：第12册——传动与润滑系统［K］.北京：航空工业出版社，2002：602—611.

［2］李盛鹏，方宗德.预应力作用下弧齿内锥齿轮的动频率计算［J］.航空动力学报，2006，21（5）：949—955.

［3］郭伟超，王三民，付娜，等.某发动机齿轮转子的模态分析［J］.机床与液压，2006，（5）：57—59.

［4］王宇宁，孙志礼，杨强，等.基于热分析的齿轮模态及共振可靠性灵敏度研究［J］.东北大学学报，2013，34（3）：408—412.

［5］古莹奎，仝翔翔，储茜，等.全悬挂转炉倾动机构高速级齿轮模态分析［J］.机床与液压，2012，40（21）：157—159.

［6］吴文光，朱如鹏.基于Workbench的斜齿轮固有特性分析［J］.机械传动，2010，34（4）：54—55.

［7］Kahraman A，Singh R.Non-linear dynamics of a spur gear pair［J］.Journal of Sound and Vibration，1990，142（1）：49—75.

［8］Vaishya M，Houser R.Modeling and analysis of sliding friction in gear dynamics［C］//.Proceedings of the 2000 ASME Design Engineering Technical Conferences.Baltimore，USA：2000.

Research on structural frequency modulation optimization of cylindrical gear

XU Yong-qiang，WANG Rong，ZHANG Lu-jun
（China Gas Turbine Establishment，Chengdu 610500，China）

Cylindrical gear model analysis methods were introduced.The calculation analysis model of cylindrical gear was established by combining UG and the finite element ANSYS engineering application software，and the structural frequency modulation optimization was investigated.The calculating data of the inherent frequency was summarized using modal analysis results of different structure gear modals，and the correlation laws of frequency modulation were obtained.A method on structural frequency modulation optimization was put forward，which cut down unnecessary iteration during the optimization process to improve analysis efficiency so to provide theoretical basis and guideline for gear frequency modulation optimization.

cylindrical gear；mode analysis；gear inherent frequency；finite element calculation model；structural optimization；frequency modulation

V232.8

A

1672-2620（2015）06-0021-05

2015-05-05；

2015-11-28

徐永强（1984-），男，河南人，工程师，硕士，主要从事航空发动机传动系统设计与研究。