基于多重自相关算法的微弱正弦信号检测技术

范晓志

（北京工商大学材料与机械工程学院，北京　102488）

基于多重自相关算法的微弱正弦信号检测技术

范晓志

（北京工商大学材料与机械工程学院，北京102488）

离散小波变换具有时频分析特性，可把信号的细微变化反应出来，可明显提高信号的信噪比，在用小波变换进行预处理的前提下，利用正弦信号的特殊性质，在信号未知的情况下通过多重自相关运算可检测出埋没于噪声中的微弱正弦信号。讨论了多重自相关法在白噪声背景下、有色噪声背景下等情况的检测效果，并给出仿真结果。

离散小波变换；自相关；微弱信号；有色噪声

0　引言

目前的许多研究和应用领域中，都涉及到微弱信号的精密测量。然而对任何一个系统，必然存在噪声，当所测量的信号又相当微弱时，如何把淹没于噪声中的有用信号提取出来的问题越来越引起人们的关注。微弱信号的检测方法很多，而对于微弱信号的时域处理，自从60年代的Boxcar积分器以来，一直没有特别有效的改进方法［1，2］，为此提出一种基于小波变换和多重自相关的时域检测方法，此方法可在正弦信号频率未知的条件下有效提高对信号的检测能力。

1　用小波变换提升信号的信噪比

小波分析是一种信号的时间尺度（时间-频率）的分析方法，具有多分辨率分析的特点，而且在时频两域都具有表征信号局部特征的能力，是一种窗口大小固定但形状可变，时间窗和频率窗都可以改变的时频局部变化分析方法。即在信号低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率。利用小波的这些优点，可以对获取的微弱的信号进行预处理，在强背景噪声下显现并增强信号的目标特性，提高信噪比。外界噪声一般可以等效的看作是宽带平稳加性高斯白噪声，且n（t）～N（0，σ2）信号和噪声在小波变换后有着不同的特性，利用此方法进行微弱信号检测的技术见文献［3］。但当信号非常微弱时，信号经小波分析处理后，有可能被测信号功率仍然小于噪声功率，甚至有可能仍然相当微弱，比噪声小几个数量级甚至被噪声淹没时，或者在某些特定场合下噪声不理想，不能在看成白噪声时，利用小波变换就有局限性了。在这种情况下，我们可以利用信号和噪声在时间特性上的差别，利用信号和噪声两种函数在统计特性上的可区分性，利用信号在时间上相关的特性，把埋没于噪声中的周期信号提取出来，这就是信号的相关检测。

2　多重自相关法

传统的自相关检测法，是将输入信号和延迟τ后的输入信号通过自相关运算，利用信号和噪声、噪声和噪声的不相关特性达到提高信噪比的目的［5，6］。设输入信号为：

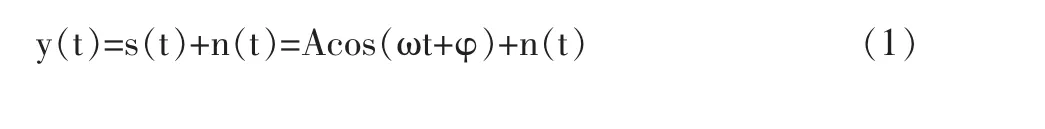
其自相关函数为：对于具备各态历经性的过程，可利用样本函数的时间自相关函数来代替随机过程的自相关函数。此时，自相关函数可以表示为：

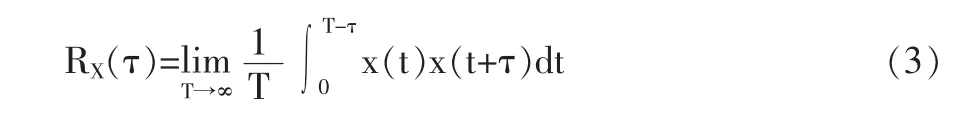
考虑到实际测量中观测时间T总是有限的，故通常按下式实现相关运算：

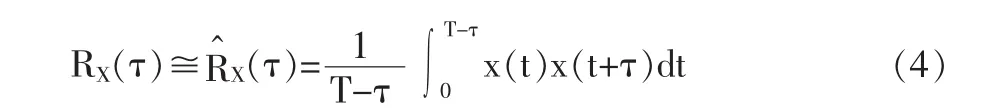
（1）信号的自相关函数：

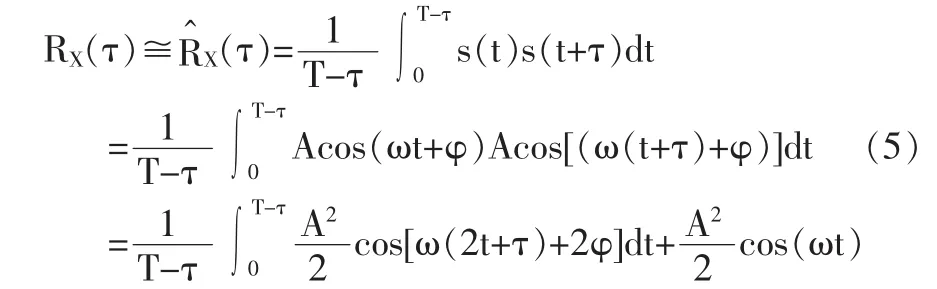
（2）信号与噪声的互相关函数。若噪声为标准的高斯白噪声，则E［n（t）］、E［n（t+τ）］均为0，从而E［s（t）n（t+τ）］、E［s（t+τ）n（t）］也都为0。但实际测量中，观测时间是有限的，噪声白化程度不一定十分理想，从而导致E［n（t）］、E［n（t+τ）］不一定为0，因此根据式（4）信号与噪声的相关函数可以表示为：

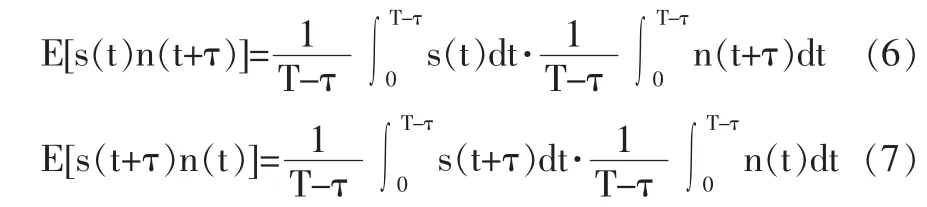
（3）噪声的自相关函数。在理论上高斯白噪声除τ=0外其余值均为0，但实际情况不能达到理论设想，因此RN（τ）（τ≠0）总是存在的，且是τ的函数［4］，但其幅度与原噪声相比很小，可看作新的噪声，至于RN（τ）是一个比较大的数，在实测或仿真时可以不计算，用0代替。基于以上讨论，可将式（2）写为：

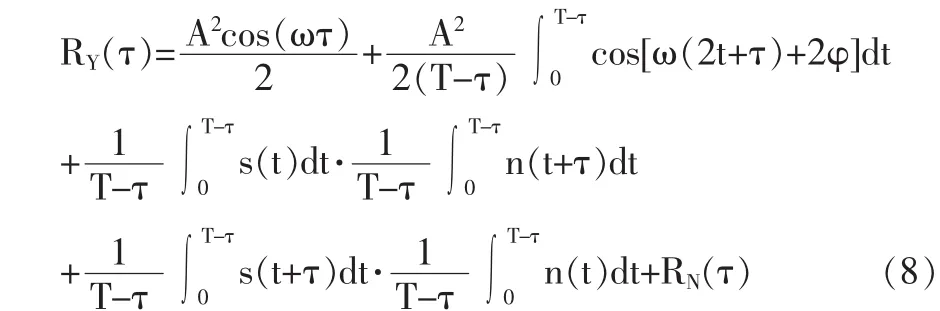
式（8）很复杂，很难化简，若将积分时间由T-τ改为T，则上式可化简为：

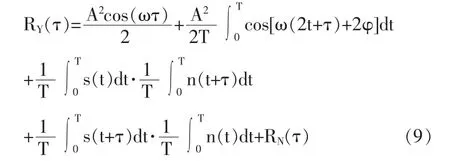
式（1）可改写为：

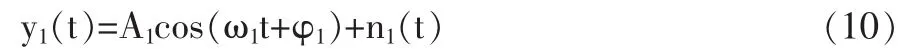
式中A1cos（ω1t+φ1）是RS（τ）和E［s（t+τ）n（t）］的叠加；n1（t）是E［s（t）n（t+τ）］和RN（τ）的叠加。对比式（1）和（10），尽管两者信号的幅度和相位不同，频率却没有变化，它通过相关运算增加了信噪比，但改善程度有限，多重自相关法是将当作重复上述步骤多次，自相关次数越多，信噪比提高的就越多，因此可检测出淹没于噪声中的微弱信号。值得注意的是，为使式（8）的计算简化，将积分时间增加到T，从而必须得到T-τ之外的s（t+τ）和n（t+τ）的信息，对于循环卷积，不考虑噪声，若采样周期为信号频率的整数倍可用前部分信息充当s（t+τ）从T-τ到T的信息，如图1所示；若采样周期不是信号频率的整数倍，仍采用这种信息替代，则可能得到图2所示的自相关图形信号的幅度变化很大，无法继续计算。为此，可采用相关积分的方法，即把采样时间变为2T，然后对0-T积分，从而有效的解决了这一问题。

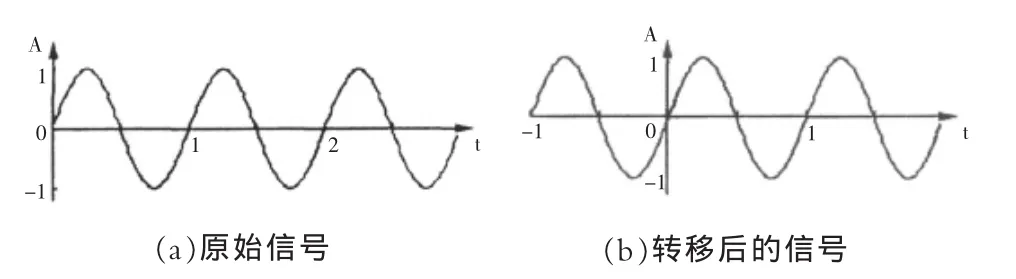
图1　原始信号和转移后的信号

图2　自相关图形

图3　淹没于噪声中的输入信号

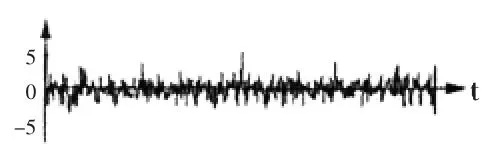
图4　一次相关运算后的结果

图5　四次相关运算后的结果

3　多重自相关法的应用

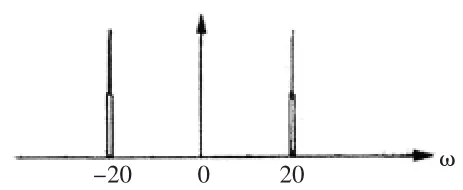
图6　四次相关后的频谱

（2）多重自相关法在有色噪声中的应用。在某些特定情况下，混于信号中的噪声不是4结论

很理想时，就不能再把噪声看成白噪声了。对有色噪声，其自相关函数不再是冲击函数，且在一定范围内相关性有可能很强，但在这一范围之外，其相关函数仍然是趋于0的，其幅度小于原始信号的幅度，我们可以只截取相关性较弱的一部分，将其送入相关器，多次运算即可得到原始信号的频率。如图（4）为含噪正弦信号的（信噪比为-20dB）功率谱密度图形经4次相关运算后的功率谱密度。可以证明，多重自相关法还可以推广到同时对多个正弦信号的检测中去［7］。

针对微弱正弦信号的检测，在应用小波变换进行预处理的前提下，提出多重自相关检测微弱正弦信号的方法，通过仿真证实了这种方法的有效性，这种方法在频率测量中具有极高的准确性；在幅度测量上，通过多次测量取平均值，也可达到预期的精度。与传统的微弱信号时域处理方法比较，多重自相关检测方法理论推导简单，意义明确，另外，这种方法对噪声白化要求低，便于工程应用。

［1］MALLATS，ZHONG Si-fen.Characterization of signals from multiscale edges［J］.IEEE Transactions on pattern analysis and machine intelligence，1992，7.

［2］周浩敏，韩颖.硅微传感器中微弱信号的相关检测［J］.北京航空航天大学学报，1999，1.

［3］范晓志.小波变换的信号去噪应用［J］.武汉科技大学学报，2004，3.

［4］NEWLAND D E.Harmonic wavelets in vibrations and acoustics［J］. Royal Soc Trans Philos:A 1999.

［5］SHERLOCK B G，KAKAD Y P.Windowed discrete cosine and sine transforms for shifting data［J］.Signal processing，2001，7.

［6］NEWLAND D E.Ridge and phase indentification in the frequency analysis of transient signals by harmonic wavelets［J］.J of Vibration and Acoustics，Transactions of the AS ME，1999，2.

［7］胡莺庆.随机共振原理在强噪声背景信号检测中的应用［J］.国防科技大学学报，2001，4.

［8］张志涌，等.MATLAB教程-基于6.x版本［M］.北京航空航天大学出版社，2003.

An Inspecting Technology for Weak Sinusoidal Signal Based on Wavelet Analysis and Multi-layer Autocorrelation

FAN Xiao-Zhi
（School of Material and Mechanical Engineering，Beijing Technology and Business University，Beijing 102488，China）

Discrete wavelet transform（DWT）is a time-frequency analysis technology，which detects the subtle small changes in the signal spectrum and can improve the SNR.Based on the DWT，considering the sinusoidal signal has a particular autocorrelation trait，it is possible to detect the unknown weak signal in power noise.Multiple statuses are studied，when sine signal are disturbed by white noise or colored noise.Finally，the paper offers a simulation results.

discrete wavelet transform；auto correlation；weak signal；colored noise

TN911

A

10.3969/j.issn.1002-6673.2015.06.038

1002-6673（2015）06-107-03

2015-09-07

范晓志（1971-），男，硕士，讲师。研究方向：智能信息处理，发表论文十多篇。