两电机变频系统神经网络逆PID的控制

张锦，高磊，仲伟松

（宿迁学院，江苏宿迁　223800）

两电机变频系统神经网络逆PID的控制

张锦，高磊，仲伟松

（宿迁学院，江苏宿迁223800）

由于两电机变频系统非线性强耦合性，先搭建由神经网络辨识原系统的广义逆模型，再与原系统串联，从而构成复合伪线性系统，使系统解耦线性化。然后引入PID控制以提高系统的鲁棒稳定性。实验结果表明，此方法不仅较好地实现了系统的解耦，而且鲁棒稳定性较强。

神经网络逆；两电机变频系统；解耦

0　引言

多电机同步控制系统在现代工业生产中应用广泛，高性能的多电机同步调速系统可有效提高产品品质及经济效益。目前我国以速度与张力为控制对象的同步调速系统多为直流传动方式，直流传动控制简单，调速性能良好，但存在制造及维护成本高，容量小等缺陷。随着电力电子技术及计算机控制技术的高速发展，多台交流电机同步控制性能逐渐提高，其结构简单且制造及维修成本低，但这类控制的高阶、非线性、强耦合问题如何解决是当前研究的瓶颈［1］。

逆系统的出现为解决这类控制问题提供一条有效途径。但该方法要求模型精确可知，按照传统逆系统方法得到这类非线性系统的数学模型较困难。因此有学者提出基于神经网络［2］构建逆系统的方法来解决此问题。神经网络具有自学习、自适应等功能，可以做到不依赖被控对象的数学模型，具有较强的适应能力和实时性，用这种方法可以有效解决逆系统模型中建模困难等问题。因此使用神经网络辨识由多电机变频系统构成的原系统，串联于原系统前，从而构成复合伪线性系统，完成了系统的解耦与线性化。由于在构建过程中难免会出现一些建模误差，所以选择PID控制器［3］以确保系统的鲁棒性。

本文以两电机变频调速系统为研究对象，将广义逆辨识两电机控制系统方法与PID控制相结合，并以多电机变频系统实验平台进行实验研究。

1　两电机变频系统数学模型

图1为两电机变频同步调速系统转速与张力控制结构示意图。

图1　两电机变频系统结构示意图Fig.1 Control diagram of two-motor variable frequency system

基于矢量控制方式下且磁通稳定时，其数学模型可简化为［4］：

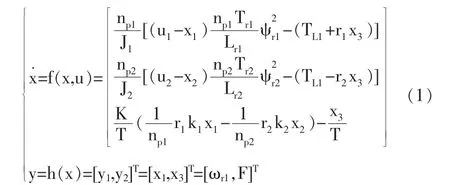
式中：下标1、2分别表示第1、2台电机。k，r分别为皮带轮的速比、半径；J—转子转动惯量；ω—定子频率的同步角速度；TL—负载转矩；Tr—电磁时间常数；ψr—为转子磁链；Lr—转子自感；ωr—电气角速度；K—传递函数；T—张力变化常数；np—电机的极对数；F—皮带的张力。其中状态变量控制变量为

2　系统广义逆的实现

将式（1）中输出求导，得其Jacobi矩阵为：

根据广义逆理论［5］，系统的向量本阶性为3，而系统的相对阶为a=（1，2），即阶数为a1+a2=3，因此系统的本阶性等于向量相对阶，可知此系统可逆。由此系统的广义逆可表示为：

其中：a10=1，a11=1；a20=1，a21=1.414，a22=1。将广义逆系统与两电机变频系统串接，即构成广义伪线性复合系统，其输入输出传递函数为：

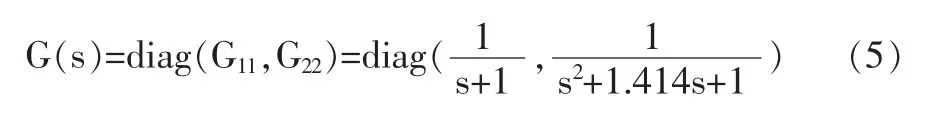
3　神经网络广义逆PID控制策略

首先构建由神经网络辨识的原系统（两电机变频系统）广义逆模型：①向原系统给定足够的激励信号；②取原系统的输出作为神经网络逆系统的输入，而原系统输入作为神经网络逆系统的输出，并对采样信号进行归一化处理；③神经网络的结构采用5-10-2的3层BP网络。中间层传函采用tansig，输出层传函采用purelin，学习函数采用梯度递减训练函数traingdx，判断误差收敛趋势是否符合要求。

将由神经网络逼近的广义逆模型与以两电机同步系统为构成的原系统串接，从而行成复合伪线性系统。由式（5）可知，原系统转化为1/（s+1）的速度子系统及1/（s2+ 1.414s+1）的张力子系统。

转化后的伪线性系统实现了原系统的解耦与线性化，但由于存在开环建模误差，此时引入PID控制从而取得更好的闭环控制效果。确定最佳PID参数后，从而构成了神经网络逆PID闭环控制系统。如图2所示。

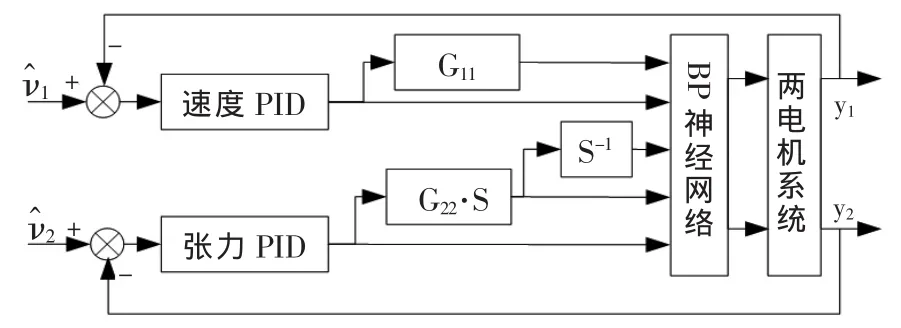
图2　神经网络逆PID控制原理图Fig.2 Diagram of NNGI-PID control system

4　实验研究

图3所示为多电机变频系统试验平台。本文以其中2台电机为研究对象。试验平台包括上位机监控软件WinCC，S7-300PLC及SM335高速模拟量输入模块，FM350高速计数器模块，SL100型张力传感器，及光电编码器，2台MMV变频器，2台2.2 kW的三相异步电机。

图3　多电机变频系统试验平台Fig.3 Experiment platform of multi-motor variable frequency systems

为了使原系统稳定先设计PID控制器，接着速度给定为200～600 r/min的随机方波，张力给定为200～600 N的随机方波，然后在PLC中构建神经网络以逼近原系统的广义逆，组成神经网络广义逆系统，最后引入PID算法以消除建模及稳态误差。

试验结果如图4～5所示。传统PID控制，速度在突变时，张力存在较大波动。而采用神经网络广义逆PID控制时，张力受速度突变影响较小，较好地实现了张力与速度的解耦。

5　结束语

图4传统PID控制时系统实测响应波形
Fig.4 Measured responses with conventional PID control

由神经网络构建的广义逆模型与PID相结合的控制方法。经过多电机变频系统试验平台研究，可得出如下结论：

（1）由感应电机组成的两电机变频系统速度与张力的耦合性很强，传统PID可一定程度上缓解系统耦合问题，但耦合度依然很大。

（2）对比传统PID方法，神经网络逆PID控制具有更好的鲁棒稳定性。

图5　神经网络广义逆PID控制时系统实测响应波形Fig.5 Measured responses with NNGI-PID

［1］李春文，冯员锟.多变量非线性控制的逆系统方法［M］.北京：清华大学出版社，1991.

［2］朱大奇.人工神经网络研究现状及其展望［J］.江南大学学报，2004，1.

［3］王伟，张晶涛，柴天佑.PID参数先进整定方法综述［J］.自动化学报，2000，3.

［4］张懿，刘国海，魏海峰，等.基于最小二乘支持向量机左逆的两电机变频调速系统张力辨识策略［J］.中国电机工程学报，2010，30.

［5］刘国海，张锦，赵文祥，等.两电机变频系统的支持向量机广义逆

Neural Network Generalized Inverse Based on Two-motor Variable Frequency System PID Applications

ZHANG Jin，GAO Lei，ZHONG Wei-Song
（School of Suqian College，Suqian Jiangsu 223800，China）

Due to the nonlinear heavy-coupling characteristic in two-motor variable frequency systems，the generalized inverse model of original system is approximated by neural network firstly，then the pseudo-linear system is formulated by integrating the original system with this model，and the system's decoupling linearization are achieved.Then the robustness can be improved by means of the PID controllers. The experimental results show that the control strategy has good decoupling performance and can deal with external disturbances with strong robustness.

neural network generalized inverse（NNGI）；two motor variable frequency systems；decoupling

TH-39

A

10.3969/j.issn.1002-6673.2015.06.045

1002-6673（2015）06-126-03

2015-09-28

宿迁学院科研基金项目（2014KY09）；江苏省自然科学基金项目（BK20140586）

张锦（1986-），男，硕士研究生，助教。从事电机控制技术方面研究。