基于GARCH类模型的煤矿安全事件舆情波动性研究*

张 华杨 雪李松华王 菲

（1.中国矿业大学（北京），北京市海淀区，100083；2.华北水利水电大学，河南省郑州市，450045）

基于GARCH类模型的煤矿安全事件舆情波动性研究*

张 华1杨 雪2李松华2王 菲2

（1.中国矿业大学（北京），北京市海淀区，100083；2.华北水利水电大学，河南省郑州市，450045）

运用GARCH类计量经济学模型，分析了煤矿安全事件舆情演化的波动性特征，基于2011年1月1日-2014年5月16日的煤矿事故百度搜索指数的周平均数据的实证研究发现：煤矿安全事件舆情演化的波动性呈现出聚集效应；通过对模型残差进行条件异方差即ARCH效应检验，发现煤矿事故搜索指数的波动性具有ARCH效应，因此，对煤矿安全事件舆情演化波动性的研究适用GARCH类模型，模型结果可以为煤矿安全事件舆情的预警提供先决信息。

GARCH模型 煤矿安全 舆情 波动性

煤矿安全事件舆情，即公众对煤矿事故的关注，其演化波动呈现出由初步传播到迅速扩散再到消减的生命周期性特征。同时，煤矿安全舆情的波动具有聚集性和非对称性特性，对于这些特性的把握，一般的时间序列建模的ARMA模型显得无能为力。因此，对于煤矿安全事件舆情波动性的研究，可以采用金融时间序列波动性应用较多的GARCH类模型。

1　变量选取和平稳性检验

1.1变量选取和统计描述

煤矿安全事件爆发后舆情演变的表征性指标包括电视、报纸以及网络等媒体报道关注情况，基于数据的可得性，本项研究选择了煤矿事故搜索百度指数作为煤矿安全事件舆情的替代指标，以SIt表示，样本长度为2011年1月1日-2014年5月16日，数据频率为周平均数据。舆情演化具有由初步传播（即形成）到迅速扩散（即发展）再到消退的周期性特征，煤矿安全事件的舆情也不例外、具有这一周期性特征，如图1所示。

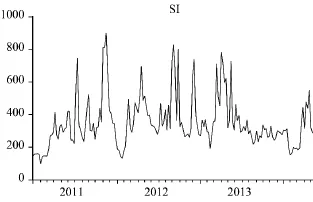
图1　2011年1月1日-2014年5月16日煤矿事故搜索指数情况

此外，突发事件舆情演化呈现出波动聚集性特征，即一段时间内波动性较大，而在另一段时间内波动性较小。原因在于突发事件发生后，公众由于从众心理关注事件从而导致网络点击和搜索迅速增加，而关注度的上升有可能意味着新一轮的舆论波动。图1为煤矿事故搜索指数体现出煤矿安全事件舆情演化的聚集性特征，图2为煤矿事故搜索指数变化率情况，它明确显示了该聚集性特征。定义煤矿事故搜索指数变化率RSIt=ln（SIt/SIt-1）。

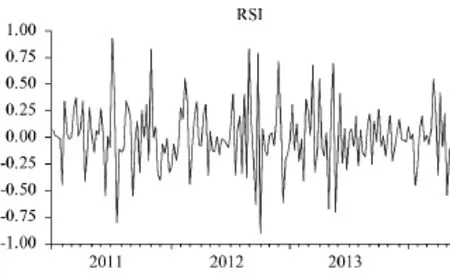
图2　2011年1月1日-2014年5月16日煤矿事故搜索指数变化率情况

1.2变量平稳性ADF检验

为避免采用时间序列数据进行实证研究可能出现的 “伪回归”现象，即回归残差非平稳、回归关系不能真实反映被解释变量和解释变量之间的均衡关系，需要对煤矿事故搜索指数序列进行平稳性检验。本部分采用应用较为广泛的ADF方法来检验序列的平稳性，检验结果如表1所示。由表1可知，煤矿事故搜索指数序列SIt的ADF检验值为-6.236，小于1%显著性水平下的临界值，接受序列存在单位根原假设的概率p值为0.000，根据小概率事件不易发生的原则，拒绝序列存在单位根的原假设，因此，煤矿事故搜索指数序列SIt为平稳序列。

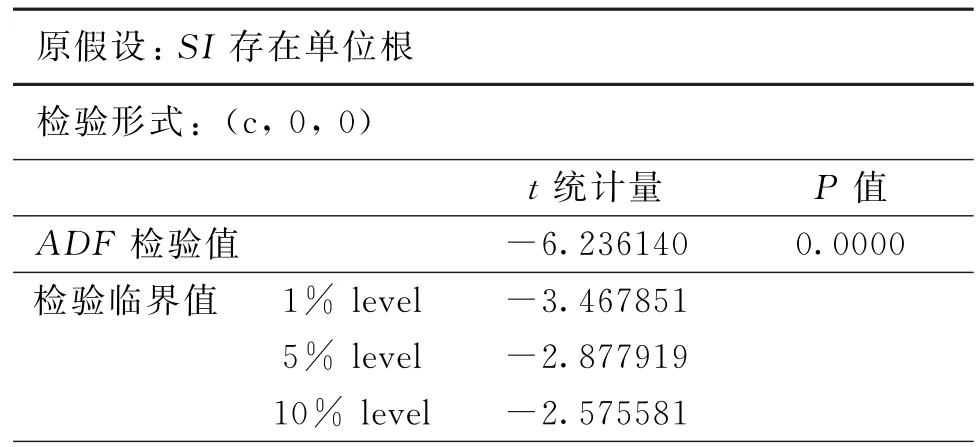
表1　序列平稳性ADF检验

2　煤矿事故舆情波动的ARCH效应检验

2.1自回归阶数选择

舆情演化的生命周期呈现出自回归特性。本部分采用偏自相关系数PAC来确定自回归条件异方差ARCH模型中条件均值方程的形式，即自回归的阶数。图3的煤矿事故搜索指数SIt序列的偏自相关系数PAC的检验结果显示，条件均值方程的自回归阶数选择为1，原因是偏自相关系数PAC在滞后1阶时截尾。

煤矿事故舆情演化的一阶自回归过程可由最小二乘回归得到:

方程（1）式中圆括号中的数字为对应参数的t检验值，说明各回归系数是显著的。

2.2ARCH效应检验

由自回归方程（1）的残差图4可以看出，残差的波动呈现聚集性，说明误差项可能存在条件异方差。

对于回归方程误差项即残差项的条件异方差特性即ARCH效应检验，通常采用Engle（1982）提出的拉格朗日乘数检验，即ARCH LM检验。该检验通过如下辅助回归进行:

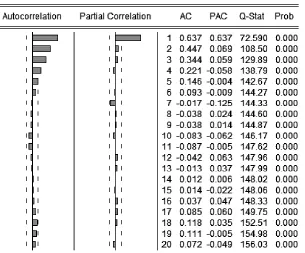
图3　ARCH模型均值方程自回归阶数选择

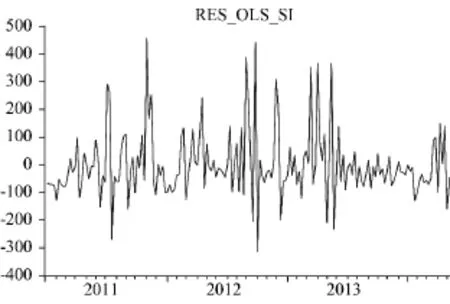
图4　煤矿事故搜索指数自回归方程的残差

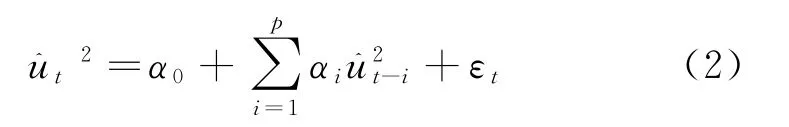
ARCH LM检验基于（2）式回归的拟合优度R2构建服从χ2（p）分布的拉格朗日统计量LM=TR2来检验残差序列是否存在ARCH效应，其中T为样本观测个数。若LM＞χ2（p）则拒绝原假设αi=0（i=1，…p）而接受αi不全为0的备选假设，即残差序列存在ARCH效应。

表2给出了回归方程（1）式残差序列条件异方差的ARCH LM检验结果，其中ARCH项滞后阶数的选择为1。由表2可知，ARCH LM统计量的值为8.4807，接受不存在条件异方差原假设的概率p值为0.0036、小于显著性水平1%，因此，拒绝原假设，从而可以认为煤矿事故搜索指数SIt自回归方程（1）式的残差存在条件异方差性即ARCH效应，可以用GARCH类模型来分析煤矿安全事件舆情的波动性。其中，ARCH LM检验中的辅助回归方程估计如下:

表2　煤矿事故舆情波动的ARCH LM检验

2.3GARCH效应检验

由上文煤矿事故搜索指数SIt及其自回归残差序列呈现聚集性，以及煤矿事故搜索指数自回归残差的ARCH效应检验可知，煤矿安全事件舆情演化即煤矿事故搜索指数的残差序列存在条件异方差，则为了更好地描述煤矿安全事件舆情演化的波动性特征，本部分采用GARCH模型来建模分析。其中，GARCH（q，p）模型中的均值方程仍采取随机游走的自回归形式，条件方差方程中的ARCH项和GARCH项阶数的选择则通过不同模型的比较而得以确定。GARCH（q，p）模型的具体形式如下:

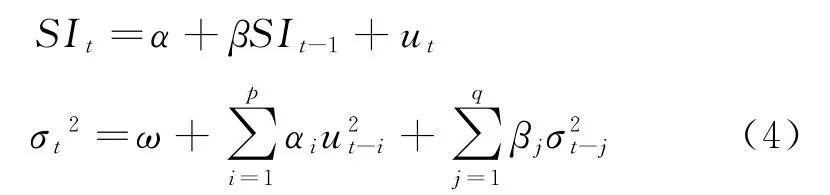
（4）式中第一个方程即为均值方程、第二个方程为条件方差方程。为确定条件方差方程中ARCH项和GARCH项的阶数，选择了GARCH（1，1）、GARCH（1，2）、GARCH（2，1）以及GARCH（2，2）4个模型进行比较，如表3所示。

表3　煤矿事故舆情波动的GARCH模型选择

最优GARCH模型的选择规则是模型的对数似然值较大而赤池和施瓦茨信息准则较小，同时参数的估计值显著，则由表3的结果可知，最优模型应为GARCH（1，1），其估计结果如下:

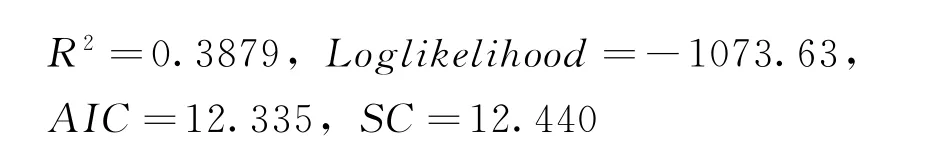
（5）式GARCH（1，1）模型中的均值方程与上文（1）式的煤矿事故舆情演化的一阶自回归随机游走模型相比，具有较大的对数似然值和较小的AIC和SC值，同时GARCH（1，1）模型中条件方差方程的3个参数均为正、统计上均显著、模型估计合理，从而说明模型GARCH（1，1）较优，能够更好地模拟煤矿事故搜索指数的波动性特征，如图5所示。由图5可以看出，GARCH（1，1）模型不仅成功地模拟了煤矿事故搜索指数的每一次突变，而且对煤矿事故搜索指数突变强度的把握也较为理想，因此，GARCH（1，1）模型较为成功地刻画了煤矿安全事件舆情演化的波动性特征，可以为煤矿安全事件舆情的预警提供先决信息。

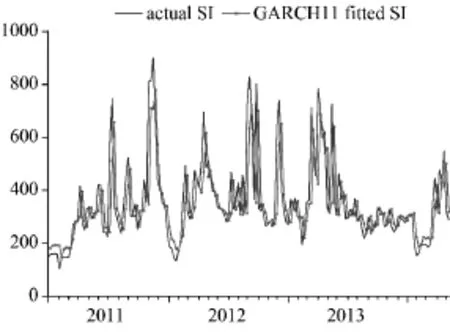
图5　GARCH（1，1）模型对煤矿安全事件舆情波动性的模拟

此外，GARCH（1，1）模型克服了煤矿事故搜索指数自回归残差序列所存在的条件异方差性，如表4所示:GARCH（1，1）模型残差序列异方差的ARCH LM检验统计量接受原假设即不存在条件异方差的概率为0.8286，置信度较高，且相伴概率也高达0.8299，由此说明GARCH（1，1）模型克服了煤矿事故舆情演变方程残差序列所存在的ARCH效应，图6的自相关、偏自相关检验结果也支持了这一结论:自相关系数AC和偏自相关系数PAC的值都近似为0，Q统计量不显著的概率在0.827以上。

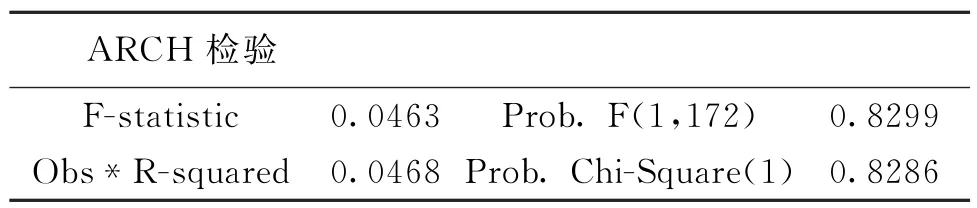
表4　煤矿事故舆情波动GARCH（1，1）模型的ARCH LM检验

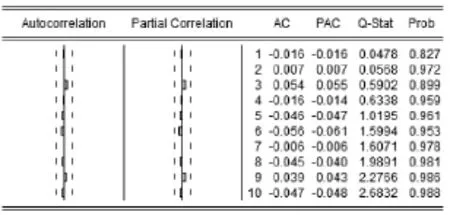
图6　GARCH（1，1）模型残差平方相关图

3　煤矿事故舆情波动的非对称效应检验

在资本市场上，金融资产价格的变化往往表现出这样一种现象:金融资产价格的波动对市场上的好消息和坏消息的反应不同——坏消息对金融资产价格波动性的影响要大于好消息的，即存在着非对称性效应，亦即杠杆效应。这一现象在舆情演化的波动性中也存在，如万源（2012）认为网络舆情信息演化的波动性即存在这种非对称性效应。因此，为了检验煤矿安全事件舆情演化的波动性是否存在非对称性效应，本节将应用门限ARCH模型即TARCH模型进行检验。

3.1TARCH模型估计

一般地，TARCH模型中的条件方差方程形式如下:

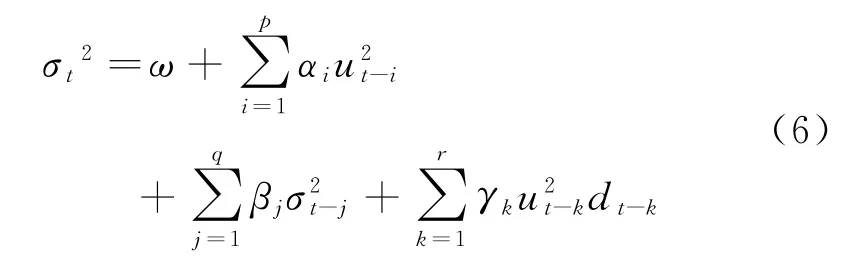
其中，dt-k为虚拟变量，当ut-k＜0（即坏消息）时，dt-k=1；相反，当ut-k＞0（即好消息），则dt-k=0。如果γk≠0，则非对称效应存在，且如果γk＜0，则说明非对称效应使波动变小；反之，如果γk＞0，则说明说明非对称效应使波动变大。

表5给出了门限阈值分别取1和2的TARCH模型估计结果的相关指标，由各指标的比较可知，TARCH（1，1）模型的性能相对较好。同时，门限阈值取1和2时，对条件方差方程中的ARCH项和GARCH项阶数分别取高阶，TARCH模型估计结果的性能也不比TARCH（1，1）模型要好，因此，对于煤矿安全事件舆情演化波动性的非对称效应的检验采取了TARCH（1，1）模型。

TARCH（1，1）模型的估计结果如（7）式:

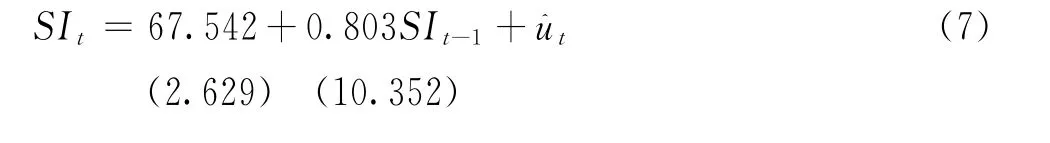
表5　煤矿事故舆情波动非对称性效应检验的TARCH模型选择

（7）式中，非对称效应项的系数估计值为-0.393，统计上显著不为0，从而说明煤矿事故搜索指数的波动性存在非对称效应。对于煤矿事故，消息性质的界定与一般资本市场消息的界定不同，因为煤矿事故发生本身就是坏消息，必然会引致公众的关注和舆情上升，反映为煤矿事故搜索指数上升。因此，在煤矿事故搜索指数波动性TARCH建模中，好消息界定为ut-1＜0（因为好消息使舆情关注下降），此时虚拟变量dt-1应取值为1；相反，坏消息时即ut-1＞0，dt-1取值为0。由（7）式的TARCH模型估计结果可知，好消息对煤矿事故搜索指数波动性的冲击为0.015倍，而坏消息对煤矿事故搜索指数波动性的冲击为0.408倍。

3.2TARCH模型效果分析

由图7的TARCH模型和GARCH模型对煤矿事故搜索指数波动性的模拟比较可知，TARCH模型比GARCH模型的表现更优，TARCH模型无论是对煤矿事故搜索指数波动性的形态还是程度的模拟都要好于GARCH模型。

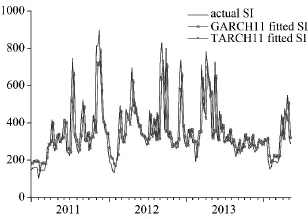
图7　TARCH、GARCH模型对煤矿安全事件舆情波动性的模拟与比较

同样地，TARCH（1，1）模型也克服了煤矿事故搜索指数自回归残差序列所存在的条件异方差性，如表6所示:TARCH（1，1）模型残差序列条件异方差的ARCH LM检验统计量接受原假设即不存在条件异方差的概率为0.5827，置信度较高，且相伴概率也高达0.5853，由此说明TARCH（1，1）模型克服了煤矿事故舆情演变方程残差序列所存在的ARCH效应。自相关、偏自相关检验结果也支持了这一结论:自相关系数AC和偏自相关系数PAC的值都近似为0，Q统计量不显著的概率基本都在0.857以上。

表6　煤矿事故舆情波动TARCH（1，1）模型的ARCH LM检验

4　结语

本研究运用GARCH类计量经济学模型分析了煤矿安全事件舆情演化的波动性特征，基于2011年1月1日-2014年5月16日的煤矿事故百度搜索指数的周平均数据的实证研究发现:

（1）基于对煤矿事故搜索指数及其变化率的统计分析发现，煤矿安全事件舆情演化的波动性呈现出聚集效应。

（2）关于煤矿安全事件舆情演化波动性的研究适用GARCH类模型。舆情演化具有自回归特性，基于煤矿事故搜索指数建立了煤矿安全事件舆情演化的一阶自回归随机游走模型，并对模型残差进行了条件异方差即ARCH效应检验，发现煤矿事故搜索指数的波动性具有ARCH效应，因此，对煤矿安全事件舆情演化波动性的研究适用GARCH类模型。

（3）TARCH模型对煤矿安全事件舆情演化波动性的把握优于GARCH模型。实证结果表明，GARCH（1，1）模型和TARCH（1，1）模型都成功地刻画了煤矿安全事件舆情演化的波动性特征，并均克服了煤矿事故搜索指数自回归方程残差序列存在的条件异方差性。相比较而言，TARCH（1，1）模型考虑了好消息和坏消息对煤矿安全事件舆情演化波动性影响的不同，发现好消息能够降低煤矿安全事件舆情演化的波动性；同时，TARCH（1，1）模型对煤矿安全事件舆情演化波动性的形态和程度的模拟都优于GARCH（1，1）模型。

［1］ Zakoian，J.M..Threshold Heteroskedastic Models［J］.Journal of Economic Dynamics and Control，1994（18）

［2］ Basel，M.A.，Valentina Corradi.Predicting the Volatility of the S&P-500 Stock Index via GARCH Models:the Role of Asymmetries［J］.International Journal of Forecasting，2005（1）

［3］ Md.Sabiruzza-man，etc..Modeling and Forecasting Trading Volume Index:GARCH versus TGARCH Approach［J］.The Quarterly Review of Economics and Finance，2010（2）

［4］ Liu，Hung-Chun，Hung Jui-Cheng.Forecasting S&P-100 Stock Index Volatility:The Role of Volatility A-symmetry and Distributional Assumption in GARCH Models［J］.Expert Systems with Applications，2010（7）

［5］ 岳朝龙.上海股市收益率GARCH模型族的实证研究［J］.数量经济与技术经济研究，2002（4）

［6］ 陈千里，周少甫.上证指数收益的波动性研究［J］.数量经济技术经济研究，2002（6）

［7］ 刘金全，崔畅.中国沪深股市收益率和波动性的实证分析［J］.经济学，2002（1）

［8］ 刘晓，李益民.GARCH族模型在股市中的应用——深圳成分指数波动性研究［J］.技术经济与管理研究，2005（5）

［9］ 顾锋娟，岑仲迪.基于GARCH类模型和SV类模型的沪深两市波动性研究［J］.数学的实践与认识，2011（1）

［10］ 张金林，贺根庆.中国创业板和主板市场时变联动与波动溢出［J］.中南财经政法大学学报，2012（2）

［11］ 杨晨辉，刘新梅.宏观经济信息发布对沪深300指数波动性的影响［J］.山西财经大学学报，2012（3）

［12］ 万源.基于语义统计分析的网络舆情挖掘技术研究［D］.武汉理工大学，2012

［13］ 余品锐，刘天桢.基于GARCH模型的网络新闻与舆情的波动性分析［J］.计算机与现代化，2012（8）

Research on volatility of public opinion of coal mine safety incidents based on GARCH model

Zhang Hua1，Yang Xue2，Li Songhua2，Wang Fei2
（1.China University of Mining&Technology，Beijing，Haidian，Beijing 100083，China；2.North China University of Water Resources&Electric Power，Zhengzhou，Henan 450045，China）

GARCH econometric model is used to analyze volatility characteristics of public opinion evolution of coal mine safety incidents.Based on an empirical study on weekly average data of coal mine incidents from January 1，2011 to May 16，2014 in Baidu search index，it can be found that:the volatility of public opinion evolution of coal mine safety incidents shows aggregation effect；the model residual error is examined by ARCH effect，and it shows that the volatility of coal mine incidents search index has ARCH effect.Therefore，GARCH model is applicable to the study on the volatility of public opinion evolution of coal mine safety incidents，and the model results can provide prerequisite information for the warning of public opinion of coal mine safety incidents.

GARCH model，coal mine safety，public opinion，volatility

TD-9

A

张华（1974-），女，河南洛阳人，管理学博士，中国矿业大学（北京）博士后，主要从事安全科学研究。

（责任编辑 张大鹏）

2012年度国家社科基金青年项目——煤矿动态安全预警与关联管理问题研究（12CGL101），2013年河南省重点科技攻关计划项目——基于GIS煤矿安全三维仿真平台关键技术研究（132102310443），2014年河南省高等学校哲学社会科学创新团队支持计划（2014-CXTD-10），2015年国家自然科学基金面上项目“高危行业员工不安全情绪的预防、控制与疏导——基于情感事件、情绪承受与情绪承载管理的实证研究”（71573086）的阶段性成果