从一题多解谈发散思维

王莉

摘 要：以一个很经典的例题作引子，以一题多解的形式，试图探索解题中发散思维的应用，期待能抛砖引玉。

关键词：数学;发散思维;一题多解

现代教育，以培养学生的创造力为首要目标，而测定创造力的主要标志之一便是发散性思维，因此，培养学生的发散性思维，是一个很重要的课题。而一题多解，无疑可以锻炼发散思维，培养创造性。本文力图从一题多解出发，探索发散思维的培养。

我们先来看一道极为经典的例题的多种解法。

例题：已知：如图1所示，ABCD为长方形，短边与长边之比为1∶3;两条长边分别被分成三等份，各等分点联结如图。

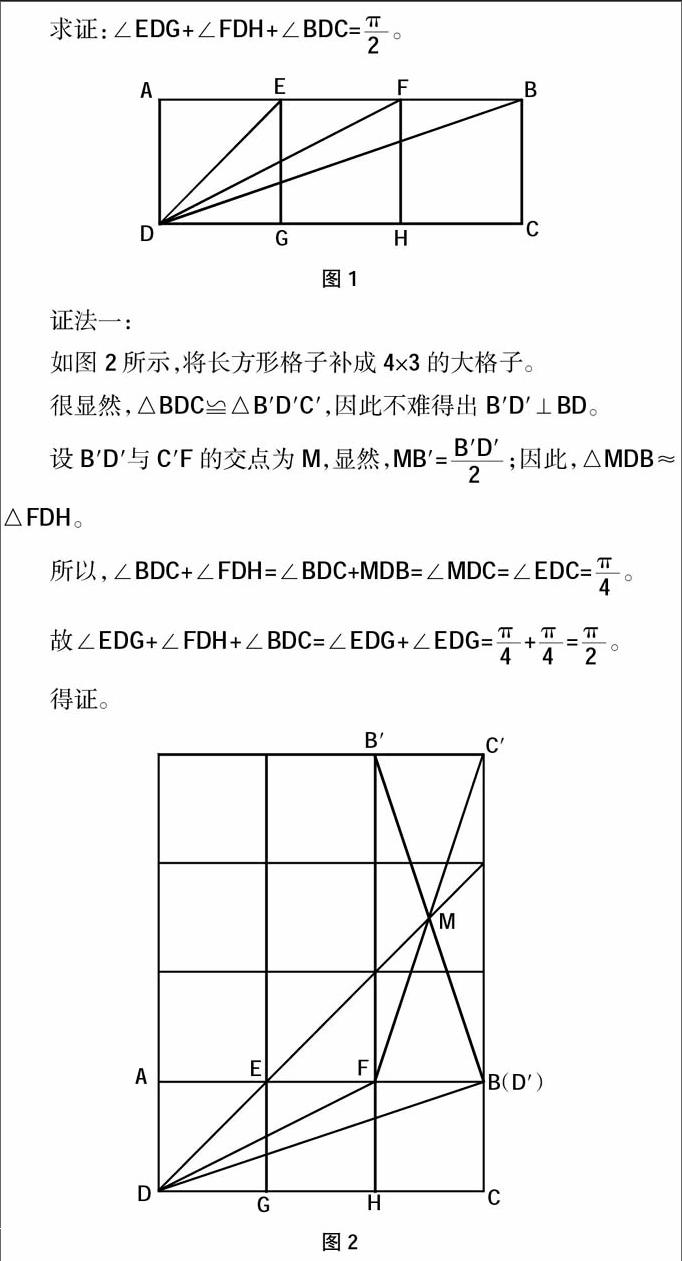
求证：∠EDG+∠FDH+∠BDC=。

[A][B][C][D][E][F][G][H]

图1

证法一：

如图2所示，将长方形格子补成4×3的大格子。

很显然，△BDC≌△B′D′C′，因此不难得出B′D′⊥BD。

设B′D′与C′F的交点为M，显然，MB′=;因此，△MDB≈△FDH。

所以，∠BDC+∠FDH=∠BDC+MDB=∠MDC=∠EDC=。

故∠EDG+∠FDH+∠BDC=∠EDG+∠EDG=+=。

得证。

[A][C][D][E][F][G][H][B（D′）][M][B′][C′]

图2

证法二：

由题设，不难得知：

tan（∠BDC）=;tan（∠FDH）=;tan（∠EDG）=1;由和角

公式：

tan（∠BDC+∠FDH）==

=1;

由题图得知：0<∠BDC<∠FDH<∠EDG=，从而

0<∠BDC+∠FDH<;故

∠BDC+∠FDH=∠EDG=;从而

∠BDC+∠FDH+∠EDG=+=。

得证。

证法三：

由复数的乘法公式，复数的乘积的辐角，等于复数的辐角的和。联想到题中所要证明的正是三个角度的和，因此，证法三油然而生。

由（3+i）（2+i）（1+i）=（5+5i）（1+i）=5（1+i）2=10i

由题图得知：0<∠BDC<∠FDH<∠EDG=;

所以，0<∠BDC+∠FDH+∠EDG<;

因此∠BDC+∠FDH+∠EDG=。

得证。

至此，证法一运用三角形相似及全等、证法二运用三角函数、证法三运用复数运算，分别从不同的角度出发，运用不同的知识，殊途同归，完美地解决了问题，这正是发散思维的魅力之所在。

参考文献：

[1]谢恩泽，赵树智.数学思想方法纵横论[M].北京：科学出版社，1987.

[2]黄兴赞，浅谈数学创造发散思维能力的培养[J].科学时代，2014（07）.

·编辑 王团兰