基于增广节点支路关联矩阵的前推回代潮流算法

张万月，陈星莺，2，余昆，2，沈培锋

（1.河海大学能源与电气学院，江苏南京　210098；2.江苏省配用电与能效工程技术研究中心，江苏南京　210098；3.南京供电公司，江苏南京　210019）

基于增广节点支路关联矩阵的前推回代潮流算法

张万月1，陈星莺1，2，余昆1，2，沈培锋3

（1.河海大学能源与电气学院，江苏南京210098；2.江苏省配用电与能效工程技术研究中心，江苏南京210098；3.南京供电公司，江苏南京210019）

含多电源的配电网进行优化调度分析时，对多个电气岛的潮流并行计算可提高计算效率。为了满足故障隔离、网络重构的需要，配电网在运行中会出现电气岛的供电区域及路径的改变，给配电网的拓扑分析及潮流计算带来麻烦。提出了基于增广节点支路关联矩阵的拓扑分析方法，该方法在基本的节点支路关联矩阵中增加了联络开关所在支路的信息，可以在不对节点重新编号的情况下分析拓扑改变后配电网的支路层次，还可以判断配电网是否有环、孤岛的存在，并为并行分析含多电气岛的配电网提供了基础。与前推回代法结合，可灵活计算配电网潮流，以支路功率的正负表示其实际流向。该方法简单、高效，并以IEEE-69节点算例验证了所提方法的正确性。

配电网重构；拓扑分析；潮流计算；增广节点支路关联矩阵

智能配电网呈网格化结构，用户可以从多个电源获得电能，其中包括主电源、分布式电源［1］（distributed generation，DG），由于国家文件规定对清洁能源发电要保障性收购，配电网中的DG以清洁能源发电为主。对配电网的优化调度［2］需要计及多个电源的影响，而潮流计算是其中的基础。

配电网中存在大量的开关，通过对开关的操作实现故障隔离、网络重构及自愈控制等功能，但开关的动作可能会使拓扑发生变化，甚至电网会解列为若干个相互没有电气联系的电气岛。配电网的另一个特点是结构与输电网不同，使经典潮流算法如牛拉法、PQ分解法不易收敛［3-4］。适合配电网特殊结构的前推回代潮流计算方法经不断完善，已成为配电网潮流计算的主要方法［5］。但前推回代法中电量的计算有严格的顺序［6］，不能适应网络的拓扑改变。针对此问题，有文献提出了部分解决方法，如基于节点分层的前推回代方法［7］，采用有向图矩阵来识别拓扑改变［8］，采用节点-分层关联矩阵［9］，基于“短接”操作的配电网拓扑分析算法［10］。但是上述方法没有介绍如何判断环路、孤岛的存在，且需要形成过多辅助矩阵，编程复杂；不能对多个电气岛并行分析。

本文提出了基于增广节点支路关联矩阵（augmented node branch incidence matrix）的拓扑分析方法，该方法在基本的节点支路关联矩阵［11］中增加了联络开关所在支路的信息，可以在不对节点重新编号的情况下分析拓扑改变后配电网的支路层次，还可以判断配电网是否有环、孤岛的存在，并为并行分析包含主电源、DG供电的多电气岛的配电网提供了基础。不需要形成过多的辅助矩阵，通过搜索判断上下层支路的连接关系，与前推回代法结合，可灵活计算配电网潮流，以支路功率的正负判断潮流的实际流向，以扩展IEEE-69节点算例验证了所提方法的有效性。

1　配电网拓扑分析

1.1支路层次判断

不失一般性，以图1为例说明本方法。

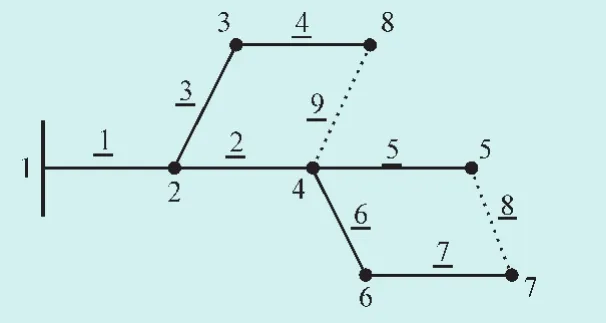
图1　8节点配电网（带下划线的为支路标号）Fig.1　8 Node distribution network

首先，根据网络拓扑信息容易形成增广节点支路关联矩阵A。设网络节点数为x，正常运行时支路数为y，联络开关数为z，则可形成一个x（y+z）阶的增广节点支路关联矩阵。将联络开关所在的支路也保存在此矩阵中，可灵活地分析网络拓扑改变后支路层次关系。矩阵第i行j列元素为1，表示节点i与支路j直接相连。图1所示的配电网的增广节点支路关联矩阵如图2所示，矩阵为8行9列。

图2　增广节点支路关联矩阵Fig.2　Augmented node branch incidence matrix

其中：行表示节点1～8，列表示支路1～9。

其次，将断开的开关所在的列置零，在初始状态下，开关8与开关9为断开状态，则将第8列、第9列置零，从根节点1开始搜索，搜索的流程见图3。

图3　寻找支路层次的流程图Fig.3　Flowchart for finding the branch-level

在图3中可看到在搜索的过程中有两种情况结束搜索：一是当网络为连通图时，可以搜索到所有支路，并将增广节点支路关联矩阵中的“1”全部置“0”；二是当网络存在孤岛时，搜索到所有连接在根节点即本电气岛的支路，虽然此时增广节点支路关联矩阵中仍然存在“1”元素，但是依然退出搜索。

搜索得到结果即为支路层次矩阵。其行数代表支路的层数，每一层的非零元素代表在该层次支路的号码，对于图1所示的简单网络，可以观察验证支路层次矩阵的正确性，如图4所示。

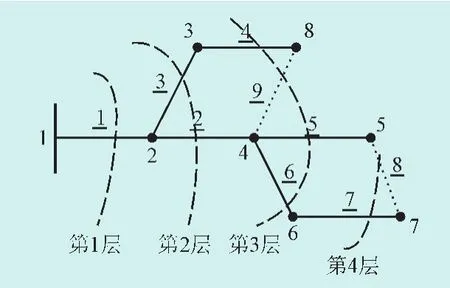
图4　8节点配电网的支路层次Fig.4　The branch-level of the 8 node distribution network

1.2存在孤立支路时的支路层次判断

如在图1中，若将支路2、4断开，则将矩阵A的2、4列置零，记为A′，采用图3的流程图对A′进行支路层次分析得到支路层次矩阵为：

若支路层次矩阵中的非零元素的个数之和小于配电网正常运行时支路的个数，则存在孤立的支路。

1.3判断环路的存在

在网络重构的寻优过程中，可能产生环路［12-13］，而这是一种不被允许的运行状态，需要对这种状态进行识别。如支路3、4断开时，将矩阵A的3、4列置零，记为A″，采用图3的流程图对A″进行支路层次分析得到支路层次矩阵为：

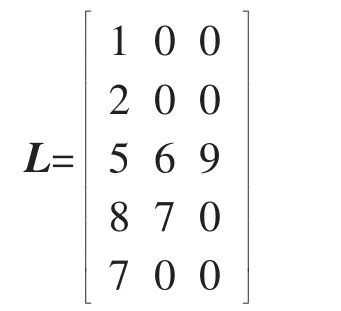
其中支路7出现了2次，可知存在环路。并且有一条规则：

有m个支路的编号在支路层次矩阵中出现了2次，则拓扑存在m个环路。

1.4存在DG供电时的支路层次分析

当主电源或馈线故障时，DG可以为一部分负荷供电，提高供电的可靠性。本文所提方法也可为DG供电的支路进行拓扑分析，且以此说明对多个电气岛进行分析的方法。

假设某运行工况如图5所示，存在2个电气岛。由主电网为负荷点2、3供电，由DG为其余负荷点供电。

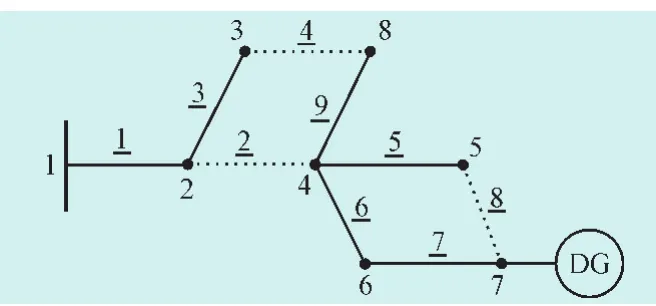
图5　主网与DG共同供电的示意图Fig.5　Distribution network with DG

在1.2小节已经分析了由主网供电的电气岛支路层次矩阵，下面分析由DG供电的电气岛支路层次矩阵。将A的第2、4、8列置零，令根节点为7，采用图3所示的流程，得出支路层次矩阵如下：

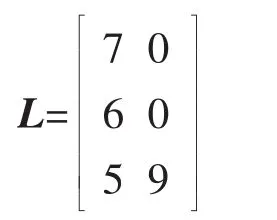
由此可见，2个电气岛的支路层次矩阵的搜索过程互不相关，因此本文方法为多电气岛拓扑的并行分析提供了基础。

2　前推回代法

将支路层次矩阵与前推回代法结合。通过搜索支路层次矩阵的相邻层判断支路的连接关系，通过标志位的设置判断支路潮流的流向，首先作如下约定：

约定潮流的正方向为从支路的首节点流向末节点；如果潮流从末节点流向首节点，则以负号标注。

结合前推回代法的特点，并考虑配电网拓扑的改变，图6所示配电网节点与支路的原始数据采用下面的格式：

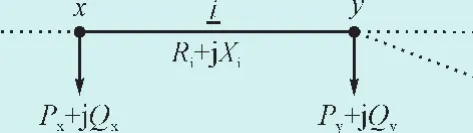
图6　节点与支路的参数示意图Fig.6　Schematic diagram of the network parameters

节点参数矩阵：

式中：x为节点号码；Px，Qx分别代为点x的有功、无功功率；u，δ分别为节点x的电压模值与相角。

支路参数矩阵：

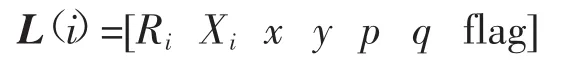
式中：i为支路号码；Ri，Xi分别为支路i的电阻、电抗信息；x，y分别为支路i的首末节点；p，q分别为支路实际流通方向前端的功率；flag为标志位，为0表明此支路潮流为正向，从支路的首节点流向末节点，为1则是反向。

2.1标志位的设置

由标志位来判断配电网潮流的实际流向。仅相邻的两层可能存在连接关系，且只存在4种情况：

1）L（i）.y=L（j）.x，两支路的标志位置0；

2）L（i）.y=L（j）.y，支路i标志位置0，支路j置1；

3）L（i）.x=L（j）.y，支路i，j标志位置1；

4）L（i）.x=L（j）.x，支路i标志位置1，支路j置0。

上述4种情况中，支路i为任一条除最后一层的支路，支路j为与之相邻的下层的支路。从第一层开始向下遍历搜索，可以得到每条支路的标志位。

2.2前推功率

对于最后一层支路，流程如下：

判断标志位flag。如果flag=0，表明潮流从首节点流向末节点，采用下面两式计算：

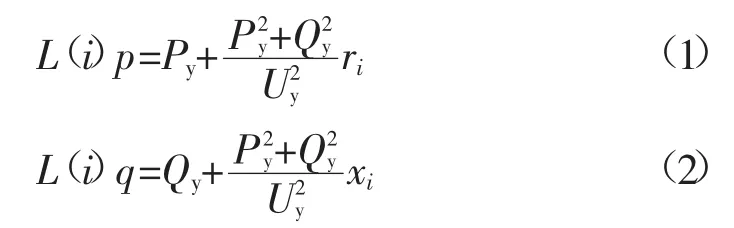
如果flag=1，表明潮流从末节点流向首节点，计算形式相同，只需将其中的下标y改为x即可。

其中，L（i）p，L（i）q分别为支路i实际流向的首端的有功，无功；Py，Qy分别为支路i末端节点的负荷有功，无功；Px，Qx分别为支路i首端节点的负荷有功，无功；Uy，Ux为支路i末端、首端节点的电压模值，第一次迭代采用额定值，之后的迭代采用上一次迭代计算得到的电压值。

对于其他层的支路，因为其下一层可能有支路与其连接，所以在计算支路实际流向首端功率的时候也需将其下层所连接的支路的功率加上，如下所示：

判断标志位flag。如果flag=0，表明潮流从首节点流向末节点，采用下面四式计算：

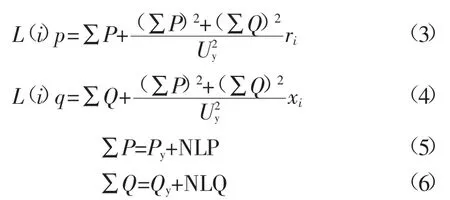
如果flag=1，表明潮流从末节点流向首节点，计算形式相同，同样只需将其中的下标y改为x即可。

其中，∑P，∑Q分别为支路实际流向的末端的功率；NLP，NLQ分别为与本支路相连接的下层支路的功率，以NLP为例，说明计算方法：

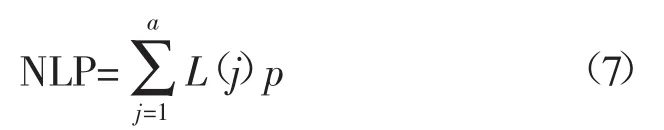
式中：a为相邻下层支路与支路i相连接的支路数，将4种连接方式的任意一种，都计算在内。

2.3回代电压

回代电压的步骤较简单，从支路层次矩阵的第一行开始，依次向下层计算：

判断支路的flag，如果flag=0

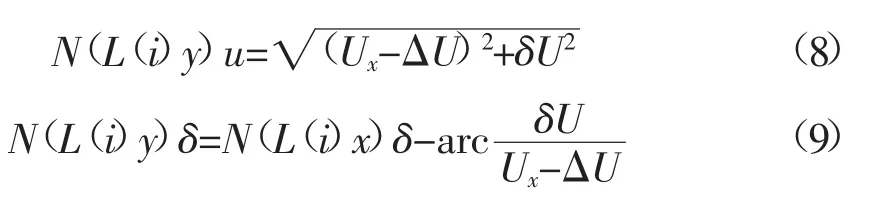
如果flag=1

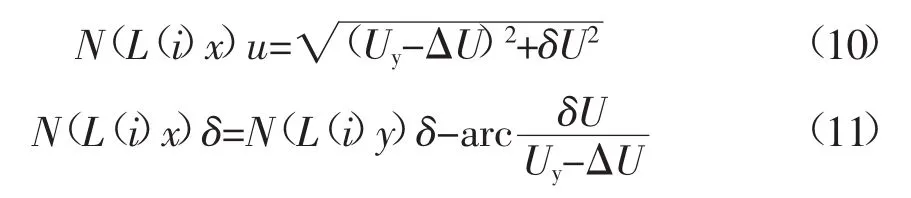
式中：N（L（i）y）u，N（L（i）x）u分别为支路i末端节点、首端节点的电压幅值；N（L（i）y）δ，N（L（i）x）δ分别为相应的电压相角；ΔU，δU分别为电压降落的纵分量、横分量。

上面将全部的迭代公式列出，按照上述的公式进行迭代，直到达到收敛精度：

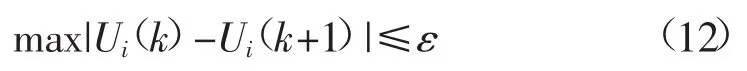
式中：k为迭代次数；ε为收敛精度。

计算完毕，依据支路flag对支路的功率进行处理，若flag为0，输出正的支路功率，若flag为1，输出负的支路功率，从而在结果中表明潮流的流向。

3　算例分析

3.1算例1：拓扑改变后的潮流计算

算例1是IEEE-69节点标准算例，详见文献［14］。其接线图如图7（a）所示，联络开关由虚线表示。网络重构前的初始网络为开关｛69，70，71，72，73｝断开，采用本文方法计算潮流只需要将增广节点支路关联矩阵的相应列置零即可。图7（b）为网络重构的一个备选解，断开的开关为｛18，13，56，8，61｝，计算时将增广节点支路关联矩阵的相应列置零，2种运行状态的潮流计算结果见表1。

表1中的计算结果为标幺值，其基准值为12.66 kV，10 MV·A。由结果可知，图7（b）网络的支路功率存在负值，因为在约定的参考方向下，其潮流流向为反向。

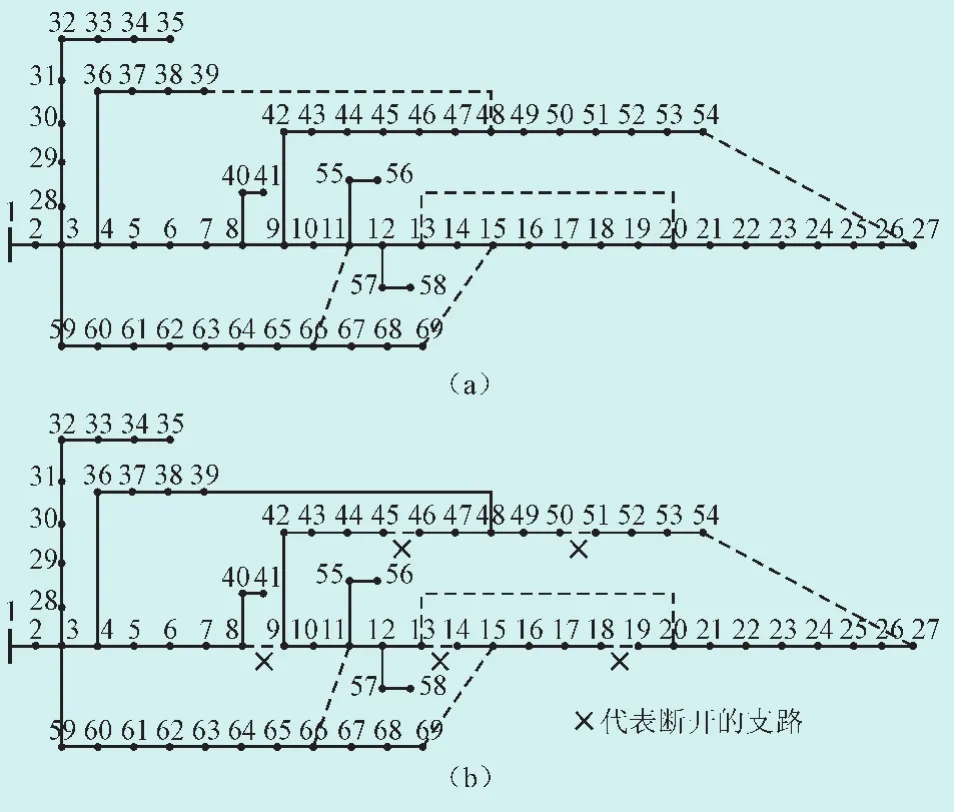
图7　IEEE-69节点配电网Fig.7　IEEE-69 node distribution network

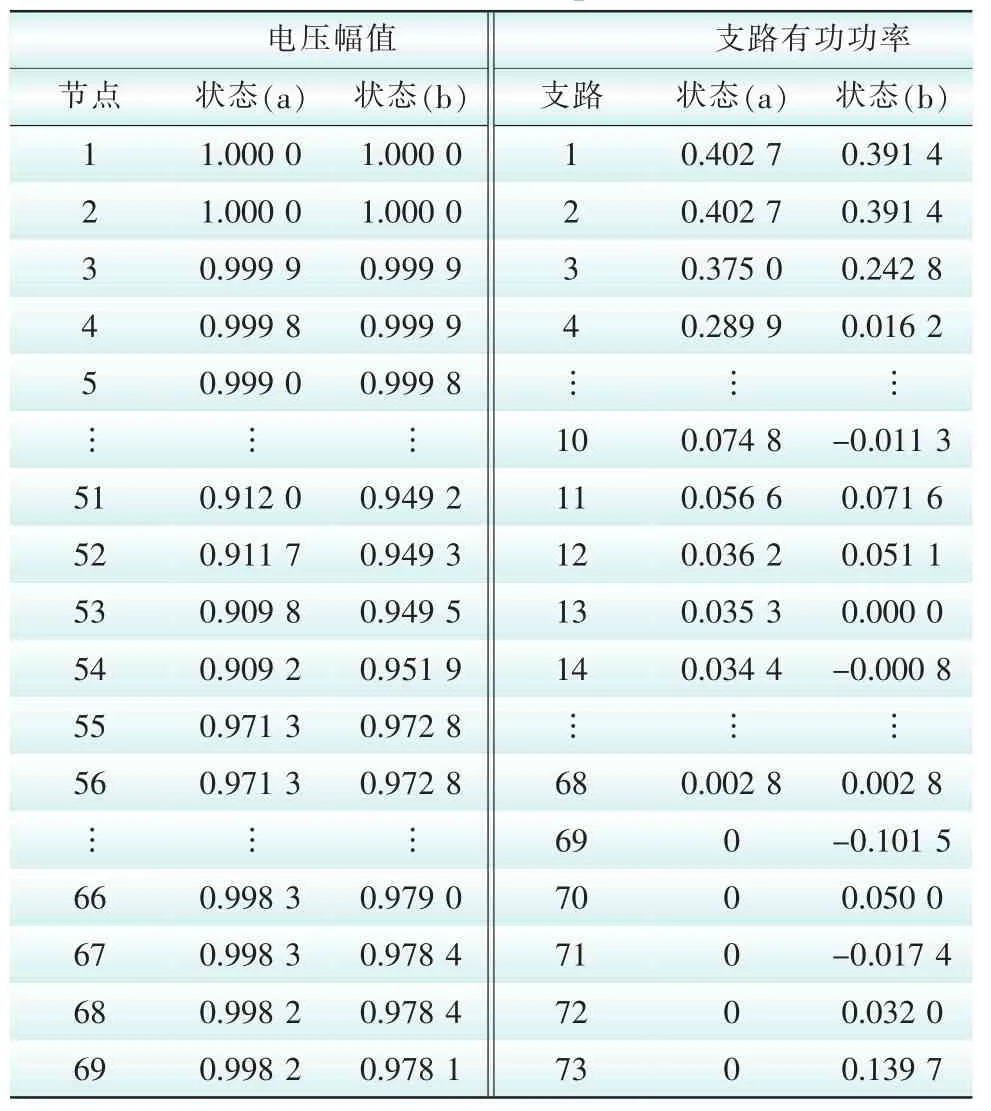
表1　2种运行状态下潮流计算的结果Tab.1　Calculation results of the power flow in two states

3.2算例2：含DG的潮流计算

在算例1图7（b）的基础上在节点23加上DG，假设线路70存在故障，则负荷｛19，20，21，22，23，24，25，26，27，51，52，53，54｝需要由DG供电，并认为DG的容量足够大，可作为其供电区域的平衡节点。此时存在两个电气岛，需要2次拓扑分析，首先将增广节点支路关联矩阵的｛18，13，56，8，61，70｝列置零，以节点1为根节点，搜索到由主电源供电的支路层次，再以节点23为根节点，搜索到由DG供电的支路层次。计算结果见表2。

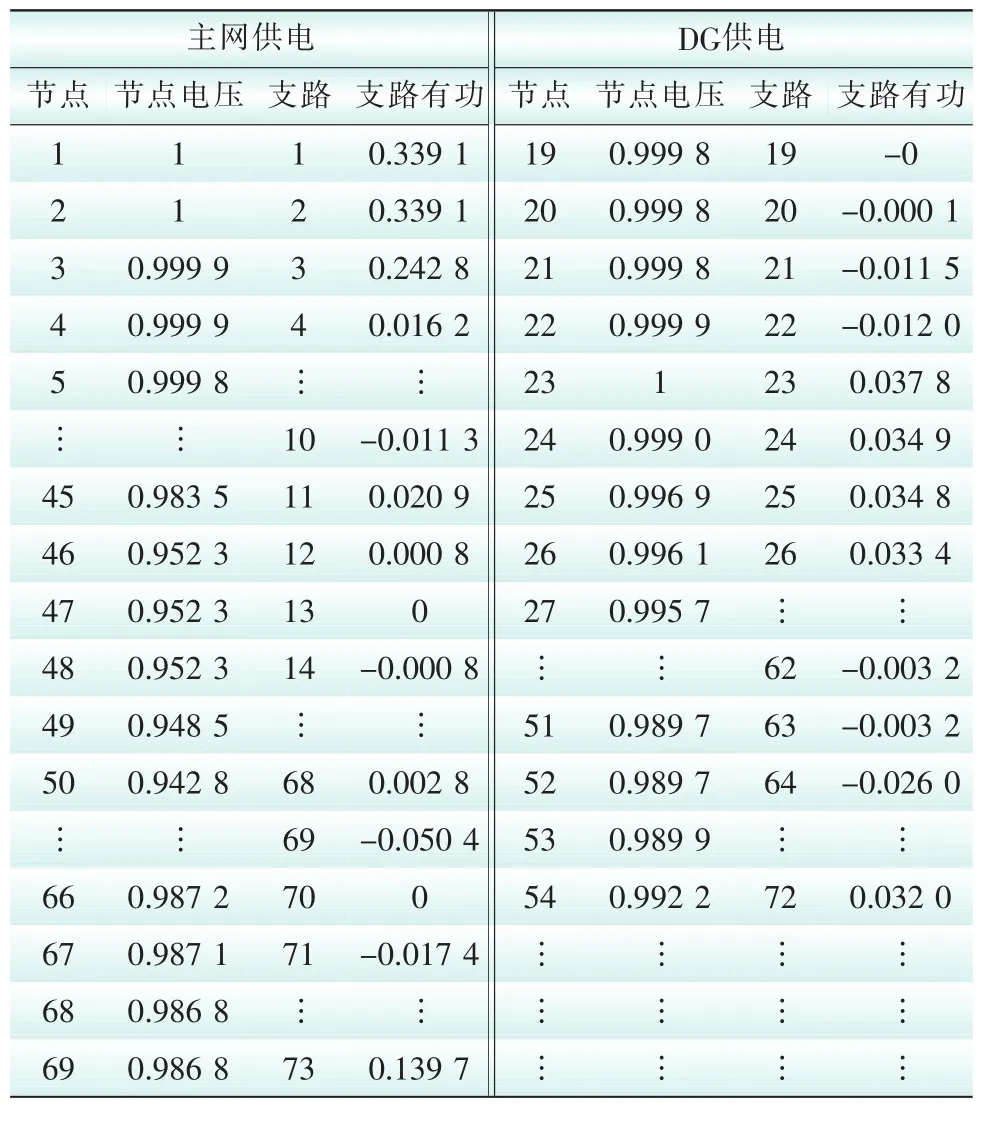
表2　含DG供电的潮流计算结果Tab.2　Power flow with DG

4　结语

本文提出了基于增广节点支路关联矩阵的拓扑分析方法，可以在不对节点重新编号的情况下分析拓扑改变后配电网的支路层次，还可以判断配电网是否存在环、孤岛，并为并行分析包含主电源、DG供电的多电气岛的配电网提供了基础。不需要形成过多的辅助矩阵，通过搜索判断上下层支路的连接关系，与前推回代法结合，可灵活计算配电网潮流，以支路功率的正负表示其实际流向，并以扩展IEEE-69节点算例验证了所提方法的有效性。

［1］王成山，李鹏.分布式发电、微网与智能配电网的发展与挑战［J］.电力系统自动化，2010，34（2）：10-14，23.WANG Chengshan，LI Peng.Development and challenges of distributed generation，the micro-grid and smart distribution system［J］.Automation of Electric Power Systems，2010，34（2）：10-14，23（in Chinese）.

［2］陈星莺，陈楷，刘健，等.配电网智能调度模式及关键技术［J］.电力系统自动化，2012，9（25）：22-26.CHEN Xingying，CHEN Kai，LIU Jian，et al.A distribution network intelligent dispatching mode and its key techniques［J］.Automation of ElectricPowerSystems，2012，9（25）：22-26（in Chinese）.

［3］刘莉，赵璇，姜新丽.基于层次矩阵的配电网拓扑分析与潮流计算［J］.电力系统保护与控制，2012，40（18）：91-94，100.LIU Li，ZHAO Xuan，JIANG Xinli.Distribution network topology analysis and flow calculation based on layer matrix［J］.Power System Protection and Control，2012，40（18）：91-94，100（in Chinese）.

［4］张学松，柳焯，于尔铿，等.配电网潮流算法比较研究［J］.电网技术，1998，22（4）：47-51.ZHANG Xuesong，LIU Zhuo，YU Erkeng，et al.A comparison on power flow calculation methods for distribution network［J］.Power System Technology，1998，22（4）：47-51（in Chinese）.

［5］孙宏斌，张伯明，相年德.配电潮流前推回推法的收敛性研究［J］.中国电机工程学报，1999，19（7）：27-30.SUN Hongbin，ZHANG Boming，XIANG Niande，et al.Study on convergence of back/forward sweep distribution power flow［J］.Proceedings of the CSEE，1999，19（7）：27-30（in Chinese）.

［6］高亚静，苗宏佳.基于阻抗补偿的三相四线制配电网前推回代潮流算法［J］.电力系统自动化，2015，39（7）：47-51.GAO Yajing，MIAO Hongjia.An impedance compensation based forward/backward sweep power flow algorithm for three-phase four-wire distribution network［J］.Automation of Electric Power Systems，2015，39（7）：47-51（in Chinese）.

［7］李如琦，谢林峰，王宗耀，等.基于节点分层的配网潮流前推回代方法［J］.电力系统保护与控制，2010，38（14）：63-66，139.LI Ruqi，XIE Linfeng，WANG Zongyao，et al.Back/forward substitution method for radial distribution load flow based on node-layer［J］.Power System Protection and Control，2010，38（14）：63-66，139（in Chinese）.

［8］孙鹏.基于模糊多目标决策理论的城网改造方法研究［D］.北京：华北电力大学，2013.

［9］王佳佳，吕林，刘俊勇，等.基于改进分层前推回代法的含分布发电单元的配电网重构［J］.电网技术，2010， 34（9）：60-64.WANG Jiajia，LÜ Lin，LIU Junyong，et al.Reconfiguration ofdistribution network containingdistribution generation units based on improved layered forwardbackward sweep method［J］.Power System Technology，2010，34（9）：60-64（in Chinese）.

［10］刘斌，曹爱珍，刘秋榕，等.基于配电网拓扑分析的重构潮流算法［J］.电网与清洁能源，2012，28（9）：25-28.LIU Bin，CAO Aizhen，LIU Qiurong，et al.Power flow reconfiguration algorithm based on distribution network topology analysis［J］.Power System and Clean Energy，2012，28（9）：25-28（in Chinese）.

［11］王峥，丛培杰.基于改进前推回代法的辐射状配电网潮流计算［J］.东北电力技术，2008，34（2）：7-10.WANG Zheng，CONG Peijie.Power flow calculation for radial distribution network based on forward and backward substitution method［J］.Northeast Electric Power Technology，2008，34（2）：7-10（in Chinese）.

［12］李振坤，陈星莺，余昆，等.配电网重构的混合粒子群算法［J］.中国电机工程学报，2008，28（31）：35-41.LI Zhenkun，CHEN Xingying，YU Kun，et al.Hybrid particle swarm optimization for distribution network reconfiguration［J］.Proceedings of the CSEE，2008，28（31）：35-41（in Chinese）.

［13］陈春，汪沨，刘蓓，等.基于基本环矩阵与改进和声搜索算法的配电网重构［J］.电力系统自动化，2014，38（6）：55-60.CHEN Chun，WANG Feng，LIU Pei，et al.Network reconfiguration based on basic ring matrix and improved harmony search algorithm［J］.Automation of Electric Power Systems，2014，38（6）：55-60（in Chinese）.

［14］Baran M E.Optimal capacitor placement on radial distribution system［J］.IEEE Transactions on Power Systems，1989，4（1）：725-734.

（编辑徐花荣）

Augmented Node Branch Incidence Matrix Based Back/Forward Sweep Flow Calculation

ZHANG Wanyue1，CHEN Xingying1，2，YU Kun1，2，SHEN Peifeng3
（1.College of Energy and Electrical Engineering，Hohai University，Nanjing 210098，Jiangsu，China；2.Jiangsu Engineering Research Center for Distribution&Utilization and Energy Efficiency，Nanjing 210098，Jiangsu，China；3.Nanjing Power Supply Company，Nanjing 210019，Jiangsu，China）

In the process of the optimized dispatching analysis of the multi-power distribution，parallel computing of the power flow of every electrical islands can improve the computational efficiency.To meet the requirement of the fault isolation，net-work reconfiguration，changes often occur to the power supply area and path of the electrical island in the operation of the distribution network，bringing obstacles to the topology analysis and flow calculation.A topology analysis method based on Augmented Node Branch Incidence Matrix is proposed in this paper，which adds the information of the branch with the tie breaker to the basic Node Branch Incidence Matrix.The proposed method can analyze the branch-level after the topology changes without renumbering the node，and it can also check loops and islands in the network structure，and provide the foundation for the distribution network with multipower.Combined with back/forward sweep power flow algorithm，using the plus-minus sign to represent the actual flow direction，the distribution power flow can be calculated flexibly.The proposed method is simple and efficient，and the results of IEEE-69 nodes system verify the correctness of the proposed method.

reconfiguration of distribution network；topology analysis；flow calculation；augmented node branch incidence matrix

1674-3814（2015）12-0062-06

TM711

A

2015-09-29。

张万月（1991—），男，硕士研究生，主要研究方向为配电网优化运行；

陈星莺（1964—），女，博士，教授，博士生导师，研究方向为配用电规划与评估、智能配电网运行分析、配电网智能调度与控制、高效用电与节能、能源管理与能源经济。

国家高技术发展研究计划（863计划）项目（2012AA050214）；国家自然科学基金（51207047）；江苏省电力公司科技项目（J2015059）。

Project Supported by the National High Technology Research and Development of China（863 Program）（2012AA050214）；National Natural Science Foundation of China（51207047）.