空调间歇性轮停最佳控制周期研究

管国兵，王志成，辛洁晴，何津

（1.上海交通大学电力传输与功率变换控制教育部重点实验室，上海　200240；2.国网上海市电力公司金山供电公司，上海　201500）

空调间歇性轮停最佳控制周期研究

管国兵1，王志成2，辛洁晴1，何津1

（1.上海交通大学电力传输与功率变换控制教育部重点实验室，上海200240；2.国网上海市电力公司金山供电公司，上海201500）

目前对空调间歇性轮停（duty cycling control，DCC）控制周期的论证尚缺乏理论研究。提出一种以控制期空调小时平均负荷最小化为目标的控制周期论证模型；并通过算例讨论了控制期平均室外气温、室温允许波动范围、受控端热响应参量等因素对控制周期的影响。结果表明：DCC控制周期应仅由强制停机期和持续制冷期构成，为此对特定地区，控制期允许的室温波动范围和受控端热响应参量是决定DCC控制周期的决定性因素；室温波动范围、用户群制冷空间的热容和围护结构热阻越大，则DCC控制周期越大。

空调负荷控制；间歇性轮停；最佳控制周期；等值热参数模型；热舒适度

空调负荷是造成我国城市夏季高峰负荷的主导因素［1-2］。为缓解夏季电力供需矛盾，空调负荷降载控制日益受到关注。制冷机间歇性轮停控制，也称周期性启停控制或占空比控制（duty-cycling control，DCC），是空调降载控制的一种方式；对于末端不带温控器的全空气式空调系统（如商场中所使用的中央空调系统），DCC更是主要的降载控制方式。因此，对DCC控制方案的研究具有重要意义。

DCC通过对空调系统中最主要的用电设备——制冷机实施周期性启停控制，减少制冷机运行时间来达到降载目的。制冷机启停控制周期和占空比（指每一控制周期中制冷机运行时间所占比例）是DCC降载效果的两大决定因素。从国外实际案例来看，不同项目中这2个参量的取值不尽相同。例如：美国PJM区域电力市场的多家供电商在与用户签订DCC方式的直接负荷控制协议时，以半小时为控制周期并提供几种占空比方案供用户选择［3-4］；美国德州电力与照明公司实施的居民空调DCC控制项目中，取控制周期为20 min、占空比为30%；又如台湾电力公司实施的空调主机冷吨在20RT以上DCC控制项目中，取控制周期为75 min、占空比为80%［5-7］。在公布DCC方案时，各电力供应商未对控制周期、占空比的取值方法做出解释。

在DCC方案的理论研究方面，文献［8］以占空比为决策变量，提出了商务楼中央空调按热舒适度分档的控制策略，但对制冷机控制周期未予论证、只是假定为30 min；文献［9］利用最大似然估计对非降载控制情况下制冷机的自然启停占空比进行了理论研究，结果用于空调负荷预测。可见，现有相关文献都主要关注于占空比问题，而没有对制冷机启停的最佳控制周期及其影响因素做论证分析。

为此，本文对空调DCC最佳控制周期进行论证，并通过算例分析DCC控制周期的影响因素。文中基于适合居民和小型商务楼的等值热参数（equivalent thermal parameter，ETP）模型构建空调负荷模型，但对DCC控制周期的论证结果有推广到中、大型商用建筑空调制冷机的价值。

1　制冷空间的热响应模型

ETP模型通过模拟制冷空间的热交换过程，得到室温随供冷量的动态变化关系。最常用的ETP模型为1R1C模型，仅考虑围护结构传导热阻R和室内空气热容C，此时ETP模型为如下形式［2］：

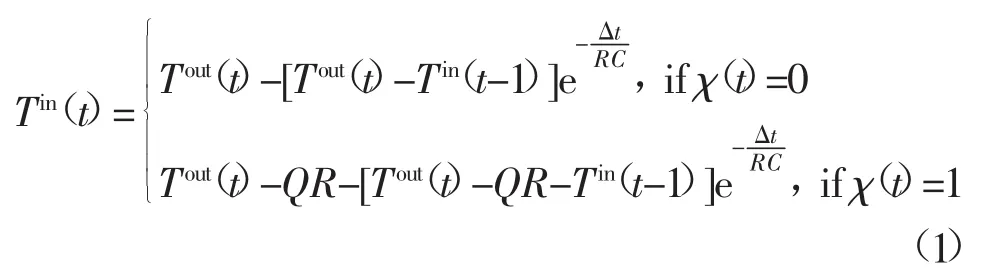
式中：χ（t）为t时刻制冷机启停状态（0表示关停、1表示开启），上、下层分别对应制冷机停机期、运行期的室温变化方程；Tin（t）、Tout（t）分别为t时刻的室内、室外温度；Δt为t至t-1时刻的时间间隔；Q、R、C为受控端热响应参量，分别表示制冷机的供冷量、围护结构热阻和室内空气热容。

若室温波动范围为［Tin1，Tin2］，根据式（1）可求得启停周期中停机期和制冷期的时长分别为

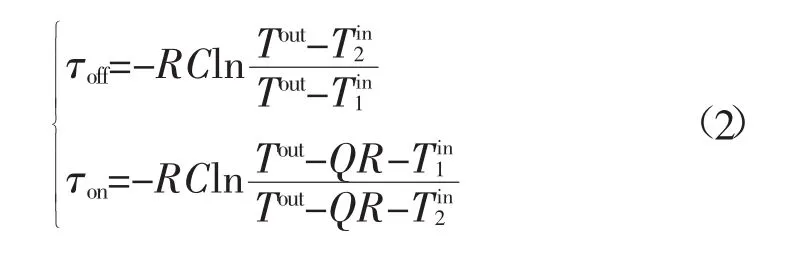
2　DCC控制下制冷机的运行方式

设用户在其习惯使用方式下，夏季空调使用期的平均室温为Tin0，由于温差控制范围作用，室温在［Tin0-ΔT，Tin0+ΔT］内波动；设用户与电力供应方事先协定的受控期室温波动范围为［Tinmin，Tinmax］，其中Tinmin= Tin0-ΔT、Tinmax=Tin2＞Tin0+ΔT。

DCC控制的特点是制冷机按一定周期启停，为此在论证控制周期和占空比时，电力供应方只能按空调控制期平均的室外气温作为气温条件（记为Tout）。在Tout条件下，根据用户习惯的日常室温波动范围［Tin0-ΔT，Tin0+ΔT］，按式（2）可确定制冷机的自然启停周期（记为τ0）和自然占空比（记为r0）。

如图1所示，在DCC控制下，每一控制周期τ中制冷机运行状态可划分为3个时段——强制停机期、持续制冷期和维持期［8］。若设r为每一周期中强制停机期以外的时间所占的比重，则：强制停机期时长τoff=（1-r）τ，此期间制冷机用电功率为0，室温从Tinmin逐步上升至Tinmax；此后制冷机启动，按额定用电功率Lcool运行直至室温下降至Tinmin，设持续制冷期时长为τz；维持期指持续制冷期结束至下一控制周期开始前的一段时间，时长为rτ-τz，此期间制冷机按τ0和r0运行，为避免室温递增的累加效应，要求每一控制周期末室温回到Tinmin，因此维持期需x个自然启停周期（x∈自然数N），该期间制冷机平均用电功率为r0Lcool、用电量为xτ0r0Lcool。

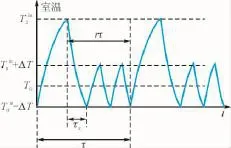
图1　制冷机每一控制周期的室温变化过程Fig.1　The changing process of room temperature loads for each refrigerator under DCC method

3　最佳周期论证模型

3.1目标函数的选择

空调负荷控制以降载为目的，但对按特定周期启停的制冷机组群而言，分钟级最大负荷由制冷机功率决定，因此控制周期的论证应当以控制期小时平均负荷的最小化为目的。

设控制期时长为H小时，忽略与制冷机启停方式关系较弱的风机、水泵用电，则控制期空调小时平均负荷峰值的最小化目标函数为

其中第h个小时的平均负为：

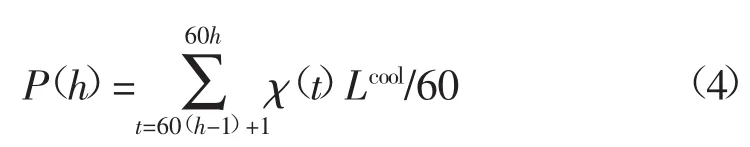
式中：第t分钟制冷机的启停状态按下式确定，

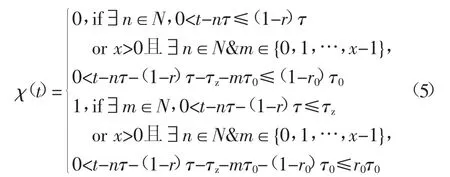
鉴于小时平均负荷等于小时用电量与60 min的比值，式（3）～式（5）等同于下述用电量最小化目标，其中控制期空调用电量由持续制冷期和维持期的制冷机用电量构成：

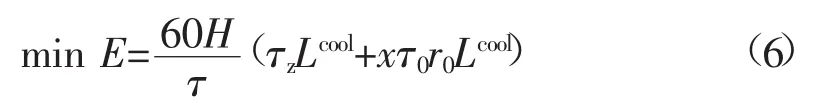
3.2约束条件

制冷机DCC过程中需兼顾热舒适度、降载需求和制冷机启停的技术性约束，具体包括：

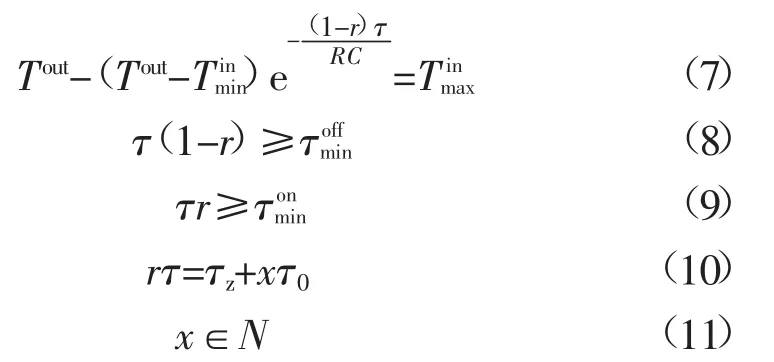
其中：式（7）要求每一停机期末的室温达到协定的上限值，这一方面是为了满足用户对室温波动范围的热舒适度要求，另一方面则是为了充分利用允许的室温波动范围、尽可能挖掘降载潜力；式（8）和式（9）分别为制冷机最小停机时间约束和最小开机时间约束［8］；式（10）和式（11）表示非强制制冷期可能包括持续运行期和维持期，且维持期包含整数个自然启停周期，使控制周期末的室温回到Tinmin。

决策变量包括τ、r和x，属混合整数规划问题，采用改进二进制粒子群算法求解［10］。

4　算例讨论

设某地空调控制期为异常高温日10：00—15：00，该时段平均气温38℃，某参与DCC的居民空调用户群习惯的空调制冷温度为24℃，温控偏差±1℃，协定的控制期室温上限Tinmax=28℃。设空调受控端数为10万，受控端热响应参量平均值为Q=6 750 W（能效比2.7）、R=5.56 C/kW、C=0.18 kW·h/℃［1］。利用上述参数，据式（2）算得τ0=14 min、r0=0.36，每一周期中的停机期为8.96 min、制冷期为5.04 min。

4.1最佳启停周期结果分析

优化得x=0，τ=36 min，r=0.33，对应强制停机期约24 min，持续制冷期12 min，无维持期。

在后续摄动分析中发现，Tinmax等参量的改变虽然会引起τ和r的变化，但总是保持x=0。这是因为，室温波动范围放大后，强制停机期和持续制冷期虽均大于自然启停周期中的停机期和制冷期，但制冷期增长不如停机期明显。因此尽快进入下一轮强制启停周期要比维持若干周期的自然启停更为降载。

4.2最佳启停周期影响因素分析

4.2.1控制期平均室外气温的影响

保持其他参量不变，仅改变控制期平均室外气温Tout，得到τ、r和小时平均负荷降载率随Tout的变化曲线，如图2、3所示。从中可见：

图2　控制周期和占空比随室外气温的变化Fig.2　Relationship of τ and r with the outdoor temperature

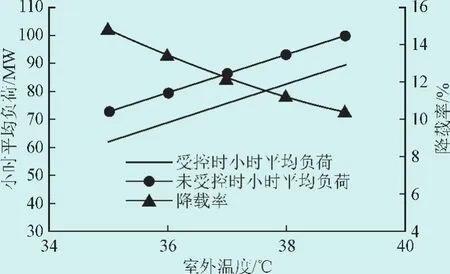
图3　小时平均负荷及其降载率随室外气温的变化Fig.3　Relationship of the hourly average load and load clipping rate with the outdoor temperature

1）随着平均气温的降低，τ增大而r减小。这是因为Tout下降时单位时间内制冷空间的得热量减小，停机期室温上升速率变慢、制冷期室温下降速率变快，但因制冷期的供冷量远大于得热量，温降时间的变化不如温升时间的变化明显，因而启停周期延长而其中持续制冷期所占比例降低。

2）平均气温降低时，因得热量减小，制冷机无论在自然启停还是DCC方式下的小时平均负荷均减小，降载量基本不变，降载率增大。

4.2.2室温波动范围的影响

保持其他条件不变，改变控制期室温允许上限值Tinmax，考察τ、r和小时平均负荷降载率随Tinmax的变化，如图4、5所示。从中可见：

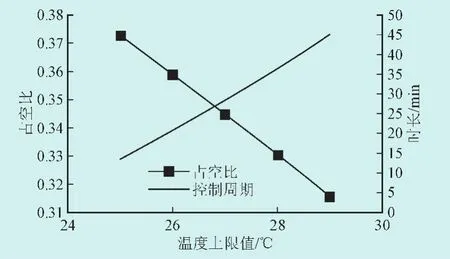
图4　控制周期和占空比随室温上限值的变化Fig.4　Relationship of τ and r with the upper limit of room temperature

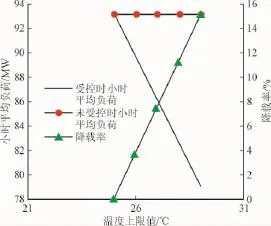
图5　小时平均负荷及其降载率随室温上限值的变化Fig.5　Relationship of the hourly average load and load clipping rate with the upper limit of room temperature

1）随着Tinmax增大、控制期室温波动范围增大，τ增大而r减小。造成上述现象的原因同样是因为制冷期供冷量远大于得热量，故室温波动范围增大时停机期时长增长较制冷期明显。

2）随着Tinmax增大、空调小时平均负荷下降，使得降载量和降载率都有所增加。

4.2.3热响应参量的影响

（1）制冷量Q的影响

改变Q的物理意义是调节制冷机制冷功率，在其他参量不变的条件下改变Q则对应着受控端制冷功率多投/欠投情况。τ、r和小时平均负荷降载率随Q的变化如图6、7所示。从中可见：

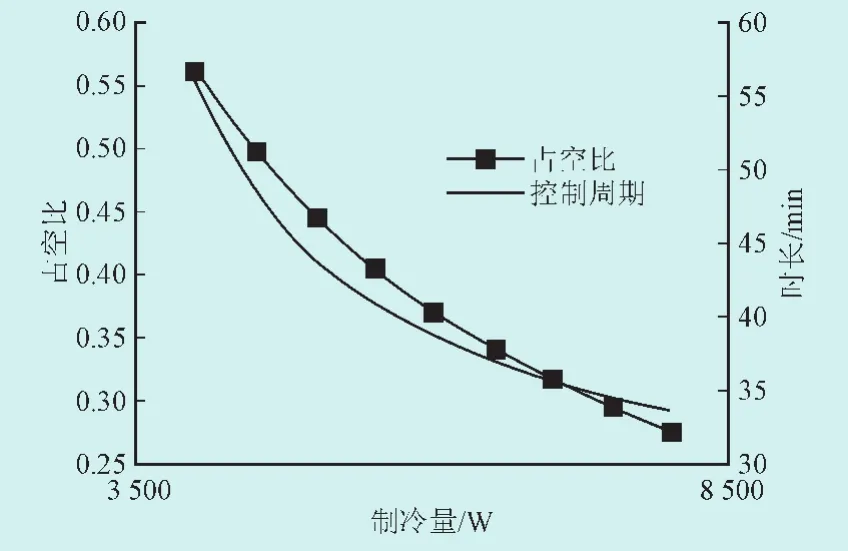
图6　控制周期和占空比随制冷量Q的变化Fig.6　Relationship of τ and r with Q

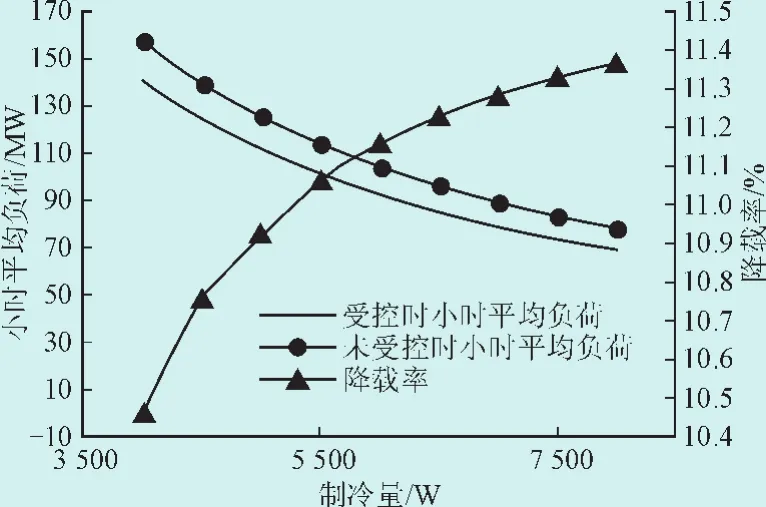
图7　小时平均负荷及其降载率随制冷量Q的变化Fig.7　Relationship of the hourly average load and load clipping rate with Q

1）随着Q增大，制冷期温降越快，而停机期时长不受影响，故而τ和r均减小。

2）由于温降速度加快、占空比减小，自然启停和DCC方式下的小时平均负荷没有随Q增大而增大、反而有所减小，降载量基本不变、降载率上升。

（2）热容C的影响

热阻C的摄动意味着建筑制冷空间蓄热能力的变化。τ、r和小时平均负荷降载率随C的变化如图8、9。从中可见：

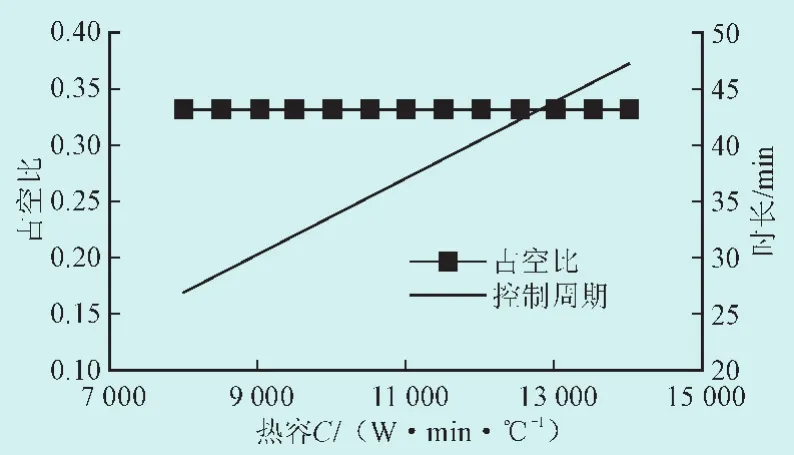
图8　控制周期和占空比随热容C的变化Fig.8　Relationship of τ and r with C

1）热容C越大，τ越大而r不变。这说明C越大，制冷空间蓄热能力越强，但这种变化对停机期温升速率和制冷期温降速率的影响相同。

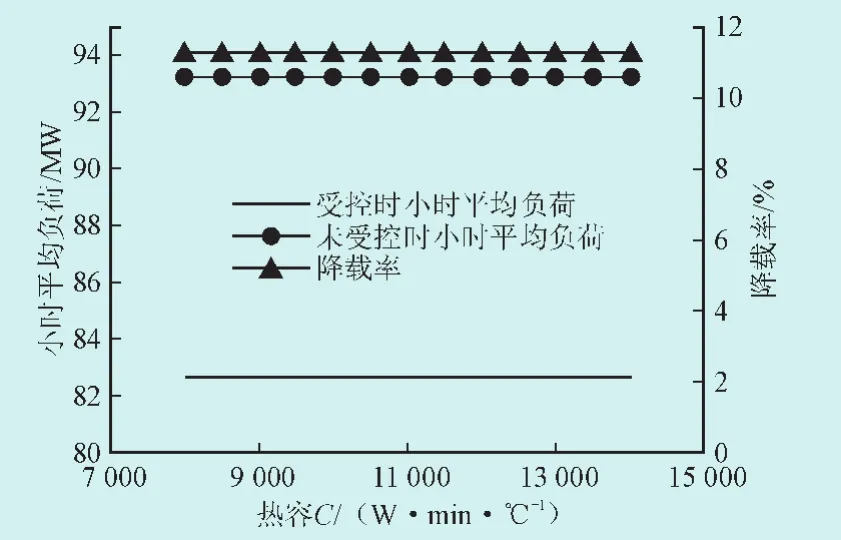
图9　小时平均负荷及其降载率随热容C的变化Fig.9　Relationship of the hourly average load and load clipping rate with C

2）自然启停和DCC方式下空调小时平均负荷和降载率均不随C的变化而变化。这是因为r不变、从而每一小时内制冷机的用电量保持不变。

（3）热阻R的影响

改变R的物理意义是改变制冷空间围护结构的热传导性能。热阻R越大，单位时间里通过围护结构热传导进入室内的热量越小，τ越大、r越小、降载率越大，作用规律同外界气温的影响。

5　结语

本文对空调DCC控制方式提出一种最佳控制周期论证的优化模型，并通过摄动分析探讨了最佳控制与其影响因素之间的关系。算例结果表明：

1）为获得尽可能大的小时平均负荷降载量，DCC控制周期仅由强制停机期和持续制冷期构成，不应设置维持期。

2）由于不设置维持期，对于特定地区的特定用户群，DCC控制周期主要由用户允许的控制期室温波动范围决定，室温波动范围越大则？增大而r减小，具体取值可按文中式（2）计算。

3）外界气温对DCC方案的影响也较大，在越是炎热的地区实施DCC，制冷机间歇性启停的周期越小、占空比越大。

4）不同用户群因制冷功率大小、制冷空间大小、围护结构的差异，热响应参量有所不同，对应一定室温调节范围的DCC控制周期和占空比也有所不同。因此，宜对不同用户群（如区分居民和商业建筑）实施不同的DCC方案。据本文测算结果，居民空调的DCC周期在30 min左右，而C取值较大的商业建筑中央空调的DCC控制周期应比居民空调大。

［1］李扬，王治华，卢毅，等．南京市夏季气温-日峰荷特性分析［J］．电网技术，2001，25（7）：63-66，71．LI Yang，WANG Zhihua，LU Yi，et al.Characteristic analysis of summer air temperature-daily peak load in Nanjing［J］.Power System Technology，2001，25（7）：63-66，71（in Chinese）．

［2］周磊，李扬，高赐威．聚合空调负荷的温度调节方法改进及控制策略［J］．中国电机工程学报，2014，34（31）：5579-5589．ZHOU Lei，LI Yang，GAO Ciwei.Improvement of temperature adjusting method for aggregated air-conditioning loads and its control strategy［J］.Proceedings of the CSEE，2014，34（31）：5579-5589（in Chinese）．

［3］Pepco Energy Wise Rewards［EB/OL］.（2013-07-21）［2015-07-03］.https：//energywiserewards.pepco.com/．

［4］RYAN N E，BRAITHWAIT J T，SMITH B A．Generalizing direct load control program analysis：implementation of the duty cycle approach［J］．IEEE Transactions on Power System，1989，4（1）：293-299．

［5］SCHNEIDER K，THEDFORD M．Evaluation of a local air conditioning duty cycling device as a load management tool［J］．1986．

［6］ORDELL D E．Forced duty cycling of air conditioning units for load management［J］．IEEE Transactions on Power Systems，1987，2（4）：1110-1116．

［7］N P．E T W，BENENSON P．Technology assessment report duty cycling controllers revisited［R］．the US：US Department of Energy，1998．

［8］辛洁晴，吴亮．商务楼中央空调周期性暂停分档控制策略［J］．电力系统自动化，2013，37（5）：49-54．XIN Jieqing，WU Liang.Duty cycling control of air conditioners in business buildings［J］.Automation of Electric Power Systems，2013，37（5）：49-54（in Chinese）．

［9］ALOUANI A T.A new estimate of a heater/air conditioner duty cycle based on themaximum likelihood theory［C］//Power Symposium，1990，Proceedings of the Twenty-Second Annual North American.IEEE，1990：136-144.

［10］YUAN X，NIE H，SU A，et al.An improved binary particle swarm optimization for unit commitment problem［J］.收稿日期：2015-08-03。

Expert Systems with Applications，2009，36（4）：8049-8055.

（编辑徐花荣）

Study on the Optimal Duty Cycling Control Period of Air Conditioning

GUAN Guobing1，WANG Zhicheng2，XIN Jieqing1，HE Jin1
（1.Shanghai Jiaotong University Key Laboratory of Control of Power Transmission and Conversion，Ministry of Education，Shanghai 200240，China；2.Jinshan Electricity Supply Company，SMEPC，Shanghai 201500，China）

In view of the problem that the existing duty cycling control（DCC）period of air conditioning is not verified theoretically，this paper presents the demonstration model of the optimal period for duty cycling control（DCC）.It minimizes the hourly average load of air conditioning during the control period and researches the change of the optimal control period of DCC from the aspects of average outdoor temperature，allowed room temperature fluctuation range and equivalent thermal parameters in the numerical example.The results show that the optimal control period of DCC should only include the forced shutdown period and the sustained cooling period.Therefore，for the specific area，the allowed room temperature fluctuation range and equivalent thermal parameters are the decisive factors of the control cycle for DCC.The larger the room temperature fluctuation range，heat capacity of users' refrigeration space or thermal resistance of building envelope，the larger the control period of DCC.

air conditioning control；duty cycling control；optimal control period；ETP model；thermal comfort

1674-3814（2015）12-0031-05

TM925.12

A

管国兵（1990—），男，硕士研究生，研究方向为智能用电管理；

王志成（1983—），男，工程师，研究方向为电力营销；

辛洁晴（1973—），女，副教授，博士，研究方向为电力营销、电力市场、配网规划；

何津（1992—），男，硕士研究生，研究方向为电力系统及其自动化。

国家自然科学基金重点项目（51337005）。

Project Supported by the National Natural Science Foundation of China（51337005）.