水轮发电机气隙不均匀对磁场强度及转子磁极应力变化的影响分析
2015-10-26马晨原彭金宁翟鹏庞宏强闵江涛
马晨原,彭金宁,翟鹏,庞宏强,闵江涛
(西安热工研究院有限公司,陕西西安 710054)
水轮发电机气隙不均匀对磁场强度及转子磁极应力变化的影响分析
马晨原,彭金宁,翟鹏,庞宏强,闵江涛
(西安热工研究院有限公司,陕西西安710054)
定子内腔和转子外圆气隙不均匀是大型水轮发电机组的主要振源之一。在定子和转子间产生的不均衡磁拉力,对转子和定子形成转频激扰力。为探讨气隙不均匀与磁场强度及电磁应力之间关系,依据发电机的实际结构,考虑铁心饱和的情况,以局部电磁力计算方法中的局部麦克斯韦应力法和虚位移法为基础,结合有限元软件电磁模块分析工具,对水轮发电机转子对中及偏心的6种工况进行发电机内部整体气隙磁场磁感强度及转子表面应力分析,研究水轮发电机气隙变化对转子磁极应力的影响。
水轮发电机;偏心;气隙磁场;应力分析;有限元法
水轮发电机气隙不均匀,将对转子产生单边不平衡磁拉力。这种不平衡磁拉力作用于转子轴系,将引起机组振摆数值超标,对机组稳定运行产生隐患。发电机转子气隙变化将导致转子表面的应力集中,如果磁极的应力达到一定程度将使其变形,单纯依靠监测振动信号是无法检测的。这可能威胁到机组的安全运行,严重的将导致发电机扫膛等重大事故。因此,准确计算和分析大型水轮发电机组在不同工况下气隙磁场强度及磁极应力分布情况,是目前大型机组设计和电磁激振研究的重要课题[1]。
气隙不均匀对水轮发电机的危害主要在于:发电机气隙发生畸变,进而导致发电机转子受力不均匀,属于磁结构耦合范畴,近年来涉及的文献不多[2]。多年来许多学者针对发电机磁场问题进行过研究,对于发电机气隙磁场研究的经典公式法的主要思想为:通过气隙磁导密度,推导出气隙磁场能量表达式,再进一步得到电磁应力与磁场强度和磁场能量的关系表达式。Belmans[3]等提出把气隙磁导展开为Fourier级数的形式并以此来调整磁动势进而推导出不平衡磁拉力的更准确的解析表达式。郭丹等把气隙磁导展开为Fourier级数的形式,通过转子或定子表面的Maxwell应力积分得到更精确的非线性不平衡磁拉力的解析表达式。根据不平衡磁拉力与转子偏心的非线性函数关系,通过简化的各向同性的单圆盘转子系统,建立了水轮发电机转子电磁振动的非线性系统,最终通过永磁系统模拟,得到了解析式。公式法计算繁琐,缺乏对整个气隙磁场变化和单个磁极的应力分析。
本文以某电站水轮发电机为例,采用有限元方法建立实体模型并计算分析,提取了发电机气隙磁场分布情况,进一步探讨转子不同偏心度与气隙磁场畸变程度及磁极应力的变化关系。
1 发电机转子偏心对气隙磁场的影响
发电机不同于一般的旋转机械,定子、转子通过气隙磁场耦合,形成了3个中心:定子中心(也可简单地认为定子铁芯中心)、转子中心(也称为转子几何中心)、转子旋转中心(由机组导轴承的位置确定)。发电机运行过程中,由于种种原因,当3个中心不重合时,机组将产生由于机械,电磁等原因的耦合振动问题[7]。磁感应强度B是表征发电机气隙的一个重要参数,假定发电机定子固定,单纯发电机转子偏心,且运行到任意位置如图1所示。

图1 转子偏心示意图Fig.1 Rotor eccentricity schematic
根据经典公式法,可以推导出任意瞬时转定子径向差为:
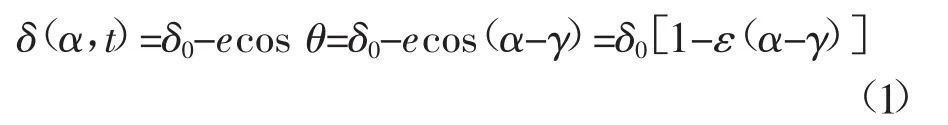
式中:δ为定、转子间的气隙偏心大小;μ0为空气的导磁系数;Kμ为饱和系数;μ1由曲线拟合计算而得,单位面积气隙磁导线性部分径向磁场强度表达式为:
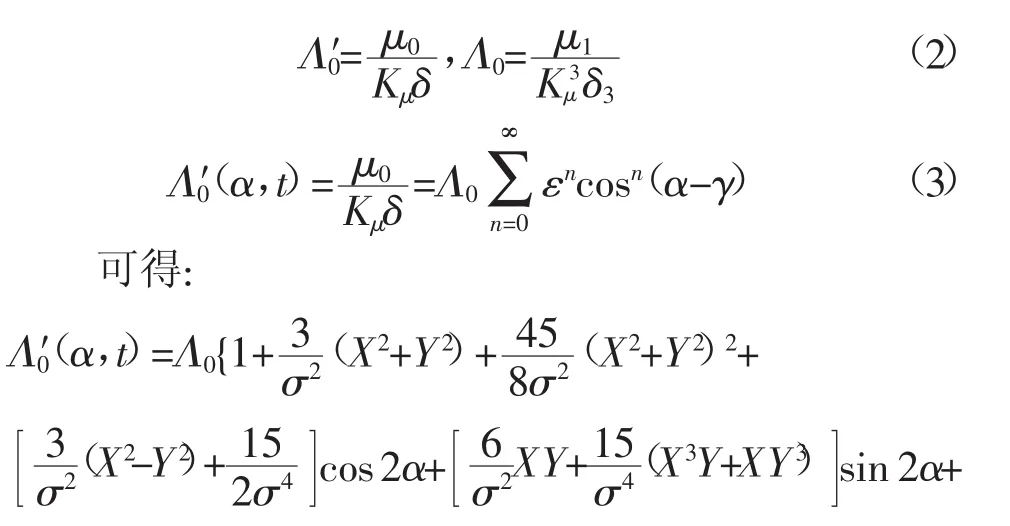
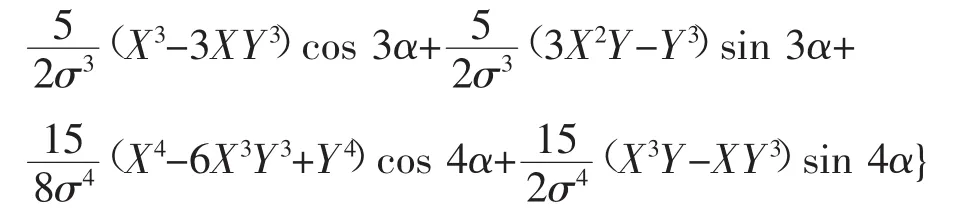
采用公式计算法分析作用于转子的电磁力,需先通过气隙磁势和磁导,求得气隙磁密[8]:
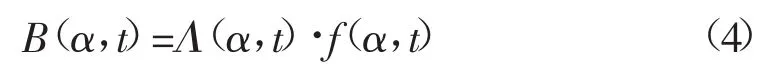
得到单位面积磁通密度:
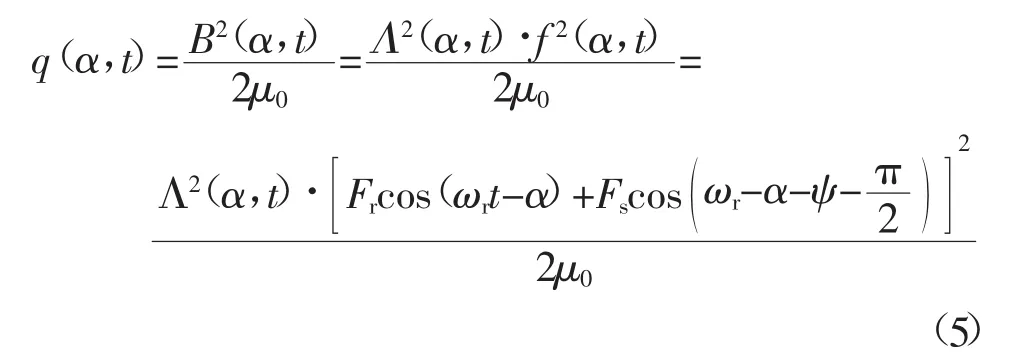
其中:μ0为空气磁导率,该公式适用于P=2的同步发电机。由式(5)可以看出,磁极应力与主极磁动势、电枢反应磁动势以及气隙磁导率等参数有关。
2 发电机模型的建立
2.1定子接线图划分
对发电机的研究,尤其对其内部受力和磁场分布的研究的基础是加载发电机内部电流。本文计算的对象为某电站的水轮发电机,该发电机为三相多极同步发电机,发电机额定功率200 MW定子90槽,磁极为12对,气隙对中状态下最小值为2.5 cm,发电机转子半径为6 m,定子Y型接线,额定电压3.6 kV,额定电流In=60 A,频率f1=50 Hz,额定功率因数cos φ= 0.8(滞后),直轴同步电抗Xd=70 Ω,交轴同步电抗Xq=50 Ω,不计定子阻抗,及压圈和拉杆构成的鼠笼对空载磁场的影响,额定工况运行。计算三相绕组的定子接线图主要参数,每相槽数q计算公式为:

式中:Z为槽数;P为极对数;m为相数。根据该水电站参数计算得:
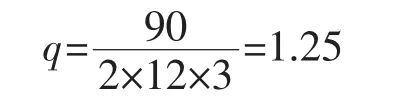
根据划分定子接线方式选择“三相单层分数槽绕组”型式,其中A相展开图如图2所示。
2.2有限元模型的建立
有限元模型需建立由转子支架、转子磁极、定子硅钢片、定子线棒、气隙等组成的耦合模型。定子硅钢片B-H曲线如图3所示。
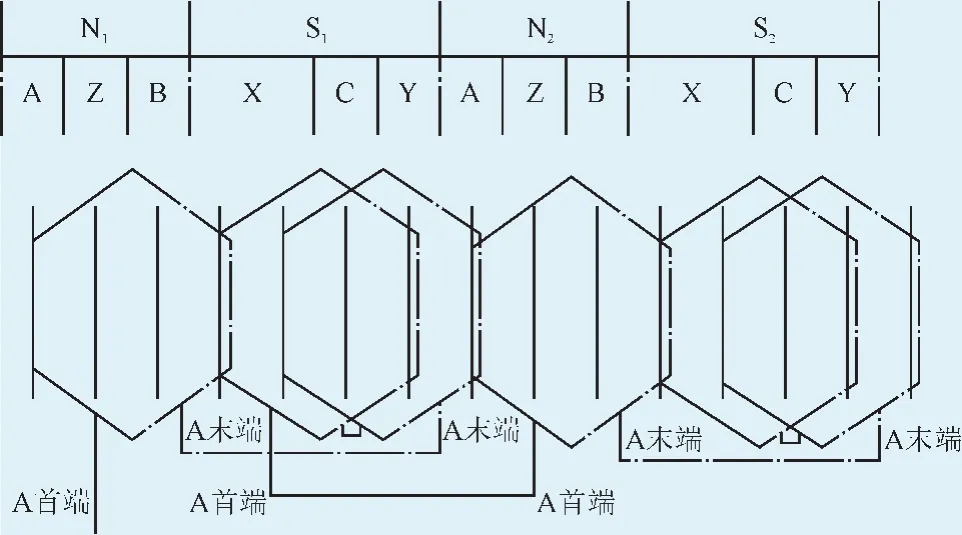
图2 定子三相单层分数槽绕组A相展开图Fig.2 Phase A expansion view of the three-phase single-layer fractional slot winding

图3 定子硅钢片B-H曲线图Fig.3 B-H curve of the stator silicon steel
由于气隙是发电机进行能量交换的重要媒介,磁极线圈及定子线棒添加电流载荷,因此网格数取自由划分的2级。其余部分为硅钢片,主要作用为形成磁路,故网格数取自由划分的5级。建立模型后进行叠分操作,并给定材料属性。将转子整体定义为一个体,约束定子外围所有节点,设置平行条件。由于发电机转、定子磁场均以同步转速进行旋转,即假定发电机向某一极方向偏心,该转子磁极的径向受力不随发电机旋转而改变。依次给定定子电流密度以后,采用电磁模块的静态分析求解器进行求解。

图4 发电机网格剖分及磁极积分路径方向规定图Fig.4 Generator meshing and integral path diagram
本文定义1号磁极朝向为+X方向,7号磁极朝向为-Y方向。分别讨论转子对中及+X方向偏心10%e、偏心20%e、偏心30%e、偏心40%e、偏心50%e,共6种工况进行研究。
3 气隙磁感强度的提取及磁极应力分布的计算
3.1气隙磁感强度与转子偏心度的关系
转子偏心将导致圆周气隙不均匀,这直接影响磁感应强度的变化。大部分电厂引入了以监测气隙距离为原理的检测设备,而磁感应强度的大小及应力分布没有涉及。后处理器中应用PATH模块定义路径,本文通过定义以定子中心为圆心,半径为6.02 m的气隙圆,将BSUM映射到路径上,得出气隙磁感分布曲线图。依次对转子不同偏心度时发电机气隙磁感强度进行计算,整理绘制如图9所示。
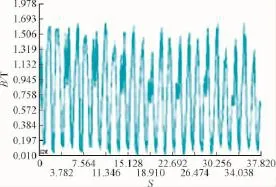
图5 转子对中状态下发电机圆周气隙Fig.5 The generator air-gap magnetic in alignment

图6 转子偏心50%e发电机圆周气隙Fig.6 The generator air-gap magnetic of the rotor of 50%eccentricity
由图9中可以明显看到,发电机转子对中运行状况下气隙磁感应强度值在1.6 T的范围内稳定运行,而气隙磁感强度的变化与转子偏心度密切相关。气隙最小处的磁感强度相对于对中时增加了35.31%,而气隙最大处磁感强度相对于对中时降低了32.06%。

图7 转子对中状态下发电机气隙磁流密度Fig.7 The generator air-gap magnetic flux density with the rotor in alignment

图8 转子偏心50%e状态下发电机气隙磁流密度Fig.8 The generator air-gap magnetic flux density with the rotor of 50%eccentricity
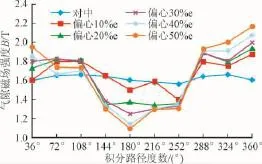
图9 不同偏心状态下发电机气隙磁感分布图Fig.9 The generator air-gap magnetic distribution of different eccentricities
3.2转子应力的分布变化
为研究清楚发电机偏心状态运行的各磁极应力大小,分别取1号及7号磁极进行分析,磁极积分路径如图4所示。沿路径取一系列点,将应力值映射到路径上。FMAG表述如图10~12所示。
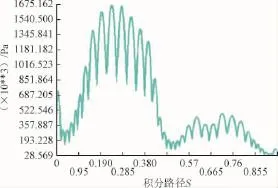
图10 转子对中状态下发电机1号磁极FMAG图Fig.10 1#pole FMAG of the rotor in alignment
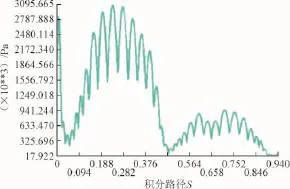
图11 发电机偏心50%e时1号磁极FMAG图Fig.11 1#pole FMAG of the rotor with 50%eccentricity

图12 不同转子偏心状态时发电机1号磁极应力分布图Fig.12 1#pole FMAG of the rotor of different eccentricities
由图比较知:图中1号磁极应力最大值从对中状态下的1.675×106Pa增加到3.95×106Pa,增幅为84.78%。相对幅值最大增长点为选点1位置,相对增加了139%。1号转子表面应力,由转子对中到转子偏心50%e情况过程中,平均值增加了71.37%。
1号极为转子偏心方向对应的转子磁极,而与偏心方向成90°的磁极受力取7号磁极进行分析。积分路径如图4所示,沿路径取一系列点,将应力值映射到路径上。FMAG表述如图13~15所示。
由图不难看出,7号磁极应力的最大值及平均值随发电机转子X方向的不同偏心度无明显变化,最大偏差为8.33%,最小偏差为0.57%,平均偏差为2.56%,基本可忽略。

图13 对中状态下发电机7号磁极FMAG图Fig.13 7#pole FMAG of the rotor in alignment
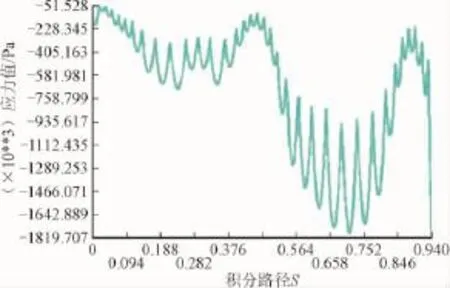
图14 发电机偏心50%e时7号磁极FMAG图Fig.14 7#pole FMAG of the rotor with 50%eccentricity

图15 不同偏心状态下发电机7号磁极应力分布图Fig.15 7#pole FMAG of the rotor of different eccentricities
由两磁极的2种工况对比知:对中状况下,1号磁极的最大应力值为1.675×106Pa,7号磁极的最大应力值为1.74×106Pa,在软件误差范围内可认为对中情况时,各磁极应力数值基本一致,圆周磁拉力对整体发电机转子无影响;偏心方向的磁极应力与偏心度成正比,而与偏心方向成90°的磁极应力与偏心度无明显关系。
4 现场实验数据
某电站扩大性大修后,通过气隙检查参数知:机组盘车状况良好,双面间隙0.2 mm,启动试验正常,空转情况良好,盘车结束后检查发电机气隙距离如表1所示。
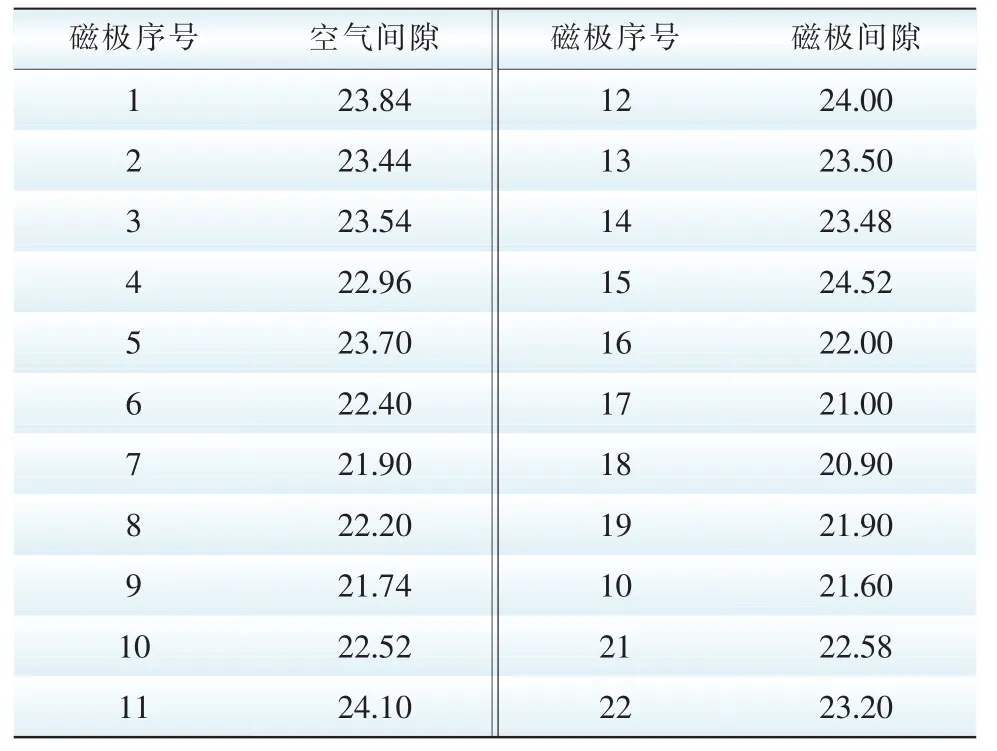
表1 发电机气隙检查表Tab.1 The list of the generator air-gap mm
气隙测量结果:最大24.10 mm,最小20.90 mm,平均间隙为22.774 mm.偏差:-8.0%~+6.0%,符合要求。
但是运行10 d后,发现运行过程中发电机定子振动较大并伴随尖锐刺耳的噪音,在线监测系统监测气隙+X方向和-Y方向发生振动超标现象,Y方向摆度增加50%,气隙监测两个方向的气隙间距有明显波动变化,如图16所示。
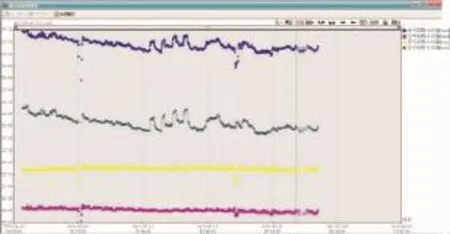
图16 机组运行气隙检测图Fig.16 The air gap detection with the unit in operation
停机检查,发现定子铁芯松动,气隙发生变化,最小值达到15.5 mm。气隙不均匀使发电机受到不平衡磁拉力影响,经排查检修后重新打紧定子定位螺栓,收紧上导瓦,问题得到解决。上导最大摆度从28.9×10-2mm下降到9.8×10-2mm,机组运行状态良好,机组机械运行参数如表2所示。
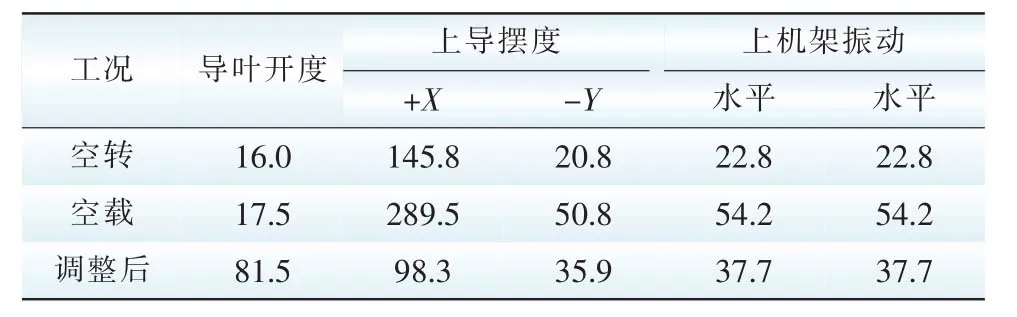
表2 消缺前后机组振摆位移对比表Tab.2 Vibration displacement comparison table before and after eliminating defects 10-3mm
5 结论
发电机内部磁场和磁极应力分布情况一直是研究的难点,由于其内部磁场分部复杂和动力性因素,所以本文挑选了比较有针对性的1号和7号转子磁极进行分析,计算并总结了偏心度与转子受力及气隙磁场的联系:
1)转子对中运行时,气隙磁场磁感应强度延圆周方向均匀分布。转子偏心运行时,发电机气隙发生变化,导致气隙磁场磁感应强度发生畸变。气隙磁感强度数值在最大处增大了35.31%,在最小处减小了32.06%。
2)本文选取发电机1号磁极正对偏心方向,其应力分布与偏心度成正比,1号磁极表面平均应力值最高增加了71.37%。
3)文选取发电机7号磁极与偏心方向成90°,其应力分布与转子偏心度无明显关系。
4)发电机气隙变化直接影响转子受力,在运行中有可能导致机组故障,危害性不容小觑,材料强度等安全问题需进一步讨论。
[1]肖孝锋.水轮发电机组气隙监测与转轮应力测试研究[D].武汉:华中科技大学,2006.
[2]张绍睿.高效谐波起动异步电动机[C]//昆明:全国火力发电厂汽轮机专业技术交流研讨会,2008.
[3]BELMANS R,VANDENPUT A,GEYSEN W.Calculation of the flux density and the unbalanced pull in two pole induction machines[J].Archiv fur Elektrotechnik,1987,70(1):151-161.
[4]邱家俊.机电分析动力学[M].北京:科学出版社,1992.
(编辑李沈)
Analysis of Impacts of the Uneven Air Gap of the Hydro-Power Generator on the Magnetic Field Strength and the Stress Variation of the Rotor Magnetic Pole
MA Chenyuan,PENG Jinning,ZHAI Peng,PANG Hongqiang,MIN Jiangtao
(Xi’an Thermal Engineering Research Institute,Xi’an 710054,Shaanxi,China)
The uneven air gap in the stator cavity and rotor outer is one of the main vibration sources of the large-sized hydro-power generator.The unbalanced magnetic pull generated between the stator and rotor forms the rotating frequency excitation force to the rotor and stator.To investigate the relationship of the uneven air gap between the magnetic force and magnetic intensity,according to the real structure of the generator,considering the saturation of the core,based on the local Maxwell stress and virtual displacement in the local electromagnetic force calculation and the electromagnetic analysis tool of the finite element software,this paper presents an analysis of the magnetic induction of the whole air gap magnetic field inside the generator and the stressed on the rotor surface in 6 different conditions of the rotor in alignment and misalignment,and studies impacts of the air gap changes on the rotor magnetic stress.
hydro-power generator;misalignment;air gap magnetic field;stresses analysis;FEM
1674-3814(2015)11-0131-06
TM312
A
2015-08-12。
马晨原(1987—),男,西安热工研究院有限公司工程师,主要从事水轮发电机组调试及振动分析研究工作。
