三相电压型PWM整流器的二自由度内模控制

朱志键，王杰

（上海交通大学电气工程系，上海　200240）

三相电压型PWM整流器的二自由度内模控制

朱志键，王杰

（上海交通大学电气工程系，上海200240）

在电压型PWM整流器的控制中，广泛采用d-q旋转坐标系下电压电流双闭环控制策略。基于传统的双闭环控制策略的不足，提出了二自由度内模控制（IMC）策略。其中电流内环基于合成矢量的思想，提出了二自由度内模解耦控制；电压外环基于功率守恒的思想，提出了扰动快速消除的二自由度内模线性控制。所提控制策略简单易于实现，既统筹考虑有功电流和无功电流综合控制并优化了PI参数整定，又实现了线性化的间接电压控制且能够快速消除扰动对系统的影响。仿真结果验证了所提方法的正确性和有效性。

PWM整流器；双闭环；二自由度内模控制；内模解耦控制；扰动快速消除；内模线性控制

随着插电式混合动力汽车的不断发展和应用，作为其充电策略的一种，能实现能量双向流动、输出电压可控、低输入电流谐波含量及功率因数接近1的三相电压型PWM整流器得到了越来越广泛的应用［1］。目前研究较多、应用最广且性能较优良的PWM整流器控制策略是采用d-q旋转坐标系下的电压电流双闭环控制策略［2］。其中电流内环控制交流侧电流的波形和相位，电压外环控制直流侧输出电压。

传统的双闭环控制策略［2］基于d-q旋转坐标系下的数学模型设计控制器。其电流内环采用前馈解耦控制方法分别控制有功电流和无功电流，并用PI控制器作为电流调节器（AIR）；电压外环用PI控制器作为电压调节器（AVR）直接把直流侧电容电压和有功电流联系起来。因而，传统的双闭环控制策略可以从以下4个方面改进和优化，分别是统筹考虑有功电流和无功电流综合控制、线性化电压外环控制、优化PI参数整定及快速消除扰动对系统的影响。文献［3］研究了三相电压型PWM整流器的L、C参数的有效范围和PI参数的整定及其对直流侧电压响应、交流侧电流谐波和功率因数的影响，提出了一套规范化的设计和参数整定方法。但整定过程复杂繁琐，难度较大，且整定所得参数还需后期调试，时间花费巨大。文献［4-6］基于合成矢量的思想统筹考虑有功电流和无功电流，将电流内环的双输入双输出模型转变为单输入单输出模型，理论简单清晰。文献［7-8］提出了利用动态过程中的无功电流来提升有功电流动态响应速度的控制策略。文献［9-11］分别基于现代控制理论中的状态反馈、自适应控制和鲁棒控制提出了一些新的控制策略。

本文基于三相电压型PWM整流器在d-q旋转坐标系下的传统双闭环控制，提出了二自由度内模控制策略。其中电流内环基于合成矢量的思想，提出了二自由度内模解耦控制；电压外环基于功率守恒的思想，提出了快速消去扰动的二自由度内模线性控制。所提控制策略简单易于实现，既统筹考虑有功电流和无功电流综合控制并优化了PI参数整定，又实现了线性化的间接电压控制且能够快速消除扰动对系统的影响。仿真结果验证了所提方法的正确性和有效性。

1　三相电压型PWM整流器的通用模型

图1是三相电压型PWM整流器通用模型的拓扑结构图。其中，esa、esb和esc为交流侧三相电压；ua、ub和uc为整流桥三相控制电压；isa、isb和isc为交流侧三相电流；ic和iL分别为电容电流和负载电流。规定图示方向为其正方向。

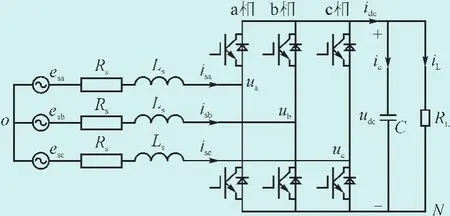
图1　三相电压型PWM整流器的拓扑Fig.1　Topology of three-phase voltage-source PWM rectifier

图中：Rs为功率开关管的等效损耗电阻R和交流侧滤波电感的等效电阻Rl之和的等效电阻；Ls为交流侧电感；RL为负载电阻；C为直流电容。

为了分析方便，首先定义开关函数sk为：

式中：k=a，b，c。根据开关函数sk的定义，可知ukN= udcsk，k=a，b，c。

假设三相交流线路完全对称，基于基尔霍夫电压定律可以建立三相静止坐标系下三相电压型PWM整流器的精确数学模型。如式（2）所示。

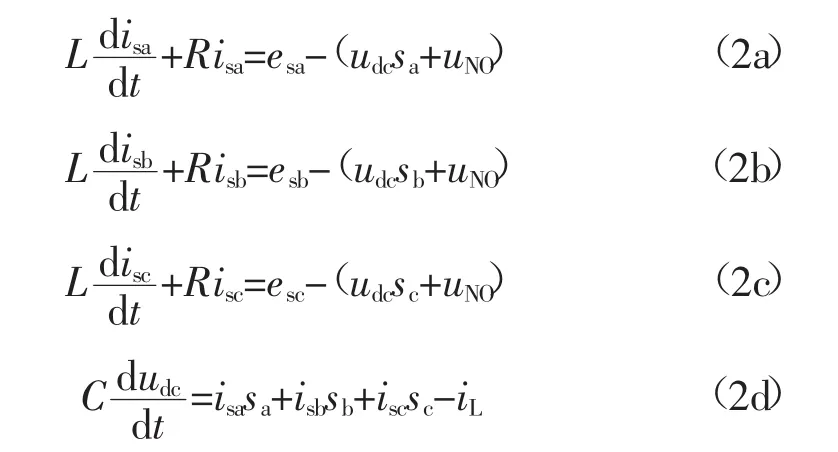
由三相电压型PWM整流电路的对称性可得：

在三相静止坐标系下采用开关函数描述的数学模型是对三相电压型PWM整流器的精确描述。但由于其交流侧均为时变交流量且开关过程存在高频分量，因此传统的PI控制器无法实现无稳态误差跟踪控制。

为了将交流侧各时变交流量变为直流量，最常见的方法是采用经典Park变换把三相静止坐标系变换为与电网基波频率同步旋转的d-q坐标系。式（4）即为变换后的同步旋转d-q坐标系下的数学模型。

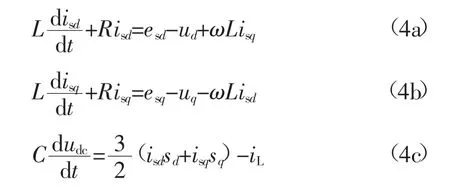
式中：sd和sq为三相开关函数相对应的d-q坐标系下的开关函数。

2　二自由度内模控制

2.1内模控制的原理

内模控制（internal model control，IMC）是一种新型控制策略，它基于过程数学模型来设计控制器。典型的内模控制（IMC）结构如图2所示。

图2　IMC结构框图Fig.2　Control block of IMC

图2中：G（s）、Gˆ（s）、C（s）分别为被控过程、被控过程的数学模型和内模控制器；u（t）、y（t）和yˆ（t）分别为输入、输出和模型输出；r（t）、d（t）和e（t）分别为参考信号、干扰信号和误差信号。为了把被控过程和控制器分开，先将图2等价变换为图3所示的经典反馈控制形式。

图3　IMC等效反馈控制系统结构Fig.3　Equivalent feedback control block of IMC

由图3可知系统的闭环响应为：

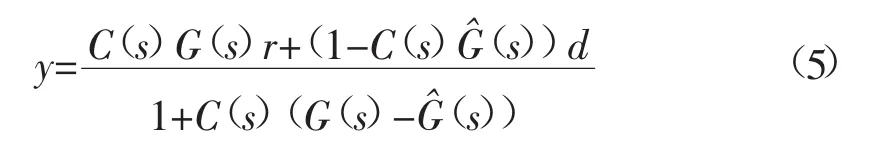
步骤二：IMC控制器的设计

在IMC控制器的设计中，为了增加系统的稳定性和鲁棒性，需要在最小相位系统的逆上增加低通滤波器。为此，定义IMC控制器为

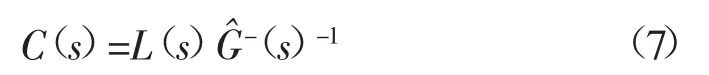
式中：L（s）低通滤波器，通常选用以下形式：

式中：α为低通滤波器的带宽，它是内模控制器需要设计的唯一参数；n为低通滤波器的阶数，选取原则为使C（s）成为有理传递函数，一般大于但最好等于G（s）分母的次数。

特别是当G（s）如本文所研究的模型不包含滞后和不稳定零点部分且为一阶系统时，有：

此时的F（s）相当于一个PI控制器，而此PI控制器需要设计的唯一参数只有α，此即为一自由度IMC。可见，优化了PI控制器的参数整定。

2.2二自由度IMC

由2.1节可知，一自由度IMC理论清晰，设计简单易行，但其不能快速地消除扰动对系统的影响。并且被控过程中存在耦合时，一自由度IMC往往不能满足系统的要求。为此，一般采用二自由度（twodegrees-of-freedom，IMC），即通过状态反馈引入第二个自由度［13］。此自由度既可用于解耦又可引入主动阻尼以增加系统对扰动的快速消除能力［14］。

因此，二自由度IMC是指在过程控制G（s）中存在交叉耦合项或干扰项时，先通过状态反馈K（s）引入解耦项和主动阻尼项，再设计内模控制系统F（s）。如图4所示，其中K（s）是解耦项和主动阻尼项的等效。

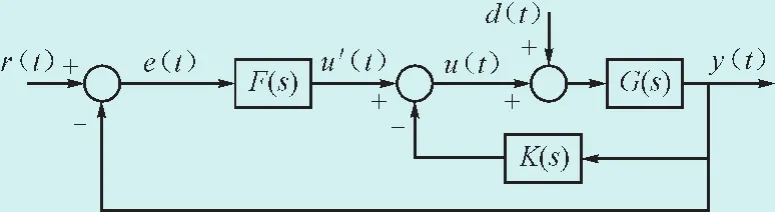
图4　二自由度IMCFig.4　Two-degrees-of-freedom IMC

3　控制策略

3.1电流环二自由度内模解耦控制

传统上，电流环一般采用前馈解耦控制策略，具体参见文献［2，13，15］，本文不再赘述。

文献［15-16］通过设计电流内环PI控制器参数实现不需要直接使用电感L准确值的解耦控制，所得电流内环控制器和文献［4-6］相同。但在解耦的彻底实现中，文献［4-6，15-16］中PI控制器参数的设计仍需电感L的准确值。鉴于实际情况下主电路参数与所检测参数之间总会存在误差，本文在假设所有主电路参数检测值和实际值相同的前提下，提出了一种基于合成矢量的二自由度内模解耦控制。

为方便起见，令：

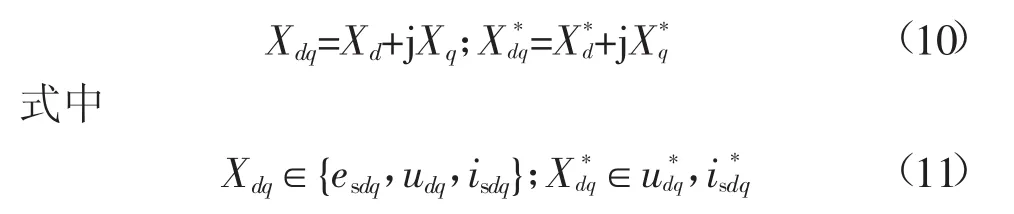
结合式（4）与式（10）有

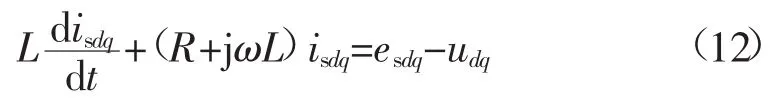
将esdq看作干扰信号，则从udq到isdq的被控过程传递函数GI（s）为

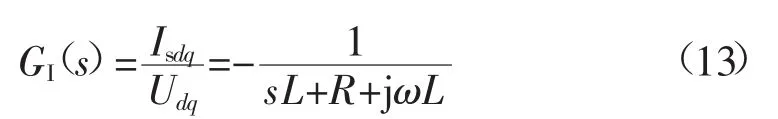
由式（13）可知，被控过程中包含耦合项jωL。根据图4知解耦项即为jωL。在电流环中一般不考虑反馈系统的主动阻尼项［14］，即因此基于合成矢量的二自由度内模解耦控制框图如图5所示。

图5　电流环二自由度内模解耦控制Fig.5　Decoupling control block with two-degrees-offreedom IMC of current loop

同样的，把esdq看作干扰信号，当时，则从u′dq到isdq的被控过程传递函数G′I（s）为

式（14）是式（9）所示的特殊情况，则有：

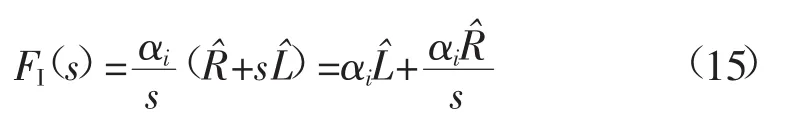
由式（15）可得PI控制器的参数为：

根据文献［12］，电流内环中的带宽应小于采样频率ωs的1/10，即有：

3.2电压环二自由度内模线性控制

由d-q坐标系下的数学模型式（4）可知，电压外环模型中具有2个典型的非线性特性变量isdsd和isqsq，传统的电压外环用PI控制器把直流侧电容电压和有功电流联系起来，并没有考虑模型的线性化。本文在充分考虑模型线性化的基础上提出了基于功率守恒的二自由度内模线性控制。

忽略等效电阻Rs所引起的损耗，则三相交流侧输出的有功功率Pac和直流侧的有功损耗Pdc相平衡，即有Pac=Pdc。

采用经典Park变换后同步旋转d-q坐标系下的有功功率和无功功率表达式为：

直流侧有功功率为

联立式（18）和式（19），有：

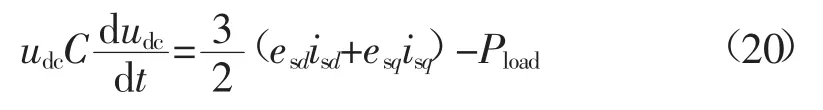
把交流侧电网电压合成矢量方向定向于d轴的方向，则q轴方向电压分量esq为0，并令W=u2dc，有：

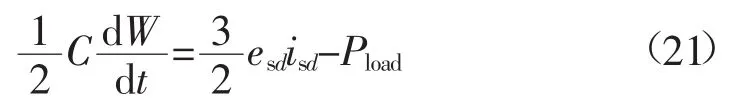
把Pload当干扰，则isd到W的传递函数GV（s）为

由式（22）可知被控过程G（s）中存在单个零极点，因此为使系统临界稳定，需通过状态反馈引入主动阻尼（极点配置）。图6中的Ga即是引入的主动阻尼项。

图6　引入主动阻尼电压外环控制框图Fig.6　Control block of voltage loop with active damping

根据图6和式（21）有：

由式（23）并根据式（9）有

由式（24）可得电压环PI控制器的参数为：

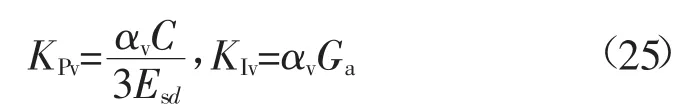
根据文献［15］，电压外环的带宽应小于等于电流内环带宽αi的1/10，即：

鉴于三相电压型PWM整流器常运行于单位功率因数，即q轴参考电流为0，则可建立如图7所示的双闭环控制框图。

图7　双闭环控制框图Fig.7　Control block of the double closed loop

4　仿真与分析

为了验证所提出的二自由度内模控制策略的正确性和可行性，本文在MATLAB/SIMULINK下搭建了仿真平台。仿真所采用的三相电压型PWM整流器的参数如表1所示。

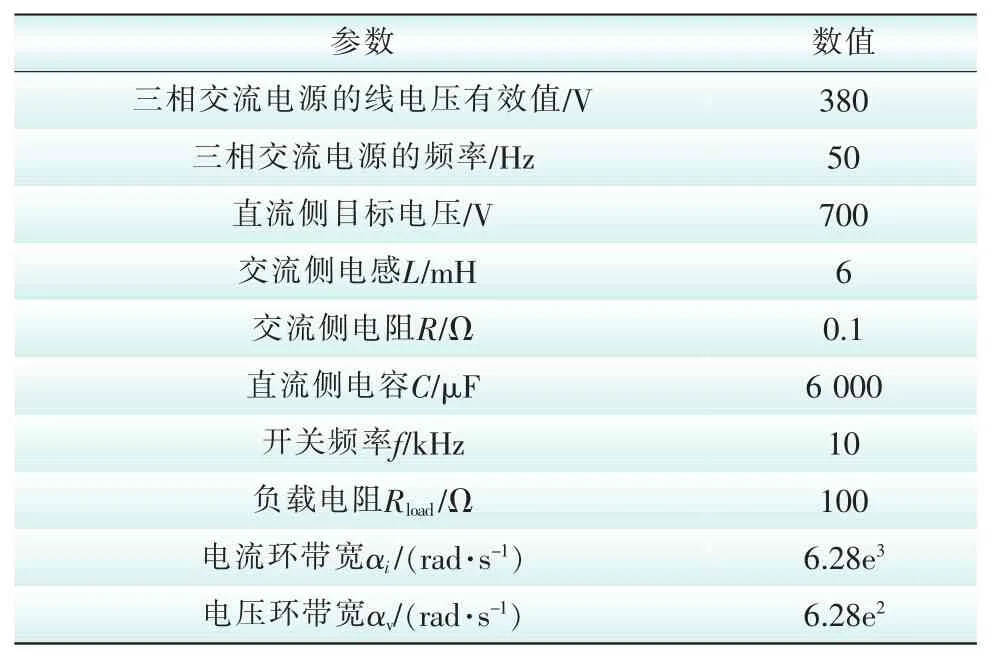
表1　三相电压型PWM整流器的相关参数Tab.1　Parameters adopted in three-phase VSPWM rectifier

为使电压环的内环和外环拥有相同响应速度［14］，一般配置G′V（s）的极点为－αv，此时KPv=Ga。如图8所示，此时电压响应渐近稳定，调节时间过长；配置极点－0.1αv时，电压响应超调大，调节时间长；配置极点为－0.01αv时，电压响应几乎无超调，调节时间短，具有良好的稳态和动态特性；配置极点为－0.001αv时，电压响应出现明显超调。因此，本文选取的配置极点为－0.01αv。

稳态仿真结果如图9所示，其中图9（a）为A相输入电压（10%）和输入电流波形图，图中输出电流和输入电压几乎完全同步，功率因数接近1。图9（b）对应直流侧输出电压波形，输出直流电压几乎没有超调，调节时间短，0.05 s时即稳定于给定值700 V，因而具有良好的稳态性能和动态性能。图9（c）为无功电流波形，其值在零参考值附近震荡，振幅小于1，表明其平均无功功率为0，即功率因数为1。

图8　配置不同极点所对应的直流侧电容电压Fig.8　Dc-link voltage of different pole assignment

图9　三相PWM整流器稳态波形Fig.9　Waveform of three-phase PWM in steady state

扰动快速消除能力对比仿真结果如图10所示。0.12 s电压参考值由700 V变为750 V；0.2 s负载由100 Ω变为50 Ω。仿真结果表明，与传统控制器相比，本文所提新型控制器在参考电压变化所引起的扰动中既能保证电流均匀不过冲，又能使直流侧电压快速响应至新的参考电压，且超调小，调节时间短；在负载扰动的情况下，传统控制器电压先减小，然后缓慢变为参考值，而新型控制器更能保证负载变化时直流侧电压不变且电流更加均匀。

图10　扰动快速消除能力对比Fig.10　The comparison of rapid elimination of disturbance

5　结语

本文在详细分析三相电压型PWM整流器的数学模型及其传统双闭环控制方法的基础上，提出了二自由度内模控制策略。其中电流内环基于合成矢量的思想，提出了二自由度内模解耦控制；电压外环基于功率守恒的思想，提出了扰动快速消除的二自由度内模线性控制。所提控制策略简单易于实现，既统筹考虑有功电流和无功电流综合控制，并优化了PI参数整定，又实现了线性化的间接电压控制，还能够快速消除扰动对系统的影响。仿真结果验证了所提方法的正确性和有效性，具有较大的工程实用价值。

［1］邓向阳，晁勤，袁铁江，等.三相联网逆变器电流控制策略研究［J］.电网与清洁能源，2011，27（5）：31-35.DENG Xiangyang，CHAO Qin，YUAN Tiejiang，et al.Current control strategies for three-phase grid-connected inverters［J］.Power System and Clean Energy，2011，27（5）：31-35（in Chinese）.

［2］宗芝荣，赵艳雷，胡希同，等.PWM逆变器的建模与双环控制策略［J］.电网与清洁能源，2009，25（11）：53-57.ZONG Zhirong，ZHAO Yanlei，HU Xitong，et al.Power inverter modeling and double cycle conthol strategy［J］.Power System and Clean Energy，2009，25（11）：53-57（in Chinese）.

［3］汪万伟，尹华杰，管霖.双闭环矢量控制的电压型PWM整流器参数整定［J］.电工技术学报，2010，25（2）：67-72.WANG Wanwei，YIN Huajie，GUAN Lin.Parameter setting for double closed-loop vector control of voltage source PWM rectifier［J］.Transactions of China Electrotechnical Society，2010，25（2）：67-72（in Chinese）.

［4］YIN B，ORUGANTI R，PANDA S K，et al.A simple single input-single-output（SISO）model for a three-phase PWM rectifier［J］.IEEE Trans on Power Electronics，2009，24（3）：620-631.

［5］陈耀军，钟炎平.基于合成矢量的电压型PWM整流器电流控制研究［J］.中国电机工程学报，2006，26（2）：143-148.CHEN Yaojun，ZHONG Yanping.Study on the current control for voltage-source PWM rectifier using complex vectors［J］.Proceedings of the CSEE，2006，26（2）：52-56（in Chinese）.

［6］BRIZ F，DEGNER M W，LORENZ R D.Analysis and design of current regulators using complex vectors［J］.IEEE Trans on Industrial Applications，2000，36（3）：817-825.

［7］钟炎平，沈颂华.PWM整流器的一种快速电流控制方法［J］.中国电机工程学报，2005，25（12）：52-56.ZHONG Yanping，SHEN Songhua.A fast current control scheme for PWM rectifier［J］.Proceedings of the CSEE，2005，25（12）：52-56（in Chinese）.

［8］CHOI J W，SUL S K.Fast current controller in threephase AC/DC boost converter using dq axis crosscoupling［J］.IEEE Trans on Power Electronics，1998，13（1）：179-185.

［9］邓卫华，张波，丘东元，等.三相电压型PWM整流器状态反馈精确线性化解耦控制研究［J］.中国电机工程学报，2005，25（7）：97-103.DENG Weihua，ZHANG Bo，QIU Dongyuan，et al.The research of decoupled state variable feedback linearization control method of three-phase voltage source PWM rectifier［J］.Proceedings of the CSEE，2005，25（7）：97-103（in Chinese）.

［10］周鑫，郭源博，张晓华，等.基于自适应跟踪控制的三相电压型PWM整流器［J］.中国电机工程学报，2010，30（27）：76-82.ZHOU Xin，GUO Yuanbo，ZHANG Xiaohua，et al.Threephase voltage-type PWM rectifier based on adaptive tracking control［J］.Proceedings of the CSEE，2010，30（27）：76-82（in Chinese）.

［11］TAN G，ZHANG H，QIAN M，et al.Optimization of three-phase PWM rectifier robust control system based on improved PSO algorithm［J］.Intelligent Automation&Soft Computing，2011，17（7）：847-858.

［12］HARNEFORS L，NEE H P.Model-based current control［13］张崇巍，张兴.PWM整流器及其控制［M］.北京：机械工业出版社，2003：112-123.

of AC machines using the internal model control method［J］.IEEE Trans on Industrial Applications，1998，34（1）：133-141.

［14］OTTERSTEN R.On control of back-to-back converters and sensorlessinduction machine drives［M］.Sweden：Chalmers University of Technology，2003：83-96.

［15］王恩德，黄声华.三相电压型PWM整流的新型双闭环控制策略［J］.中国电机工程学报，2012，32（15）：24-30.WANG Ende，HUANG Shenghua.A novel double closed loops control of the three-phase voltage-sourced PWM rectifier［J］.Proceedings of the CSEE，2012，32（15）：24-30（in Chinese）.

［16］WANG E，HUANG S.A control strategy of three-phase voltage-sourced PWM rectifier［C］//Electrical Machines and Systems（ICEMS），2011 International Conference on，Wuhan，China：IEEE，2011：1-5.

（编辑冯露）

Two-Degrees-of-Freedom Internal Model Control of the Three-Phase Voltage-Sourced PWM Rectifier

ZHU Zhijian，WANG Jie
（Department of Electrical Engineering，Shanghai Jiaotong University，Shanghai 200240，China）

The double closed loop control strategy in the d-q synchronous frame is a widely adopted control strategy of the three-phase voltage-sourced PWM rectifier.Based on the insufficiency of the traditional control strategy，this paper proposes two-degrees-of-freedom internal model control（IMC）strategy，which is composed of a decoupling control of inner current loop with two-degrees-of-freedom IMC based on the idea of resultant vector and disturbance fast-rejection linear control of outer voltage loop with two-degrees-of-freedom IMC based on the idea of power conservation.The proposed control strategy is simple and easy to implement.Using this proposed strategy can not only realize the overall consideration of active and reactive current and optimization of parameter tuning of PI controllers，but also achieve the linearized control of the voltage loop and fast rejection of the impacts caused by disturbance.The simulation results demonstrate the validity of the proposed control method and the feasibility of the control strategy.

PWM rectifier；double closed loops；twodegrees-of-freedom internal model control（IMC）；decoupling control with IMC；disturbance fast-rejection；linear control with IMC

1674-3814（2015）11-0001-06

TM46

A

2015-06-19。

朱志键（1991—），男，硕士研究生，电力系统稳定与控制设计，灵活交流输电系统分析与控制；

王杰（1960—），男，教授，博士生导师，研究方向为复杂系统非线性控制、自适应控制、鲁棒控制、电力系统非线性控制与稳定分析。

国家自然科学基金项目（61374155）。

Project Supported by National Natural Science Foundation of China（NSFC）（61374155）.