电网水电站群短期优化调度模型体系及应用分析

唐海华，张世钦，黄春雷，陆涛，沈笛

（1.南京南瑞集团公司水利水电技术分公司，江苏南京　211106；2.国网福建电力调度控制中心，福建福州　350003）

电网水电站群短期优化调度模型体系及应用分析

唐海华1，张世钦2，黄春雷1，陆涛1，沈笛1

（1.南京南瑞集团公司水利水电技术分公司，江苏南京211106；2.国网福建电力调度控制中心，福建福州350003）

立足电网水电站群短期优化调度的业务特点及应用需求，提出电网水电系统短期优化调度的多模型转化机制及其运用准则，为水电站群的日计划方案编制提供决策支撑；以水电能源的高效利用和电力系统的电力电量平衡为基础，建立了相互关联的短期优化模型体系，重点阐述了电网水电站群可用水量与水电负荷需求的协调关系。国网直调水电系统的计算结果表明，多模型转化机制能准确体现电网的不同调度意图，并获得对应的水电站群负荷控制策略。

电网水电系统；短期优化调度；多模型转化机制；电力电量平衡

电网水电系统短期优化调度涉及的因素复杂多变，其模型理论及优化算法的研究成果颇多［1-3］。水电站群短期调度研究通常针对“以水定电”和“以电定水”分别建模，鲜于考虑其内在关联。文献［4-5］首次综合考虑了水电总负荷和可用水量，提出了水电系统短期负荷优化分配的一般性准则；文献［6］在固定可用水量优化梯级总电量时，首次将负荷典型作为约束，增强了优化结果的实用性；文献［7］则将日负荷曲线转化为约束，在给定可用水量追求发电量尽可能多时，满足水电系统总出力过程与电力负荷曲线过程的残差最小；文献［8］分别构建了无法满足电网负荷要求下得短期发电效益最大模型、给定电力负荷图及期末控制水位的调峰电量最大模型以及水电负荷平衡情况下的短期耗水能量最小模型，但模型之间缺乏理论联系。综上，现有调度模型虽在一定程度上考虑了电网水电系统的优化协调，但优化目标相对单一，无法适应水电站群调度目标的多样化需求。本文在前述研究基础上，构建了融合两种模式、兼顾多重调度目标的一体化短期优化调度模型体系，各调度模型之间具有灵活的转化机制，可有效协调水电能源高效利用与系统电力电量平衡的双边应用需求。

1　短期优化调度模型体系

1.1模型目标的客观需求

结合电网水电调度的节能增效原则及负荷平衡需求，电网水电系统短期优化调度模型构建时，其目标函数应能反映以下3方面的客观要求：

1）水电系统需承担的负荷过程与水电站群的可用水量。前者取决于电网负荷需求和其他电源的供电能力，后者则取决于水电站群中长期调度运行方式及来水情况。二者通常是矛盾的，需科学决策库蓄电能充足时的空间分配问题与不足时的协调控制策略。

2）水电系统可用电能与电网的调峰要求。丰水期水量充足，一方面水电系统受电网调峰要求，有可能强制弃水调峰；另一方面又由于低水头导致容量受阻，有可能被迫压电。

3）电力系统中“先火后水”与“先水后火”两种负荷分配方式。前者主要体现在枯水期，水电系统主要用于平衡扣除火电及其他电源后的剩余负荷，其运行方式取决于系统负荷图；后者则主要体现在丰水期，首先根据可用水量确定水电系统的负荷过程，同时考虑电网调峰需求，使水电站群承担一定的调峰任务。

1.2目标函数

为全面体现电网水电调度的客观规律，增强负荷分配的灵活性，在充分利用水能资源的前提下，充分发挥水电的调节优势，本文构建了包含四元目标函数群的短期优化调度模型体系。

模型Ⅰ：能量协调均衡。给定水电系统应承担的负荷图及目标电站群可用水量，使目标电站群在可用水量不足时增加的耗能比例尽可能均衡，或可用水量过剩时增加的蓄能比例尽可能均衡，数学描述如下：

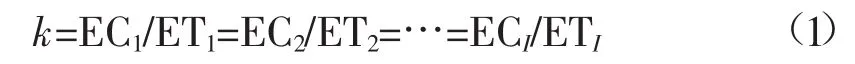
式中：I为目标电站的数目；k为能量协调比例；ECi、ETi（i=1，2，…，I）分别为i电站的协调能量（可用水量不足为耗能增量，过剩则为蓄能增量）与控制耗能量（调度期的入库电能与库蓄电能之差）。

模型Ⅱ：基荷增量最大。当汛期水量丰沛，且受汛限水位严格控制，剩余水量不可留蓄时，应在满足电网调峰要求前提下，尽量承担基荷电能：

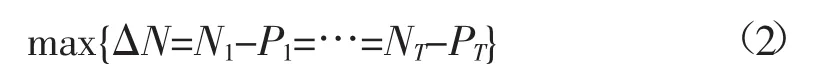
式中：T为调度期总时段数；Nt、Pt（t=1，2，…，T）分别为t时段水电系统总出力及应承担的最小负荷（取决于调峰需求）；ΔN为水电系统多承担的基荷。

模型Ⅲ：峰荷损失最大。水电系统可用水量不满足负荷需求且水量不可超用时，尽可能稳定基荷，按“削平头”方式最大程度压峰荷：

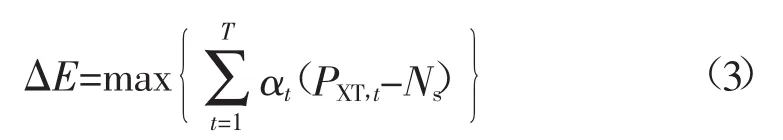
式中：ΔE为水电系统少承担的峰荷；PXT，t为t时段水电系统需承担的负荷，即水电负荷需求；Ns为水电系统实际承担的最大负荷；αt为系数，当PXT，t≤Ns时αt= 0；反之，αt=1。

模型Ⅳ：基荷损失最小。水电系统可用水量不满足负荷需求且水量不可超用时，使压基荷损失最小：

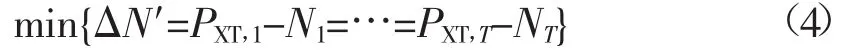
式中：ΔN′为水电系统少承担的基荷，且ΔN′＞0。

1.3约束条件

1）水电系统功率平衡约束：

式中：Ni，t为i电站t时段的平均出力。

2）各水电站水库水量平衡约束：

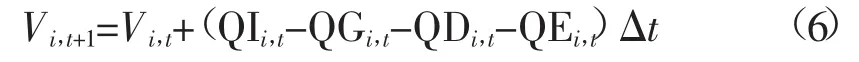
式中：QIi，t、QGi，t、QDi，t、QEi，t分别为i电站t时段的入库流量、发电流量、弃水流量及其他出库流量（包括航运、灌溉、供水、流量损失等综合利用需求）；Vi，t、Vi，t+1分别为i电站t时段初、末蓄水量。

3）各水电站水库可用水量约束：

式中：Zi0、Ziend分别为i电站调度期初始水位与期末控制水位，反映了库蓄水量变化，其差值与入库来水叠加即为可用水量。

4）梯级流量传播约束：

式中：Ωi，up为i电站入库径流依赖的上级水电站序号集合；ICi，t为i电站t时段的区间入库流量；Qi，j为i电站依赖的上级水电站群出库流量过程。

5）各水电站水库库容约束：

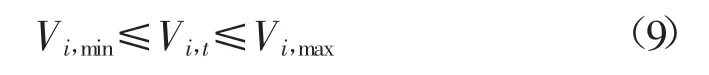
式中：Vi，min、Vi，max分别为i电站调度期内的蓄水量下限与上限。

6）各水电站水库出库流量约束：

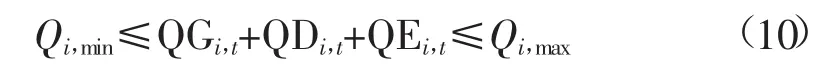
式中：Qi，min、Qi，max分别为i电站调度期期内的出库流量下限与上限。

7）各水电站平均出力约束：

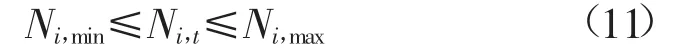
式中：Ni，min、Ni，max分别为i电站调度期期内的出力下限与上限。

8）各水电站机组单机出力约束：

式中：NEi，l，t为i电站l机组t时段出力；Ωi，l为i电站l机组振动区或气蚀区。

9）水电站静态特性及机组发电约束：

式中：Zi，up，t为i电站t时刻坝上水位；Zi，down，t、Hi，t分别为i电站t时段平均下游水位、净水头；fZV，i（·）、fQZ，i（·）、fNQ，i，l（·）分别为i电站库容曲线、下游水位流量关系及l机组的特性曲线。

10）典型负荷等比例约束：

式中：NTYi，t为i电站t时段典型负荷值。

1.4模型应用准则及目标转化机制

本文建立的水电站群短期优化调度模型体系较为全面的反映了水电系统短期调度的客观需求，给定总可用水量体现了水电站群的中长期调度控制策略，给定水电系统负荷图则体现了电网的电力电量平衡需求。模型Ⅰ给出了水电站群在可用水量与负荷图双重约束下，库蓄电能增加或减少的协调原则，体现了公平调度思想，具有双重含义，调度意图转换灵活，给定水量有余可均匀留蓄，给定水量不足则可均匀超用库蓄水能，亦可转化为模型Ⅲ或模型Ⅳ压负荷，调度人员视电网需求灵活选择；模型Ⅱ反映了丰水期电力系统的“先水后火”负荷分配方式，目标函数值大小同时取决于调峰要求及水电系统的可用容量；模型Ⅲ与模型Ⅳ均体现了水电系统可用水量或可用容量不足时的负荷分配方式，以不改变目标电站总水量为前提，分别采用不同的压电方式减少系统负荷，无调峰需求时，按峰荷损失最大“削平头”，反之则可采用基荷损失最小的“均匀压电”方式缓解电网调峰压力。

综上，调度模型群可分为2类：能量协调均衡属于给定水电系统负荷，优化水电站群的实际用水量；另外3个目标则是固定水电站群可用水量，优化水电系统负荷过程。该模型体系下各优化目标彼此之间密切关联，结合电网不同时期的电站来水特点及系统负荷需求，各模型优化目标之间存在如图1所示的相互转化机制。

图1中：方向1代表站群电能有余；方向2代表库蓄水量不能超用；方向3代表站群来水及容量富余；方向4代表电能充足但容量不足；方向5代表无调峰需求；方向6代表调峰形势紧张。

2　模型求解关键技术

上述模型的目标函数群及约束条件构成了一个多元、高维、多阶段、多约束的超大型非线性规划极值问题，本文采用双层控制法进行求解：上层控制4个目标函数之间的转换，协调下层模型的负荷和可用水量双重约束；下层则寻求给定目标函数与约束条件的最优解。下层优化由于同时受可用水量和负荷的双重限制，可能造成模型无解，因此，需选取负荷平衡电站，松弛其期末水位控制约束，以确保系统负荷得以满足。优化策略不满足模型约束的程度反映在负荷平衡电站调度期末库蓄水量与其控制值的差别上。要使这一差别满足精度要求，需靠上层模型进行调控。算法结构见图2。

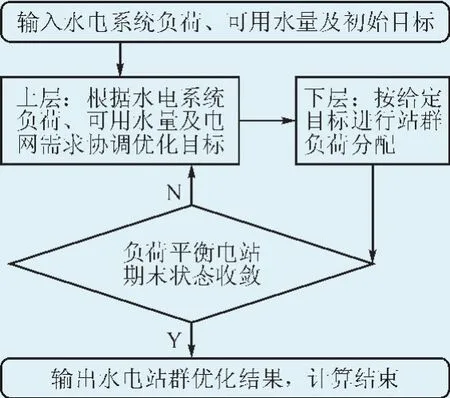
图2　模型求解双层算法结构示意图Fig.2　Double algorithm structure of solving the model

根据图2的分层协调思想，本文模型可按如下步骤求解：

步骤1：确定负荷平衡电站，其负荷调整尽可能不影响其他电站入库径流，并具备较好调节能力；

步骤2：非负荷平衡电站根据可用水量按典型负荷等比例分配方式计算出力决策；

步骤3：由水电系统总负荷扣除上述出力决策得负荷平衡电站出力决策；

步骤4：计算负荷平衡电站期末状态，判断其是否满足精度要求，若不满足，则根据电网需求协调上层目标，返回步骤2，直至负荷平衡电站的调度期末状态收敛，计算结束。

3　应用实例

目前，国网直调水电系统包括三峡、溪洛渡、向家坝、锦西、锦东、官地等大型水电站群，分布于长江中游干流、金沙江下游和雅砻江下游等梯级，具有装机容量大、发电水头高、综合耗水率低等特点。水电站群水力拓扑关系见图3，基础特性参数及计算边界见表1。

以某汛后枯水日为例，选择三峡作为负荷平衡电站，水电系统总负荷及各电站的典型负荷过程（不同时段间的负荷比例关系，表征调峰起止时间和相对调峰深度）见图4。由于官地至溪洛渡、向家坝至三峡的传播时间均超过了日计划调度周期，溪洛渡和三峡应视为龙头电站，不考虑上游传播影响，因此，表1中锦西、溪洛渡和三峡为入库流量，其余则为区间流量。另，锦东为引水电站，调节库容小，其典型负荷与锦西完全一致。按不同优化模型计算的统计结果见表2和表3，对应的水电系统总负荷过程见图5。

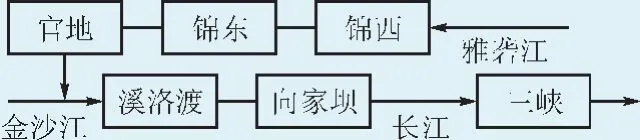
图3　水电站群水力拓扑关系Fig.3　Topological relationship of the hydropower station group

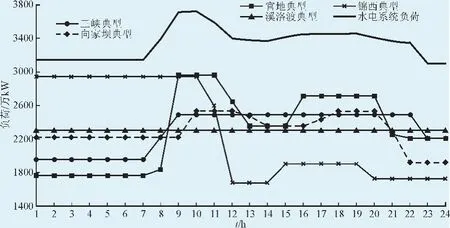
图4　水电系统负荷与电站典型负荷过程Fig.4　Process of hydropower system load and hydropower station typical load

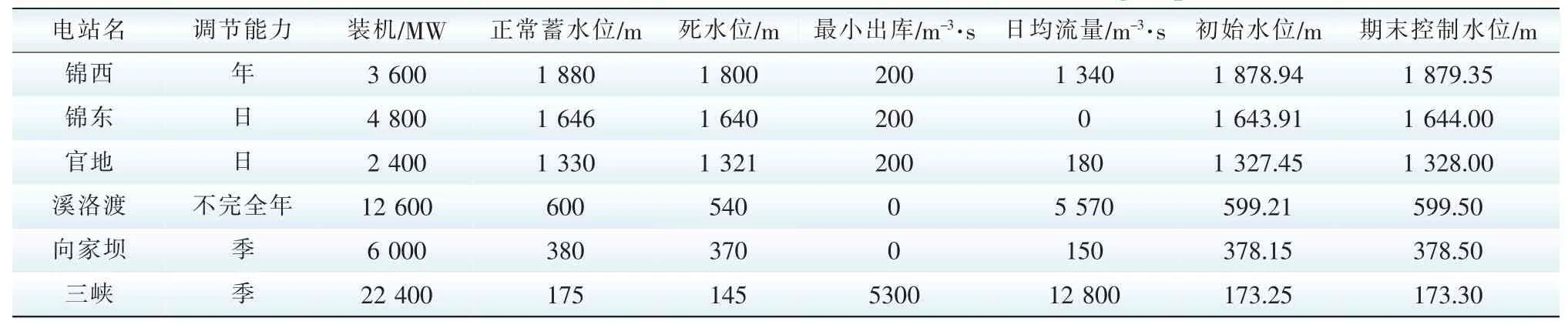
表1　水电站群计算参数表Tab.1　Calculation parameters of the hydropower station group

表2　模型Ⅰ计算结果统计Tab.2　Calculation result statistics of ModelⅠ

表3　模型Ⅲ和模型Ⅳ计算结果统计Tab.3　Calculation result statistics of ModelⅢand ModelⅣ

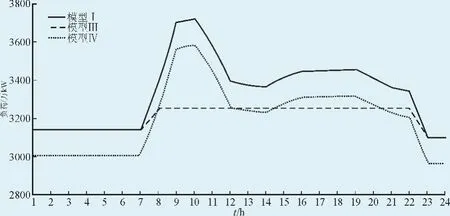
图5　不同优化模型计算所得水电系统负荷过程Fig.5　Process of hydropower system load with different optimization models

表2中，模型Ⅰ因水电系统承担调峰任务，负荷需求不可调整，水电站群的期末控制水位均无法满足，共超用水量8 668.74万m3，总耗能增加2 976.53万kW·h，平均增幅为3.978%。理论上，根据能量协调均衡原则，各电站的能量协调比例应完全相等。本例中，因锦东调节库容较小，期末已超用至死水位，实际耗能增幅仅为3.95%，其余各电站多承担了部分调节任务，耗能增幅均为3.98%。

若可用水量不能超用，此时需转化为模型Ⅲ或模型Ⅳ。当水电系统调峰形势紧张时，应采用模型Ⅳ均匀压基荷；反之，则可转为模型Ⅲ逐级压峰荷。

由表3可知，模型Ⅲ因水量不足导致的电量差为3 116万kW·h，峰荷差达471万kW；模型Ⅳ均匀压基荷135万kW，对应电量差为3 240万kW·h，比模型Ⅲ多损失124万kW·h。图5直观反映了固定可用水量后，按不同优化模型进行转换的水电系统负荷过程对照关系，其中模型Ⅰ为水电系统的实际负荷需求，模型Ⅲ和模型Ⅳ分别体现了“削平头”与“均匀压电”两种调整方式下的负荷变化。

综上，模型Ⅰ固定负荷过程，普遍存在水量超用现象，实际耗能增大；固定可用水量后，转化为模型Ⅳ的调峰效果最为理想，模型Ⅲ则水电负荷过渡更为平稳。

4　结语

本文建立了电网水电系统的短期优化调度模型体系，构成了水电站群在电网调度中的通用模型框架。现有优化模型群基本实现了电网水电调度意图的灵活转化，但仅考虑了水电系统可用水量与负荷需求之间的协调，未来还可结合火电、风电、光伏、核电等多元电源的联合调度需求横向扩充优化模型，进一步丰富和深化电网水电系统的调度任务及其多模型转化内涵。

［1］谢红胜，吴相林，陈阳，等．梯级水电站短期优化调度研究［J］．水力发电学报，2008，27（6）：1-7.XIE Hongsheng，WU Xianglin，CHEN Yang，et al.Research on short-term optimization operation of cascade hydropower stations［J］.Journal of Hydroelectric Engineering，2008，27（6）：1-7（in Chinese）.

［2］王金文，范习辉，张勇传，等．大规模水电系统短期调峰电量最大模型及其求解［J］．电力系统自动化，2003，27（15）：29-34.WANG Jinwen，FAN Xihui，ZHANG Yongchuan，et al.Short-term generation scheduling for the peak-energy maximization of large-scale hydropower systems［J］.Automation of Electric Power Systems，2003，27（15）：29-34（in Chinese）.

［3］龙军，秦雅．基于模糊理论和遗传算法的梯级水电站短期优化调度［J］．广西大学学报：自然科学版，2011，36（2）：314-319.LONG Jun，QIN Ya.Short-term optimization scheduling of cascaded hydro-plant reservoirs based on fuzzy and genetic algorithm［J］.Journal of Guangxi University：Nat Sci Ed，2011，36（2）：314-319（in Chinese）.

［4］陈森林，万俊，刘子龙，等．水电系统短期优化调度的一般性准则（1）［J］．武汉水利电力大学学报，1999（3）：34-37.CHEN Senlin，WAN Jun，LIU Zilong，et al.The general principle of short-term optimization dispatching in hydroelectric system（1）［J］.Wuhan Univ of Hydr&Elec Eng 1999（3）：34-37（in Chinese）.

［5］陈森林，万俊，刘子龙，等．流域水电站群短期优化调度的均匀用水最小模型［J］．水电能源科学，1999，17（3）：9-12.［6］唐海华，陈森林，赵宇.三峡梯级电站短期优化调度模型及算法［J］.水电能源科学，2008，26（3）：133-136.TANG Haihua，CHEN Senlin，ZHAO Yu.Model and algorithm of short-term optimal scheduling［J］.Water Resources and Power，2008，26（3）：133-136（in Chinese）.

CHEN Senlin，WAN Jun，LIU Zilong，et al.Uniform water utilization minimum model of hydropower stations short-term optimization dispatching in a basin［J］.International Journal Hydroelectric Energy，1999，17（3）：9-12（in Chinese）.

［7］纪昌明，俞杉，张晓星，等．按日负荷图运行的梯级水电站群短期效益比较［J］．电力系统保护与控制，2011，39（14）：64-68.JI Changming，YU Shan，ZHANG Xiaoxing，et al.Shortterm operation benefit analysis of cascade reservoirs based on power load curve［J］.Power System Protection and Control，2011，39（14）：64-68（in Chinese）.

［8］赵振华，周建中，李承军.清江梯级水电站短期优化调度模型研究［J］．计算机仿真，2003，20（10）：43-45.ZHAO Zhenhua，ZHOU Jianzhong，LI Chengjun.The research of short-term optimal operation model for the cascade hydroelectric stationson Qingjiang［J］.River.Computer Simulation，2003，20（10）：43-45（in Chinese）.

（编辑李沈）

Short-Term Optimal Scheduling Model System and Its Application of Electric Grid Hydro-Power Station Group

TANG Haihua1，ZHANG Shiqin2，HUANG Chunlei1，LU Tao1，SHEN Di1
（1.Water Conservancy and Hydro-Power Technology Branch，NARI Group Corporation，Nanjing 211106，Jiangsu，China；2.State Grid Fujian Electric Power Dispatching and Control Center，Fuzhou 350003，Fujian，China）

According to the business characteristics and application requirements of the short-term optimal scheduling of the hydro-power station group in the power grid，this paper puts forward a multiple model conversion mechanism and its application in the short-term optimal scheduling of the electric grid hydro-power system.This model can provide decision supports for the daily plan scheming of the hydro-power system.Based on the efficient utilization of hydro-power energy and the balance of electric power and energy in power system，this paper builds the short-term optimization model system.It elaborates the coordination relationship of the available water and load demand of the hydro-power station group in the power grid，and the connotation of the multiple objective scheduling of the hydro-power system.The calculation results of the hydro-power system in SGCC show that，the multiple model conversion mechanism can accurately reflect different scheduling intent，and obtain the corresponding control strategy of the hydro-power station group.

electric grid hydro-power system；short-term optimal scheduling；multiple model conversion mechanism；balance of electric power and energy

1674-3814（2015）11-0126-05

TV697.1+2

A

2015-07-15。

唐海华（1982—），男，硕士，高级工程师，研究方向为水电能源优化及调度自动化。