数字图像处理课程中数学函数的形象化教学改革方法研究*

☆ 陈霄 陈玉忠邓蕾蕾刘妍

（1.吉林农业大学信息技术学院，吉林长春 130118；2.吉林大学实验室与设备管理处，吉林长春 130000；3.吉林艺术学院动漫学院吉林长春 130000）

数字图像处理课程中数学函数的形象化教学改革方法研究*

☆ 陈霄1陈玉忠2邓蕾蕾1刘妍3

（1.吉林农业大学信息技术学院，吉林长春 130118；2.吉林大学实验室与设备管理处，吉林长春 130000；3.吉林艺术学院动漫学院吉林长春 130000）

数字图像处理是一门理论与实践并重的课程，课程与数学模型紧密相关，对于本科学生的学习是一个难点。针对数学模型不易理解这一问题，本文提出一种将数学模型形象化，图像处理实例特殊化，实践课程兴趣化的教学模型。让学生在更有效地理解数学模型的同时，可以更有效地运用图像处理方法。

数字图像处理；数学模型；形象化教学

一、引言

“数字图像处理”是高等院校信息类专业的重要专业课程，也是与计算机视觉、模式识别、认知计算等研究相关的热门学科。该课程希望通过对数字图像处理基本理论的学习，建立学生对数字图像处理学科的有效认知与兴趣，通过实验课强化数字图像处理的编程能力，为学生未来就业从事图像相关领域的工作奠定基础。数字图像处理课程涉及范围广，难度大，要求学生具有良好的数学和信号处理等相关知识的基础，并且掌握一种编程语言［1，2］。同时，随着近几年计算机视觉的发展，图像处理的新方法新思路更新迅速，如何更好地开展该课程教学，如何让学生理解数字图像处理并自主研究相关领域知识一直是专业课教师思考的问题。

二、课程特点及教学现状

“数字图像处理”课程是一门理论与实践并重的课程，所涉及到的内容很丰富，课程中涉及的每个章节或每种算法都可以作为一个研究内容；该课程涉及计算机技术、数学物理、通信技术等知识，要求学生在前期学习中具有较好的相关知识基础。

传统“数字图像处理”课程的教学存在以下问题：（1）开课时间过晚，高年级学生对课程了解少，缺乏兴趣，并且对该课程不够重视。（2）以往经验认为该课程注重实践，因此加大了实验课教学环节，增加实验课实践，虽然学生得到一定程度提高，但总体学习还不够理想［3］。

根据对学生的调查，部分学生认为课程晦涩难理解，老师讲解的数学模型枯燥，不知道图像处理中理论知识部分的作用，希望能够更直接或者更实例化地讲授该门课程。而讲授课程的教师也很为难，该课程与数学理论知识紧密相连，没有这些理论知识，很难真正理解该课程精髓，如果改成完全实例化教学，那可能与本科教学的目的不相符，只有更深入地了解课程中数学模型才可以更有效地利用，因此，仅仅以工程化举例是不够的。根据这一问题，我们采用数学模型形象化，图像处理实例特殊化，实践课程兴趣化的教学模型。让学生更有效地理解数学模型的同时，可以更有效地运用图像处理方［4］。

三、改革的教学内容

1.形象化数学模型讲授方法

学生们普遍反映数学模型晦涩，公式复杂很难理解。如小波变换，傅里叶变换，Gabor变换等都是数字图像处理课程中重要的内容，也是课程的难点，这些数学变换模型复杂，学生不易理解。我们将复杂的数学变换公式转化为数学模型，以形象化的方法将数学公式展示给学生。比如：在讲解Gabor变换时，Gabor变换实质上是傅里叶变换的加窗函数，Gabor变化的定义式如下。

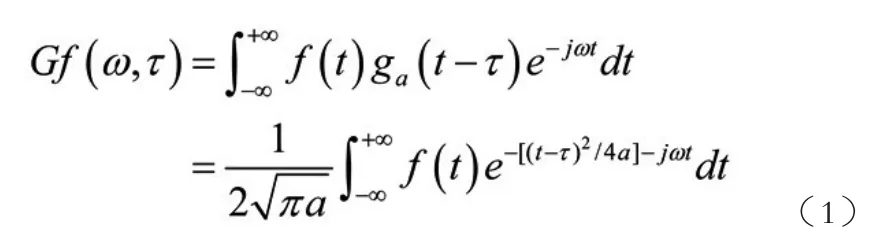
单从公式角度看，公式中参数多且难于理解，我们可以用图形化方式向学生解释什么是傅里叶变化的加窗函数。假设傅里叶函数如图1所示。

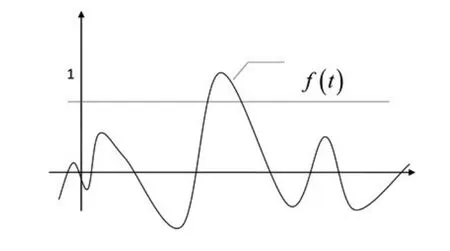
图1 傅里叶变换

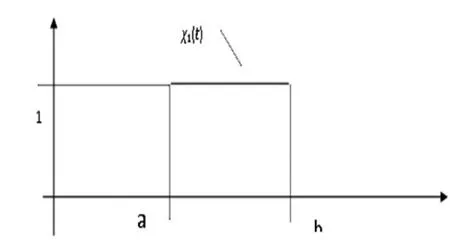
图2 窗口函数

现在只想得到f（t）函数在区间［a.b］的部分，因此可以引入窗口，（如图2）。有了傅里叶函数f（t）和窗口函数f（t），那么加窗的傅里叶函数就是两个函数的乘积，表示为G（x）=x1（t）f（t），其形象化的数学表达形式如图3所示。

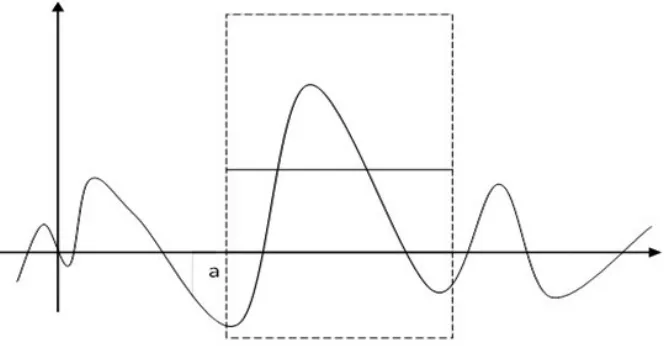
图3 G（x）函数

其中，虚线框内得到的函数就是所说的傅里叶加窗函数，这样再把窗口函数x1（t）换为高斯函数，就是我们通常所说的Gabor函数。这样讲解，学生在了解傅里叶变换和高斯变换的前提下，形象化地理解了Gabor变换。但是仅仅了解数学函数基本图像还不够，我们还要进一步让学生理解函数。

2.多参函数变换的形象化教学

函数中必定存在着数学参数，而参数调节会对函数变化产生影响，因此，讲解参数对函数变换的影响，可以进一步加深对函数的理解，同样，利用2D-Gabor函数举例。函数2D-Gabor的数学表达形式如下。

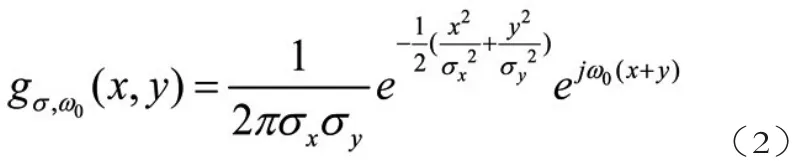
公式中参数较多，形式复杂，主要参数包括σx和σy，分别表示函数在x轴和y轴方向上的标准差，ω0表示空间频率。这样的讲解较为晦涩。我们利用形象化的数学图像解释该函数与参数间的关系。

对于二维Gabor，参数变化引起图像形状的变化，不同参数的二维Gabor，在进行图像特征提取时也会产生不同效果，针对该函数，通过调节某一参数，观察二维Gabor图像，以及特征提取结果的变化情况。二维Gabor核函数如下。

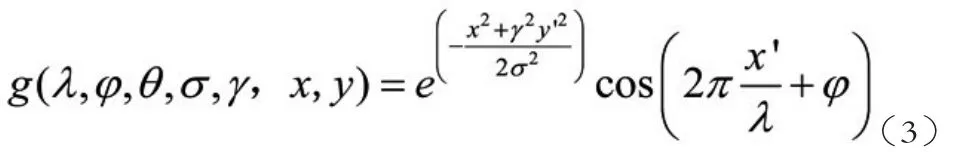
图4 参数λ对图像影响

如图4所示，图像中是波长分别为λ=5，λ=10的二维Gabor图像，其他参数的值如下：方向0，相位偏移0，长宽比0.5。

除此以外，还有方向参数θ，相位参数φ，形状参数γ，都采用通过调节参数，观察数学函数相应的变化，最终对数学函数有一个较为深入的理解。

3.特殊实例的展示

本研究根据函数特点，选取特殊实例，实例可以选取极限状态下的数字图像，以突显函数的作用，我们仍用二维Gabor函数为例，选取图5中（a）等边的八边形进行实验，此实例可以对检验二维Gabor对于纹理方向的敏感性（如图5）。

图5 2D-Gabor在不同方向的响应

图5中（a）图为实验用的等边8边形，以下使用相同波长参数λ=8，不同方向的二维Gabor对图5中（a）进行特征提取，从图（b），（c），（d）和（e）中可以看出二维Gabor对纹理方向的响应敏感，图5中（f）为θ=0°，θ=45°，θ=90°和θ=135°的四方向滤波图像结果，可以看出基本上提取了六边形的纹理，但是相对特征显得有些粗糙；图5中（g）是波长为λ=4，方向θ=0°，θ=30°，θ=60°，θ=90°，θ= 120°和θ=150°的6方向滤波特征提取结果。可以看出六边形六方向滤波处理结果要比四方向效果要细致一些。

以此种方法，给予学生特殊实例图像，启发学生进一步思考：在调节相位参数φ后数字图像处理效果会有什么变化，并作为实验课内容让学生完成，以更有效地让学生理解数学模型中参数变化对图像处理的影响。以上通过形象化的数学图像解释数学函数，通过参数调节进一步形象化理解函数本身，在选取特殊实例进一步说明数学函数的具体功能和函数对图像变换产生的作用。这样学生可以更深入理解数学函数。

4.相似数学模型的学习延伸性

在经过一轮详细讲解数学函数方法后，我们可以将此方法延伸到其他近似函数，如小波变换，K-L变换等。在学习数字图像处理课程中关于数学函数的课程时，学生要知道这样的学习思路：把复杂数学函数转化为数学图像，通过对参数调节理解数学函数，再例举特殊实例了解数学变化在数字图像处理过程中的功能作用。学生在了解此学习方法后，老师采取启发驱动式的思想，让学生主动学习。

5.以兴趣和学校特点为导向教学和实践方法

形象化的数学模型讲解大大改善了数字图像处理课程，但是兴趣往往是学生重要的老师，因此我们在教学过程中注重兴趣培养［5］。

（1）通过前沿性的图像处理技术提高学生兴趣。数字图像处理是一门前沿科学，教材课程重点介绍常用算法，使学生掌握数字图像处理原理。再结合国内外多种教材，精选本学科相关的中英文期刊，本区域特色相关的科研热点项目等其他资料构建科学合理的教学内容和课程体系。教师将自己在科研中获得的新理论、新技术、新方法、新成果及时引入到教学中，不断充实和修正教学内容。通过一些发展中的、前沿性的算法着重介绍其思路和原理，教导学生注重思维培养而非局限于具体算法，培养学生的学习能力和创新思维。

（2）选取有效的实验课内容：数字图像的实用性很强，让学生利用数字图像处理方法解决一些与生活上相关的问题，例如：对植物叶子上的叶脉特征提取，多幅图像拼接技术等来提高学生主动学习的积极性。同时，还要考虑学校科研大环境，吉林农业大学作为一个以农业为主的大学，在信息科学上也要结合农业，将数字图像处理课程设计有效结合于农业科学，以农业为导向，完成数字图像处理综合应用。

四、结束语

数字图像处理课程一直存在学生感觉难、听课兴趣不足，教师感觉累、教课不积极的问题。通过对数字图像处理课程进行形象化教学方法，以贴近生活的实例为内容，通过前瞻性的科学知识吸引学生，并结合学校科研环境，有导向地设计课程实验。促进科研的同时，更主要的是可以有效地提高学生对课程知识的掌握，促进学生对学习知识的综合应用，使学生具有更好的创新能力。

［1］张书真，宋海龙.专题化教学模式在《数字图像处理》课程中的实践［J］.现代计算机，2011，（01）：54-56.

［2］李飞鹏，胡云峰.《数字图像处理》实践教学改革与效果分析［J］.中国科技信息，2010，（20）：258-259.

［3］贾永红.数字图像处理课程的建设与教学改革［D］.武汉：武汉大学，2007.

［4］饶俊慧.数字图像处理课程教学改革探索［J］.中国科教创新导刊，2012，（10）：22-23.

［5］曹玉东，王冬霞，周军.数字图像处理课程教学改革与探索［J］.辽宁工业大学学报，2013，15（02）：129-134.

*吉林省教育科学“十二五”规划课题（GB13180）。

G434

A

1671-7503（2015）05-0045-03

郑方林］