多电极电磁流量计权重函数的仿真研究

孔令富，杜胜雪，李英伟

（燕山大学信息科学与工程学院，河北　秦皇岛　066004）

多电极电磁流量计权重函数的仿真研究

孔令富，杜胜雪，李英伟

（燕山大学信息科学与工程学院，河北秦皇岛066004）

采用有限元方法，针对三对电极电磁流量计电极在不同位置时权重函数分布情况进行数值仿真。提出2个描述权重函数分布均匀度的指标：最大偏差和整体均匀度，并在电极数目和位置不同情况下对权重函数的分布情况进行分析比较。结果表明，电磁流量计权重函数分布不仅与电极数目有关，还与电极所在的位置有关。通过合理设计电极位置，三对电极电磁流量计在权重函数分布均匀度和平均强度两方面都优于单电极对电磁流量计。

计量学；多电极电磁流量计；权重函数；有限元方法；数值仿真

1　引言

电磁流量计是一种用于导电性液体流量测量的仪表［1，2］。由于其不受温度、压力、流体密度和粘度等因素影响，且其内部光滑无阻流部件［3］，不会对流体产生阻力从而导致压力损失，因此在工业生产过程的流量测量中得到广泛应用。权重函数表示管道横截面上不同位置流速对流量计输出信号的贡献大小，权重函数均匀则各点流速贡献相同。所以，在电磁流量计的设计中，总是希望权重函数分布越均匀越好。文献［4］对求解流动横截面上权重函数的数值方法进行初步研究。文献［5］研究了非满管状态下权重函数分布情况，此时权重函数分布与管内液体充满度有关。文献［6］对外流式电磁流量计和油管之间环形区域的权重函数分布情况进行了理论推导和仿真。管道横截面上流体速度呈非轴对称分布时，采用传统单电极对电磁流量计会产生较大的测量误差［7］。而多电极电磁流量计可以从多角度多位置测量感应电动势，故可用于非轴对称管流流量的精确测量［8］。文献［9］提出了一种八电极电磁流量计，可以消除流速分布不对称对测量结果的影响。文献［10］利用弦端压差测量方法研究了不同电极数目和尺寸对平均流速估计的影响。文献［11］基于权重函数理论设计了一种多电极电磁流量计。

目前，对多电极电磁流量计权重函数分布情况的研究还较少。本文旨在研究多电极电磁流量计在管道横截面上权重函数的分布特性。研究结果可为多电极电磁流量计传感器的结构优化提供进一步研究的基础。

2　基本方程与权重函数

当导电性液体在磁场中作切割磁力线运动时，液体中有感应电流产生。根据欧姆定律有［12］：

式中：j为电流密度矢量，是通过液体单位面积的电流；σ为流体电导率；E为电场强度；V为流体速度；B为磁感应强度。

激磁电流角频率ω不大时，位移电流完全可以忽略，而只考虑传导电流，这时电流密度的散度为零，即▽·j=0。假设液体的电导率均匀且各向同性，则▽·σ=0。由（1）可得：

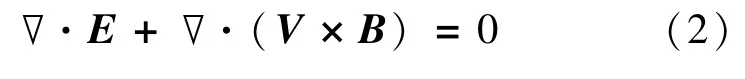
又因为E=-▽U，所以（2）可化为：

式中：U为感应电动势；▽2为拉普拉斯算子。

对均匀磁场型电磁流量计，为便于分析和阐明其物理意义，通常使用“长筒流量计”物理模型［13］。如图1所示，设磁场区域长度和电极长度均为2L，此时电极呈线状。当L→∞时，方程的求解就可由三维空间坐标问题简化成二维平面坐标问题。

图1　长筒流量计的物理模型

引入权重函数，感应电动势可表达为［7］：

式中：A为测量管容积，W为权重函数，W=▽G，G为格林函数。W是三维空间函数，Wx、Wy、Wz分别为W在坐标轴x、y、z方向上分量，对长筒流量计只考虑y方向上分量Wy。假设磁场方向平行于x轴，流速平行于z轴，则B=Bx，V=Vz。由以上条件，可得：

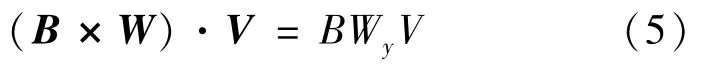
由式（5）可知，电极两端产生的感应电动势不仅与流速有关，还与权重函数分布有关。

3　权重函数的仿真与分析

3.1单电极对电磁流量计权重函数数值仿真

根据格林函数性质和电磁流量计边界条件，可得长筒流量计权重函数解析式［7］：式中r为管道内半径。由式（6）可得管道内电极所在横截面上W的分布情况，r=1时其等值线分布如图2所示。

由图2可知，在管道中心处W值为1，沿着y轴向电极M、N处移动时，W值逐渐增大；沿着x轴向管壁移动时，W值逐渐减小至0.5。权重函数越大的区域内的流体速度对电极M、N所产生感应电动势的贡献越大。由权重函数分布规律可以看出，整个测量区域内的流体速度对电极所产生感应电动势的影响程度不一样，这就解释了传统单电极对电磁流量计对流速分布的敏感性，导致其无法准确测得非轴对称流的平均流速。

采用有限元方法，使用Matlab软件中PDE工具箱，对单电极对电磁流量计在管道内电极所在横截面上权重函数分布情况进行数值仿真。在数值仿真时，关键是求解格林函数G，由于G满足拉普拉斯方程▽2G=0，假设电磁流量计边界条件如下：

具体仿真步骤如下：

（1）建立管道内电极所在横截面的几何模型；

（2）设定边界条件，采用Neumann边界条件n· （c▽u）+qu=g，式中：n为垂直于边界的单位外法向矢量。令电极M和N以外g=0，q=0，电极M处g= 1，q=0，电极N处g=-1，q=0，即可得式（7）；

（3）建立标准椭圆型偏微分方程-▽·（c▽u）+au=f，设置其系数c=1，a=0，f=0，即可得▽2u=0；

（4）对求解区域网格化，网格划分越细，精度越高，但计算量会增大；

（5）求解椭圆型偏微分方程可得u，即G；

（6）求解格林函数G在y方向上的梯度，即Wy；

（7）画出Wy的等值线分布图。

如图3所示，为权重函数数值解等值线。将其与图2进行对比，发现二者没有太大差别。表明利用有限元方法计算权重函数是高效可行的研究方法，并且可通过增加网格密度来提高计算精度。

图2　权重函数解析解等值线分布图

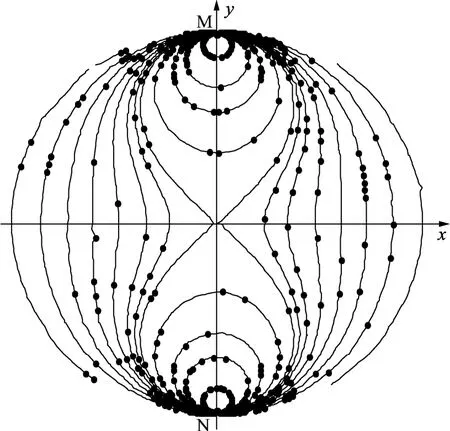
图3　权重函数数值解等值线分布图

3.2三对电极电磁流量计权重函数数值仿真

针对三对电极电磁流量计，对电极处于管道横截面上不同位置时权重函数的分布情况分别进行仿真，结果如图4所示。三对电极的位置分布如下：中间一对电极横坐标为x=0，两侧电极关于中间电极对称，它们到中间电极的横向距离为d，d的范围为0.1r～0.9r，其中r为传感器管道内半径。

3.3权重函数的数值分析

其中：W0为Wk的平均值，即。R反M应区域内权重函数的最大偏差程度；RD则反应了区域内权重函数分布的整体均匀程度，RD值越小，权重函数分布的整体均匀程度越理想。

依据上面两个指标，计算电极处于不同位置时权重函数分布均匀度，如表1所示。从图4和表1可知，权重函数分布情况不仅与电极数目有关，还与电极分布的位置有关；随着两侧电极与中间电极距离增大，权重函数的平均值W0逐渐减小，即相同流速对流量计输出信号的贡献逐渐减弱；随着两侧电极与中间电极距离增大，权重函数的最大偏差RM和RD的值都逐渐增大，权重函数的整体均匀度逐渐降低。

表1　电极在不同位置时权重函数分布情况

权重函数均匀度RD随电极位置变化趋势如图5所示。从表1和图5可知，对于三对电极电磁流量计，当中间一对电极横坐标为x=0，两侧电极到中间电极的横向距离d≤0.7r时，整体均匀度RD＜1.461 9，最大偏差RM＜10.674 6，即三对电极电磁流量计比传统单电极对电磁流量计权重函数分布的更为均匀，其管道横截面上不同位置流体速度对流量计输出信号的贡献更趋向一致，表明三对电极电磁流量计对流速分布的敏感性减弱；权重函数平均值W0＞0.085 1，表明相比单电极对电磁流量计，管道横截面上相同流速对流量计输出信号的贡献增强，即在相同条件下，三对电极电磁流量计可获得更强的感应电动势信号。

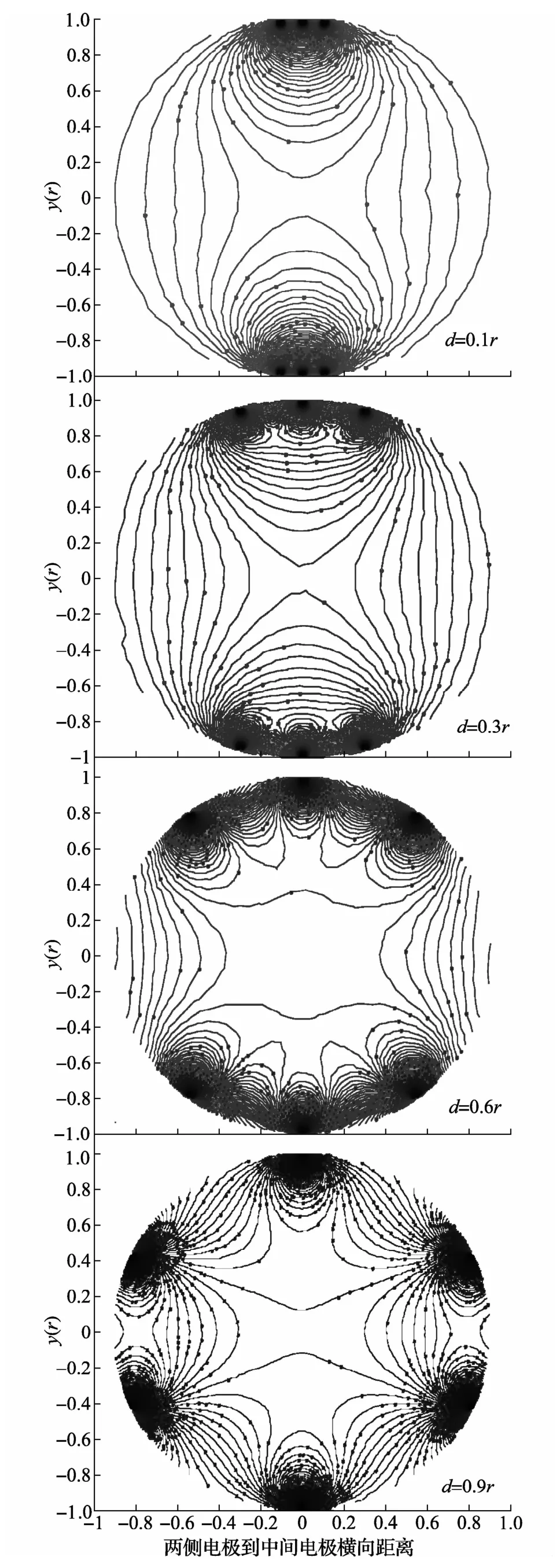
图4　三对电极位置不同时权重函数等值线分布图

图5　均匀度RD与电极位置关系图

以上针对三对电极电磁流量计权重函数分布随电极位置变化情况进行了仿真分析，研究结果为多电极电磁流量计的结构优化提供了参考依据，具有一定的理论指导意义。虽然从理论上电极数目越多，流体平均速度的测量精度越高，但从实际制作、成本和可靠性来讲，电极数目不可能无限增多，而且电极数目的增加会延长数据采集时间，导致系统实时性降低，通常只要测量精度达到要求就可以了。当然对精度有特殊要求时，可相应增加或减少电极数目。

4　结论

采用有限元方法对传统单电极对电磁流量计权重函数分布进行了数值仿真，将仿真结果与已有权重函数解析解作对比分析，验证了有限元方法求解权重函数的可行性和有效性；针对三对电极电磁流量计，电极在不同位置时，对电极所在横截面上权重函数分布情况分别进行数值仿真；定义了两个描述权重函数分布均匀度的指标：最大偏差和整体均匀度。依据这两个指标，在电极数目和位置不同情况下，分别对权重函数进行仿真分析。结果表明通过合理设计电极位置，三电极对电磁流量计在权重函数分布均匀度和平均强度两方面都优于单电极对电磁流量计。

［1］张小章，李砚涛，何涛.含有一个气泡时电磁流量计虚电流的三维特性［J］.计量学报，2002，23（3）：195-198.

［2］李曦，张小章.插入式电磁流量计的理论研究［J］.计量技术，2008，（2）：3-6.

［3］Baker R，Deacon J.The behavior of turbine，vortex and electromagnetic flowmeters［J］.The Chemical Engineer，1984，3：13-15.

［4］王经卓.电磁流量计权函数的数值仿真与验证［J］.仪器仪表学报，2009，30（1）：132-137.

［5］卫开夏，李斌.非满管电磁流量计权重函数有限元数值仿真分析［J］.自动化仪表，2012，33（9）：69-71/ 75.

［6］张志刚.外流式电磁流量计权重函数分布的仿真研究［J］.石油仪器，2010，24（1）：12-14.

［7］Shercliff J A.Thetheoryofelectromagneticflow measurement［M］.Cambridge：Cambridge University Press，1962，32-72.

［8］Horner B，MeschF，TrachtlerA.Amulti-sensor inductionflowmeterreducingerrorsdueto nonaxisymmetric flow profiles［J］.Measurement Science and Technology，1996，7：354-360.

［9］张宏建，管军，胡赤鹰.基于电磁感应原理的多电极流量测量方法［J］.计量学报，2004，25（1）：43-46.

［10］徐立军，王亚，乔旭彤，等.多对电极电磁流量计传感器电极阵列设计［J］.仪器仪表学报，2003，24（4）：335-339.

［11］赵宇洋，张涛，LUCAS G.多电极电磁流量计转换器设计［J］.传感器与微系统，2012，31（6）：87-89/93.

［12］Bevir M K.Thetheoryofinducedvoltage electromagneticflowmeter［J］.JournalofFluid Mechanics，1970，43：577-590.

［13］蔡武昌，马中元，瞿国芳.电磁流量计［M］.北京：中国石化出版社，2004，21-80.

Simulation Research on Weight Function of Multi-electrode Electromagnetic Flowmeter

KONG Ling-fu，DU Sheng-xue，LI Ying-wei
（College of Information Science and Engineering，Yanshan University，Qinhuangdao，Hebei 066004，China）

Adopting the finite element method，when the electrodes are in different positions，the numerical simulations for weight function of electromagnetic flow meter with six electrodes are carried on.Then two indexes indicating the evenness of weight function have been put forward：the maximum deviation and the overall evenness，and the distributions of weight function while the number of electrodes are different and the electrodes are in different locations are analyzed based on these indexes.The results show that weight function distribution of electromagnetic flow meter is related not only with the number of electrodes but also with position of electrodes.By reasonable designing the position of electrodes，the electromagnetic flowmeter with six electrodes is superior to dual-electrode electromagnetic flowmeter in both of the uniformity and the average strength of weighting function distribution.

Metrology；Multi-electrode electromagnetic Flowmeter；Weight function；Finite element method；Numerical simulation

TB937

A

1000-1158（2015）01-0058-05

10.3969/j.issn.1000-1158.2015.01.13

2013-04-17；

2013-07-25

国家科技重大专项（2011ZX05020-006）；河北省自然科学基金（F2014203265）；高等学校博士学科点专项科研基金（20131333110015）

孔令富（1957-），男，吉林省公主岭人，燕山大学教授，博士生导师。主要从事多相流参数测量、智能信息处理的研究。