采样间隔对分布光度计测量LED总光通量的影响
2015-10-25赵伟强杨臣铸
赵伟强,刘 慧,刘 建,2,杨臣铸
(1.中国计量科学研究院,北京 100029;2.北京师范大学,北京 100875)
采样间隔对分布光度计测量LED总光通量的影响
赵伟强1,刘 慧1,刘 建1,2,杨臣铸1
(1.中国计量科学研究院,北京100029;2.北京师范大学,北京100875)
利用计算机仿真LED单管球面空间各点照度值的方法,模拟了分布光度计标定4种典型LED单管总光通量值的过程,利用计算结果分析了分布光度计测量所采用的不同采样间隔对标定结果的系统误差。这4种LED单管的光强分布曲线分别为准朗伯、长茄形、双翼形和窄光束,涉及轴对称或非轴对称光强分布。计算结果显示,对于常见的LED单管光源,利用分布光度计采用2°等间隔法,在球带份数m值大于12的情况下,采样间隔选择所带来的系统偏差可控制在0.3%以内。
计量学;光通量;采样间隔;数学模拟;LED;分布光度计
1 引言
LED光源具有节能、环保、寿命长、体积小等特点,可以广泛应用于指示、显示、装饰、背光源、普通照明和城市景观照明等领域。LED同传统光源相比,其发光面、光束方向、光谱参数等具有特殊的多样性,因而,LED光源的检测方式不能简单套用传统的检测方式。为了提高实验室检测结果的一致性,中国计量科学研究院开展了LED光色参量计量检测的研究,并研制了相应的标准管[1~4]。本文将讨论使用分布光度计测量LED单管总光通量值时所采用的测量采样间隔选择问题,理论计算了不同采样间隔对多种类型的LED总光通量标准管的影响,为计量检测人员提供优化选择。
2 分布光度计测量总光通量的原理
分布光度计通过测量光源的空间光强分布及数值积分计算得到光源的总光通量[5]。为便于测量和计算,设被测光源处在半径为R的假想球面内,光心与球心重合,如图1所示。将球面分成n个平行的球带ΔSi(i=1,2,…,n),每一球带又分成m等分ΔSij(j=1,2,…,m)。在每一小球面ΔSij处,测量待测光源在该方向的发光强度Iij或在ΔSij上建立的照度Eij,则通过ΔSij的光通量ΔΦij为
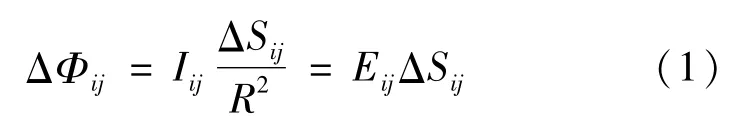

图1 球带的划分
因而光源的总光通量为

可见,测量时需对球面进行球带分割并细分。图2为球面的截面圆的示意图。该圆与球带的两底相垂直。e1,e2,…,ei为各球带与大圆的交点。上下球顶点的连线是该圆的直径。向下的方向定为0°,由各交点ei与圆心的连线和0°方向的夹角可标出各球带。球带有2种分割方法:等角度间隔法和等立体角法,前者又称为角度系数法。
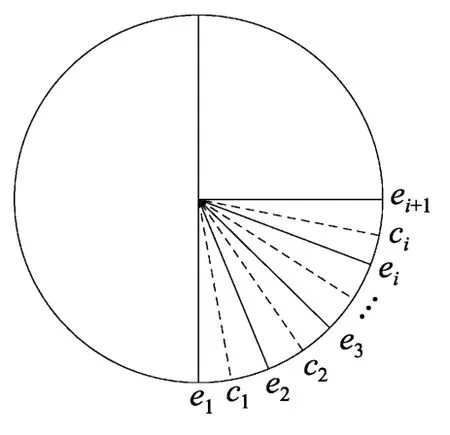
图2 球带的划分
2.1等角度间隔法
将球面按相等的角度间隔进行分割,即各球带与大圆的交点e1,e2,…,en与圆心连线之间的夹角相等。由球带公式ΔS=2π RΔh=2π R2(cos ei-cos ei+1)知球带面积不相等。在各交点ei处测量的照度近似等于附近球带上照度的平均值,则总光通量为
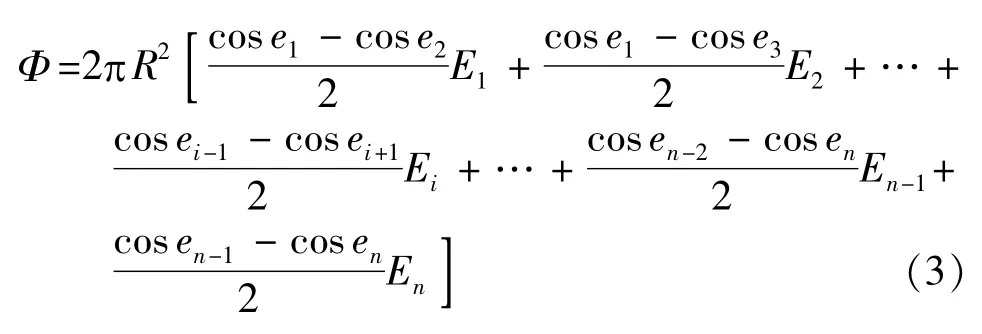
式中(cos ei-1-cos ei+1)/2称为角度系数。对于任何角度间隔,均可计算出角度系数。间隔越小,结果越准确,但测量时间越长。
2.2等立体角法
在等角度间隔法中,角度间隔相等但球带面积不相等,球带面积正比于角度系数。等立体角法则是通过将球面分割成面积相等的若干球带(即每个球带对应的立体角相等),从而避开角度系数的计算。式(1)中球带对应面积相等,仅测量出每个位置的Eij即可。
确定球带数目n以后,由球带公式有ΔS=2πR2(cosei-cosei+1)=4π R2/n,因而cos ei-cos ei+1= 2/n,考虑边界条件cose1=1,可求得球带的边界角:cosei=1-2i/n;再求出球带中间位置角度ci(见图2以及式(4)),用此处照度值近似作为平均照度。各球带等分线上方向角度通过下列公式计算:
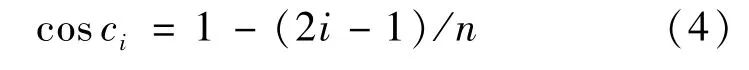
对于任何n值,均可计算出ci值。n值越大,总光通量结果越准确,但测量时间越长。
3 分布光度计的测量方式与采样间隔
从分布光度计的总光通量测量原理可知,若光源的发光强度分布曲线变化平缓,上述等角度法或等立体角法即便采用较大的间隔,仍可以获得较准确的值。LED标准单管情况与传统白炽灯不同,发光方向较后者集中。图3所示为4种常见LED发光强度分布曲线的过几何中心轴截面图[6]。
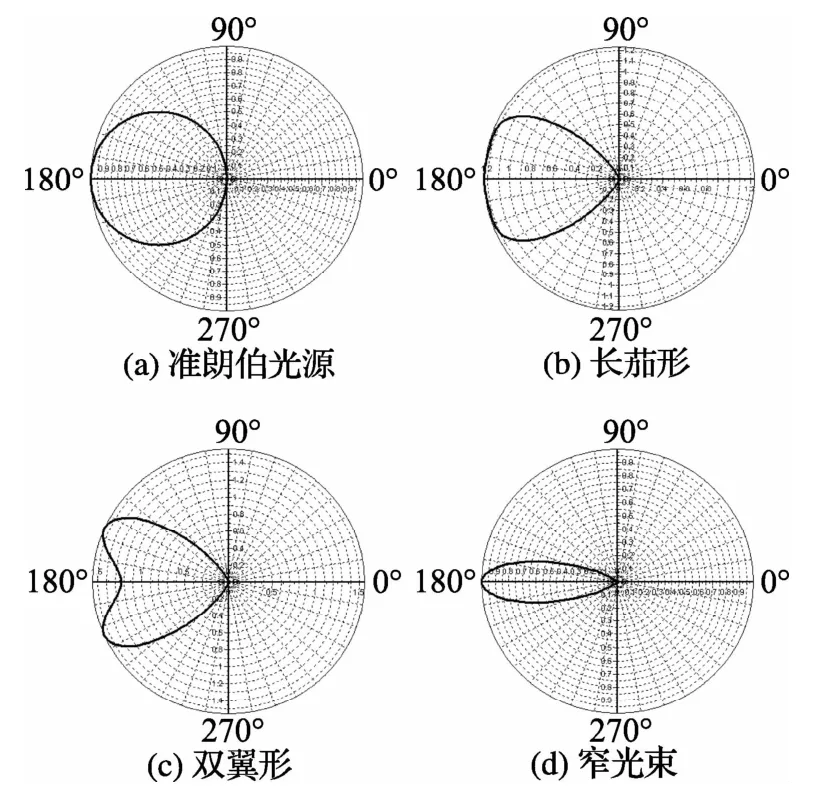
图3 4种常见的发光强度分布曲线截面
测量LED标准单管总光通量过程中,为获得较高的照度测量精度,探测器绕LED光源旋转采用步进方式,这样测量点的数量越多,测量时间更长。
4 不同采样间隔时总光通量理论计算
考虑光源的发光强度分布曲线是几何中心轴对称的情况,为简化计算,取4个函数来模拟上述典型LED标准单管截面的发光强度分布曲线,分别是

式(5)~式(8)分别对应图3(a)~图3(d),需要说明的是,上述函数只是特例,不能代表全部的LED。使用计算机程序计算上述4函数在不同采样间隔下的值与数学推导所得理想测量值的偏差,结果见表1。

表1 计算值与理想测量值的偏差(%)
计算结果显示,0.5°、1°等角度法测量4种光源因采样间隔不同带来的系统偏差小于0.05%。在测量要求高且不了解光源大概分布的情况下应采用这两种模式。若光源非窄光束分布,可适当减少采样间隔以提高测量速度,如,采用2°等角度法或50等份立体角法。5°等角度法因偏差较大,不推荐使用。
如果光源非几何中心轴对称,需对环形球带进一步细分,划分出C-γ模式中的γ角。将球带分为m等份,以窄光束分布为例进行计算,选择公式(9)来模拟发光曲线,该函数在γ角为0°和90°时的光强分布曲线见图4。

对于不同的m值,计算结果见表2。表中理想测量值是通过数值积分方法计算所得。

图4 非轴对称情况光源两垂直截面的发光强度分布曲线
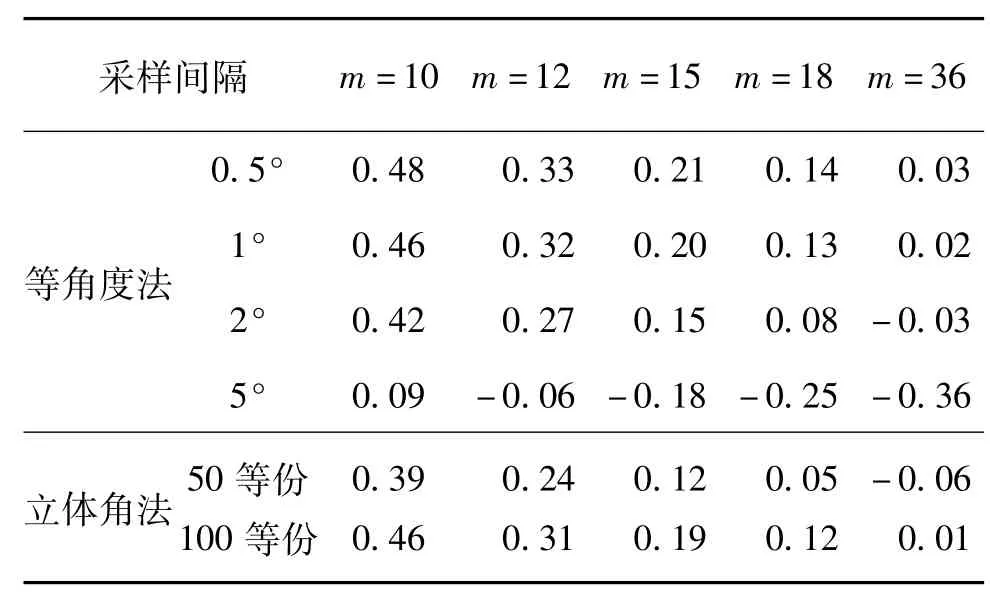
表2 m不同时计算值与理想测量值的偏差(%)
数据表明,m值对这种非轴对称情况的分布曲线影响非常明显。图5计算结果是以2°等角度法为例,计算两者之间的关系。

图5 采用2°等角度法测量结果偏差与m值的关系
随着m值的增大,偏差并非趋向于0。这归因于选用2°等角度法所存在的系统偏差。如改用0.5°等角度法计算,系统偏差将减少,见图6。

图6 采用0.5°等角度法的测量结果偏差与m值的关系
由表2、图5和图6可知,对于常见的非轴对称情况的LED单管光源采用2°等角度法,在m值大于12的情况下,系统偏差可控制在0.3%以内。而对准确率要求比较高时,建议m值大于等于18。
5 实测数据
采用中国计量科学研究院的小型LED分布光度计,对窄光束分布和准朗伯分布的LED标准管进行不同采样间隔对光通量结果影响的测试。实际测量的光强分布截面见图7及图8,测量数据见表3。
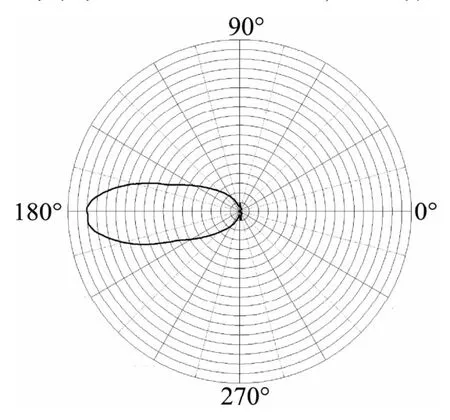
图7 实测的窄光束LED光强分布图
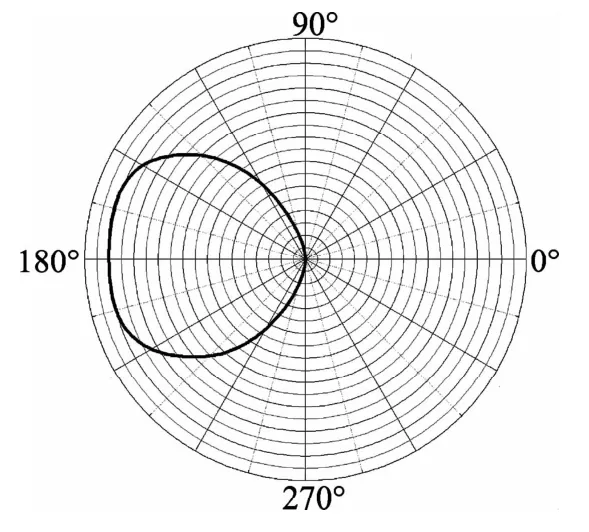
图8 实测的准朗伯LED光强分布图
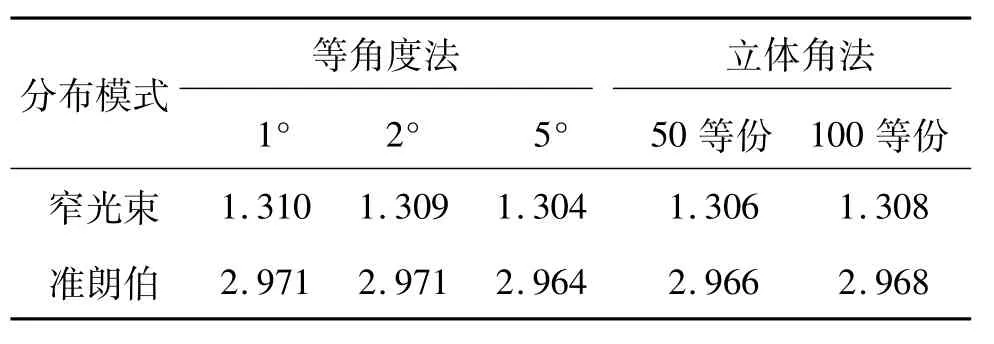
表3 采样间隔对光强分布类型LED的影响 lm
从表3数据可知,采用1°和2°等角度法和100等份立体角法所得的测量结果接近,相差不大于0.1%。5°等角度法和50等份立体角法与1°等角度法结果差异较明显,最大相差约0.46%,和理论计算结果相近。
对于不规则发光(峰值不在0°和90°)LED,则视为坐标轴旋转了一定的角度,其余计算过程不变,可获得类似的结果。
6 小 结
采用计算机模拟了分布光度计测量4种类型LED的总光通量量值过程。理论计算了采用不同的采样间隔对标定该4种类型的LED单管总光通量的系统误差。这4种类型LED的光强分布曲线分别是准朗伯分布、长茄形分布、双翼形分布、窄光束分布。计算结果显示,0.5°、1°等角度法测量总通量的系统偏差在0.05%左右。在测量精度要求高且不了解光源大概分布的情况下应采用这两种模式。若光源非窄光束分布,可适当减少采样间隔以提高采集速度,如,采用2°等角度法和50等份立体角法。对于常见的非轴对称情况的LED单管光源采用2°等角度法,在球带份数m值大于12的情况下,系统偏差可控制在0.3%以内。而对准确率要求比较高时,建议m值大于等于18。可以认为,LED光强分布虽多样化,但分布曲线大都是连续变化的,以上结论是可参考的。对于某些方向性极其强的LED,需针对实际情况,重新计算测量的系统误差。
[1]赵伟强,刘慧,等.基于6030电机控制卡的LED分布光度计小型化研究[J].计量技术,2011,(1):8-11.
[2]赵伟强,刘慧,等.高功率LED单管总光通量的测量技术[J].计量技术,2012,(9):25-27.
[3]赵伟强,刘慧,等.高功率与低功率LED管光色参数测量技术的异同[J].应用光学,2011,32(s1):61-64.
[4]刘建,刘慧,等.探测器响应度不均匀性对测量LED平均发光强度的影响[J].计量学报,2012,33(4):317-320.
[5]中国计量科学研究院自动分布光度计课题组.复合式大型自动分布光度计[J].计量学报,1983,4(4):250 -255.
[6]Commission Internationale de l'eclairage.CIE 127-2007:Measurement of LEDs[S].2007.
Effect of Sampling Interval on the Measurement of the Total Luminous Flux of LED
ZHAO Wei-qiang1,LIU Hui1,LIU Jian1,2,YANG Chen-zhu1
(1.National Institute of Metrology,Beijing 100029,China;2.Beijing Normal University,Beijing 100875,China)
With the computer to simulate LED spatial illuminance distribution and LEDs total luminous flux measurement process of a goniophotometer,showing the effect of different sampling interval on the measuring of four types of LEDs,whose intensity spatial distribution curves are of quasi-Lambert,tomato,double-wings,and narrow beam respectively.Axial or non-axial symmetric types are both considered.The calculation results show that,for common LED light source,a usage is recommended with a 2°interval and amount of sections greater than 12.The systematic error of sampling interval with a goniophotometer can be controlled within 0.3%.
Metrology;Luminous flux;Sampling interval;Computational simulation;LED;Goniophotometer
TB96
A
1000-1158(2015)01-0022-04
10.3969/j.issn.1000-1158.2015.01.06
2012-07-02;
2013-03-18
赵伟强(1981-),男,广东深圳人,中国计量科学研究院副研究员,博士,主要从事光度计量测试的研究。zhaowq@nim.ac.cn
