定积分中两个公式的推广与应用
2015-10-25郑玉军
郑玉军
(湖南科技学院 理学院,湖南 永州 425199)
定积分中两个公式的推广与应用
郑玉军
(湖南科技学院 理学院,湖南 永州 425199)
对两个定积分公式加以了推广与应用,在此基础上推导出了一些公式,运用这些公式可简化定积分的计算,提高计算定积分的效率。
定积分;公式;计算;推广
定积分是积分学中的一个重要问题,在理论研究和实际应用中,很多问题都归结为定积分的计算问题。而通常的方法是计算不定积分求原函数然后利用牛顿—莱布尼兹公式来计算,但有些被积函数本身形式复杂原函数并不容易求得,甚至有原函数无法用初等函数表示出来的。而对于一些特殊的定积分可采用一些特殊的方法和技巧来处理,如利用函数的奇偶性和被积区域的对称性、利用周期函数的性质等方法[1,2]来简化计算.本文对文献[3]中的两个定积分公式加以推广与应用,熟练掌握这些公式,可以大大提高计算定积分的效率,增强定积分计算的解题能力。
文献[3]中有如下两个公式:
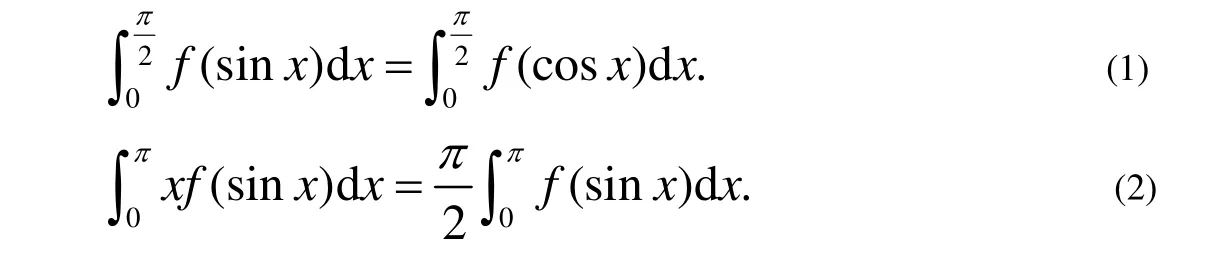
事实上我们还可以进一步推广,得到以下命题.
命题:若f( x)为连续函数,则



又当n为奇数时sinnx是奇函数,当n为偶数时sinnx是偶函数,故当n为奇数时时运用命题的
结论(1)和公式(4),有
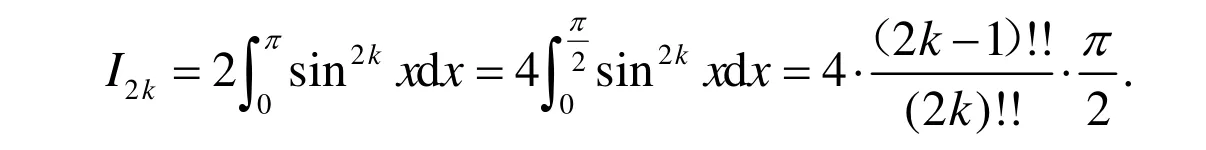
由于cosnx是偶函数,且是以2p为周期的函数,故
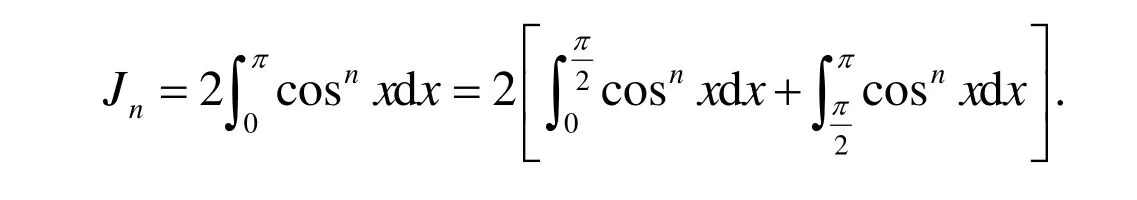
令x=p-u,则


[1]韦兰英.例谈定积分的计算方法和技巧[J]. 南宁师范高等专科学校学报,2008,25(4):112-114.
[2]罗威.定积分计算中的若干技巧[J]. 沈阳师范大学学报(自然科学版),2010,28(2):165-168.
[3]同济大学数学系.高等数学 (第六版) [M].北京:高等教育出版社,2007:248-253.
[4]复旦大学数学系.数学分析 (第二版) [M].北京:高等教育出版社,1983:292-301.
(责任编校:宫彦军)
O241.8
A
1673-2219(2015)05-0025-03
2015-03-29
湖南科技学院教学改革研究项目(湘科院教字2014[14]号)。
郑玉军(1982-),男,讲师,硕士,主要研究方向为计算数学。
