不定积分∫secnx d x的求解方法

邓宇龙张亚辉

（1.湖南科技学院 理学院， 湖南 永州 425199；2.衡阳县第五中学，湖南 衡阳 421236）

不定积分∫secnx d x的求解方法

邓宇龙1张亚辉2

（1.湖南科技学院 理学院， 湖南 永州 425199；2.衡阳县第五中学，湖南 衡阳 421236）

通过对不定积分的求解方法的探讨，以期帮助理解不定积分求解过程中的换元积分法和分部积分法。

不定积分；换元积分法；分部积分法；有理分式函数

求函数的不定积分是数学分析和高等数学的主要内容之一［1-3］。 最基本的求解函数不定积分的方法是换元积分法和分部积分法，很多函数的不定积分采用这两种方法可以得到圆满的解决。为了更好的理解换元积分法和分部积分法，本文将探讨不定积分的求解。

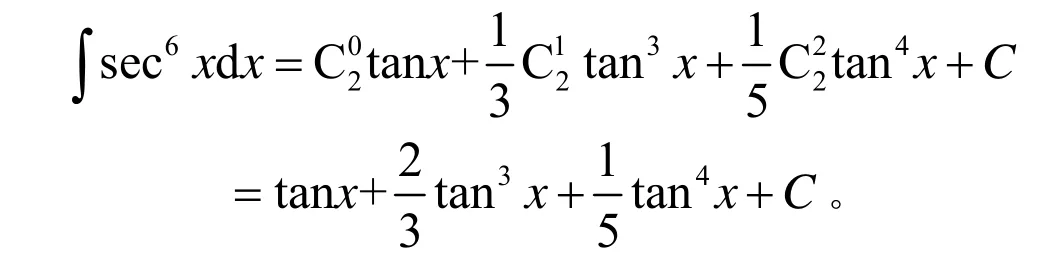
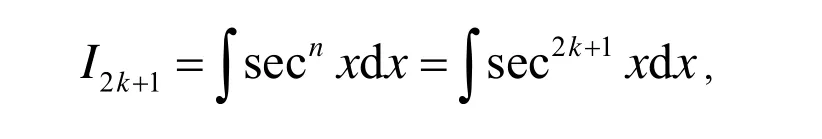
得到递推公式

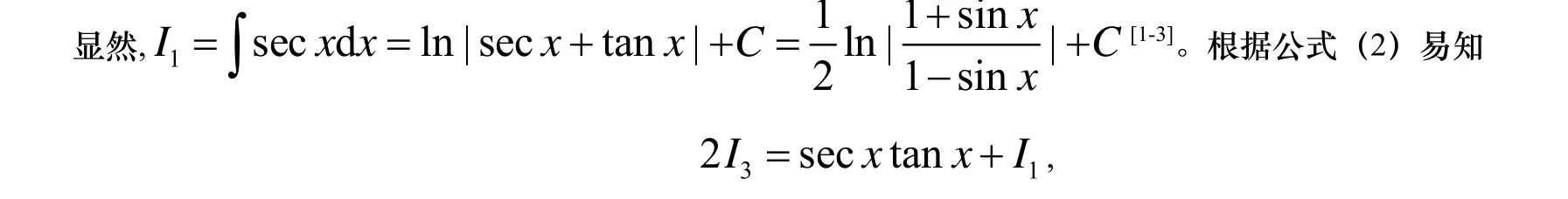
于是

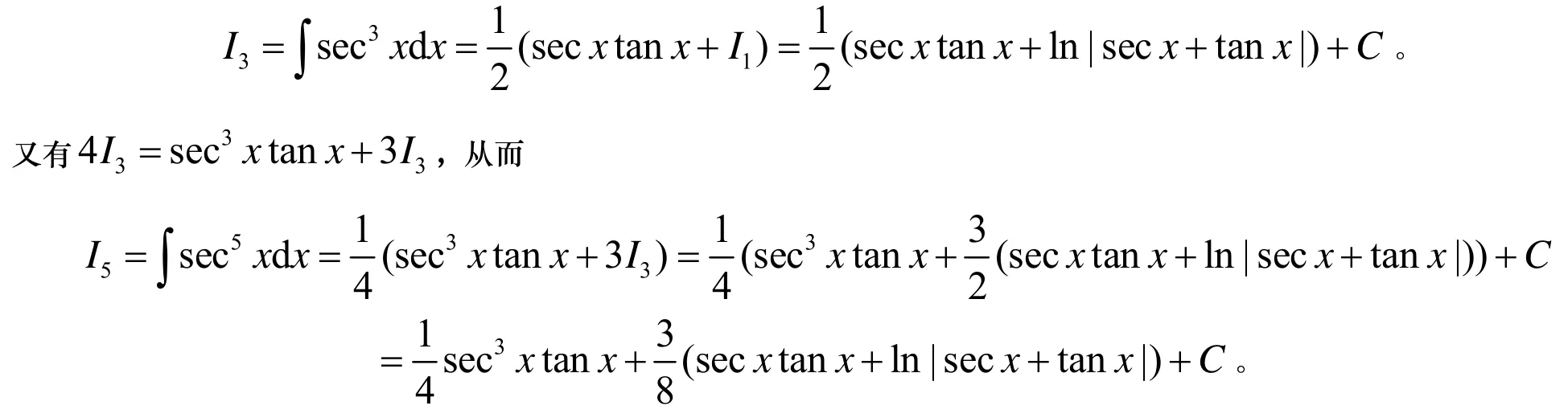
此外，I2k+1还可以转化为有理分式函数的积分进行求解。事实上，

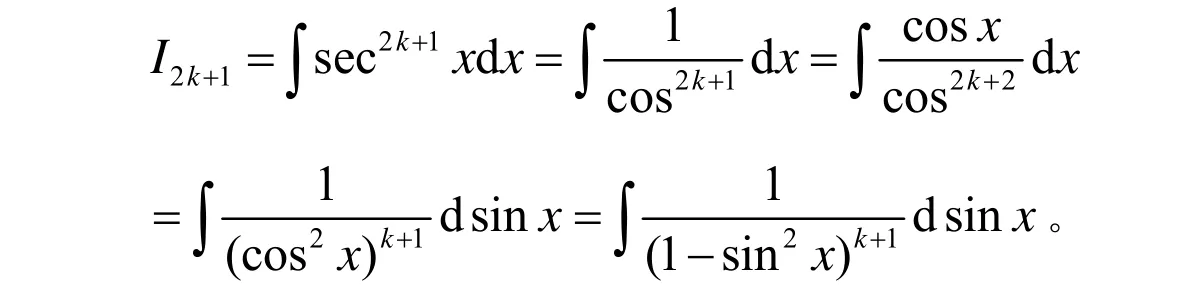
令u=sinx，则

［1］陈纪修，於崇华，金路.数学分析［M］.北京：高等教育出版社，2006.

［2］华东师范大学数学系.数学分析［M］.北京：高等教育出版社，2009.

［3］同济大学数学系.高等数学［M］.北京：高等教育出版社，2014.

［4］赵继红.关于不定积分∫secxdx的几种求解方法［J］.湖南文理学院学报（自然科学版），2012，24（1）：5-6.

（责任编校：宫彦军）

O171.1

A

1673-2219（2015）05-0021-04

2014－12－06

湖南科技学院教学改革研究项目（XKYJ2012028）资助。

邓宇龙（1980－），男，湖南蓝山人，硕士，讲师，主要研究方向为调和分析、密码学。