声自导鱼雷搜索波束优化分析
2015-10-25张静远
雷 鸣,张静远,饶 喆
(海军工程大学 兵器工程系,湖北 武汉,430033)
声自导鱼雷搜索波束优化分析
雷鸣,张静远,饶喆
(海军工程大学 兵器工程系,湖北 武汉,430033)
为了研究声自导鱼雷搜索波束对搜索效率的影响,以噪声掩蔽下主动声呐方程为基础,结合立体角计算公式,推导出声自导鱼雷搜索波束宽度和自导作用距离的关系式。根据蛇行搜索弹道特点建立蛇行弹道下的搜索面积模型,定量分析了不同因素对鱼雷搜索效率的影响,确定了最佳搜索波束宽度范围在15°~25°之间,所得结论可供声自导鱼雷基阵设计和作战使用参考。
声自导鱼雷; 蛇行弹道; 波束宽度; 搜索效率
0 引言
鱼雷是现代海战的重要武器,鱼雷搜索目标能力的强弱直接影响鱼雷的作战效能,而鱼雷搜索目标的能力由鱼雷自导作用距离、搜索扇面开角、发射信号波形、搜索策略和搜索弹道等多种因素共同决定[1-3]。一般情况下,自导作用距离远、搜索扇面角大,鱼雷的搜索能力就强。然而在鱼雷基阵发射功率一定的情况下,波束宽意味着指向性指数低,空间处理增益小,自导作用距离就近; 反之,要想获得较远的自导作用距离,发射波束的宽度就要窄。
由于鱼雷发射脉冲的时间间隔不小于自导作用距离所对应声传播时间的2倍,所以在同样时间内窄波束覆盖的搜索扇面角较小,而宽波束虽然能较快覆盖一定扇面的空间,但是对其对应的自导作用距离近,这就需要根据一定的原则对两者进行平衡,以获得最佳的搜索效果。
目前鱼雷声自导波束的设计是在基阵设计的基础上,采用幅度加权方式实现所需的波束宽度,再通过自导声功率、发射信号波形、信号处理方法以及与全雷自噪声的综合权衡,实现不小于一定值的自导作用距离,再根据弹道形式和搜索扇面的大致要求,确定波束扫描形式[4-5]。如此设计,可以解决工程应用问题,但是对搜索效率缺乏定量分析,实际作战条件下的搜索目标能力无法判定。对此,文章在限定基阵功率的情况下,定量分析波束宽度与自导作用距离关系,结合蛇行弹道特点建立搜索面积模型,以搜索效率为目标,确定了声自导鱼雷最佳波束宽度范围。
1 自导作用距离和波束宽度关系建模
主动声呐方程

式中: SL为发射声源级; NL为鱼雷自噪声级;TL为声波的单程传播损失; TS为目标强度;DT为检测阈。根据自导发射机电声转换方程[6]
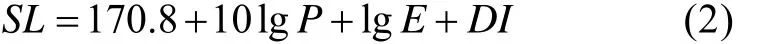
式中: P为自导发射机的电功率; E为发射效率;DI为发射换能器指向性指数,与波束宽度有关,带入式(1)得
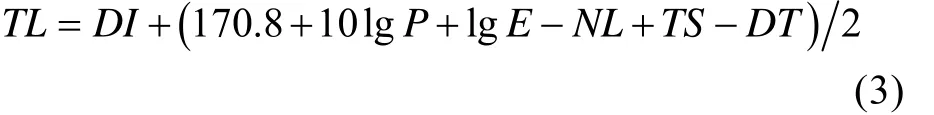
等式右侧的自导发射机的电功率P、换能器电声转换效率E、鱼雷自噪声级NL、目标强度TS、检测阈DT等均为固定值,用2C表示这几项之和。考虑球面扩展加吸收损失,有

将式(4)带入式(3)得
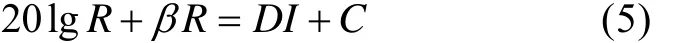
对于给定自导声基阵,有

式中: γ为聚集系数,与发射波束宽度有关;Imax为主极大方向上的声强; Iref为无方向性的发射声强,对于给定声自导系统来说为固定值。
将式(6)带入式(5),并交换方程有
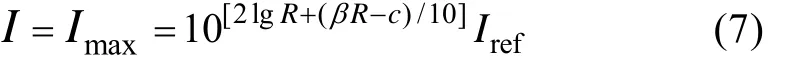
假设有2种波束,0Ω和1Ω分别为2种波束对应的空间立体角,R0和R1分别为自导作用距离,I0和I1分别为在自导作用距离处的声强,S0和S1分别为波束在自导作用距离处传播曲面的面积,20α和21α为波束水平角。根据式(7)可以求得

当水平与垂直面波束开宽度相等时,空间立体角为[7]

式中: S为声传播曲面面积; R为自导作用距离;α为波束宽度的一半。假设声波按照球面扩展传播,根据声功率相等可以得到

将式(9)代入式(10)得

将式(8)带入式(11)有
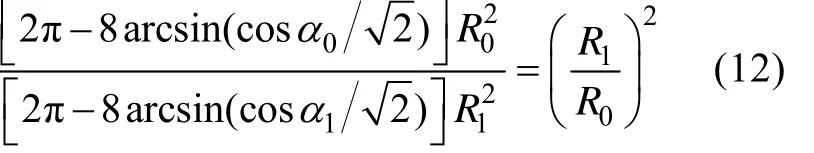
以美国MK46鱼雷为例,其基阵自然半波束宽度α=14°,波束形成后的半波束宽度α=8°,自导作用距离为1 350 m,可以推得其自然波束下的作用距离为1 100 m。并由此可得自导作用距离和波束宽度的关系
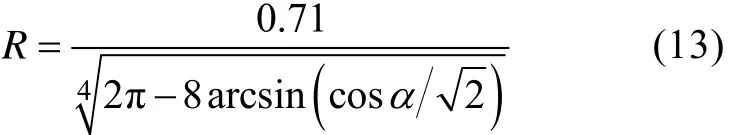
为确保下一个脉冲发射之前换能器能够接收到上一个脉冲的回波,最大作用距离Rmax与脉冲发射周期Tbeam必须满足

其中: C0为声波在海水中的传播速度。
2 蛇行搜索弹道下搜索面积建模
2.1蛇行搜索最佳角速度的确定
当鱼雷到达主航向后以角速度φ向左或向右旋回直至某一角度λ(此角度称为蛇行视角的一半),再以同样的角速度反向旋回至角度λ,此后鱼雷就在主航向左右λ处交替进行蛇行搜索。角速度太快、波束太窄会使得相邻波束之间存在空隙而有可能造成目标的遗漏; 角速度太慢、波束太宽又会使得相邻波束之间存在重叠导致搜索效率的下降,而波束宽度与自导作用距离、脉冲发射周期存在关系,只有对角速度、波束宽度、脉冲发射周期等因素进行匹配后才能获得最佳的搜索效果。要想使得相邻波束之间无空隙且不重叠,必须满足

2.2蛇行搜索扇面的等效方法
鱼雷以蛇行方式对目标进行搜索时(见图1),假设其速度为v,角速度为φ,蛇行视角为2λ,自导作用距离为R,发射波束宽度为2α,则等效航速[8]

等效扇面参数为
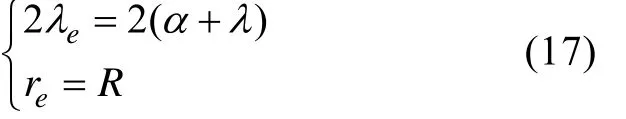
即鱼雷在1个搜索周期内自导扇面的扫描区可等效为自导作用距离为R,扇面开角为2(α+)λ的扇面。

图1 蛇行弹道下鱼雷搜索面积模型Fig. 1 Model of torpedo searching area for snake-searched trajectory
2.3蛇行弹道下搜索面积建模
鱼雷在由一个搜索周期Ts内的搜索面积
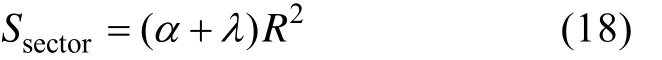
搜索周期

为简便起见,可认为在一个搜索周期内鱼雷是“静止”的,在下一个搜索周期开始时,鱼雷会发生向前的“跃变”,而“跃变”的距离

每个搜索周期内的新增搜索面积

由于鱼雷的“跃变”导致在每个搜索周期内存在部分区域无法被扫描到以致存在搜索遗漏,此遗漏部分的面积可表示为
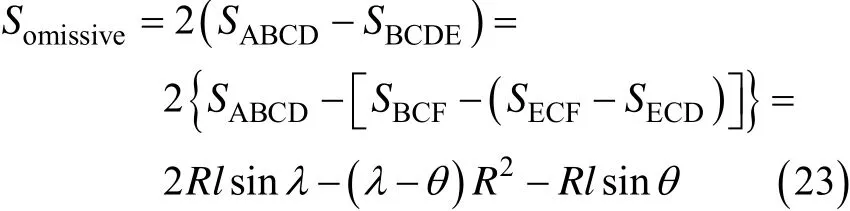
定义1: 每个搜索周期内遗漏面积与新增面积和遗漏面积之和的比值为遗漏面积率
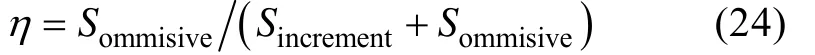
定义2: 每个搜索周期内新增面积与搜索周期的比值为单位时间新增搜索面积

3 计算结果与分析
3.1单位时间新增搜索面积与波束宽度关系计算
当鱼雷速度为45 kn,蛇行视角分别为60°,90°,120°时,单位时间内新增搜索面积与波束宽度关系如图2所示。
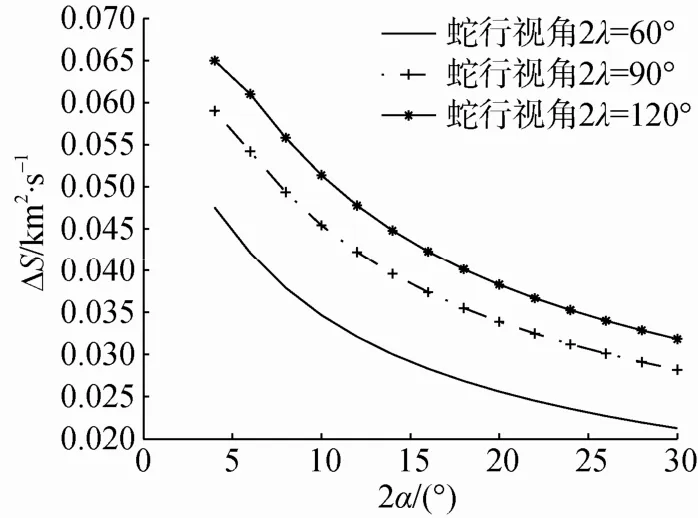
图2 单位时间新增搜索面积与波束宽度关系图Fig. 2 Relationship between incremental searching area in unit time and beamwidth
由图2可知,蛇行视角固定不变时,由于每个搜索周期内宽波束对应的新增搜索面积少于窄波束对应的新增搜索面积,故单位时间新增搜索面积随着波束宽度的增加而减少; 对于宽度固定的波束来说,由于在每个搜索周期内大蛇行视角对应的新增搜索面积大于小蛇行视角对应的新增搜索面积,故蛇行视角越大对应的单位时间新增搜索面积越多。
3.2搜索面积遗漏率与波束宽度关系的计算分析
当鱼雷速度为45 kn,蛇行视角分别为60°,90°,120°时,搜索面积遗漏率与波束宽度的关系如图3所示。
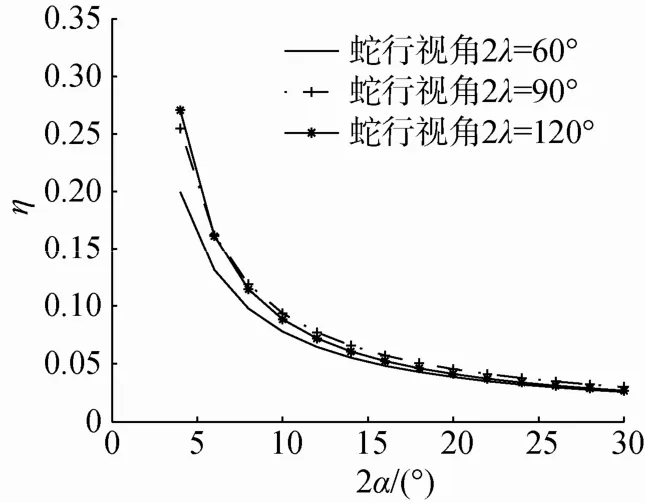
图3 搜索面积遗漏率与波束宽度关系图Fig. 3 Realationship between omitting-rate of searching area and beamwidth
由图3可知,搜索面积遗漏率随着波束宽度的增加而减少,原因是窄波束对应的蛇行周期较长导致遗漏面积较大,随着波束宽度的增加,遗漏面积逐渐减少,最后遗漏面积与新增面积的比值趋于稳定。
3.3搜索面积遗漏率与蛇行视角关系的计算
鱼雷速度为45 kn,波束宽度分别为10°,20°,30°时,搜索面积遗漏率与蛇行视角的关系如图4所示。
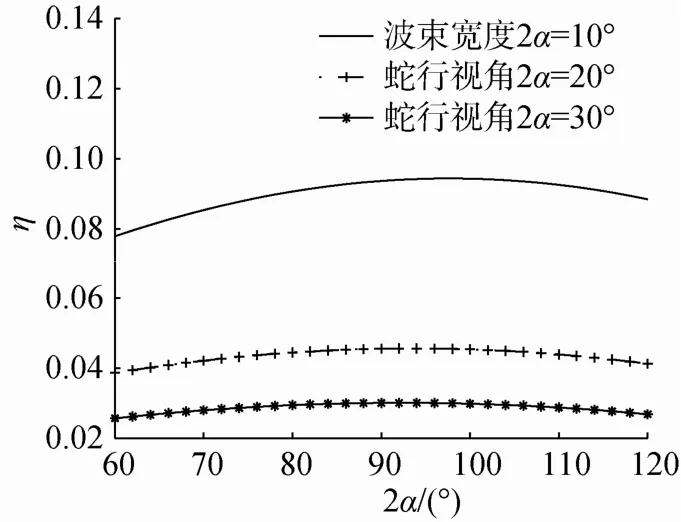
图4 搜索面积遗漏率与蛇行视角的关系Fig. 4 Relationship between omitting rate of searching area and snaking angle
由图4可知,不同蛇行视角下搜索面积遗漏率相差不大,故蛇行视角的大小对搜索面积遗漏率的影响可忽略不计。
3.4鱼雷速度对单位时间新增搜索面积的影响
蛇行视角为90°,鱼雷速度分别40 kn,45 kn,50 kn时,单位时间新增搜索面积与波束宽度的关系如图5所示。
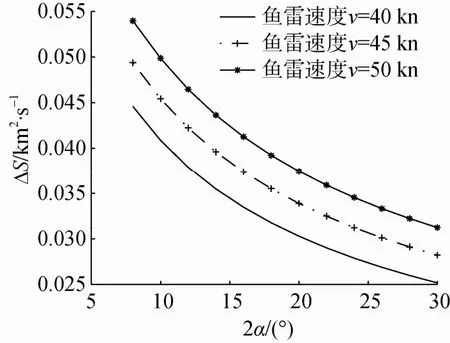
图5 鱼雷速度不同时单位时间新增搜索面积与波束宽度的关系Fig. 5 Relationship between incremental searching area in unit time and beamwidth at different torpedo speed
由图5可知,速度较快的鱼雷对应的单位时间新增搜索面积较大,原因是当蛇行视角和波束宽度固定时,鱼雷的搜索周期固定不变,鱼雷速度越快对应的单位时间新增搜索面积越大。
3.5射程对单位时间搜索面积的影响
当蛇行视角为90°,鱼雷速度为45 kn,射程分别为3 km,5 km,7 km时,单位时间搜索面积与波束宽度的关系如图6所示。
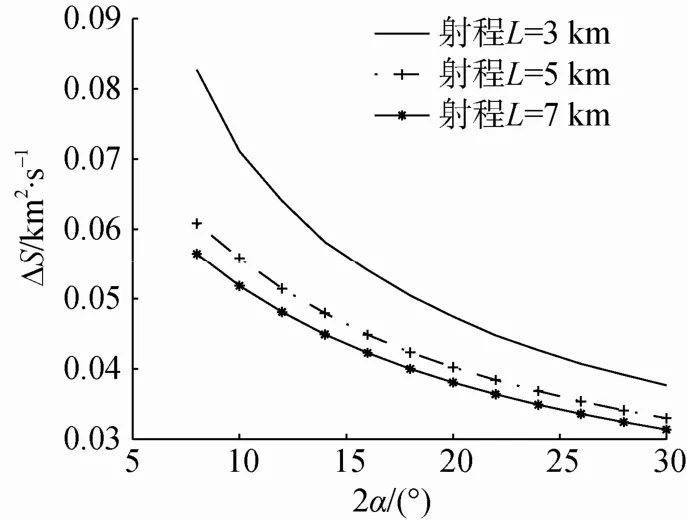
图6 射程不同时单位时间搜索面积与波束宽度的关系Fig. 6 Relationship between searching area in unit time and beamwidth in different torpedo range
由图6可知,射程较近时对应的单位时间搜索面积较大,因为鱼雷在第1个搜索周期内的搜索面积最大,在接下来的每一个搜索周期内新增搜索面积小于首个搜索周期的搜索面积,搜索面积与搜索时间的比值随着射距的增加而减少。
3.6结果分析
综合以上分析可知,窄波束对应的搜索面积遗漏率较大,普遍大于5%,有的甚至超过20%; 宽波束对应的单位时间新增搜索面积较小导致搜索效率较低; 而宽度在15°~25°的波束可以兼顾搜索效率和搜索面积遗漏率,所以选择宽度在15°~25°的波束较为合适。
虽然大蛇行视角对应的单位时间新增搜索面积较大,但是大蛇行视角平行于主航向的速度较小,不利于快速接近目标且会消耗更多的航程,导致鱼雷用于攻击的航程减少,进而影响鱼雷的命中概率。因此蛇行视角的选取要综合考虑众多因素后确定。
4 结束语
由于目前声自导鱼雷搜索波束的设计大多是基于经验,在鱼雷搜索效率方面缺乏定量分析。文中通过噪声掩蔽下的主动声呐方程和空间立体角计算公式,推导出波束宽度与自导作用距离的关系式,结合蛇行搜索弹道特点建立蛇行弹道搜索面积模型,通过分析影响鱼雷搜索效率的因素,得到声自导鱼雷最佳波束宽度为15°~25°,所得结论可供声自导鱼雷基阵设计和作战使用参考。
[1] 荆雪艳. 鱼雷自导作用距离评估[J]. 鱼雷技术,2000,8(1): 26-29.
[2] 张学锋,潘光,王鹏. 火箭助飞鱼雷水下水平发射弹道设计[J]. 鱼雷技术,2007,15(4): 11-13.
Zhang Xue-feng,Pan Guang,Wang Peng. Underwate Trajectory Design of Rocket-assisted Torpedo[J]. Torpedo Technology,2007,15(4): 11-13.
[3] 李斌,范若楠,倪文玺. 基于弹道仿真的鱼雷性能优化方法[J]. 鱼雷技术,2015,23(3): 172-176.
Li Bin,Fan Ruo-nan,Ni Wen-xi. An Optimization Method of Torpedo Performance Based on Trajectory Simulation[J]. Torpedo Technology,2015,23(3): 172-176.
[4] 李贵斌. 声呐基阵设计原理[M]. 北京: 海洋出版社,1993.
[5] 周德善. 鱼雷自导技术[M]. 北京: 国防工业出版社,2009.
[6] Urick R J. Principles of Underwater Sound for Engineers[M]. New York: McGraw-Hill Book Company,1975.
[7] 初醒悟. 立体角计算公式[A]. 走进CIE 26th[C]//上海:中国照明学会(2005)学术年会,2005,9.
[8] 张静远. 鱼雷作战使用与作战能力分析[M]. 北京: 国防工业出版社,2005.
(责任编辑: 杨力军)
Optimization of Searching Beam for Acoustic Homing Torpedo
LEI Ming,ZHANG Jing-yuan,RAO Zhe
(Department of Weaponry Engineering,Naval University of Engineering,Wuhan 430033,China)
To understand the influence of acoustic homing torpedo searching beam on searching efficiency,the relation between torpedo searching beam width and homing range is derived based on the active sonar equation and the solid angle formula. According to the characteristics of snake trajectory,a model of torpedo searching area is built. The influences of various factors on torpedo searching efficiency are quantitatively analyzed,and the optimized beam width range from 15°to 25°is determined. This study may provide a reference for design of sonar array and operational application of an acoustic homing torpedo.
acoustic homing torpedo; snake trajectory; beam width; searching efficiency
TJ630.34
A
1673-1948(2015)05-0338-05
10.11993/j.issn.1673-1948.2015.05.004
2015-07-17;
2015-08-10.
雷鸣(1990-),男,在读硕士,研究方向为武器制导与控制.
