基于田口方法的铝合金轮毂造型最佳化设计研究

吴俭涛，陈永亮

（燕山大学艺术与设计学院，河北秦皇岛066004）

基于田口方法的铝合金轮毂造型最佳化设计研究

吴俭涛*，陈永亮

（燕山大学艺术与设计学院，河北秦皇岛066004）

应用4因子3水平正交实验建构9组轮毂样本，利用田口方法的望小品质特性结合有限元软件对轮毂剖面、轮辐数量、螺栓孔数及窗口大小4项轮毂造型因子进行信噪比分析，以期获得铝合金轮毂的最佳化设计因子组合。结果表明：轮毂最佳化设计因子组合为轮毂剖面a样式、轮辐数为8辐、螺栓孔数为6孔、窗口大小为y造型。轮毂实体样本测试结果与I-DEAS模拟分析数据相符合，证明田口方法结合有限元软件进行轮毂最佳化设计具有可行性。

铝合金轮毂；田口方法；有限元分析；最佳化设计

0　引言

铝合金轮毂最佳化设计是融入结构分析、美学特性等因素的综合性优化解决方案，借以开发出质优、量轻、美观的轮毂产品。近年来，各大轮毂厂商纷纷引入计算机模拟分析软件对轮毂结构等方面进行模拟预判等相关研究。郭威成［1］运用有限元分析方法及台架试验对轮毂失效情况进行模拟分析，并进行了实际验证。孙利［2］提出铝合金轮毂造型设计中应引入技术美学的设计理念，并利用ABAQUS软件进行了虚拟台架试验有限元分析，得到了轮毂正面和背面容易失效或破坏的部位及其变化规律。李宏禹［3］提出造型与结构设计一体化的轮毂开发方法。赵亮［4］利用ANSYS软件对镁合金轮毂进行了结构优化设计。Hsu Yeh-Liang［5］探讨了铝合金轮毂在疲劳限制条件下的减重设计，通过优化逃料孔特征参数，求解出最优的逃料造型以达到减重目的。

现有研究多以有限元软件模拟分析轮毂结构以达到优化设计的目的，或是探讨轮毂造型与结构一体化的轮毂开发方法，但在轮毂造型的强度优化问题方面的研究较少。本文将轮毂造型分解为轮毂剖面、轮辐数量、螺栓孔数及窗口大小4个造型因子，结合田口方法的望小特性并通过信噪比分析正交试验结果，得出不同轮毂造型因子对轮毂结构强度的影响及规律特征。结合试验进一步验证轮毂造型多因子优化，即轮毂造型最佳化设计的可行性。

1　田口方法在铝合金轮毂设计中的应用

田口方法由田口玄一博士结合变异数分析法和直交表发展而成，它是一种改善产品质量问题的优化方法［6-7］，其中田口直交表的目的是以最少的时间与成本决定出最佳的设计参数［8］，直交表的选取取决于目标函数的总自由度，总自由度即是分析目标函数所需的最少实验次数［9］。田口方法将信噪比作为衡量产品质量的标准，其主要目的是用来衡量产品质量的稳定性，S/N比越高表示损失越少，质量越稳定［10-11］。静态质量特性有3种S/N比，分别是望小特性、望大特性以及望目特性，其中望小特性是指质量特性越小越好，其为连续且非负值，理想的质量特性目标值为零，并且无可调因子存在［12］；望大特性是指品质特性为越大越好，其为连续且非负值，理想的品质特性目标值为无限大，并且无可调因子存在［13］；望目特性是指品质特性目标值为M，其最佳值与目标值一致，当品质特性越接近目标值品质越佳，一般具有可调因子［14］。铝合金轮毂最佳化设计以轻量化和受应力最小为目标，所以使用望小特性作为品质特性进行实验为最佳。本文将铝合金轮毂造型要素进行分解，并应用田口方法绘制轮毂样本直交表，结合I-DEAS有限元软件进行力学分析，以期用最少的实验次数衡量轮毂质量的稳定性。通过对轮毂四大因子信噪比的分析，找出贡献度较大的影响因子，从而得到轮毂最佳化设计参数组合。

2　基于田口方法的铝合金轮毂造型最佳化设计实验

基于田口方法的轮毂造型最佳化实验步骤如图1所示。

图1　田口方法实验步骤Fig.1 Experimental procedure of Taguchi method

实验主要包括7个步骤：轮毂品质特性选取、信噪比判定、轮毂造型因子确定、直交表选择、正交试验、试验分析及实体轮毂样本测试。与轮毂造型密切相关的品质特性主要是重量及强度，本研究将两项品质特性具体化为质量最轻与受应力最小两项评价指标。评价指标的信噪比可分为望大特性、望小特性及望目特性，质量最轻与受应力最小两项指标皆符合望小特性。将所有影响品质的轮毂样式及形式特征进行罗列，通过分类整理归并确定为四类造型因子：轮毂剖面、轮辐数量、螺栓孔数及窗口大小。按照造型因子的数目及样式的数目选用适当的直交表，这里选定直交表L9（34）。按照直交表的配置，对每一组参数进行试验，并且记录数据。将每一组测量数据分别计算其信噪比S/N，并且制作响应表探讨各因子对于品质特性的效应，找出造型因子最佳组合。通过试验分析得出最佳因子组合方案，利用成型设备获得其实体轮毂样本。对实体样本进行冲击、弯曲及径向测试，由测试结果验证最佳因子组合方案的强度合理性。

3　铝合金轮毂最佳化设计模拟实验

3.1有限元模拟分析与田口实验

结合I-DEAS有限元分析软件配合田口实验法，对轮毂受到冲击时的变化进行模拟实验，由于结构强度和负载与应力分布有关系，所以将由IDEAS分析出来的应力与重量数据代入田口实验得到最佳化设计目标。依据专家组经验及集体讨论，将影响轮毂重量和强度特性的主要造型因子划分为4类：轮毂剖面、辐条数、螺栓孔数、窗口大小。本研究选择3款不同轮毂样式进行田口实验设计，以其获得最佳造型因子组合方案。3款不同样式轮毂的造型因子对应关系如表1所示。

表1　轮毂造型因子对应表Tab.1 Map table of factors in wheel hubs design

轮毂剖面样式如图2所示，分别为a样式、b样式、c样式。轮毂辐条数量如图3所示，分别为5辐、6辐、8辐。螺栓孔数如图4所示，选用常用的3种不同孔数4孔、5孔、6孔。窗口大小如图5所示，分别为x样式、y样式、z样式。

依据田口方法，每个控制因子有3个样式，自由度为2，共有4个控制因子，所以总自由度为8，最终选取自由度为8的L9（34）直交表，按照此直交表排列因子与样式组合，得到9组实验配置表，如表2所示。

图2　轮毂剖面样式Fig.2 Profile of wheel hub

图3　轮毂辐条数量Fig.3 Quantity of spoke

图4　轮毂螺栓孔数Fig.4 Quantity of bolt hole

图5　轮毂窗口大小Fig.5 Size of the window

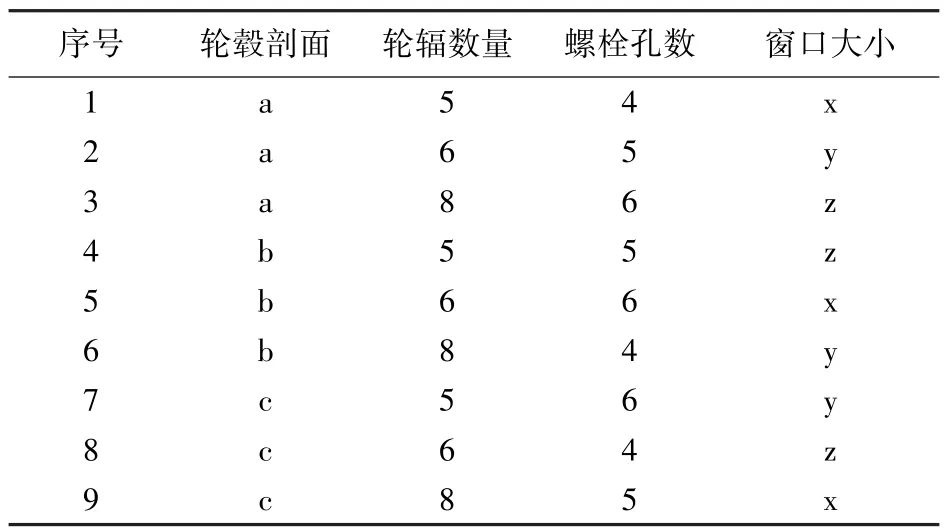
表2　L9（34）正交试验方案Tab.2 Four factors three levels orthogonal experiment

将9组实验组合进行有限元模拟分析得到应力值，将得到的应力值和载荷值导入田口实验，利用望小特性公式计算出9组数据的S/N比，结果如表3所示。实验数据所得应力值越小，则S/N比的数值越小，表明其品质特性越好。

表3　正交试验结果Tab.3 Results of orthogonal experiment

根据表3可知，第3组组合的应力值与S/N值最小，该造型因子组合的结构强度较好，轮毂因子最佳组合应该出现在第3组试验对应的因子组合附近。第8组应力值与S/N值最大，表示该造型因子组合的结构强度较弱。

3.2应力值响应表分析结果

响应表可以判断各因子对于实验的重要程度，并且能够准确得出各因子的最佳样式组合。由表4应力值响应表中各因子S/N比和极差值，可以得出：轮毂造型四因子最佳组合为a样式剖面、8轮辐、6孔和y窗口大小（分别取各项信噪比最小值）。计算该最佳组合应力值为38.22 MPa，接近正交试验中第3组试验数据。利用成型设备获得该最佳化组合的轮毂实体样本，并进行强度测试。

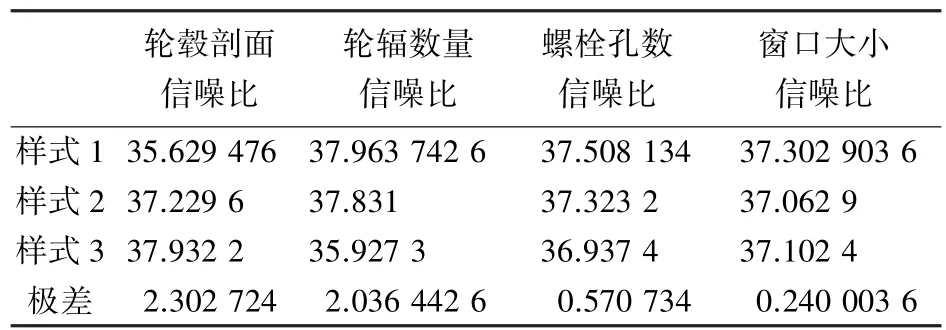
表4　各样式的应力值信噪比Tab.4 Stress value signal-to-noise ratio of different model

4　轮毂实体样本测试

利用成型设备，获得2号组、8号组、以及最佳组合组共3组的轮毂实体样本。利用测试机分别对3组不同造型因子组合的轮毂样本进行强度测试，获得不同样本的内部应力值，见表5。

表5　3组轮毂样本内部应力表Tab.5 Inner stress of 3 groups of wheel hubs samplesN

由表5可知，最佳组合组的内部应力最小，其结构强度最高。8号组内部应力最大，结构强度最小，与表3正交试验结论相一致。

5　结束语

本文以结构强度与轻量化为目标，利用田口方法的望小特性与有限元分析软件I-DEAS进行轮毂优化设计，经过交试验与分析计算得到轮毂的最优化设计组合为a样式剖面、8轮辐、6孔、y窗口大小的组合。经轮毂实体样本强度测试，结果与正交试验结论相符。田口方法结合有限元分析可大量减少样本测试规模和次数，提高最佳化设计方案的获取效率，为轮毂造型创意方案快速优化提供了一个可行的方法和途径。

［1］郭威成.铝合金轮毂的有限元分析［D］.秦皇岛：燕山大学，2013.

［2］孙利.铝合金轮毂设计的技术美学基础及应用研究［D］.秦皇岛：燕山大学，2014.

［3］李宏禹.汽车轮毂造型与结构设计一体化方法研究［D］.秦皇岛：燕山大学，2010.

［4］赵亮.基于ANSYS镁合金轮毂的结构优化设计［D］.秦皇岛：燕山大学，2013.

［5］Hsu Y L，Hsu M S.Weight reduction of aluminum disc wheels under fatigue constraints using a sequential neural network approximation method［J］.Computers in Industry，2001，46（2）：167-179.

［6］茆诗松，王金玉.田口思想及方法的研究［J］.自然杂志，1991，14（3）：163-169.

［7］金旭星.基于田口法的端铣刀研磨参数优化设计［J］.机械设计与制造，2013（5）：235-237.

［8］汪先送，程佩，张卫文，等.基于田口法的AI-Cu合金挤压铸造工艺参数化优化［J］.特种铸造及有色合金，2012，32（5）：447-450.

［9］杨菊英，郑金.试验设计法优化汽车内饰板成型工艺参数［J］.模具工业，2013，39（8）：21-24.

［10］CHEN Bin-qiang，ZHANG Zhou-suo，ZI Yan-yang，et al.A pseudo wavelet system-based vibration signature extracting method for rotatingmachineryfaultdetection［J］.ScienceChina（Technological Sciences），2013，56（5）：1294-1306.

［11］谢志平，苏明，郑继明，等.基于信噪比和灰关联度的电火花加工Ti-6Al-4V工艺参数优化［J］.煤矿机械，2012，33（11）：134-136.

［12］刘春涛，林志航.望大望小特性的模糊健壮设计研究［J］.西安交通大学学报，2005，39（9）：941-945.

［13］赵延明，郭迎福，文泽军，等.基于服役寿命分布的产品望大特性质量损失建模［J］.机械设计与研究，2013，29（4）：11-15.

［14］张志红，何桢.郭伟.望目特性稳健参数设计优化标准的构建［J］.机械工程学报，2008，44（4）：133-137.

Research on optimization design of aluminum alloy wheel hubs based on Taguchi method

WU Jian-tao，CHEN Yong-liang
（School of Art and Design，Yanshan University，Qinhuangdao，Hebei 066004，China）

With L9（34）orthogonal table for Aluminum alloy wheel design factors，the Taguchi＂small-the-better＂and the finite element analysis can provide the best optimized factors combination among wheel profile，quantity of spokes，bolt hole number and the size of the window.The signal to noise ratio shows that the best optimization is the combination：a style，8 spokes，6 bolt hole and y window.Consistent with the results of simulation test，the wheel hub entity sample test further validates the feasibility of the best optimal design.

aluminum alloy wheel hubs；Taguchi method；finite element analysis；optimal design

TB472

A DOI：10.3969/j.issn.1007-791X.2015.06.010

1007-791X（2015）06-0531-04

2015-09-18 基金项目：燕山大学青年教师自主研究计划课题社科A类（13SKA009）

*吴俭涛（1976-），女，吉林省吉林市人，博士研究生，副教授，主要研究方向为工业设计、轮毂设计，Email：wjt1949@ysu. edu.cn。