基于网格数值耗散修正的圆湍射流模型

刘正先，张晓星，张丽杰，罗纪生

（天津大学机械工程学院，天津　300072）

基于网格数值耗散修正的圆湍射流模型

刘正先，张晓星，张丽杰，罗纪生

（天津大学机械工程学院，天津300072）

基于民用机舱内个性通风口，以圆湍射流作为研究对象，以标准κ-ε湍流模型较精细数值模拟与实验对比结果为出发点，通过对粗网格下数值结果的分析，针对网格尺度增大导致计算中数值耗散相应增大、射流速度沿轴向和径向衰减过快问题，从湍流耗散率方程出发，对影响湍流耗散的生成项和耗散项进行修正，平衡因网格尺度产生流动衰减过快的因素，进而提出了耗散率修正的κ-ε湍流模型.采用该修正模型验证了不同雷诺数和非等温条件下射流的适用性.应用修正的湍流模型可以避免机舱内大尺度空间流动对网格的苛刻要求，明显减少网格总数，同时达到对舱内复杂结构和边界条件下流场特征的正确模拟.

个性化送风口；数值模拟；湍流模型；湍流耗散率

民用客机正日益成为越来越重要的交通工具，飞机座舱内的空气流通和品质成为考核座舱舒适度的重要指标［1］.舱内送风口使空气射流与舱内空气混合，达到通风换热目的，对舱内气流组织起着至关重要作用.采用计算流体力学（computational fluid dynamics，CFD）方法对舱内空气流动进行数值分析时，一方面为了得到送风参数的微观信息，要求计算网格达到毫米量级；另一方面为了能反映整舱内湍流涡旋特征对空气流动的影响，计算域则需达到几十米量级.这对送风口数值网格的生成、舱内网格的匹配以及计算机的容量均提出了巨大挑战.为此，国内外学者们提出了各种不同的风口描述方法和风口模型［2-5］.针对个性化送风口的模型目前主要有两类描述方法：间接描述的盒子类风口模型和直接描述类风口模型.间接描述模型有盒子方法［6-7］、指定速度法［8］和主流区法［9］，这些方法把送风口入流边界条件的描述转化到包围送风口的一个盒子边界上，借助实验值或者射流公式描述边界条件，避免了对送风口复杂流动情况的直接描述，但需要出风速度等物理参数的详细数据.直接描述类风口模型包括基本模型［10］和动量模型［11］等.基本模型采用具有相同有效面积的一个或多个矩形开口替代复杂形状的通风口.动量模型则采用具有相同总面积、质量流量和动量流量的开口来代替真实出风口，因为在边界条件处分别定义连续性方程和动量方程，在实际CFD模拟中存在一定问题［12］.

值得注意的是Nielsen［13］于1992年提出直接利用计算机模拟得到风口入口条件，但由于室内通风口的形状均较复杂，导致数值网格的划分困难，不能保证计算结果的正确性.同时需要耗费大量计算资源，这给其在实际工程中的应用带来了困难.该方法目前并未被人们采用，但是对本文中基于MD-82飞机的个性通风口来说，单独的风口计算模拟是可行的.

本文在借鉴Nielsen［13］直接模拟的基础上结合盒子类风口模型，先对基于MD-82的简化个性化送风口进行较精细数值模拟.然后针对粗网格对数值耗散沿径向和轴向射流衰减的影响，修正湍流模型中的耗散方程，使数值耗散达到与小尺度网格一致，将修正耗散率后的湍流模型，在以个性化通风口为背景的湍流射流流动中进行验证.

1　个性化送风口数值模拟与分析

1.1个性化送风口

研究对象为MD-82机型中某型号个性化通风口，图1为送风口外观，送风口类似为环状结构. Ferdman等［14］的研究指出圆湍射流在远场处的发展与射流初始速度剖面形状相独立，这意味着在远场处环形湍射流与圆形湍射流具有相同的特性.故此，本文用圆湍射流替代实际个性化送风口射流.

图1　个性化送风口外观Fig.1 Schematic of p ersonalized air supply opening

圆自由射流的整体结构较复杂，为便于分析常根据不同的流动特征将射流划分为3个区域：起始段、过渡段和主体段.由喷口出口边界起向内外扩展的剪切流动区称为紊动混合区，此区域射流中心部分未受紊动混掺影响，保持喷管出口速度的区域称为射流的起始段.在起始段下游区域绝大部分为充分发展的紊动混掺区，称为射流的主体段.流体经过充分混合以后即进入主体段，这时，沿中心轴线各横截面上的无量纲时均速度剖面具有相似性.在起始段与主体段之间有过渡段.图2为圆射流的分区示意.过渡段较短，在分析中为简化起见常被归入到起始段.不同求解方法得到的圆射流的起始段长度均为喷口直径的6倍左右［15］，这是一段比较短的距离，尚未达到机舱内人体个性化微环境关心的区域，因此在通风过程中更关注主体段.

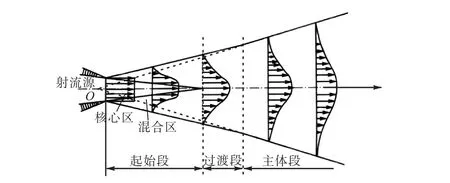
图2　圆射流的分区示意Fig.2 Partition schematic of round jet

1.2计算域与网格划分

数值计算域、边界条件及坐标系设置如图3所示.由于在真实的座舱环境下个性化送风口的流量控制在20～40，L/min左右，即相应雷诺数为1，000～2，000，因此射流Re（Re=v0D/υ）取1，000，其中v0为射流出口速度，D为圆射流出口直径，υ为流体的运动黏度系数.坐标系如图3所示，z为射流流向位置，坐标原点位于送风口中心处.

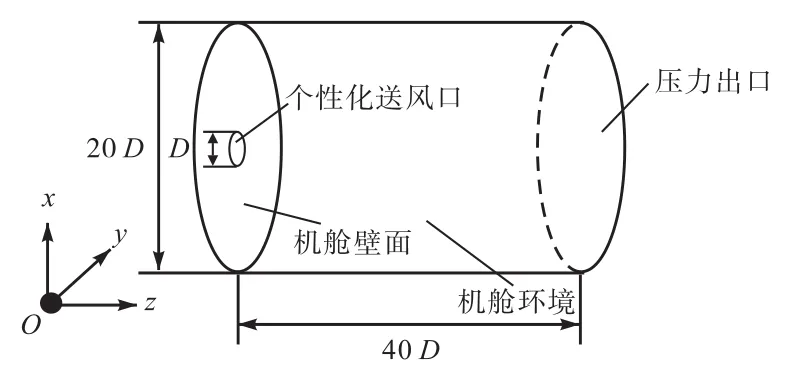
图3　计算域、边界及坐标设置示意Fig.3Computational domain，boundary and the coordinate system

计算采用结构网格，如图4所示，在射流入口以及过渡段流动变化较剧烈的区域局部加密，最小网格尺度为0.000，7，m，网格总数约为56×104.对于入口边界采用速度入口，出口以及计算域侧面采用压力出口边界，计算域上边界为无滑移壁面（见图4）.计算流体介质为不可压缩空气.采用二阶迎风格式的有限体积法对控制方程进行数值模拟，控制方程包括连续性方程、动量方程、湍动能方程、耗散率方程等.收敛指标为1× 10-5.

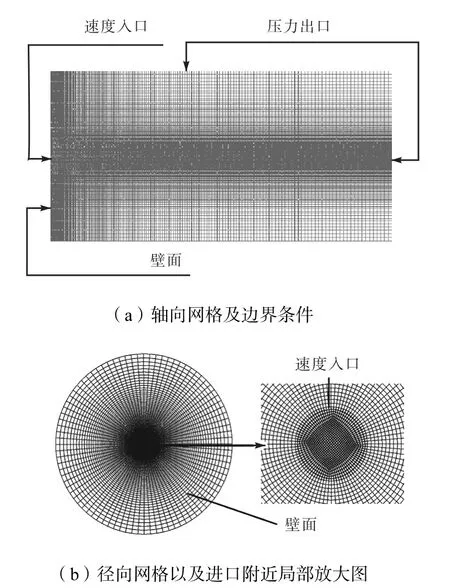
图4　轴向和径向网格分布Fig.4 Mesh in axial and radial direction

1.3湍流模型

经对比试算，最终确定首先采用标准κ-ε湍流模型对圆湍射流进行较小尺度网格下的数值模拟.该湍流模型将湍动能κ以及湍动耗散率ε方程引入封闭雷诺平均方程（RANS）［16］.当流动为不可压且不考虑自定义源项时，湍动能方程为

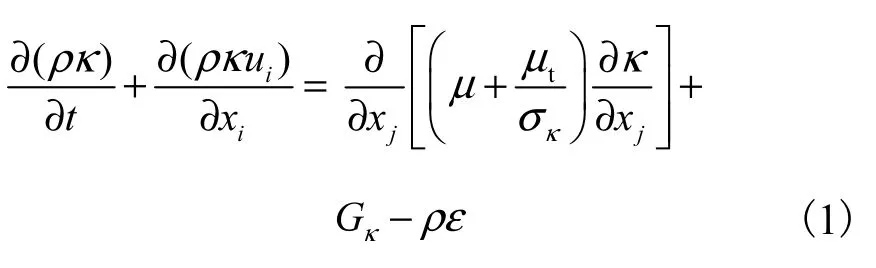
耗散方程为

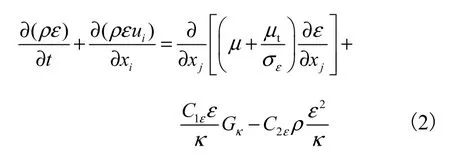
式中：ρ为流体密度；κ为湍动能；ui为速度分量；xi为坐标分量；μ为流体黏度系数；tμ为湍动黏度；Gκ是由于平均速度梯度引起的湍动能κ的产生项；ε为湍动耗散率；C1ε、C2ε为模型常数.

1.4网格对数值计算影响分析

为检验网格对计算的影响，对不同网格密度（网格总数为0.5×104～8.0×104）射流中心轴线的速度分布以及射流断面的速度分布进行了对比（如图5所示，其中ν 为射流流向平均速度，r为射流径向位置长度，x为距离射流出口的轴向距离）.从图5可以看出，随着网格数的减少，计算结果在核心区维持射流初始速度的能力降低，在核心区以后较长的一段距离内，小网格数下的速度显著小于密网格的计算结果，射流整体衰减较快.但在充分远处，粗网格与小尺度网格在射流中心轴线上的速度差距减小.同时，可看出采用标准κ-ε湍流模型的本算例在计算域中至少需要16×104以上网格数才能较准确反映出射流特征.

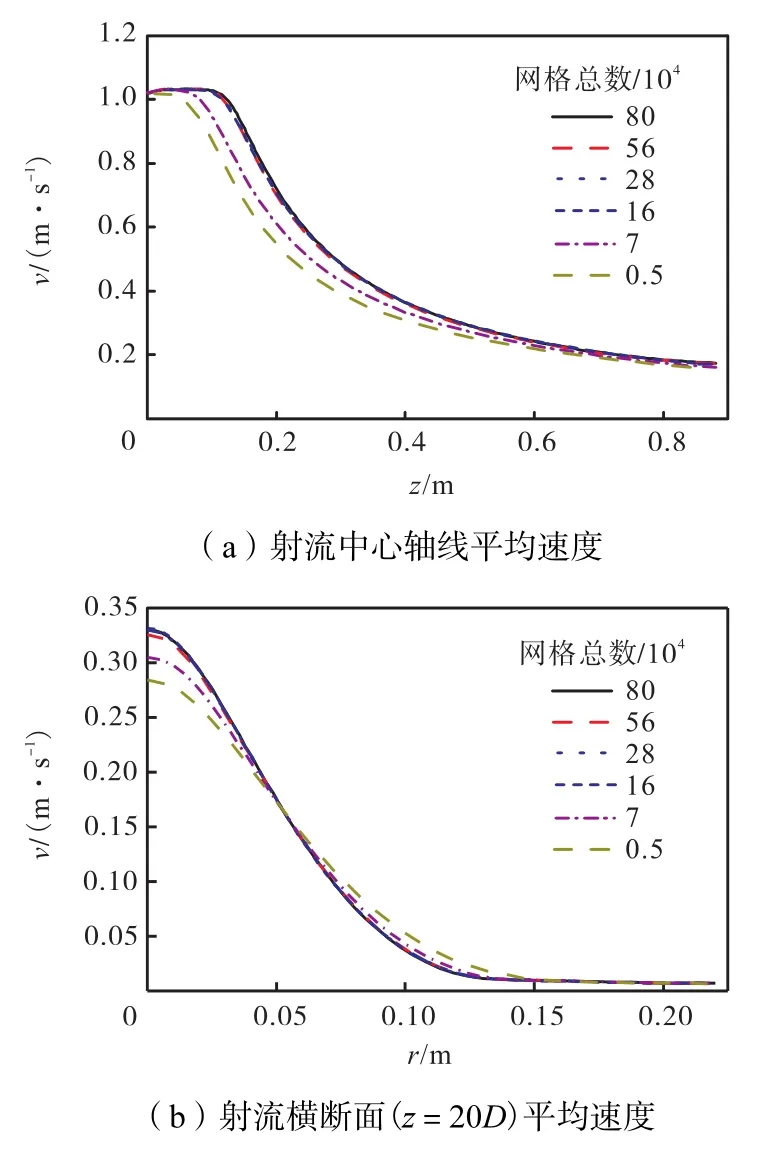
图5　不同网格下射流中心轴线与横断面的平均速度分布Fig.5Distribution of centerline axial average velocity and radial average velocity with different qrid cell number

网格数为0.5×104的情况下，最小网格尺度为0.004，m，大约为56×104网格下最小网格尺度的6倍.网格尺度的增大，使得模拟计算的网格数减少，由图5可知，网格数太少对计算结果在起始段和主体段将引起明显误差，故确定对网格数为56×104的计算结果与实验结果进行对比.图6为本文计算结果与Todde等［17］的实验结果在射流中心轴线的无量纲速度分布对比，无量纲化的速度表示为v∗，v∗=v/ v0，其中v为射流流向平均速度，v0为射流出口速度.可以看出，两者有非常好的吻合度.射流轴向的主流速度与实验整体符合很好，射流出口速度在核心区一直维持不变，在离开核心区后开始衰减，数值结果很好地反映了射流典型的流动特征.

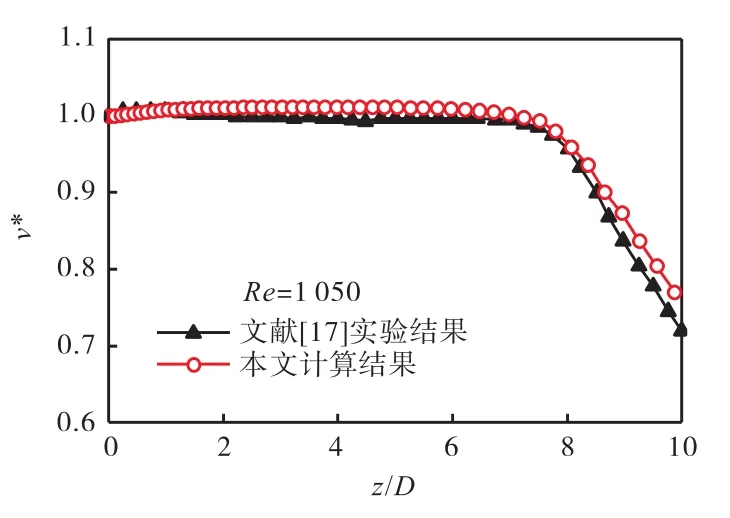
图6　射流出口区域中心轴线无量纲速度分布Fig.6 Dimensionless velocities of jet centerline in the exit region

湍射流的一个重要特点是在射流的主体段各截面流向时均速度分布具有相似性，即可用某一函数表示为

式中：vm为断面中心轴线上的流向最大时均速度；b12为射流半速度值宽度，其定义为v=vm/2时的r值.按网格点沿流向的分布规律取180层横截面，在60层（大约8D）以后发现流向速度具有自相似性（见图7）.

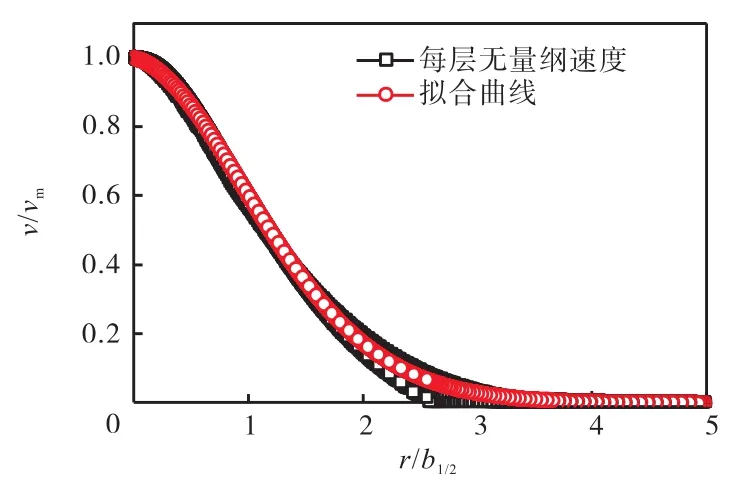
图7　无量纲流向时均速度分布Fig.7 Distribution of dimensionless streamwise mean velocity

2　耗散率修正κ-ε湍流模型

2.1数值耗散与耗散方程修正

由图5可见，当网格总数小于16×104时随着网格尺度的增大，射流沿径向和轴向衰减过快.为此图8进一步对比了不同网格数下射流核心区的长度占比（即大尺度与小尺度网格下射流核心区中心轴线长度之比），可明显看出，当网格总数减至0.5×104时射流刚刚出流就衰减了，此时核心区不复存在（即射流核心区长度占比为0）.这表明网格尺度的增大使得计算过程中数值耗散增大，射流在发展过程中耗散更快.因此，采用粗网格实施计算时，必须考虑对标准κ-ε湍流模型中的耗散方程进行修正，以便保证在粗网格情况下能够得到与小尺度网格（即较密网格）相同精度结果.

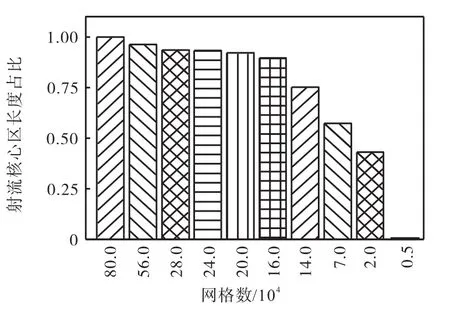
图8　不同网格数下射流核心区长度占比Fig.8 Length ratio of the jet core area in different meshes

在标准κ-ε湍流模型的耗散率方程中，认为湍动能耗散的生成、扩散以及消耗等项与湍动能方程中的对应项（即生成项、扩散项和耗散项）有类似的机制和公式，即

式中：A1为湍动能耗散率的生成项；B1为湍动能耗散的消耗项；C1为湍动能耗散的梯度扩散；υt为湍流运动黏度.C2ε由格栅湍流的衰减指数确定［18］. 均匀湍流的衰减符合幂函数率，湍动能与流程有幂次函数关系

由湍动能方程得

将式（5）、式（6）代入湍动能耗散方程，可得

由式（7）可知，随着n的减小，幂函数x-n-1的变化趋于缓慢，也就是耗散率ε的变化率变小，相应地，湍动能耗散率的耗散减小.n的减小意味着C2ε的增大，因此要减小因网格尺度增大引起的数值耗散增大必须对C2ε进行增大修正.

耗散方程式中系数C1ε是利用壁湍流和均匀剪切湍流的经典实验结果确定的［18］.利用壁湍流等应力区中湍动能耗散率的近似公式及均匀剪切湍流中k/ε趋于常数等条件，可以得到

式中P为湍动能生成项.由式（8）可看出，在计算中为了保证射流的耗散减小，在修正C2ε的同时C1ε也必须进行相应修正.将修正后的系数C1ε和C2ε分别表示为C1ε′和C2′ε，得到新的耗散率方程为

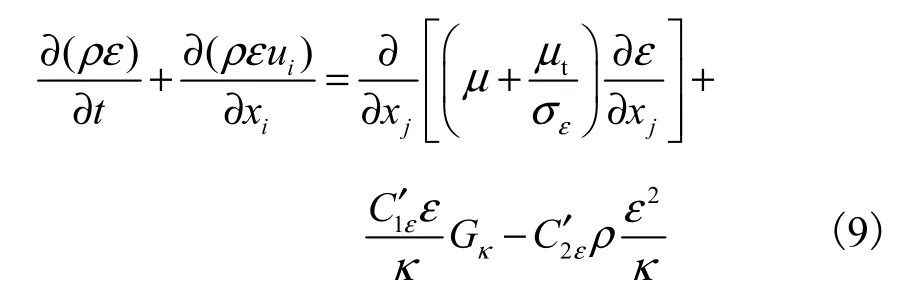
将式（9）与湍动能方程式（1）一起组成修正的κ方程和ε方程，参与湍流动量方程的计算.在计算中将通过修正湍流耗散率，纠正网格引起的过大数值耗散，提高计算结果的准确性.将修正后的湍流模型命名为耗散率修正κ-ε湍流模型（modified dissipation rate κ-ε turbulent model，MDR κ-ε）.本文中，原始系数值为C1ε=1.44，C2ε=1.92，经修正后的系数值为C1′ε=1.892，C2′ε=2.330.

2.2MDR κ-ε湍流模型验证

采用MDR κ-ε模型对本文圆射流计算结果进行对比.图9为采用MDR κ-ε模型0.5×104网格数与标准κ-ε模型56×104网格数的结果对比，两者在射流主体段有非常好的符合度，该区域正是机舱个性化送风口射流特征分析所关心的部分.从图10沿流向z=10D和z=20D两截面位置主流速度分布可以看到，沿径向速度分布及衰减变化与标准κ-ε模型56×104密网格的计算结果完全重合，表明MDR模型对粗网格的数值耗散进行了有效修正，适用于进行粗网格下圆射流的正确计算.

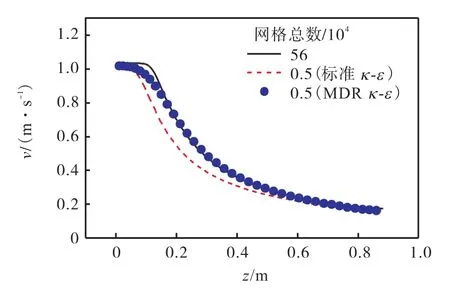
图9　射流中心轴线平均速度对比Fig.9 Comparison of mean velocity on jet centerline

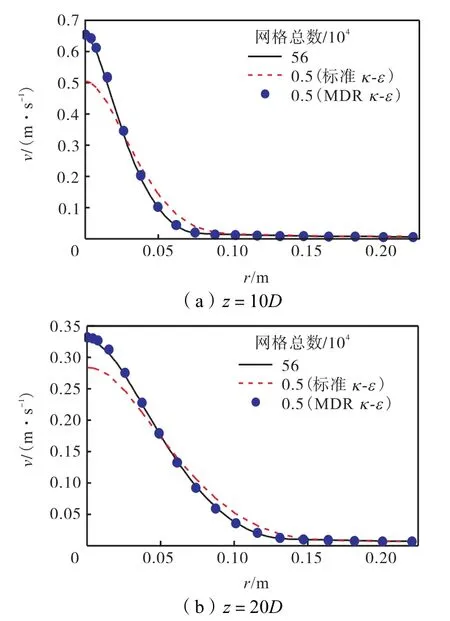
图10　射流横断面平均速度对比Fig.10Comparison of mean velocity on jet horizontal section

2.3不同雷诺数的适用性

考虑到个性送风口的出口速度在一定范围内变化，下一步验证侧重于验证不同出口速度下MDR，κ-ε湍流模型的适用性.个性化送风口的雷诺数在1，000～2，000之间，本文在Re=1000基础上，增加Re=1540和Re=2 040相同大网格尺度下的计算结果比较.图11为2种雷诺数下射流平均速度沿轴向分布，可看到速度的变化在核心区外完全与小尺度密网格下的结果比较相符.图12所示的射流平均速度沿径向分布对比表明两者吻合很好.

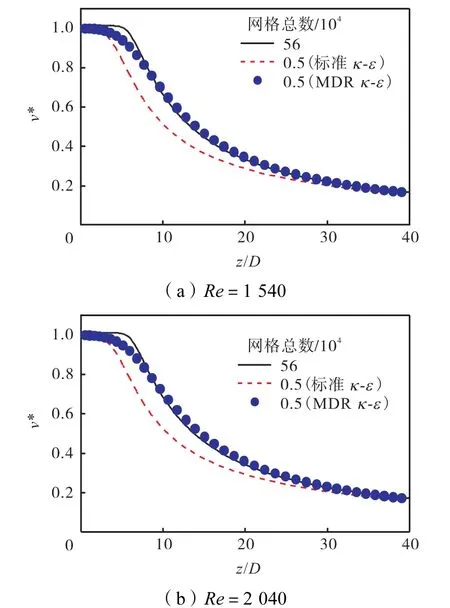
图11　不同雷诺数射流中心轴线平均速度对比Fig.11Comparison of mean velocity with different Reynolds numbers on jet centerline

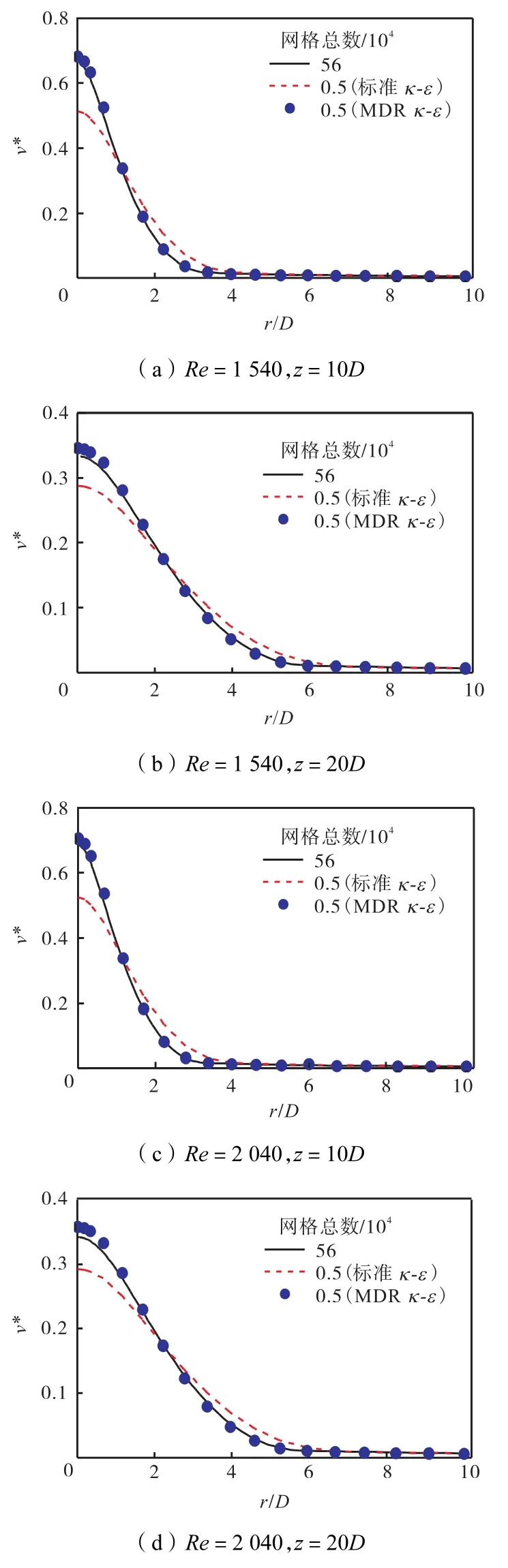
图12　不同雷诺数射流横断面平均速度对比Fig.12 Comparison of mean velocity with different Reynolds numbers on jet horizontal section

2.4非等温射流条件下MDR模型验证

实际机舱个性化通风调节中遇到的情况大多属于非等温湍流射流.座舱内送风温度约在18～29，℃［19］，为验证在非等温情况下MDR κ-ε湍流模型的适用性，本文进一步考察了温差为5，℃的典型工况.射流入口温度为20，℃，计算出口温度为25，℃，壁面为绝热壁面.从图13中心轴线平均速度和温度对比可以看出，不论是速度场还是温度场，其沿轴向的分布都较相同尺度网格下的标准κ-ε模型得到了有效修正，在核心区外与小尺度密网格结果具有高度一致性.

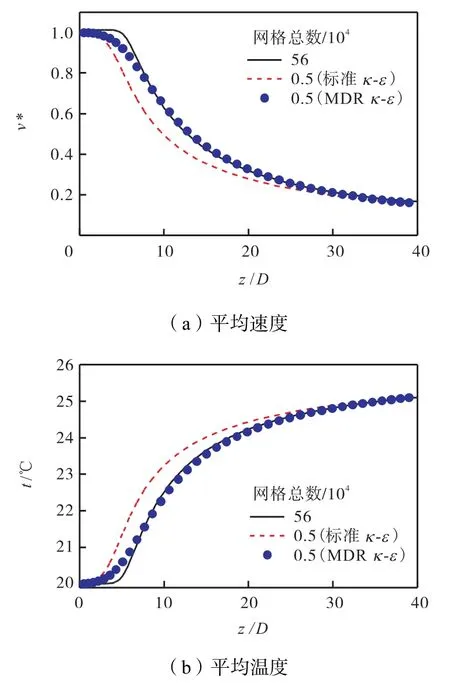
图13　非等温射流中心轴线平均速度与温度对比Fig.13Comparison of mean velocity and temperature on non-isothermal jet centerline

3　结 语

通过对基于机舱个性送风口的分析，以圆湍射流作为研究对象对比了标准κ-ε湍流模型在变网格尺度下的结果差别.在确定标准κ-ε湍流模型小尺度密网格计算结果与实验值吻合前提下，对由于网格尺度增大导致数值耗散过高，射流沿轴向和径向衰减过快问题，从湍流耗散率方程出发，通过对湍流耗散率生成项和耗散项与网格尺度关系的修正，获得修正的湍流模型，提高了粗网格下圆射流计算结果的精度.

采用修正后的MDR κ-ε湍流模型，验证了变雷诺数以及非等温条件下对射流流场数值计算，证明了修正模型的有效性和在机舱个性化送风口湍流特征计算中的适用性.

本文提出的基于粗网格的MDR模型避免了网格数目过大给计算带来的难度，使整舱大空间流域的气流特征及控制的正确和快速数值模拟成为可能.参考文献：

［1］Lippmann M，Burge H A，Jones B W，et al. The Airliner Cabin Environment and the Health of Passengers and Crew［M］. Washington：National Academy Press，2002.

［2］刘正先，张冀伸，平 艳. 机舱通风口冲击射流湍流特征分析及验证［J］. 天津大学学报：自然科学与工程技术版，2014，47（4）：292-297. Liu Zhengxian，Zhang Jishen，Ping Yan. Numerical analysis and verification of turbulent characteristics for the impinging jet flow in air vents of aircraft cabin［J］. Journal of Tianjin University：Science and Technology，2014，47（4）：292-297（in Chinese）.

［3］刘俊杰，李建民，李 斐，等. 大型客机座舱空调通风实验平台搭建及实验研究［J］. 天津大学学报：自然科学与工程技术版，2014，47（4）：283-291. Liu Junjie，Li Jianmin，Li Fei，et al. Establishment and experimental study of an air-conditioning ventilation experimental platform in a real full-size aircraft cabin［J］. Journal of Tianjin University：Science and Technology，2014，47（4）：283-291（in Chinese）.

［4］刘九五，连之伟，王月梅. CFD在暖通空调系统中的应用现状与发展［J］. 建筑热能通风空调，2010，29（6）：1-6. Liu Jiuwu，Lian Zhiwei，Wang Yuemei. Current applications and development of CFD simulations in HVAC system［J］. Building Energy & Environment，2010，29（6）：1-6（in Chinese）.

［5］赵 彬，李先庭，彦启森. 室内空气流动数值模拟的风口模型综述［J］. 暖通空调，2000，30（5）：33-37. Zhao Bin，Li Xianting，Yan Qisen. Review of air supply opening models in numerical simulation of indoor air flow［J］. HV & AC，2000，30（5）：33-37（in Chinese）.

［6］Nielsen P V. Flow in Air Conditioned Rooms［D］. Copenhagen：Technical University of Denmark，1974.

［7］Nielsen P V，Restivo A，Whitelaw J H. The velocity characteristics of ventilated rooms［J］. Journal of Fluids Engineering，1978，100（3）：291-298.

［8］Gosman A D，Nielsen P V，Restivo A. The flow properties of rooms with small ventilation openings［J］. Jour nal of Fluids Engineering，1980，102（3）：316-323.

［9］Huo Y，Haghighat F，Zhang S，et al. A systematic approach to describe the air terminal device CFD simulation for room air distribution analysis［J］. Building and Environment，2000，35（6）：563-576.

［10］Heikkinen J. Modeling of a supply air terminal for room air flow simulation［C］//Proceedings of the 12，th AIVC Conference on Air Movement and Ventilation. Ottawa，Canada，1991：213-230.

［11］Chen Q，Moser A. Simulation of a multiple-nozzle diffuser［C］// Proceedings of the 12，th AIVC Conference on Air Movement and Ventilation. Ottawa，Canada，1991：1-13.

［12］Emvin P，Davidson L. A numerical comparison of three inlet approximations of the diffuser in case E1 Annex 20［C］// Proceedings of ROOMVENT'96. Yokohama，Japan，1996：219-226.

［13］Nielsen P V. The description of supply openings in numerical models for room air distribution［J］. ASHRAE Transactions，1992，98（1）：963-971.

［14］Ferdman E，Oslash M V，T-Uacute，et al. Effect of initial velocity profile on the development of round jets［J］. Journal of Propulsion and Power，2000，16（4）：676-686.

［15］刘沛清. 自由紊动射流理论［M］. 北京：北京航空航天大学出版社，2008. Liu Peiqing. Theory of Free Turbulent Jet［M］. Beijing：Beihang University Press，2008（in Chinese）.

［16］张兆顺，崔桂香，许春晓. 湍流理论与模拟［M］. 北京：清华大学出版社，2005. Zhang Zhaoshun，Cui Guixiang，Xu Chunxiao. Theory and Modeling of Turbulence［M］. Beijing：Tsinghua University Press，2005（in Chinese）.

［17］Todde V，Spazzini P G，Sandberg M. Experimental analysis of low-Reynolds number free jets［J］. Experiments in Fluids，2009，47（2）：279-294.

［18］Launder B E，Spalding D B. The numerical computation of turbulent flows［J］. Computer Methods in Applied Mechanics and Engineering，1974，3（2）：269-289.

［19］Hunt E H，Reid D H，Space D R，et al. Commercial airliner environmental control system：Engineering aspects of cabin air quality［C］// The Aerospace Medical Association Annual Meeting. Anaheim，USA，1995：1-8.

（责任编辑：金顺爱，王晓燕）

Turbulence Model for Round Jet Flow Based on Modification of Grid Numerical Dissipation

Liu Zhengxian，Zhang Xiaoxing，Zhang Lijie，Luo Jisheng
（School of Mechanical Engineering，Tianjin University，Tianjin 300072，China）

Based on the personalized vents in aircraft cabin，the turbent flow of round jet was studied. The results of the numerical simulation using the standard κ-ε turbulence model with fine gird were compared with those of the experiment. Taking those comparison results as a point of departure，the analysis on the simulation results with coarse grids revealed that an increase in gird scale caused significant increase of dissipation and decline of velocity in jet flow along the axial and radial directions. This excessive decay of jet flow with coarse grids was resolved by modifying the turbulent dissipation rate of the generation and dissipation terms. The factors that cause an excessive decay were balanced. The modified dissipation rate κ-ε turbulent model was presented in this paper. The applicability of the modified model under different Reynolds numbers and non-isothermal conditions was also studied. The modified turbulence model was found to be capable of avoiding the demanding grid requirements for aircraft cabins and reducing total grid number significantly. The flow characteristics inside the cabin with complex structures and boundary conditions could be accurately simulated as well.

personalized air supply opening；numerical simulation；turbulence model；turbulent dissipation rate

O358

A

0493-2137（2015）12-1050-07

10.11784/tdxbz201409054

2014-09-22；

2014-11-16.

国家重点基础研究发展计划（973计划）资助项目（2012CB720101）；国家自然科学基金资助项目（51276125）.

刘正先（1969—），女，博士，副教授.

刘正先，zxliu@tju.edu.cn.

网络出版时间：2014-11-21. 网络出版地址：http://www.cnki.net/kcms/doi/10.11784/tdxbz201409054.html.