气动肌肉-气缸并联平台结构设计及位姿控制
2015-10-24陶国良
陶国良,左 赫,刘 昊
(1.浙江大学机械工程学系,浙江杭州310027)
气动肌肉-气缸并联平台结构设计及位姿控制
陶国良,左 赫,刘 昊
(1.浙江大学机械工程学系,浙江杭州310027)
为改进传统气缸驱动并联平台刚度低、难以控制的缺点,提出一种由3根气动肌肉和一个气缸混合驱动的并联平台.该平台具有横摇、纵摇、升沉3个方向上的自由度,其中由气缸控制的平台等效刚度控制系统和由3根气动肌肉控制的平台位姿控制系统自然分离,降低了控制器的设计难度.在对并联平台系统进行建模分析的基础上,采用气缸与气动肌肉控制相对独立的控制策略,针对气动肌肉强耦合、高度非线性的力学特性,设计一种自适应鲁棒控制器对并联平台的运动进行位姿控制.仿真结果表明,该控制器能够获得高精度的平台位姿轨迹跟踪控制效果,其中在线参数辨识部分能够对非线性模型补偿算法进行实时修正,同时控制器具有良好的鲁棒性.
气动肌肉;并联平台;结构设计;建模仿真;自适应控制;位姿控制
并联平台是由多个执行器对同一运动平台作用控制运动及位姿状态的机构,具有良好的刚度特性,在并联机床、机器人、定位与测量装置、模拟器和医疗、娱乐设备上得到了广泛的应用[1-2].气动并联平台具有成本低、清洁无污染、生物适应性好等优点,但也由于工作介质的弹性特性使得位姿控制精度往往不高[3].
气动肌肉是一种利用压缩气体的能量产生轴向拉力的力驱动器,可以近似等效于一个变原长变刚度的非线性弹簧装置[4].气动肌肉与传统的气动执行器相比具有较高的刚度特性和功率质量比,便于进行精确的位置控制[5],气动肌肉与生物肌肉相似的力学特性也意味着一定意义上的生物柔顺性[6].
本文设计了一种由气动肌肉和气缸混合驱动的新型并联平台,在对并联平台系统进行详细建模分析的基础上,设计了自适应鲁棒控制器对并联平台进行位姿控制,并在理论及仿真实验中对控制器有效性加以验证.
1 高精度并联平台设计
1.1 并联平台结构设计
本文所设计的气动肌肉和气缸混合驱动的并联平台,具有横摇、纵摇、升沉3个方向上的自由度.并联平台由一个气缸和3根气动肌肉耦合驱动,气缸对运动平台提供向上的支撑力,3根气动肌肉提供控制运动平台所需的转动力矩,并联平台结构及气路如图1、2所示.
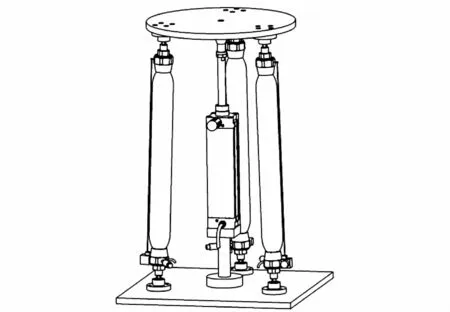
图1 并联平台结构示意图Fig.1 Schematic diagram of parallel platform structure
该机构除了具有其他并联平台的优点外,还具有以下特点:1)平台刚度由气缸独立控制,可实时调节平台的动态刚度,也可保持平台在运动过程中动态刚度相对不变.2)具有升沉、横摇、纵摇这3个应用最为广泛的自由度.3)可在首摇方向进行小范围自由运动,且气动肌肉与人体肌肉力学特性相似,具有生物柔顺性.4)并联平台结构对称,不仅具有准确的运动学逆解,也可得出较为准确的运动学近似正解,便于位姿解算器的设计和控制算法的应用.
该平台可以广泛应用于飞行模拟器、医疗设备、射电望远镜阵列和动感座椅娱乐设备等.

图2 并联平台气动系统示意图Fig.2 Pneumatic System of Parallel Platform
1.2 并联平台控制策略设计
该并联平台采用气缸与气动肌肉控制系统相对分离的控制策略,每根气动肌肉由一个正遮盖的电气比例方向阀进行控制,气缸则由一个高精度电气比例减压阀控制.并联平台的位姿控制部分仅对3个比例方向阀进行控制,而气缸输出力控制部分完成平台运行过程中保持气缸作用腔压力相对稳定的工作.由于运动平台在首摇方向上运动较小且难以测量,小范围首摇运动对平台其他自由度影响也较小,故不对平台在该自由度上运动进行测量及控制[7].
该控制策略具有以下优点:1)将气缸控制系统与气动肌肉控制系统分离,减小控制器设计难度.2)气缸输出力控制系统可以实时调节平台的动态刚度,并可将实际气缸作用腔压力作为位姿控制器的实时输入.3)并联平台位姿控制系统控制量为3个气动比例方向阀的控制输入,避免冗余控制量的产生.
2 高精度并联平台模型分析
2.1 并联平台运动学模型分析
运动平台共有3个转动自由度和一个移动自由度.取固定平台中心为坐标系0,移动平台中心为坐标系1.平台工作空间到关节空间状态变换公式如下:

式中:Li为第i根气动肌肉对应长度向量,Ri为第i根气动肌肉与固定平台铰接点在坐标系0中位置向量,r1i为第i根气动肌肉与运动平台铰接点在坐标系1中位置向量,z为运动平台沿z轴方向升沉高度,为坐标系1相对于坐标系0的旋转变换矩阵,如忽略平台绕z轴转动,其表达式如下:
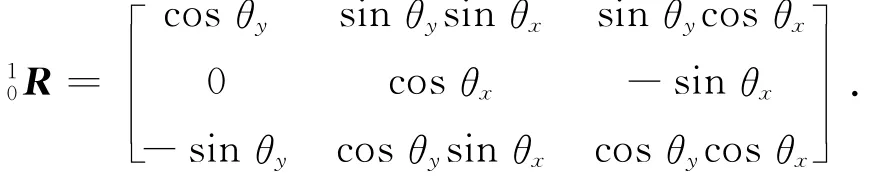
式中:θ为运动平台RPY转动角度,下标x表示绕x轴转动,下标y表示绕y轴转动.
2.2 并联平台动力学模型分析
首先对运动平台的转动运动学进行建模,对于运动平台的转动状态分析如下[8]:
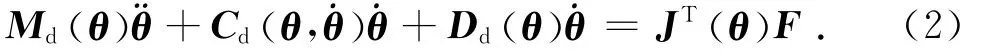
式中:Md(θ) 为运动平台的惯性项,Cd(θ,˙θ)为运动平台的哥式力项,Dd(θ) 为运动平台的阻尼项.
各项具体表达式如下:

式中:Gd(θ) 为运动平台的位姿RPY角度的导数到角速度之间的变换矩阵,I1(θ) 为运动平台在坐标系1上的转动惯量,为坐标变换后的角速度矩阵,J(θ) 为力矩计算矩阵,具体表达式为J(θ)=Jω(θ)Gd(θ),其中Jω(θ) 为移动平台坐标系1到固定平台坐标系0的力雅克比矩阵,F为气动肌肉产生的拉力向量,CS为铰链库伦摩擦系数对角矩阵.
运动平台在竖直方向上受力分析如下:
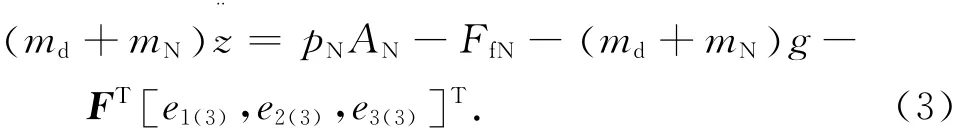
式中:md为运动平台质量,mN为气缸活塞及连接件质量,pN为气缸作用腔压力,AN为气缸作用腔活塞面积,FfN为气缸活塞所受摩擦力,g为重力加速度,ei(3)为气动肌肉拉力方向单位向量的竖直分量,下标i表示第i根气动肌肉.
2.3 气动肌肉输出力模型分析
气动肌肉的力学分析采用如下的非线性气动肌肉力-压力-位移模型[9-10]:

其中:

式中:a、b为气动肌肉结构所决定的参数,p为气动肌肉内腔压力,ke为气动肌肉2个端头非圆柱部分的体积修正系数,ε为气动肌肉收缩率,Sc为等效摩擦作用面积,fs为气动肌肉摩擦系数,x为气动肌肉运动过程中的收缩量,α为气动肌肉纤维编织网夹角,下标0表示气动肌肉初始状态,D为气动肌肉内径,L为气动肌肉长度,tk为橡胶套筒橡胶层厚度,E为橡胶弹性模量,kFri为修正系数.
在实际应用中,气动肌肉的模型更为复杂,影响因素较多,且具有慢时变特性,故需要加入自适应参数辨识算法对气动肌肉的力学模型进行在线辨识及补偿.
2.4 气缸输出力模型分析
气缸对运动平台的中心起支撑作用,其无杆腔的压力由Festo公司MPPES比例减压阀控制.首先根据所需的平台刚度特性选定比例减压阀设定值,在平台运行过程中该设定值不会发生改变,且在阀口与气缸之间增加适当容积的气容以稳定气缸无杆腔内气压.根据气缸最大运行速度选用合适型号的比例减压阀,以保证平台运行过程中气缸无杆腔压力的基本稳定.由于气缸无杆腔压力会被传感器测量,并被传递至之后的控制器中进行补偿,故小范围的压力变化对控制效果影响不大.
假设气缸无杆腔内部气压与比例减压阀的模拟量设定值呈线性关系,公式如下所示:

式中:uN为比例减压阀的设定量,pN0为比例减压阀下游压力与设定量之间的比例关系.
气缸摩擦力的机理较为复杂,先后有许多静态及动态模型被广大学者提出并采用.其中Stribeck静态模型结构较为简单,不需要对摩擦力内部状态进行动态分析,且能较为完整地反应气缸摩擦力的各项特性,故使用Stribeck模型对气缸摩擦力进行描述,模型如下[11]:
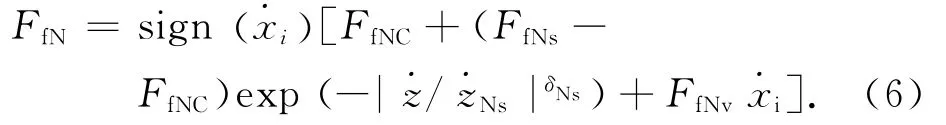
式中:FfNs为最大静摩擦力,FfNC为库伦动摩擦力, FfNv为黏性摩擦力系数,为局部极值点对应速度,δNs为Stribeck曲线系数.
2.5 气动肌肉压力模型分析
将气动肌肉内腔气体压力变化过程近似为多变过程,以矩阵方式表示出来如下[12]:


式中:qm为通过比例方向阀质量流量,λ为多变指数,其值在1至1.4之间,p0为标准状态下大气压力,R为标准状态下气体常量,T为环境绝对温度, Vi、为气动肌肉内腔体积及体积变化率.
2.6 比例方向阀流量模型分析
使用如下流量方程对气体通过比例方向阀的流量特性进行建模[13]:

式中:p、T分别为气体压力及温度,下标u表示阀口上游,下标d表示阀口下游,γ为标况下气体的比热比,空气为1.4,Ae为比例方向阀的等效节流面积.
所使用的比例方向阀为Festo公司MYPE系列正遮盖比例方向阀,在中位具有死区,非死区部分线性度较好,故使用如下模型对比例方向阀等效节流面积进行建模[14-15]:

式中:Ae0为等效节流面积比例系数,uu为充气通路连通时的最小电压,ul为放气通路连通时的最大电压,负值表示气动肌肉处于排气状态.
2.7 模型仿真结果
由第2章模型分析结果可以看出,本课题所研究气缸-气动肌肉并联平台系统模型具有以下特点:1)模型复杂且包含大量难以求导的三角函数、非整数次乘方和有限平滑函数,不利于进行在此基础上的大量计算(如求解雅克比矩阵、求解全微分方程等);2)模型具有很强的非线性特性,在工作点附近进行一次泰勒展开并不能很好地表现系统的动力学特性;3)模型中各状态量相互耦合,运动平台的受力与气动肌肉内腔压力和平台位姿均密切相关,气体动态过程和平台运动过程不能相互分离;4)气动肌肉和气缸的输出力平衡决定并联平台的最终平衡位姿,气缸输出力的大小决定系统内部耦合力的强弱和平台的动态刚度,气动肌肉内腔体积及其控制阀等效面积的关系是限制并联平台位姿运动速度的最重要因素.
根据第2章所得结果利用simulink工具箱对并联平台进行系统建模仿真,部分关键仿真参数如表1所示.
对并联平台模型进行开环信号仿真实验.取3个比例方向阀的控制信号为在1、2、3 s时产生0到1的阶跃信号,并联平台及气动肌肉仿真结果如图3所示,改变比例压力阀的设定值,并调节气动肌肉内腔压力使得平台在初始状态时处于同一高度上.在0.5 s时刻引入对运动平台竖直向下的100 N的干扰力,从而测试平台刚度对平台抗干扰能力造成的影响.平台运动仿真结果如图4所示.

表1 并联平台关键仿真参数Tab.1 Key Simulation Parameters of Parallel Platform
从运动仿真结果可以看出,增大气缸作用腔压力可以提高并联平台整体刚度,在相同干扰作用下刚度越高平台进入稳定状态所需时间就越短,造成的稳态影响也越小.但气缸作用腔压力的提高会带来并联平台内部各铰接点作用力的上升,实际运行过程中可能会引起铰接点摩擦力的增加,同时气缸作用腔压力的一部分还要作为运动平台负载的支撑力,故应根据实际需要合理设定气缸作用腔压力.
3 高精度并联平台控制器设计
3.1 基于反步法的ARC控制器设计及收敛性证明
由于气动肌肉具有复杂的力-位移-压力特性,基于模型线性化补偿的控制策略容易引入较大的模型补偿误差,线性化后的模型与实际模型也有较大差距,难以获得较好的控制效果.针对气动肌肉强耦合、高度非线性的力学特性,本文采用反步法设计基于非线性模型的自适应鲁棒控制策略(ARC)[16],在工作空间中对运动平台进行高精度位姿控制.
步骤1:
设定系统状态量为X=[θx,θy,z]T,忽略运动平台绕z轴运动带来的影响,将气缸-气动肌肉并联平台动力学模型写为矩阵微分形式:

式中:A为运动平台动力学惯性矩阵,fX( X)为模型已知非线性部分,
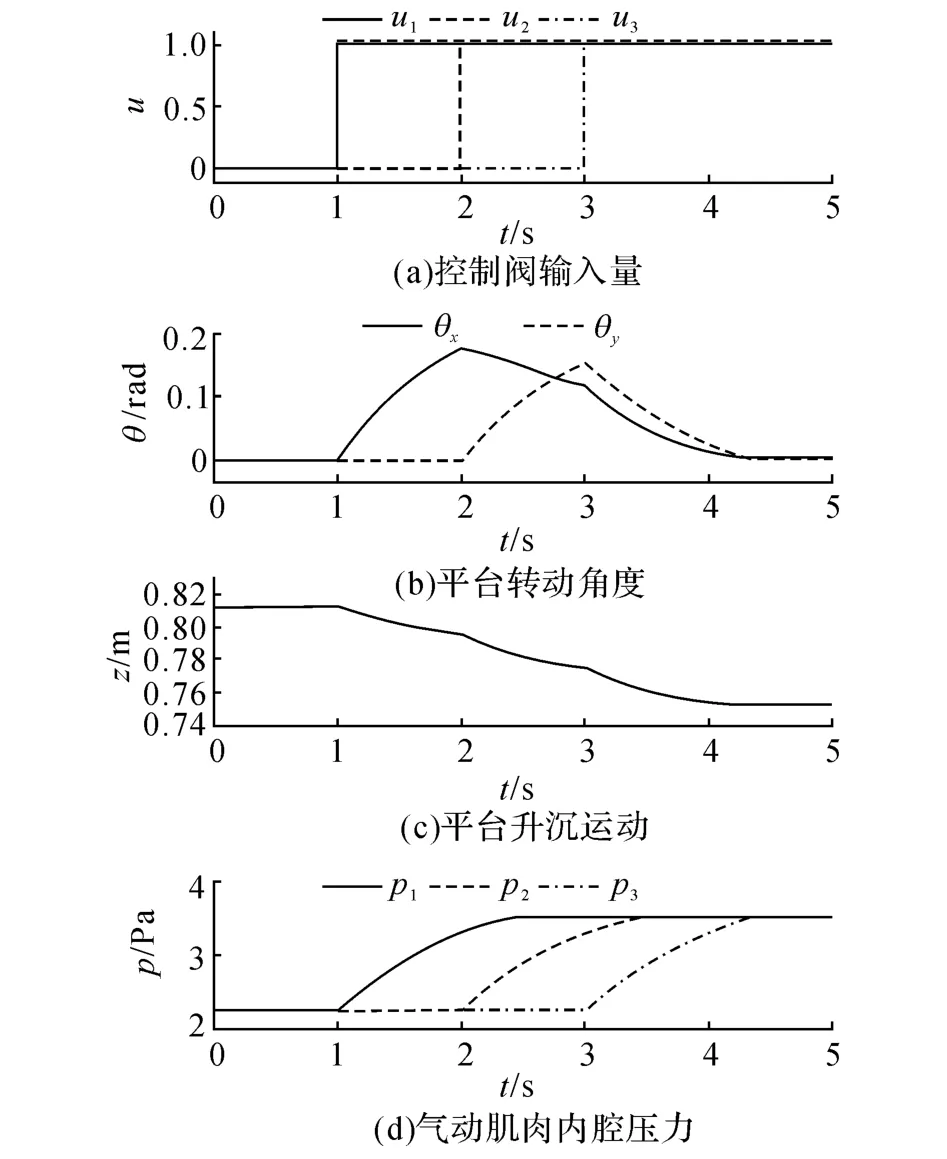
图3 阶跃信号仿真结果Fig.3 Simulation of Step Signal Input
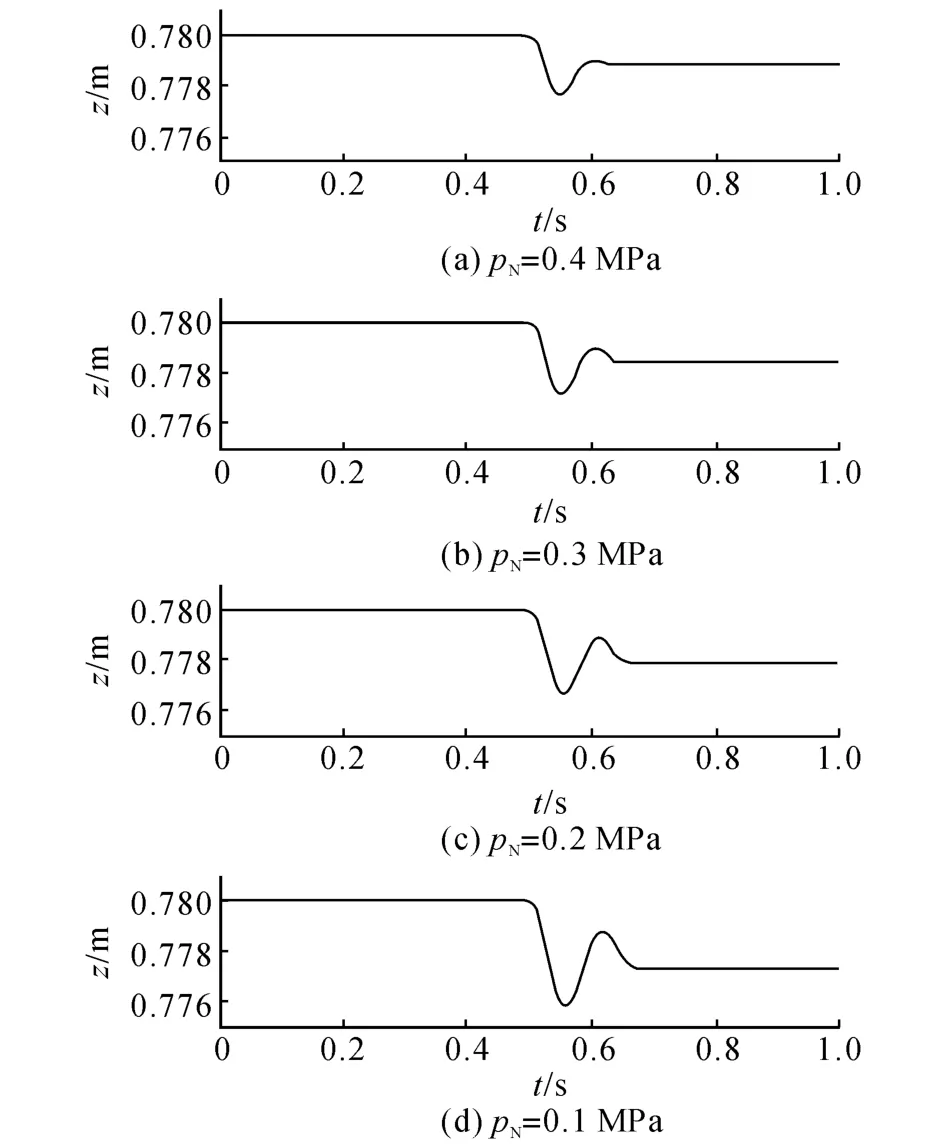
图4 不同刚度平台受外力干扰运动仿真Fig.4 Motion Simulation of Platform in Different Stiffness under Force Disturbance
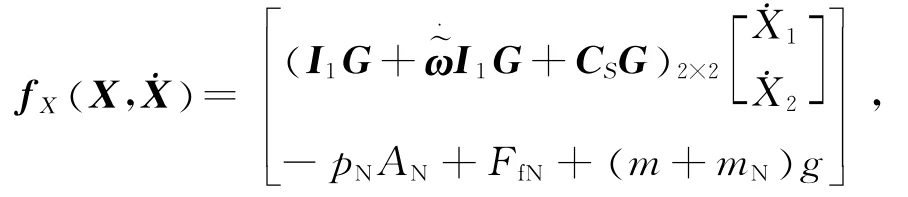
设Xd为期望状态量,Z1=Xd-X为状态量控制误差;Z2=+KSZ1,由Z1到Z2的传递函数可知,当Z2收敛于零时,Z1也收敛于零.
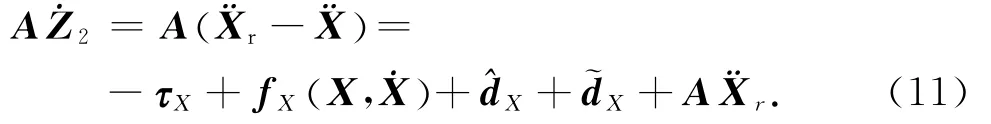
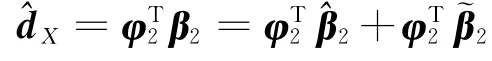
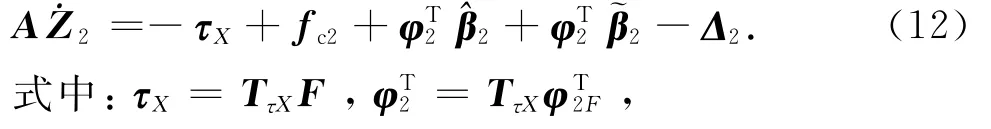
其中,TτX为气动肌肉力矩转换矩阵.根据气动肌肉力学特点,选择如下自适应参数矩阵:

对于自适应参数估计部分,为保持参数估计始终有界,采用如下的非连续参数投影算法:


设理想等效输入力矩如下:
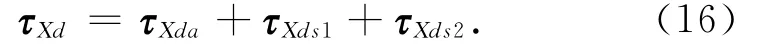
式中:τXda为非线性部分补偿量,τXds1为保证系统处于切换层内部时的稳定收敛性,τXds2为保证系统鲁棒性的模型不确定抑制量,应满足

公式(16)中各部分表达式如下:

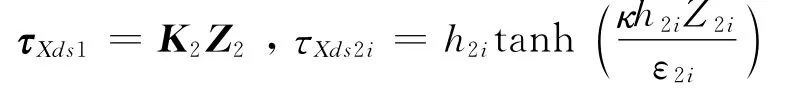
取半负定李雅普诺夫函数:
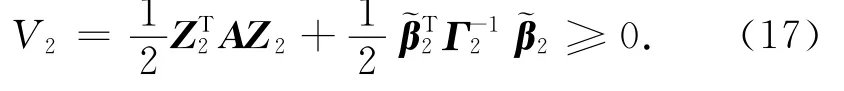
则有

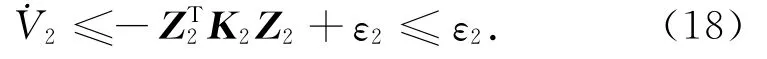
此时,Z2将会以指数方式收敛于半径以ε2相关的球域内,使得系统误差有界.
步骤2:

式中:Fd为气动肌肉理想输出力向量.
将符号函数做连续化处理:
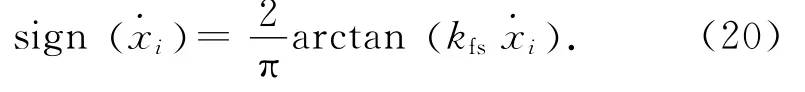
根据式(7),压力层模型为

式中:τp=fp(x) q为等效输入流量,为模型误差及外界干扰.
设pd为期望气动肌肉内部气体压力,Z3=pd-p为压力控制误差,则有


则式(22)变为

设fc3=˙pdc-gp,Δ3=p-˙pdu,则式(24)变为

设理想等效输入压力如下:

式中:τpda为非线性部分补偿量,τpds1保证系统处于切换层内部时的稳定收敛性,τpds2为保证系统鲁棒性的模型不确定抑制量,应满足

各部分表达式如下:

设半负定李雅普诺夫函数

则有
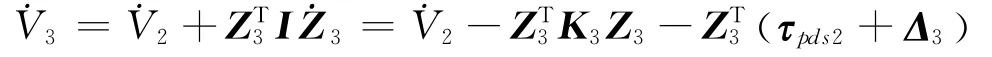
根据以上不等式可得
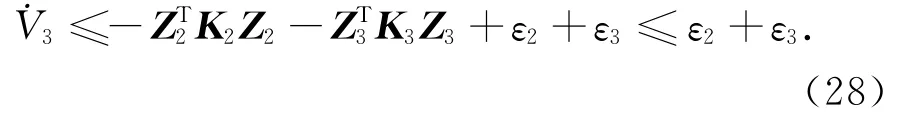
此时,Z2和Z3将指数收敛于一定的与ε2和ε3相关的球域内,从而证明此控制算法可保证并联平台系统稳定性.
根据式(4)、(8)可以反求理想等效节流面积:
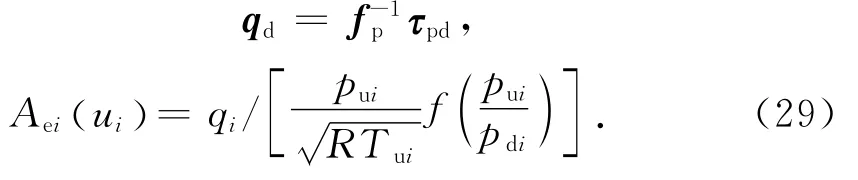
得出理想等效节流面积后,再根据比例方向阀死区特性式(9),对死区采用如下补偿算法后即可计算控制输出u:
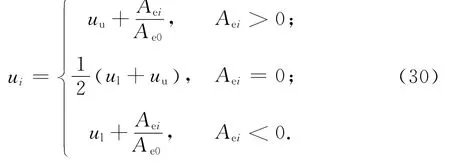
3.2 位姿跟踪控制仿真实验
在第2章所建立模型中对该算法的有效性进行验证.选取8 s为周期的正弦横摇信号与10 s为周期的正弦升沉信号组成的复合信号作为运动平台目标运动轨迹,进行运动平台的多自由度位姿跟踪控制仿真实验.实验中辨识参数的初值设定分别为30、15、5,在20 s时开始进行自适应参数辨识,仿真实验结果如图5所示.可以看到当自适应参数辨识部分起作用时,运动平台的跟踪误差明显减小.
在50 s时引入作用于运动平台中心竖直向下的100 N的力作为干扰,并在60 s时去掉干扰力,运动平台仅在干扰力发生变化的时刻发生少许振动,并在控制算法的作用下迅速恢复稳定.仿真实验结果如图6所示.
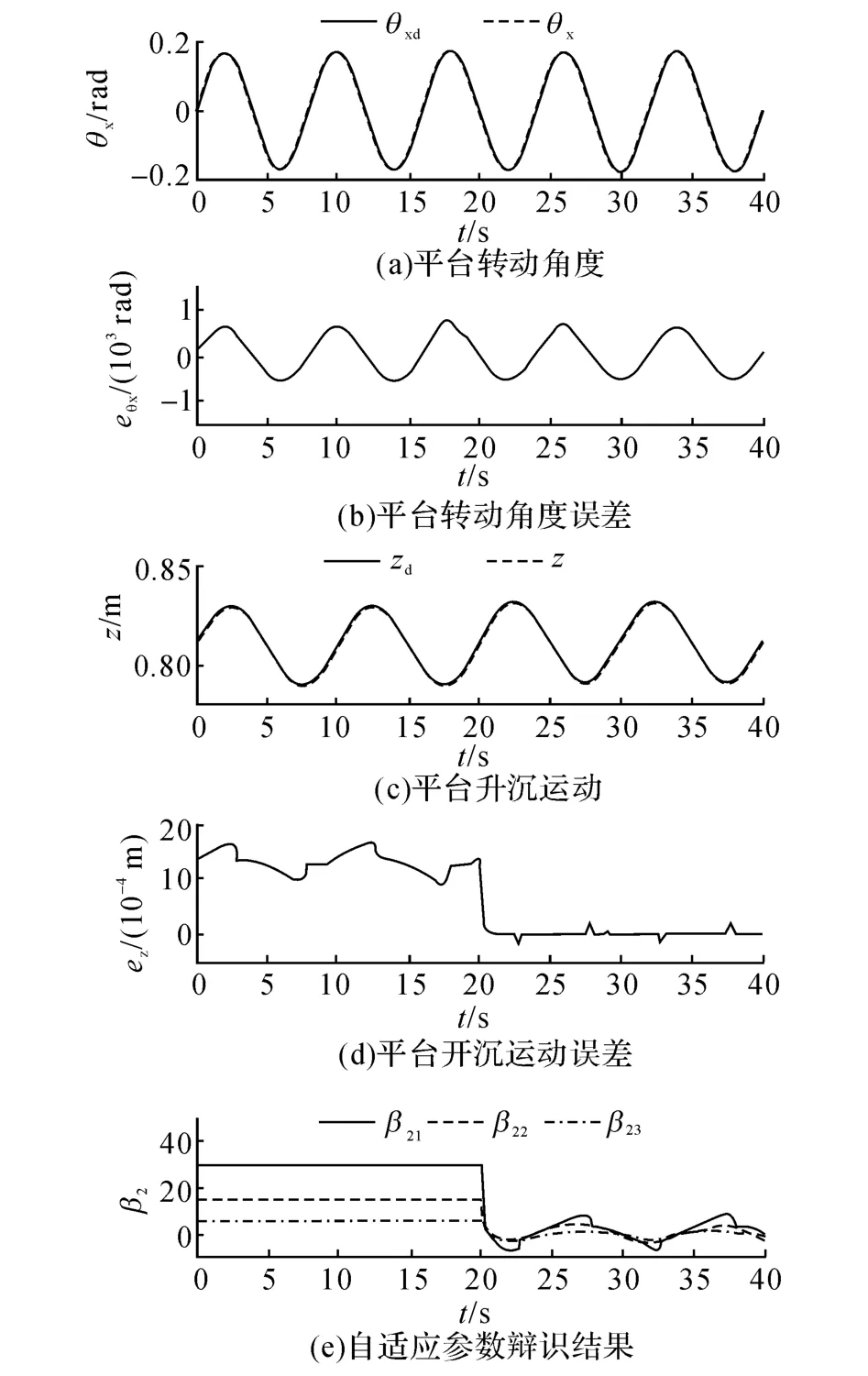
图5 DARC控制策略仿真试验结果Fig.5 Simulation of DARC Control Strategy
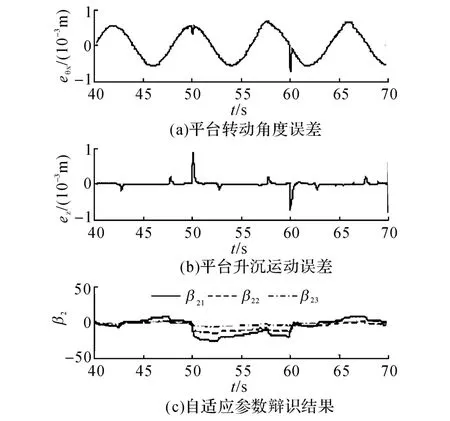
图6 控制鲁棒性仿真试验结果Fig.6 Simulation of Control Robustness
由仿真实验结果可以得出,所设计的DARC平台位姿控制器具有以下特点:
1)控制精度较高,稳定状态下各自由度最大位姿误差均小于1%;
2)能够实时辨识平台参数,并利用辨识结果改善平台位姿控制效果;
3)控制器对外界干扰不敏感,在引入干扰后能够迅速完成干扰量的辨识和控制器的镇定;
4)与图3所示开环仿真结果对比可以看出该控制算法中的气缸摩擦力补偿部分具有较好的运动平台振动抑制作用.
4 结 语
本文设计了一种新型三自由度气动肌肉-气缸并联平台,由比例减压阀控制气缸作用腔压力,3个比例方向阀控制3根气动肌肉长度及内腔压力.该平台采用气动肌肉与气缸相对分离的控制策略,在运行过程中可保持平台刚度相对稳定,与传统气缸驱动并联平台相比具有刚度高、控制简便等优点.在对并联平台进行建模研究及刚度特性研究的基础上设计了自适应鲁棒控制器,并完成了对该控制器的理论稳定性证明.仿真实验表明该控制器能够很好地进行高精度平台位姿轨迹跟踪控制,并且具有实时参数在线辨识能力和控制鲁棒性.在完成实验台搭建工作后,下一步研究重点应为将所设计自适应鲁棒控制器实现后作用于并联平台上,进行位姿轨迹跟踪控制实验并观测控制器实际控制效果.
(Reference):
[1]MENG Wei,ZHOU Zu-de,LIU Quan,et al.A practical fuzzy adaptive control strategy for multi-DOF parallel robot[C]//Proceedings of the 2nd International Symposium on Computer,Communication,Control and Automation(ISCCCA-13).Paris:Atlantis Press,2013:620 -623.
[2]DASGUPTA B,MRUTHYUNJAYA T S.The Stewart platform manipulator:A review[J].Mechanism and Machine Theory,2000,35:15-40.
[3]武卫,王占林.基于小脑模型神经网络的气动六自由度并联平台的复合控制方法研究[J].机械科学与技术.2008,27(6):748-751.
WU Wei,WANG Zhan-lin.A compound control method for a six-DOF parallel pneumatic manipulator based on CMAC networks[J].Mechanical Science and Technology for Aerospace Engineering,2008,27(6):748-751.
[4]傅晓云,方敏,李宝仁.气动人工肌肉刚度特性的分析[J].机床与液压,2007,35(2):109-111.
FU Xiao-yun,FANG Min,LI Bao-ren.Theoretic analysis of stiffness characteristics of the pneumatic muscle actuator[J].Machine Tool&Hydraulics,2007,35(2):109-111.
[5]施光林,沈伟.气动人工肌肉并联平台自适应模糊CMAC姿态跟踪控制[J].中国机械工程,2012,23(2):171-176.
SHI Guang-lin,SHEN Wei.Adaptive fuzzy CMAC position tracking control of parallel platform based on pneumatic artificial muscles[J].China Mechanical Engineering,2012,23(2):171-176.
[6]JAMWAL P K,XIE Sheng-quan,AW K C.Design analysis of a pneumatic muscle driven wearable parallel robot for anlde joint rehabilitation[C]//Mechatronics and Embedded Systems and Applications(MESA).Qingdao:IEEE,2010:403-408.
[7]TAO Guo-liang,ZHU Xiao-cong,YAO Bin,et al.A-daptive robust posture control of a pneumatic muscles driven parallel manipulator with redundancy[C]//Proceedings of the 2007 American Control Conference.New York City,USA:IEEE,2007:3409-3413.
[8]朱笑丛,陶国良.气动人工肌肉伺服平台的建模.浙江大学学报:工学版[J],2004,38(8):1056-1060.
ZHU Xiao-cong,TAO Guo-liang.Modeling of a servo platform driven by pneumatic artificial muscles[J].Journal of Zhejiang University:Engineering Science, 2004,38(8):1056-1060.
[9]TONDU B,LOPEZ P.Modeling and control of Mc K-ibben artificial muscle robot actuators[J].Journal of Dynamic Systems,Measurement,and Control,2000,122(3):416.
[10]ZUO He,TAO Guo-liang,ZHU Xiao-cong.Modeling and enhancement of Mc Kibben pneumatic muscle actuators[J].Advanced Materials Research,2012,591-593:793-796.
[11]ANDRIGHETTO P L,VALDIERO A C,CARLOTTO L.Study of the friction behavior in industrial pneumatic actuators[J].ABCM Symposium Series in Mechatronics,2006,2(2):369-376.
[12]RICHER E,HURMUZLU Y.A high performance pneumatic force actuator system Part I-Nonlinear mathematical model[J].Issue of ASME Journal of Dynamic Systems Measurement and Control,2000,122(3):416-425.
[13]JAMES E B,BRIAN W M.Modeling,identification, and control of a pneumatically actuated,force controllable robot[J].IEEE Transactions on Robotics and Automation,1998,14(5):732-742.
[14]OLABY O,BRUN X,SESMAT S,et al.Characterization and modeling of a proportional valve for control synthesis[C]//Proceedings of the 6th JFPS International Symposium on Fluid Power.Tsukuba,Japan:Japan Fluid Power System Society,2005:772-76.
[15]孔祥臻,刘延俊,王勇等.气动比例阀的死区补偿与仿真.山东大学学报:工学版[J].2006,36(1):99-102.
KONG Xiang-zhen,LIU Yan-jun,WANG Yong,et al.Compensation and simulation for the deadband of the pneumatic proportional valve.Journal of Shandong University:Engineering Science[J].2006,36(1):99-102.
[16]YAO Bin,TOMIZUKA M.Adaptive robust control of MIMO nonlinear systems in semi-strict feedback forms[J].Automatica,2001,37:1305-1321.
Structure design and motion control of parallel platform driven by pneumatic muscles and air cylinder
TAO Guo-liang,ZUO He,LIU Hao
(1.Department of Zhejiang University,Hangzhou 310027,China)
In order to overcome the shortcomings of platforms driven by air cylinders such as low stiffness and controlling complexity,a parallel platform driven by three pneumatic muscles and one air cylinder was designed.The platform had three degrees of freedom,namely roll,pitch and heave.The stiffness of the parallel platform was controlled only by the air cylinder,while the posture was controlled by three pneumatic muscles,so the controller could be easily designed separately.Based on the modeling analysis of the parallel platform,a control strategy which separately controlled the air cylinder and pneumatic muscles was employed.To overcome the limitation caused by the coupling and nonlinear characteristics of pneumatic muscles,an adaptive robust controller(ARC)was designed for posture controlling of the parallel pneumatic platform.Simulation results show that the proposed ARC controller can achieve a high level of precision of trajectory tracking motion control.With the ability of online parameter identification,the ARC controller is able to modify the nonlinear compensation part based on the identification results.The robustness of the ARC controller is also verified in simulation experiments.
pneumatic muscle;parallel platform;structure design;modeling and simulation;adaptive control;posture control
10.3785/j.issn.1008-973X.2015.05.002
TP 273;TH 138
A
1008-973X(2015)05-0821-08
2014-03-12. 浙江大学学报(工学版)网址:www.journals.zju.edu.cn/eng
国家自然科学基金资助项目(51375430).
陶国良(1964-),男,教授,博导,主要从事气动电子技术、气动伺服控制、工业自动化控制和测试、燃料电池、空气压缩机及压缩空气气动发动机等领域的研究.E-mail:gltao@zju.edu.cn
