数控机床旋转轴转角定位误差测量方法
2015-10-24何振亚傅建中徐月同
何振亚,傅建中,徐月同
(1.浙江大学机械工程学院,浙江杭州310027;2.华南理工大学机械与汽车工程学院,广东广州510640)
数控机床旋转轴转角定位误差测量方法
何振亚1,2,傅建中1,徐月同1
(1.浙江大学机械工程学院,浙江杭州310027;2.华南理工大学机械与汽车工程学院,广东广州510640)
为实现多轴数控机床空间误差的补偿,提出一种基于球杆仪组合路径的数控机床旋转轴转角定位误差的测量方法.根据转角定位误差敏感方向,通过组合切线测量和平动轴圆轨迹测量方法,无需机床空间误差模型和繁琐的误差解耦计算,便可直接辨识转角定位误差.采用模型仿真验证该方法的可行性和对照实验验证可靠性.实验结果表明组合路径测量方法的辨识结果与激光测量结果吻合较好,两者的测量结果差异δ≤0.007 8°.该方法测量过程操作简单、辨识原理直观易懂,可用于机床旋转轴定位精度的评估以及为误差补偿提供依据,从而提高机床加工精度.
旋转轴;转角定位误差;组合路径;球杆仪;数控机床
随着现代制造业的发展,多轴数控机床广泛应用于汽车、医疗、航空航天等先进装备制造领域[1].多轴数控机床是在传统的三轴机床的基础上增加旋转轴,因而多轴数控机床误差补偿控制更为复杂,不仅要考虑平动轴的运动误差,还需考虑旋转轴的运动误差.目前,对平动轴的运动误差研究已趋成熟,且在ISO230有明确的规定,但关于旋转轴的运动误差的研究却停留在探索阶段.
围绕多轴机床的空间误差测量课题,Lei等[2]开发了一种3D探针装置,专门测量五轴机床的空间误差.此方法需要规划特殊测量路径和结合空间误差模型进行误差解耦求解;Tsutsumi等[3-4]提出采用球杆仪对五轴机床的13个链接误差进行辨识,其中包括8个关于旋转轴的误差;Mayer等[5]提出采用球杆仪五步测量,并结合误差模型辨识各项误差,并开发了3D杯状传感器评估旋转轴的8个链接误差,但未包括转角定位误差[6].Zhu等[7]采用球杆仪测量旋转轴6项基本误差;张大卫等[8]提出采用球杆仪对机床旋转轴的4项误差进行检测,但未提及如何测量转角定位误差.Lee等[9]把旋转轴误差分为2大类:跟位置有关的误差以及跟位置无关的误差,并提出各项误差以及安装误差的估算方法,但也未提及转角定位误差的估算.前述所有基于球杆仪的误差测量方法,均须结合机床空间误差模型,进行误差解耦辨识,其辨识原理抽象,过程较复杂、易错.
李郝林等[10]提出利用标准球及红外三维工件测头对机床回转工作台转角误差进行测量,但测量精度受旋转运动的转角误差和主轴运动误差的耦合误差影响;梁军等[11]采用激光角度干涉仪实现了数控转台位置精度的测量.测量安装时,步进电机与被测转台回转中心需同轴安装,增加了安装难度,此外激光干涉仪和步进电机成本较高.
鉴此,本文提出一种低成本的基于球杆仪的机床旋转轴转角定位误差测量新方法,即组合路径测量方法(combined paths measurement method, CPMM).根据转角定位误差的敏感方向,采用球杆仪切线测量方法对旋转轴进行测量;同时,为了减小机床其他运动轴运动误差对被测旋转轴的影响,运用平动轴圆轨迹测量结果对切线测量数据进行修正,避免了误差解耦的繁琐过程,通过简单的代数计算可直接求解转角定位误差.最后采用模型仿真和高精度的激光测量对照实验验证CPMM的可行性和可靠性.
1 球杆仪典型运动测量原理
球杆仪广泛应用于评价和诊断数控机床动态精度[12].其工作原理是将球杆仪的两端分别安装在机床主轴与工作台上,测量两轴插补圆轨迹运动,通过分析测量轨迹与标准轨迹进行对比,从而评价机床精度,如垂直度、直线度、反向间隙、圆度和伺服比例不匹配等.
随着多轴机床的应用,球杆仪测量轨迹向多样化发展,如3个平动轴的空间测量、旋转轴的径向测量和轴向测量、三轴插补切向测量、圆环轨迹测量和球面轨迹测量等.测量时,机床运动需确保球杆仪两端安装球座的理想距离等于球杆仪的杆长.如图1所示,球杆仪的典型测量运动轨迹.如图1(f)所示,切线测量时,旋转轴的旋转运动以及与其垂直的2个平动轴平面圆轨迹运动构成的球杆两端圆环轨迹,并且球杆杆长方向始终相切于内圆,故命名为球杆仪切线测量.

图1 球杆仪的典型测量运动轨迹Fig.1 Typical paths of ball bar measurement
2 组合路径测量方法
采用球杆仪对机床旋转轴转角定位误差进行检测.根据转角定位误差的敏感方向为切线方向,采用球杆仪的切线测量路径.切线测量时机床2个平动轴和一个旋转轴三轴联动,因此切线测量结果反映的是三轴运动的耦合误差.传统的辨识方法是根据传递矩阵的机床空间误差模型解耦计算,最后分离出转角定位误差.为了避免传统方法导致的繁琐空间误差解耦辨识过程,本文提出采用CPMM,即组合切线测量和平动轴圆轨迹测量,对机床旋转轴转角定位误差进行测量和辨识.
测量原理:通过平动轴圆轨迹测量数据,分解出平动轴圆轨迹运动产生的误差对切线方向的影响分量.然后,用此分量修正切线测量结果,从而巧妙地解决了球杆仪测量时多轴运动带来的误差解耦问题,简化了转角定位误差求解过程.
以C轴为例介绍CPMM原理.如图2所示,球杆仪C轴的切线测量示意图.测量轨迹由X、Y轴插补圆轨迹运动,以及C轴的旋转运动形成.因此,在切线方向(杆长方向)不仅受C轴转角定位误差的影响,也受X、Y两轴插补圆轨迹运动所产生的误差的影响.如图3所示,X和Y轴的插补圆轨迹测量.圆轨迹的圆心,设置在C轴的旋转中心上,并且杆长|ON′|=|ON|,即如图3所示的N′点轨迹与图2所示的N点轨迹是相同的.

图2 球杆仪C轴切线测量Fig.2 C-axis tangential measurement of ball bar

图3 X和Y轴的平面圆轨迹测量Fig.3 X-and Y-axis plane circular measurement of ball bar
如图4所示,X、Y和C轴联动形成的球杆仪切线测量轨迹.可见,在球杆仪切线测量过程中,被测轴的旋转中心与球杆仪的球杆两端构成的三角形△OMN始终不变,且∠OMN=90°,圆环轨迹的小圆半径记为R.如图5所示,组合切线测量和平动轴圆轨迹测量的辨识原理.设切线测量和平动轴圆轨迹测量的杆长分别为L1、L2,则有

通过X和Y轴的平面圆轨迹测量(图3),得到径向误差Δlxy,其在切线测量(图5)时杆长方向的分量记为Exy,


图4 切线测量运动过程示意图Fig.4 Schematic diagram of tangential measurement process

图5 旋转轴转角定位误差辨识原理Fig.5 Identified principle of angular position errors of rotational axis
式中:θc为测量时C轴的转角位置.
旋转轴C的转角定位误差对切线测量杆长的影响Ec,由于转角定位误差角度εαc(θc)较小,可采用弧长公式近似计算:
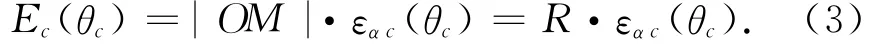
设切线测量的误差记为Δlxyc,则有

因此,旋转轴的转角定位误差可表达为
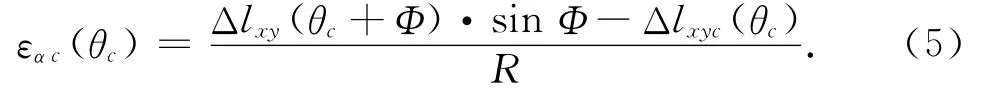
把式(1)代入式(5)便可计算得机床的转角定位误差.可见,对比传统的误差模型解耦求解过程[3], CPMM辨识旋转轴的转角误差具有简单、直观的优点.需要指出的是,本文所提测量方法以旋转工作台的C轴测量为例讲述其原理,但该方法可推广到其他类型的四轴及五轴机床.
3 模型仿真及结果分析
为了验证CPMM的可行性,首先采用模型仿真实验验证.以双转台五轴机床为研究对象(如图6所示).机床的成形运动由2个开环运动链构成:1)床身-Y方向运动轴-Z方向运动轴-主轴-刀具;2)床身-X方向运动轴-A摆动轴-C回转工作台-工件.
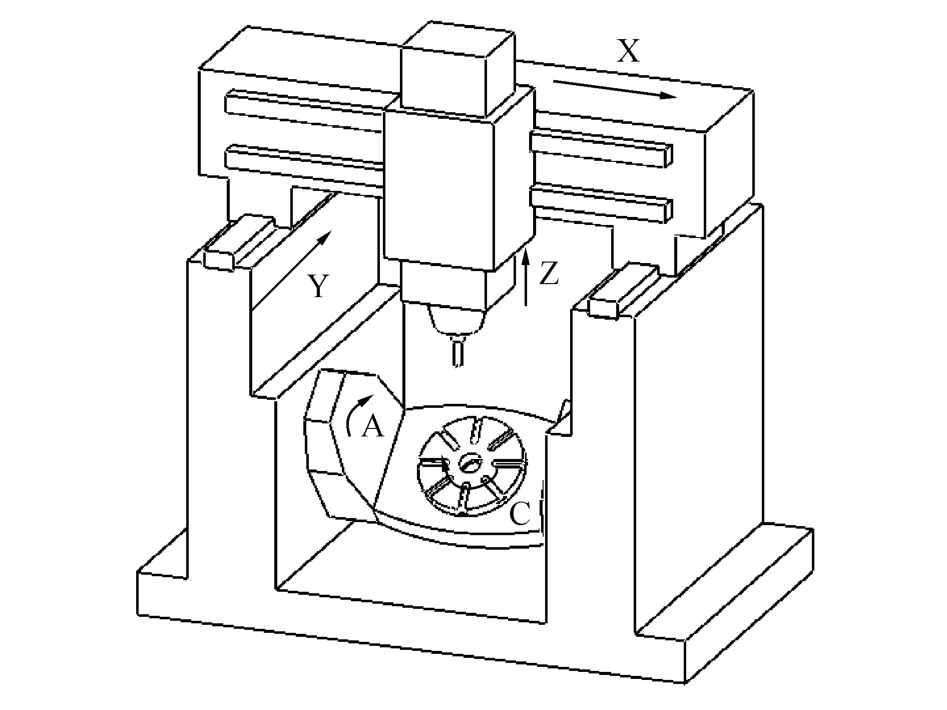
图6 双转台五轴数控机床结构示意图Fig.6 Schematic structural diagram of five-axis machine tool with a titling rotary table
根据机床空间运动学方程,球杆仪测量杆长矢量Γ可表示为
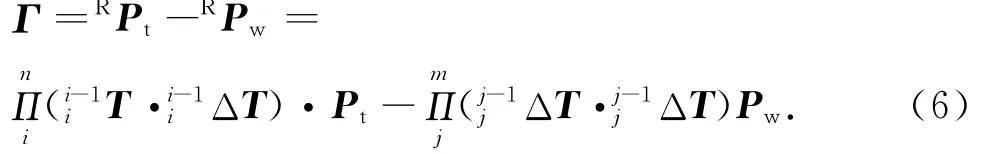
式中:Pt表示球杆仪安装在主轴的端点在刀具坐标系的齐次坐标,Pw表示球杆仪安装在工作台上的端点在工件坐标系的齐次坐标,RPt和RPw分别表示Pt和Pw在机床坐标系的齐次表达式T和ΔT表示运动部件i向其相邻低序体的理想传递矩阵和误差传递矩阵.传递矩阵齐次表达式可参见文献[13].
借助计算机对切线测量和2个平动轴圆轨迹测量进行仿真.机床各运动轴的运动误差参数由计算机随机生成,
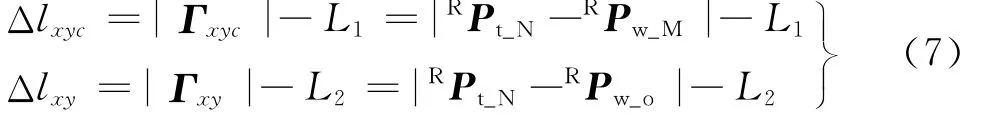
式中:RPt_N、RPw_M和RPw_o分别为切向测量时(图3)点N、M和O在机床坐标系的齐次坐标.
3.1 验证转角误差的敏感方向
C轴运动会产生6项运动误差,验证其他5项误差对切线测量的影响程度.为了更清淅地表明,假设X轴和Y轴为理想运动,即消除了平动轴圆轨迹运动产生误差的影响.给定C轴的各项误差参数,仿真切线测量并根据上述辨识方法计算转角定位误差εαc.如图7所示,给定转角定位误差和辨识计算得到的转角定位误差值.其中最大绝对误差是0.001 0°,最大相对误差是6.30%,计算值与给定值基本一致.表明了切线方向为转角定位误差的敏感方向.

图7 验证转角定位误差敏感方向的仿真结果Fig.7 Simulation results of sensitive direction of angular position errors
3.2 验证CPMM的可行性
设定机床各运动轴的误差参数,仿真切线测量和圆轨迹测量的实际轨迹,并根据上述辨识方法计算转角定位误差εαc.如图8所示,验证CPMM的仿真结果.可见,辩识结果与给定值基本上一致,但存在一些细微误差,最大绝对误差0.004 1°,最大相对误差20.13%.主要原因是:2个平动轴圆轨迹运动产生的位置误差矢量在测量平面上的分量,与理论径向存在一定的小角度偏差.仿真结果表明,这对辩识结果的影响并不大,故采用CPMM辨识旋转轴转角误差是可行的.

图8 验证CPMM的仿真结果Fig.8 Simulation results of CPMM
4 实验及结果分析
采用对照实验验证CPMM的可靠性.分别采用CPMM和激光测量方法[11]对数控机床的回转工作台进行测量.如图9所示,采用CPMM的五轴加工中心回转工作台转角定位误差测量实验.
如图10所示,球杆仪切线测量和平动轴圆轨迹测量结果.根据上述辨识方法,计算出转角定位误差εαc.同时,采用激光测量方法对回转台转角定位误差进行测量.如图11所示,球杆仪CPMM和激光测量方法的辨识结果.两者对同一运动误差的测量结果差异δ≤0.007 8°,可见,采用CPMM辨识的转角定位误差与激光测量方法的测量结果吻合较好.

图9 数控机床回转工作台转角定位误差测量实验Fig.9 Measurement experiment of angular position errors of CNC machine tool rotational table
5 结 论
本文提出组合路径测量方法(CPMM)对数控机床旋转轴转角定位误差进行测量.根据误差敏感方向,组合球杆仪切线测量和平动轴圆轨迹测量方法,对机床旋转轴转角定位误差进行辨识,可以避免繁琐的误差解耦过程,从而大大简化了辨识过程.该方法具有以下特点:
(1)机床测量操作简单,只需测量典型的球杆仪切线测量和平动轴圆轨迹测量,无需设置特殊测量路径;
(2)辨识过程不需要误差模型.与传统的球杆仪测量的误差模型辨识过程,该方法原理直观、简单易懂;
(3)与激光测量的安装相比,该测量方法安装简单,容易操作.
仿真实验表明切线方向是转角误差的敏感方向,同时验证了CPMM的可行性;与激光测量对照实验验证CPMM的可靠性.实验结果表明,该方法的辨识结果与激光测量结果差异,两者的结果吻合较好.因此,CPMM可用于旋转轴定位精度的评估以及为误差补偿提供依据.

图10 CPMM的测量结果Fig.10 Measurement results of CPMM

图11 CPMM和激光测量方法的辨识结果Fig.11 Identified results of CPMM and laser measurement
(References):
[1]SCHWENKE H,KNAPP W,HAITJEMA H,et al.Geometric error measurement and compensation of machines—an update[J].CIRP Annals-Manufacturing Technology,2008,57(2):660-675.
[2]LEI W,HSU Y.Error measurement of five-axis CNC machines with 3D probe-ball[J].Journal of Materials Processing Technology,2003,139(1):127-133.
[3]TSUTSUMI M,SAITO A.Identification and compensation of systematic deviations particular to 5-axis machining centers[J].International Journal of Machine Tools and Manufacture,2003,43(8):771-780.
[4]TSUTSUMI M,SAITO A.Identification of angular and positional deviations inherent to 5-axis machining centers with a tilting-rotary table by simultaneous four-axis control movements[J].International Journal of Machine Tools and Manufacture,2004,44(12):1333-1342.
[5]ZARGARBASHI S,MAYER J.Assessment of machine tool trunnion axis motion error,using magnetic double ball bar[J].International Journal of Machine Tools and Manufacture,2006,46(14):1823-1834.
[6]ZARGARBASHI S,MAYER J.Single setup estimation of a five-axis machine tool eight link errors by programmed end point constraint and on the fly measurement with Capball sensor[J].International Journal of Machine Tools and Manufacture,2009,49(10):759-766.
[7]ZHU S,DING G,QIN S,et al.Integrated geometric error modeling,identification and compensation of CNC machine tools[J].International Journal of Machine Tools and Manufacture,2012,52(1):24-29.
[8]张大卫,商鹏,田延岭,等.五轴数控机床转动轴误差元素的球杆仪检测方法[J].中国机械工程,2008,19(22):2737-2741.
ZHANG Da-wei,SHANG Peng,TIAN Yan-ling,et al.A DBB-based alignment error measurement method for rotary axis of 5-axis CNC machine tool[J].China Mechanical Engineering,2008,19(22):2737-2741.
[9]LEE K I,LEE D M,YANG S H.Parametric modeling and estimation of geometric errors for a rotary axis using double ball-bar[J].The International Journal of Advanced Manufacturing Technology,2012,62(5/8):741-750.
[10]李郝林,吴晓健.数控机床回转工作台转角误差测量方法:中国,201010256629.4[P].2010-12-15.
Li Hao-lin,Wu Xiao-jian.An angular errors measurement method for the rotational table of CNC machine tools:China,201010256629.4[P].2010-12-15.
[11]梁军,舒阳,黄宁秋,等.激光角度干涉仪测量数控转台位置精度的装置:中国,201010028151[P]:X, 2010-08-11.
Liang Jun,Shu Yang,Huang Ning-qiu,et al.An angular laser interferometer equipment to measure position errors of rotational table for CNC machine tools:China,201010028151,[P].X.2010-08-11.
[12]商鹏,阮宏慧,张大卫.基于球杆仪的三轴数控机床热误差检测方法[J].天津大学学报,2006,39(11):1336-1340.
SHANG Peng,RUAN Hong-hui,ZHANG Da-wei.Double-bal1-bar based thermal errors measurement method for 3-axis CNC machine tool[J].Journal of Tianjin University,2006,39(11):1336-1340.
[13]LIN Y,SHEN Y.Modelling of five-axis machine tool metrology models using the matrix summation approach[J].The International Journal of Advanced Manufacturing Technology,2003,21(4):243-248.
New method to measure angular position errors of rotational axis of CNC machine tool
HE Zhen-ya1,2,FU Jian-zhong1,XU Yue-tong1
(1.School of Mechanical Engineering,Zhejiang University,Hangzhou 310027,China;2.School of Mechanical and Automotive Engineering,South China University of Technology,Guangzhou 510640,China)
In order to carry out the error compensation of multi-axis machine tools,this paper presents a novel measurement method,a combined paths measurement method(CPMM)based on ball bar,to identify the angular position errors of a rotational axis of a machine tool.According to the error sensitive direction,angular position errors could be directly identified by combining the tangential direction measurement and circular path measurement of translational axes without a mathematical error model of a machine tool and the complicated error decouple process.The simulation and contrast experiments were conducted to verify the feasibility and reliability of the method.The results show that identified value by CPMM is consistent with that by laser measurement method,the maximum difference is 0.007 8°.The operation process of CPMM is simple and its corresponding identification algorithms are easier to understand.The established measurement method can be used for the precision evaluation of a rotational axis,and provide the basis for the error compensation to improve machining precision of machine tools.
rotational axis;angular position error;combined paths;ball bar;CNC machine tool
10.3785/j.issn.1008-973X.2015.05.004
TH 161
A
1008-973X(2015)05-0835-06
2014-04-23. 浙江大学学报(工学版)网址:www.journals.zju.edu.cn/eng
国家自然科学基金资助项目(51175461);高等学校博士学科点专项科研基金资助项目(20120101110055).
何振亚(1985-),女,博士,从事数控技术及相关方向的研究.E-mail:hezhenya@163.com
傅建中,男,教授,博导.E-mail:fjz@zju.edu.cn
下期论文摘要预登
