考虑测控约束的非特殊点双冲量变轨规划算法研究

吕纪远，张海联，叶东明，李九人

（载人航天总体研究论证中心，北京 100094）

考虑测控约束的非特殊点双冲量变轨规划算法研究

吕纪远，张海联，叶东明，李九人

（载人航天总体研究论证中心，北京 100094）

非特殊点双冲量变轨问题中，使用近地点远地点双冲量变轨可以得到最优的速度增量，但没有考虑测控覆盖范围的约束。针对这个问题，对一般椭圆轨道的双脉冲变轨问题进行了介绍，在此基础上，将测控约束与非特殊点双脉冲变轨问题进行综合考虑，借助轨道外推、测控覆盖分析得到一套变轨规划算法，能够在考虑测控覆盖的约束下得到非特殊点双冲量变轨的最优解。仿真结果表明，规划算法优化出的速度增量与特殊点变轨相比增加很少，且发动机工作期间满足测控约束。

非特殊点变轨；双脉冲；测控约束

1 引言

轨道机动和轨道控制方法很多，尤其对于轨道面内的升降轨机动，研究颇为成熟。已知两个共面圆轨道之间的过渡，霍曼变轨是最省燃料的方式；而对于共面同轴同向椭圆轨道之间的过渡，文献［1］中亦有证明：在小椭圆近地点和大椭圆远地点施加脉冲最省燃料。但是，在具体与工程实际结合方面，常规的轨道控制理论仍有诸多需要补充的地方。对于有测控弧段约束，无法在特殊点变轨的共面椭圆，如何在测控弧段内实现其最省燃料的机动方式，是许多航天器轨道控制必须解决的关键问题。

本文针对共面椭圆轨道之间的非特殊点变轨进行研究，轨道机动位置不在近地点或远地点。Lawden［2］和Bender［3］早在1962年就对这种一般性轨道控制问题开展了研究，提出了180°对称周向控制的最佳模式，但是我国的实际测控条件并不一定能满足相位差180°的要求，这就对实际工程应用提出了较为苛刻的约束。本文对一般性轨道控制算法进行推导，然后借助优化算法，解决了机动控制中从任意范围的真近点角施加脉冲，将小椭圆轨道变为大圆轨道的最优控制问题。

2 一般椭圆双脉冲轨道控制数学模型

首先介绍一般椭圆的双脉冲变轨算法［4］。

令（1）、（2）、（T）分别表示初始轨道、目标轨道和转移轨道，下标1、2、T表示轨道（1）、（2）、（T）的参数，第二下标表示在第一下标轨道上该参数的条件（见图1）。例如，f1T表示在初始轨道上向转移轨道过渡的脉冲作用点的真近点角。由于转移轨道的拱线与初始轨道的拱线并不一定重合，因此一般情况下f1T≠fT1。

图1 双脉冲拱线变轨示意图Fig.1 Two-impulses orbit transfer method

令转移轨道相对于初始轨道的转动控制值为ΔωT，目标轨道相对于初始轨道的转动控制值为Δω，则脉冲作用点真近点角的关系如式（1）：

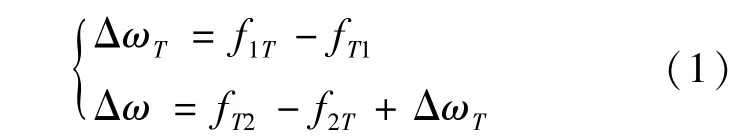
如图1所示，在第一脉冲作用点，有式（2）：

在第二脉冲作用点，有式（3）：

上述各式中vr、vt表示径向、切向速度。两次脉冲总的速度增量Δv可以由（2）和（3）联立得式（4）：

确定双脉冲拱线变轨最省燃料的过渡方式，就是在一定的约束条件下求Δv的极小值。

3 考虑约束的轨道机动规划算法

3.1 约束条件

我国地面测控覆盖范围有限，对变轨时刻存在较大约束。为确保机动过程可控，一般情况下，要求轨控发动机工作时航天器要在测控弧段内。基于节省燃料的考虑，变轨点通常选在近地点和远地点附近，考虑测控约束条件下一般的做法是，对近地点和远地点测控覆盖情况进行筛选，在满足测控条件的圈次对轨道机动的速度增量进行迭代优化。

航天器初始轨道与初始目标轨道是另一组约束条件。本文设定目标椭圆与原轨道共面，且指定其偏心率e2和长半轴a2作为目标约束。

3.2 规划算法

规划算法分为三步，具体为：

1）轨道外推和筛选第一次变轨点

根据初始轨道要素和高精度轨道动力学模型对轨道进行外推，同时按照测站位置数据筛选每圈会经过哪些测站，以距离测站最近的点作为变轨点，进而得到一系列可用的脉冲变轨点集合，用真近点角表示为｛f1T｝。

2）用优化算法确定最佳转移的Δv1和Δv2

首先分析两次变轨所需的速度增量与哪些变量相关：

根据椭圆运动方程，可知在第一次变轨点，有式（5）：r1T

是第一次脉冲作用点的地心距，令rT1为转移轨道上第一次脉冲作用点的地心距，则r1T=rT1，并且有式（6）：

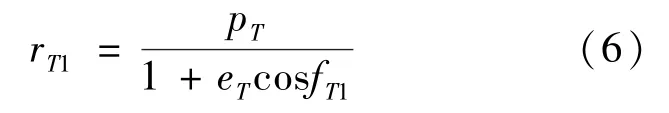
式（6）中有三个未知数，fT1、eT和pT，可将fT1作为待优化的变量，列方程组求解转移轨道的偏心率eT和半通径pT。

方程组的第一个方程根据r1T=rT1给出，第二个方程可根据第二次脉冲作用点的r2T=rT2给出，即式（7）：

式（7）中，fT2同（6）中的fT1一样作为待优化变量。由于目标轨道只约束轨道长半轴a2和偏心率e2，没有约束f2T，因此f2T也需要作为待优化变量。式（5）、（6）和（7）构成方程组如式（8）：

方程组（8）中，已知量为初始轨道的e1、p1、f1T和目标轨道的e2、p2，待优化变量为三个真近点角fT1、fT2和f2T，可以用这些量表示et和pt如式（9）：

进而根据（2）、（3）和（4）求得速度增量Δv。

在上述理论的基础上，选择一套优化算法对三个脉冲变轨点fT1、fT2和f2T进行优化即可，即在给定的初始轨道和脉冲变轨点集｛f1T｝，以及目标轨道长半轴a2和偏心率e2的条件下，使用方程组（9）和（2）、（3）、（4）求得最小的双脉冲转移速度增量Δv。

此规划算法适用于目标轨道为任意椭圆的情形，当目标轨道的偏心率e2=0，待优化变量减少为fT1和fT2两个时，计算可简化。

3）得出整个变轨规划的结果

根据第二步的优化结果，将Δv1在对应的位置上进行施加，考察在给定的发动机推力下，施加速度增量Δv1会不会导致开关机点在测控覆盖范围外，从而筛选出第一次变轨的施加圈次；然后考察在给定的发动机推力下，施加Δv2时的第二变轨点经过哪些测站，并确保开关机点在测站覆盖范围内，从而筛选出第二变轨点的变轨圈次，得出整个变轨规划的结果。

对于第一步和第三步，通过测控覆盖分析完成；对于第二步优化，可考虑使用0～360°遍历三个待优化角度的方法获得最小速度增量Δv，以得到全局最优解。

4 仿真

4.1 参数设置

以常见的近地小偏心率椭圆轨道为例，验证双冲量变轨算法有效性，此变轨需求常见于入轨后轨道圆化或航天器升轨控制。设航天器的初始轨道历元为2014年7月30日00：00：00，初始轨道参数见表1，变轨的目标轨道为400 km圆轨道。

表1 航天器初始轨道要素Table 1 The initial six orbit elements

航天器质量设置为5000 kg，推力器推力为1000 N，大气阻力面质比为0.004，考虑地球J2摄动，所使用的地面测站包括目前我国在全球的所有可用测站。

规划和仿真的步长为1 s，考察航天器过测站的情况，以5°仰角为测站观察范围。

4.2 规划结果

按照3.2节规划算法的第一步，得到的可用真近点角集合｛f1T｝整理如表2（仅截取第四圈过测站的结果）。

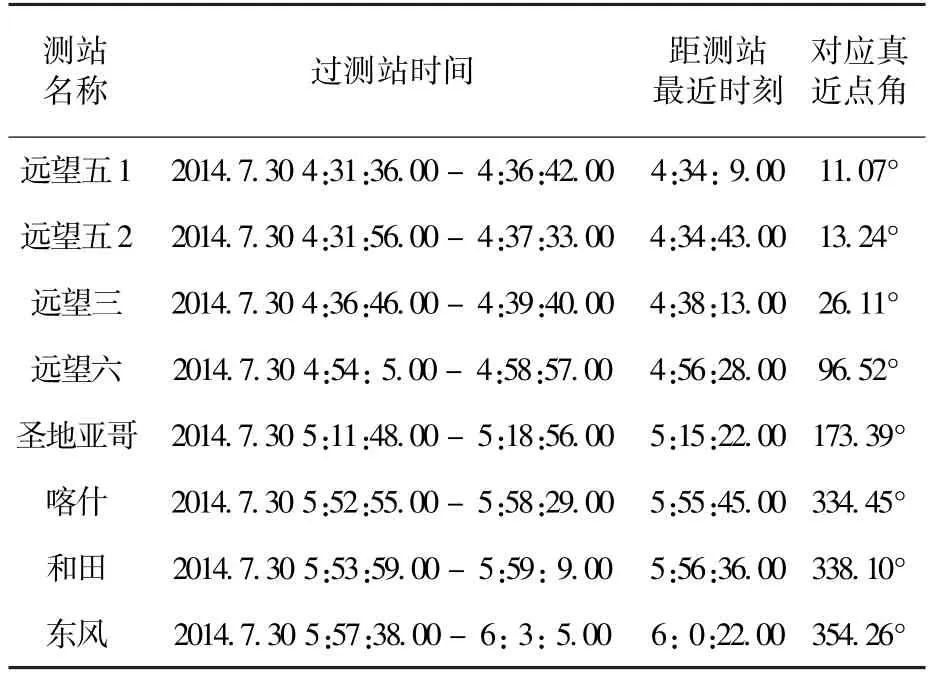
表2 第四圈过测站情况统计Table 2 The statistics of passing the measurement stations in circle 4

此时可以根据其它工程具体约束选择施加第一次变轨脉冲的真近点角，本文选择在远望五1的测控覆盖区内实施第一次脉冲，即真近点角为11.07°时作为标称脉冲施加点。

然后根据步骤二优化得到相应的速度增量和转移轨道参数，结论如下：

此方法所需总的速度增量为56.56 m/s，而理论上最优的近地点远地点变轨方案所需的总的速度增量为56.32 m/s，可见差别很小。

然后按照3.2节第三步，以第四圈的f1T点为基准，考察第二次脉冲时间点过测站情况（截取第五圈情况统计，见表3）。

其中在测站圣地亚哥附近，可以实现施加航天器轨控发动机工作时的测控覆盖，从而得到整套变轨流程：以第四圈f1T=11.07°为基准施加第一次速度增量，Δv1=8.69 m/s；以第五圈fT2=180.00°为基准施加第二次速度增量，Δv2= 47.89 m/s。总的速度增量仅比理论最优方案增加0.34 m/s。

表3 第五圈过测站情况统计Table 3 The statistics of passing the measurement stations in circle 5

本算例仅针对一次一般性的变轨需求进行了算法验证，事实上，此算法可对任何涉及测控覆盖约束的共面变轨需求进行求解，从结论中可以看出，相对于最优的霍曼转移，变轨速度增量增加很小。

5 结论

本文所设计的变轨规划策略，从算法角度就考虑了非特殊点变轨问题，并将测控范围作为基本约束，与现有做法相比，优点在于不需要多次迭代计算，可直接求得在考虑实际测控覆盖范围约束下的共面轨道机动策略。此外，由于求解过程中引入优化，最终所需速度增量与特殊点变轨相比也增加很少。本文从工程实际角度引入约束并进行求解，所得算法可为实际应用提供参考。

（

）

［1］ 刘暾，赵钧.航天器轨道动力学［M］.哈尔滨工业大学出版社.哈尔滨.2011：41-45.

Liu Dun，Zhao Jun.The Spacecraft Orbital Dynamics［M］. Harbin：Harbin Institute of Technology Press，2011：41-45. （in Chinese）

［2］ Lawden D F.Impulsive Tranfer between Elliplical Orbits in Optimization Techniques［M］.Leitmann G..Academay Press，1962：107-122

［3］ Bender D F.Optimum coplanar two-impulse transfer between elliptic orbits［J］.Aerospace Enginering 1962（10）：56-63.

［4］ 章仁为.卫星轨道姿态动力学与控制［M］.北京航空航天大学出版社.北京，2006：77-79.

Zhang Renwei.Satellite Orbit Attitude Dynamics And Control ［M］.Beijing：Beihang University Press，2006：77-79.（in Chinese）

Research on Non-special Points Two-impulse Orbit Transfer Planning with Tracking，Telemetry and Control Constraints

LV Jiyuan，ZHAGN Hailian，YE Dongming，LI Jiuren
（Manned Space System Reasearch Center，Beijing 100094，China）

The problem of non-special points two-impulse orbit transfer was studied.In general，the application of special points orbit transfer method can get optimal result.However，this method doesn't take into account the tracking，telemetry and control（TT&C）constraints.In this paper，the two-impulse transfer of ellipse orbit was introduced at first.Then，considering the TT&C constraints，the method of orbit extrapolation and TT&C coverage analysis were used to get a new algorithm.Simulation result shows that the velocity increment obtained by the new algorithm is only a little more than that of the optimal result，and can meet the TT&C constraints during the engine firing.

non-special points orbit transfer；two-impulse；tracking，telemetry and control（TT&C）constraints

V556

A

1674-5825（2015）06-0560-04

2014-07-30；

2015-08-24

吕纪远（1984-），男，博士，助理研究员，研究方向为载人航天任务分析与仿真。E-mail：kokyo52@163.com