漂浮基柔性臂空间机器人输出力矩受限的自适应PID输出反馈

张丽娇，陈 力

（1.福州大学机械工程及自动化学院，福州 350108；2.福建省高端装备制造协同创新中心，福州 350116）

漂浮基柔性臂空间机器人输出力矩受限的自适应PID输出反馈

张丽娇1，2，陈 力1，2

（1.福州大学机械工程及自动化学院，福州 350108；2.福建省高端装备制造协同创新中心，福州 350116）

针对输出力矩受限的漂浮基柔性臂空间机器人的控制问题，结合系统动量守恒关系和拉格朗日方法建立了系统动力学模型；利用奇异摄动法，慢变子系统设计了输出力矩受限情况下仅有位置传感、建模不确定性及干扰的空间机械臂系统协调运动的自适应PID输出反馈控制算法，快变子系统设计了线性二次最优控制方法主动抑制。该算法采用高精度滤波器估计机器人关节速度，使得整个系统的闭环控制仅需位置输出反馈；在控制率中引入饱和函数，保证输出力矩在给定限制范围内，同时采用自适应PID控制器补偿建模不确定性和干扰。基于Lyapunov稳定性理论证明了该算法可确保控制系统是渐近稳定的，针对平面两关节漂浮基柔性臂空间机器人的仿真结果表明了所提出的控制方案良好的跟踪性和快速收敛性。

柔性臂空间机器人；奇异摄动；自适应PID控制；输出力矩受限

1 引言

空间机器人是用于空间探测活动的特种机器人。目前，有关空间机器人系统的结构设计和控制方法研究已成为空间科学研究和机器人技术研究的重点［1-6］。在空间实际应用当中，空间机器人的机械臂往往质量较轻、惯量较小，这使得机械臂在高速运动过程中容易发生变形，因此空间机器人的机械臂常使用柔性杆来进行操作，对柔性空间机械臂的研究也成为自20世纪80年代后空间机器人的研究重点。

考虑到柔性臂空间机器人系统动力学方程的阶数多于地面刚性机械臂，且由于柔性杆的振动频率一般比系统刚性振动频率高，使用奇异摄动法将可以对柔性臂空间机器人系统的包含振动模态的动力学方程进行降阶处理，将其分解为两种时间尺度的奇异摄动模型。文献［7］使用奇异摄动法考虑了一类机械系统的高阶滑模控制问题并进行了实验研究。本文将奇异摄动方法应用到柔性臂空间机器人控制器设计中，讨论了载体位置不受控、姿态受控情况下，漂浮基柔性臂空间机器人输出力矩受限的自适应PID输出反馈问题。首先，利用拉格朗日假设模态法并结合系统线动量守恒关系，建立了柔性臂空间机器人系统的动力学方程。以此为基础，使用两种时间尺度的假设，将系统分解为轨迹跟踪控制器和振动控制器可分开设计的奇异摄动系统。

针对实际机器人轨迹跟踪控制中存在的问题，例如仅位置传感、驱动器饱和、存在建模不确定性及干扰，为满足高精度运动控制的要求，提出了众多先进控制和智能控制算法，如，计算力矩法、自适应控制、变结构控制、迭代学习控制、鲁棒控制、模糊控制、神经网络控制等［8-9］。但这些算法因假设条件较多，计算复杂，针对性强等限制其实际的应用。迄今为止，实际工业应用中的大多数商品化的机器人控制器的控制策略是基于独立关节PID伺服算法，该算法结构简单，易于设计，在一定程度上满足控制系统的要求［10］。

对于系统模型存在不确定性和干扰的研究较多，典型的是采用鲁棒控制和自适应控制算法［11］；对于只基于关节位置信号的输出反馈控制，较为典型的是采用观测器［12］和滤波器［13］；在输出力矩饱和受限的情况下，典型的是采用基于tanh（x），sat（x）等饱和函数的饱和PD+控制器［14］。

针对上述问题，本文对于快变子系统，使用全局最优控制来对柔性杆件的振动进行主动抑制。对于慢变子系统，设计了输出力矩受限情况下仅有位置传感、建模不确定性及干扰的空间机械臂系统协调运动的自适应PID输出反馈控制算法。

2 柔性臂空间机器人系统动力学分析

考虑作平面运动的自由漂浮基柔性臂空间机器人的几何模型如图1所示。其中，B0为系统的刚性载体基座，B1为系统的刚性连杆，B2为系统的柔性连杆（可视为Euler-Bernoulli悬臂梁且仅产生横向振动），Bi-1和Bi（i=1，2）间均使用刚性旋转铰进行联接。建立各分体Bi（i=0，1，2）的主轴联体坐标系（Oi-xiyi），O1、O2分别为相应两个转动铰的中心；x0通过O0与O1的连线，x1和x2分别是B1和B2的对称轴，ei为沿xi（i=0，1，2）轴方向的基矢量；C为系统总质心。mi、ji分别为Bi（i=0，1，2）的质量与中心转动惯量，B2单位长度的均匀质量密度为ρ，均匀弯曲刚度为EI，M为系统总质量；并定义q0为航天器载体姿态角，q1和q2为关节O1、O2的相对转角。

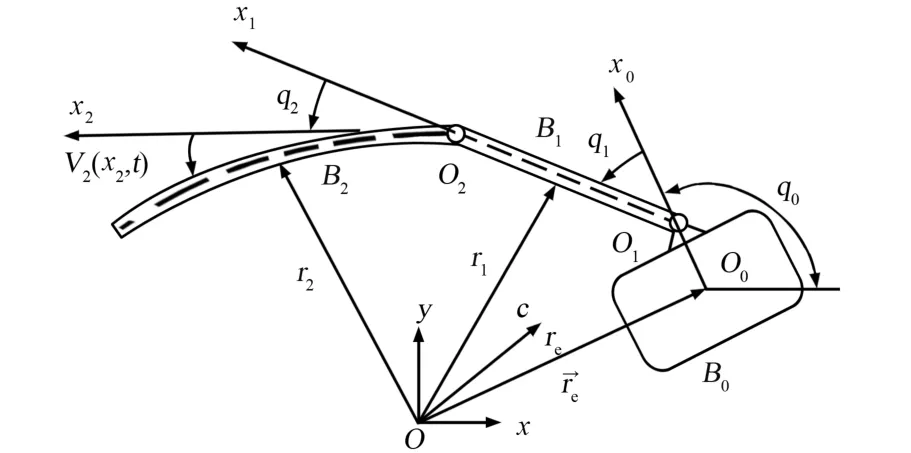
图1 漂浮基柔性臂空间机器人系统Fig.1 Free-floating flexible manipulator space robot system

由弹性理论可知，基于假设模态变形描述法，横向弹性变形v（x2，t）可描述为式（1）：

其中，ϕi（x2）和δi（t）分别为柔性杆的第i阶模态函数及其坐标，n为截断阶数。考虑到低阶模态对杆件的弹性振动起主导效应，本文取前二个低阶模态进行研究，即式（2）：

利用拉格朗日法和动量守恒关系，可导出式（3）所示载体位置不受控和姿态受控的柔性臂空间机器人动力学方程：

其中，M（q，δ）∈R5×5为正定、对称惯性阵；H（q，δ，q·，δ·）∈R5×5为从包含离心力、科氏力列向量中分离出来的矩阵；q=［q0q1q2］T，δ= ［δ1δ2］T分别为系统广义坐标列向量的刚性变量、柔性变量；Kδ=diag［kδ1kδ2］为系统的抗弯刚度阵；τ=［τ0τ1τ2］T为系统的控制力矩列向量。

3 系统动力学奇异摄动分解

据式根据式（3），姿态受控柔性臂空间机器人的动力学模型可展开为式（4）：

若约定式（5）：

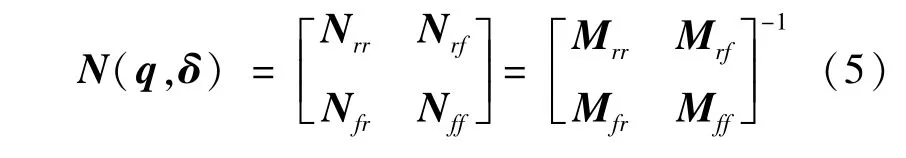
则式（4）可转化为式（6）：

若定义μ=1/min［kδ1，kδ2］为奇异摄动因子σ=δ/μ、Ks=μKδ，则式（6）可变换为式（7）：

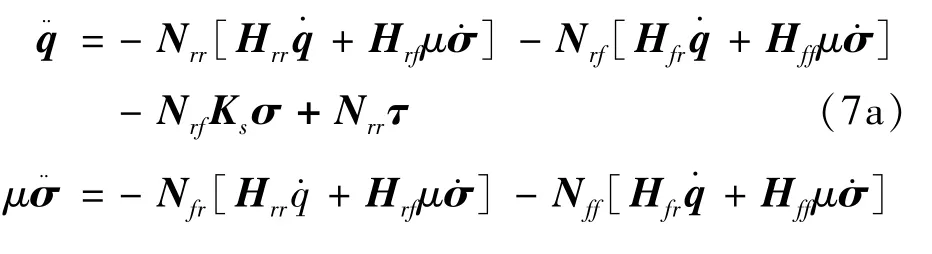
令μ=0并将其代入式（7），得式（8）所示慢变子系统：

其中，带“—”的变量表示机器人的慢变分量，τs表示慢变控制律。则慢变子系统（8）满足如下性质［15］：

令μ=0，并结合快、慢时标的相互独立性及式（7），可得到式（10）～（11）所示快变子系统的动力学方程：

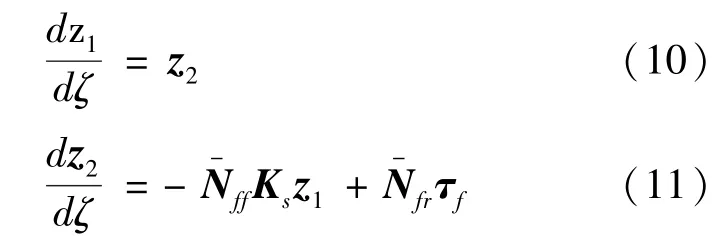
于是，可得快变子系统如式（12）：

最终，式（8）和式（12）共同构成了系统的奇异摄动模型且τ=τs+τf。

4 控制方法设计

4.1 慢变子系统的自适应PID输出反馈控制法设计

据第3节可知，柔性臂空间机器人系统式（4）可被降阶分解为快、慢变两个子系统式（8）和式（12）。由于这两个子系统在时标上具有独立性，故我们可分别对每个子系统进行相应控制器的设计，并最终组成系统的总控制器。

基于式（8），将设计一种基座姿态与关节协调操作运动的模糊终端滑模慢变子控制器。若令q=［q0q1q2］T为系统的实际输出，qd= ［q0dq1dq2d］T为其理想输出，则系统追踪误差可描述为式（13）：

考虑只有位置信息可测，定义滤波误差函数为式（14）：

其中，Λ为一正定矩阵，Λ=ΛT＞0，则有（15）：

考虑参数的不确定性和外部扰动，式（8）可以表示为式（16）：

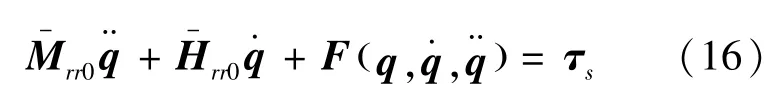
根据式（21）可以表示为式（17）：

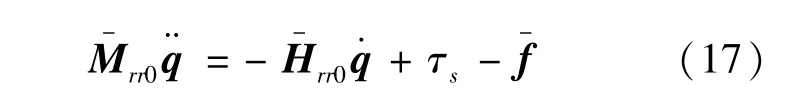
连续型PID控制设计如式（18）：

其中，Kp，Ki，Kd分别为比例、微分、积分增益。

式（18）可以写成如式（19）形式

PID控制器τpid（e|θk）可以一致逼近系统不确定项，因此，存在一最优参数向量θ*，使得近似误差有界。即式（20）：

其中，θ*满足式（21）：Ωθ、Ωe分别为θ、e的期望约束集。

这里仅需要知道存在最优参数向量θ*，用于收敛分析，而不必知道其确定值，它对控制器的设计不是必需的。令满足式（22）：

控制器设计如式（23）～（25）：

其中，v为滤波器的输出，kw＞0，Γ为一正定矩阵。K=diag［k1，…，kn］，β=diag［β1，…βn］，tanhv=［tanhv1，…，tanhvn］T，tanhv∈Rn，K，β∈Rn×n，k1，…，kn，β1，…，βn，α皆为正常数。

定义Lyapunov函数如式（26）：

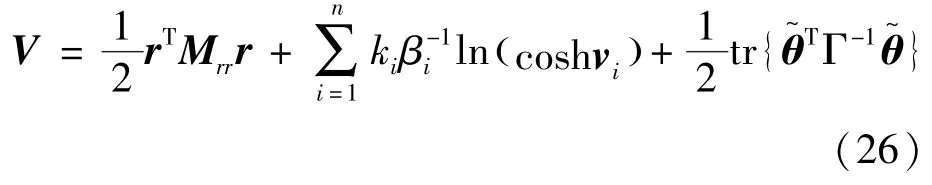
式（26）为一正定函数，沿闭环系统轨迹的微分如式（27）：

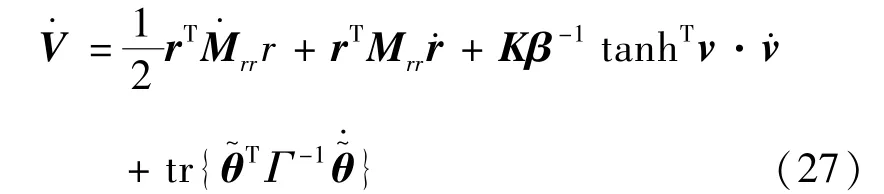
其中，

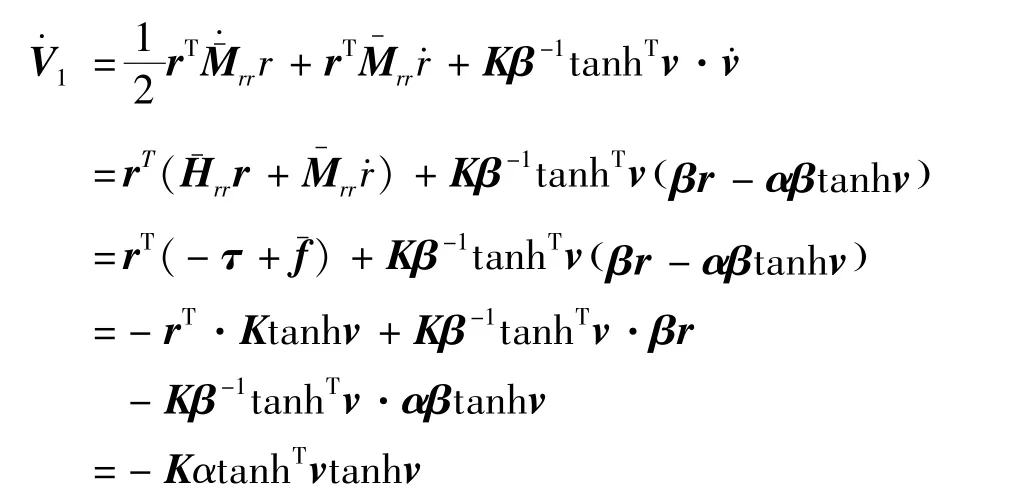
根据F范数的性质［16］，有式（28）：

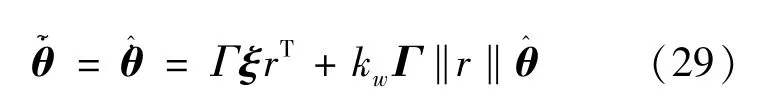
则

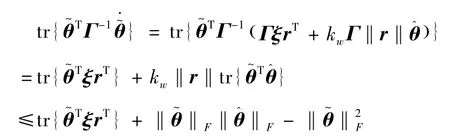
由式（27）、式（28）、式（29）得式（30）：

其中参数c1、V1分别满足式（31）、（32）：

由式（31）、式（32）可知，当选取较大的K和较小的kw，可以得到较大的收敛区域。

由式（14）、式（24）可知，滤波器的输出只和关节位置信号及e·有关，因此，不需要关节速度和加速度信号。

4.2 快变子系统—柔性臂振动主动抑制的基于状态观测器的最优控制方法设计

为抑制弹性振动，本节拟采用基于状态观测器的最优控制策略来对快变子系统式（12）进行控制。快变子系统经变换后呈线性系统，故采用简单的最优控制即可快速有效地抑制振动。因此定义系统性能指标函数如式（33）：

其中，Rf∈R3×3和Qf∈R4×4分别为正定、半正定常值阵。被积函数中第一项表示动态过程中对控制的约束或要求，是用来衡量控制功率大小的代价函数。被积函数中第二项Lz=zTQfz，是用以衡量误差z大小的代价函数，z越大，则支付的代价越大。最优控制的目标是使Jf→min，则其实质在于用不大的控制，来保持较小的误差，从而达到能量和误差综合最优的目的。

设Pf为式（34）所示Ricatti方程的唯一解［17］：

则快变最优控制律可定义为式（35）：

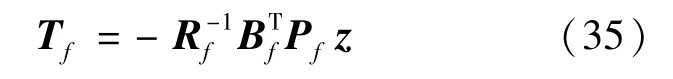
5 仿真算例

以图1所示作平面运动的两杆漂浮基柔性臂空间机器人系统为例。仿真过程中我们假定系统中各参数为：m0=40.0 kg，m1=2.0 kg，j0= 34.17 kg·m2，j1=1.5 kg·m2，l0=1.5 m，l1= 3.0 m，l2=3.0 m，ρ=1.0 kg/m，EI=200 N·m2。并假设柔性杆B2的杆长l2和单位长度的均匀质量密度ρ为系统未知参数，仿真过程中其真值取为l2=3.0 m，ρ=1.0 kg/m。

系统的柔性杆B2被视为Euler-Bernoulli悬臂梁，其模态试函数ϕi（x2）取为ϕi（x2）= Ai［cos（υix2）-cosh（υix2）］+［sin（υix2）-sinh（υix2）］，其中，Ai=-［sin（γi）+ sinh（γi）］/［cos（γi）+cosh（γi）］，（i=1，2），υi=γi/l2，γ1=1.8751，γ2=4.6941。

建模不确定与干扰力矩为：τd1=sint，τd2= cost。

仿真时间：t=25 s，控制参数为K= diag［10，6，4］，Γ=［1］，α=diag［4，3，2］，kw= 0.001，Λ=diag［2.5，2，1.5］，β=diag［5，2，1］。

PID初始值为：Kp=diag［50，50，10］，Kd= diag［100，100，5］。

图2 载体姿态运动轨迹Fig.2 The trajectory of the base's attitude

仿真结果如图2～图7所示。其中，图2为载体姿态的运动轨迹跟踪图；图3为机械臂关节绞的运动轨迹跟踪图；图4为机械臂关节绞的运动轨迹跟踪误差；图5为漂浮基柔性臂空间机器人系统完成轨迹跟踪所需的驱动力矩图；图6为柔性臂的模态坐标变化曲线图；图7为柔性臂末端变形曲线图。

图3 机械臂关节绞运动轨迹Fig.3 The trajectories of the manipulator's joints

图4 机械臂关节绞的运动轨迹跟踪误差Fig.4 The trajectory tracking errors of the manipulator's joints

图5 驱动力矩Fig.5 The driving torques

图6 柔性臂模态坐标的变化曲线Fig.6 Curves of the mode coordinates of the manipulator

图7 柔性臂末端变形曲线Fig.7 Curves of the flexible manipulator's deformation

由图2和图3可看出，在本文所提出的混合控制方法的控制下，漂浮基柔性臂空间机器人的载体姿态和机械臂的关节绞都能够精确且稳定地跟踪上他们的期望运动轨迹，完成控制任务；图4可看出，本文所提出的自适应PID输出反馈控制算法能够适应输出力矩受限的实际应用情况；图6和图7可看出，柔性臂的弹性变形得到了有效的补偿，且柔性臂所引起的系统弹性振动也得到了有效的抑制，系统的控制精度和稳定性得到了保证。

6 结论

本文对柔性空间机械臂系统进行动力学分析，结合系统总质心定义得到的系统动力学方程对一组选择的系统参数组合函数呈线性关系。使用奇异摄动理论和两个时间尺度的假设，将系统分解为快变和慢变两个子系统的奇异摄动模型。针对实际机器人轨迹跟踪控制中存在的问题，慢变子系统使用自适应PID饱和输出反馈控制，给出系统稳定性的条件；同时，快变子系统使用最优控制理论来对柔性杆的振动进行主动振动抑制。仿真结果表明，本文所提出控制算法能使系统机械臂关节快速地追踪上期望轨迹并在短时间内对产生的振动进行抑制。此外，由于不需控制整个系统载体的位置，还大大减少了喷气装置的燃料消耗，延长了空间机械臂的有效使用寿命。

（

）

［1］ Mansour T，Konno A，Uchiyama M.Modified PID control of a single-link flexible robot［J］.Advanced Robotics，2008，22 （4）：433-449.

［2］ Heidari F，Vakil M，Fotouhi R.On the accuracy of assumed mode modeling for flexible manipulators［C］//Proceedings of the ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.New York，NY，United States：ASME，2011. 953-962.

［3］ Celentano L，Coppola A.A computationally efficient method for modeling flexible robots based on the assumed modes method［J］.Applied Mathematics and Computation，2011，218 （8）：4483-4493.

［4］ 洪在地，贠超，陈力.柔性臂漂浮基空间机器人建模与轨迹跟踪控制［J］.机器人，2007，29（1）：92-96.

Hong Zaidi，Yun Chao，Chen Li.Modeling of trajectory tracking control of free-floating space robot with flexible manipulators［J］.Robot，2007，29（1）：92-96.（in Chinese）

［5］ 王从庆，吴鹏飞，周鑫.基于最小关节力矩优化的自由浮动空间刚柔耦合机械臂混沌动力学建模与控制［J］.物理学报，2012，61（23）：81-88.

Wang Congqing，Wu Pengfei，Zhou Xin.Control and modeling of chaotic dynamics for a free-floating rigid-flexible coupling space manipulator based on minimal joint torque's optimization［J］.ActaPhysisSinica，2012，61（23）：81-88.（in Chinese）

［6］ 梁捷，陈力.具有时延的漂浮基空间机器人基于泰勒级数预测、逼近的改进非线性反馈控制［J］.航空学报，2012，33（1）：163-169.

Liang Jie，Chen Li.Improved nonlinearfeedback control for free-floating space-based robot with time-delay based on predictive and approximation of taylorseries［J］.ActaAeronautica ET AstronauticaSinica，2012，33（1）：163-169.（in Chinese）

［7］ Cavallo A，Natale C.High-order sliding control ofmechanical systems：Theory and experiments［J］.Control Engineering Practice，2004，12（9）：1139-1149.

［8］ Feng B M，Ma G CH，Xie W N et al.Robust tracking control of space robot via neural network［J］.Systems and Control in Aerospace and Astronautics，2006，902-906.

［9］ Gorinevsky D，Kapitanovsky A，A Goldenberg.Radial basis function network architecture for nonholonomic motion planning and control of free-flying manipulators［J］.IEEE trans. on Robotics&Automation，1996，12（3）：491-496.

［10］ Lia W，Changa X G，Wahlb F M，etal.Tracking control of a manipulator under uncertainty by fuzzy PID controller［J］. Fuzzy Sets and System，2001，122（1）：125-137.

［11］ Abiko S，Hirzinger G.Adaptive control for a torque controlled free-floating space robot withkinematic and dynamic model uncertainty［C］//Proceedings of the 2009 IEEE/RSJ InternationalConference on Intelligent Robots and Systems.Piscataway，NJ，United States：IEEE，2009.2359-2364.

［12］ Koofigar H R.Adaptive tracking with external force disturbance rejection for uncertain robotic systems［J］.International Journal of Control Automation and Systems，2014，12（1）：169-176.

［13］ Masahio O，Chun Y S，Toshihiro K.State observer-based robust control scheme for electrically driven robot manipulators ［J］.IEEE Trans on Robotics，2004，20（4）：796—804.

［14］ Su Yuxin，Muller P C，Zheng Chunhong.A global asymptotic stable output feedback PID regulator for robot manipulators ［C］//Proceedings of IEEE International Conference On Robotics and Automation，Roma：IEEE Press，2007：4484-4489. ［15］ Peng L，Woo Peng-Yung.Neural-fuzzy control system for robotic manipulators［J］.Control Systems Magazine，2002，22 （1）：53-63.

［16］ 张文生.科技计算中的偏微分方程有限差分法［M］.北京：高等教育出版社，2006.

ZhangWensheng.Scientific computing in the finite difference methods for partial differential equations［M］.Beijing：Higher Education Press，2006.（in Chinese）

［17］ 戈新生，崔玮，赵秋玲.刚柔性耦合机械臂轨迹跟踪与振动抑制［J］.工程力学，2005，22（6）：188-191.

GE Xinsheng，CUI Wei，ZHAO Qiuling.Trajectorytracking control and vibration suppression of rigidflexible manipulators ［J］.Engineering Mechanics，2005，22（6）：188-191.（in Chinese）

［18］ Moreno-Valenzuela J，Santibanez V，Campa R.A class of OFT controllers for torque—saturated robot manipulators：Lyapunov stability and experimental evaluation［J］.Journal of Intelligent and Robotic Systems，2008，51（1）：65-88.

［19］ Yu Wen-shyong.Adaptive fuzzy PID control for nonlinear systems with H∞tracking performance［C］//Proceedings of IEEE International Conference on Fuzzy Systems，Vancouver：IEEE Press，2006：1010-1015.

Adaptive PID Output-Feedback Control of Free-floating Flexible Manipulators Space Robot with Bounded Torque Output

ZHANG Lijiao1，2，CHEN Li1，2
（1.School of Mechanical Engineering and Automation，Fuzhou University，Fuzhou 350108，China；2.Collaborative Innovation Center of High End Equipment Manufacturing，Fuzhou 350116，China）

The control problem of the free-floating flexible manipulators space robot with bounded torque outputs was discussed.With the momentum conservation relations，system dynamics model was set up by the Lagrange method.Based on the singular perturbation method，an adaptive PID output-feedback control algorithm was designedin the slow subsystemwith only position measurements，modeling uncertainties and disturbances under space robot manipulators'coordinated motion with limited output torque，and a linear-quadratic optimal control was designed in the fast subsystem. High precision filter was used in the algorithm to estimate the joint velocity of the manipulators，which made the whole closed-loop control with only position feedback measurements.A saturation function was introduced in the control law，which guaranteed the output torque within any specified range.While an adaptive PID controller was used to compensate the modeling uncertainties and interferences.Based on Lyapunov stability theory，this algorithm is proved to be able to ensure that the control system is asymptotically stable.The simulation results based on a planar two-joint freefloating flexible manipulators space robotshow that the proposed control scheme is designed with good trajectory tracking and fast convergence.

flexible manipulators space robot；singular perturbation method；adaptive PID control；bounded output torque

TP242.3；V447

A

1674-5825（2015）06-0568-07

2014-09-10；

2015-09-08

国家自然科学基金资助项目（11372073）

张丽娇（1989-），女，博士研究生，研究方向为空间机器人控制。E-mail：lijiaoz@126.com