在自主编题中培养学生的数学能力

马丽

【内容摘要】自主编题是培养学生解读数学概念、培养数学思维和实践能力的有效途径，是中考的常考题型，所以在平时的学习过程中，数学教师一方面要帮助学生明确拟题目标，把握重难点，一方面要给予学生切实的具体指导，引导学生不断提高拟题能力。

【关键词】拟题目标  自主  仿拟  创拟

学习原本就是学生自我构建的体验，但是，教育教学过程中的各种练习、习题、复习、试卷等编写的工作似乎从来都由教师来完成。平时的教学过程中，如果我们能够给予学生必要的指导，他们也可以胜任这项工作，而且会收到超乎寻常的教学效果。

如何指导学生自编题目呢？不同的方式或角度又各有什么作用呢？

一、明确学习目标，深入理解学习重点

在学生自主编题之前，教师必须提出非常明确的目标，并且要让学生明白出题的知识依据，熟悉重点、难点。有了目标，就有了出题的方向，有了重点和难点，就有了出题的鲜明倾向性，避免盲目，不知所措。

同时学生自己最好要以题目的形式对学习目标进行解读，进而分析自己的学习是否达到了学习目标，是否透彻理解了学习的重点，突破了学习难点。因此，这就迫使他们必须要盘点先前的学习，及时排解疑难。而这样做无疑又鼓励了他们的学习行为，懂得梳理、总结知识，培养自主学习的能力。

二、寻找典例，积极进行变式研究

起初，学生可能并没有掌握拟题的一些适当的方法，这需要老师给予必要的指导。古人说：“授人以鱼不如授人以渔。”有了方法的引领，学生就会少走弯路，提高拟题的效率。

1.仿拟。即仿照教材或其他经典例题拟题。有现成的例子，学生就会感到拟题并不困难，能够提高拟题的兴趣，享受到拟题的成就感。

（1）仿形式。即完全仿照现成例子，只是改变必要的数据或转换相近的条件。这种拟题相对容易，大众化，具有普适性。

例如：拟题目标：角的平分线性质（探究、掌握作角平分线的方法和角平分线性质;提高综合运用三角形全等、角平分线等知识解决实际问题的能力）。

教材原题：

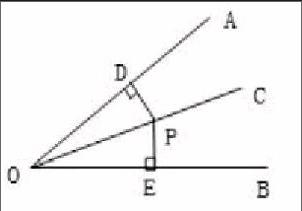
已知：∠AOC=∠BOC，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为点D、E。（如下图）

求证：PD=PE。

仿拟：

已知：如上图，∠AOC=∠BOC，点P在OC上，在OA上取D，连接PD，且使PD⊥OA。在OB上取E点，连接PE，使OD=OE。

求证：PD与PE之间是什么关系？PE是否垂直于OB？

分析：仿拟题目只是改变了部分已知条件，少了“PE⊥OB”，把它移到结论上，作为求证的目标;“求证”看上去虽然改变了，但是，实质上仍然是指向“PD=PE”“PE⊥OB”，即角平分线性质中“角平分线上的任何一点到角两边的距离相等”。很显然，这样拟题的难度明显要小一些，且能够在现成例题的基础上巩固对例题知识指向点的理解，不过，因为它缺乏明显的实质上角度的改变，即具有单向性的弊端，所以无法更全面地帮助学生理解知识概念。

2.创拟。即明显地变换不同的角度，创造性地拟制题目。或者针对原理、概念的某一构成元素设题，或者将结论变成条件，将条件变成结论拟题;或者将目标知识点、能力点与其他数学问题链接融合，整合拟题;或者将数学现成题目元素与应用情境联系起来拟题，等等。

“创”主要体现在创造性思维上，不是平面、线性的思维，而是多角、立体地运思，体现出良好的数学思维品质，彰显出“广阔性、灵活性、深刻性、独创性和批判性等”。学生天生就具有良好的想象力，这表现在数学上同样如此，只要稍加点拨即可。

例二：拟题目标：理解、运用三角形定理。

拟题思路：

（1）到角两边的距离都会相等的点，一定都在该角的角平分线上。

（2）三角形一个角的平分线，这个角平分线其对边所成的两条线段与这个角的两邻边对应成比例。

（3）三角形的三条内角平分线相交于一点。

（4）三角形是三条角平分线交汇的这一点到三条边的距离必定相等。

（5）一个新规划的交通枢纽涵盖火车站、高度公路、飞机场等三处主要实施，请你论证一下，能不能找到一个合适的地点，设置一处大型的公共汽车站，要求这座车站从距离上离三处主要设施最近。

（6）你能用正弦定理论证角平分线定理吗？可利用圆的知识（作三角形的外接圆）。