一种基于平均值模型的小型航空活塞发动机喷油MAP的快速标定及优化方法

刘晓凌（西安爱生技术集团公司陕西西安710065）

一种基于平均值模型的小型航空活塞发动机喷油MAP的快速标定及优化方法

刘晓凌
（西安爱生技术集团公司陕西西安710065）

利用平均值模型给某小型航空发动机建立了发动机进气模型，并用贝叶斯决策论的方法对该模型数据进行了修正，得到了在贝叶斯决策论下的最优估计，简单快速地得到了发动机的喷油MAP。试验证明该方法简单有效，大大缩短了电子燃油喷射系统设计开发周期。

平均值模型贝叶斯决策论标定活塞发动机

引言

活塞发动机具有体积小，重量轻，升功率高及结构简单等优点，在我国现役的无人机装备得到了大量的应用［1］。目前使用的活塞发动机中大都采用的是化油器的供油方式。化油器的供油方式技术成熟，使用方便，但随着发动机使用高度的增加，化油器的高空特性变差，发动机的空燃比严重偏离发动机的设计点，使得发动机动力性、经济性和环境适应性变差，影响无人机的使用性能。而发动机电子燃油喷射系统不依赖感应外界气压的方式工作，只要提供足够精确的MAP图，就可对发动机进行精确控制，提高发动机的使用性能。

然而在MAP图标定时，由于影响MAP图标定的影响因素多，使得采样的数据具有一定的随机性。要得到精确的MAP图，需要对试验发动机进行大量的标定工作，使得电喷系统的设计周期较长，开发成本较大。

本文通过对发动机采用基于平均值模型的方法快速得到试验发动机的MAP模型，然后通过贝叶斯决策论的方法对发动机的MAP进行修正，得到在贝叶斯决策下的后验风险最小的MAP模型。通过试验验证该方法简单可行，可快速获得较高精度的发动机MAP图。

1　活塞发动机平均值模型

活塞发动机的平均值模型最早是由Rasmussen在其博士论文中提出，经过多年的发展，最后由丹麦技术大学的Hendricks进行了系统的总结与整理，给出了完整的模型和通用表达式。发动机的平均值模型忽略了不同曲轴转角所对应发动机内部的缸内变化的细节，对各缸的工作状态进行了平均化处理，是一种基于时间平均值的控制模型。由于该模型具有较少的参数和较低的阶次，且具有较高的整体精度，并能够对发动机的动态响应进行模拟，因此在实际中得到了广泛的应用。

本文采用的试验发动机为总排量为0.99 L的四缸水平对置风冷二冲程汽油发动机。原发动机采用的是化油器式的供油方式，考虑到改造简单方便，该发动机采用了进气道喷射的方法进行改造。发动机的喷油量是根据进气量和最佳空燃比计算出来的，而采用节风门角度和转速可间接地计算发动机的进气量，可以通过平均值模型的建立得到以节风门角度和转速为自变量，喷油量为函数值的MAP图。

发动机进气管中的气体服从气体理想状态方程：

p1为进气管中空气的压力，V1为进气管中空气的体积，m1为进气管中空气的质量，R为气体常数，T1为进气管中空气的温度。进气管的体积V1和温度T1可视为常量，对公式（1）求导可得：

根据质量守恒定律，进气管中空气的质量流量为节风门处的空气流量和离开进气管进入燃烧室处的空气流量之差，因此有：

m˙at为节风门处的质量流量，m˙ap为进气管出口处的质量流量。

根据发动机平均值模型［2-3］

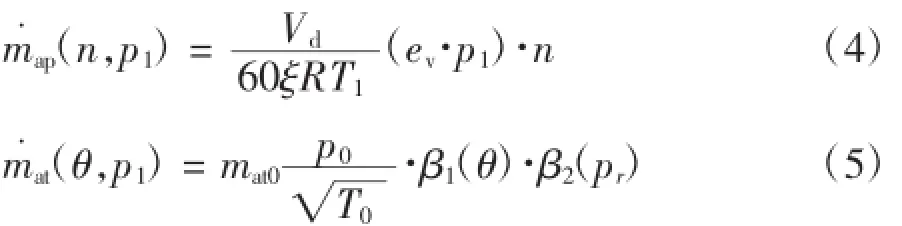
式中：p1为进气管内的压力，Vd为发动机排量，ξ为冲程数，ev为充气系数，n为发动机转速，θ为节风门角度，mat0为和发动机相关的常数，p0和T0为标准状况下的气压和温度，β1（θ）和β2（pr）为节风门角度θ和节风门后进气管压力p1和节风门前的大气压力p0的压比pr的函数。其中β1（θ）和β2（pr）分别为：

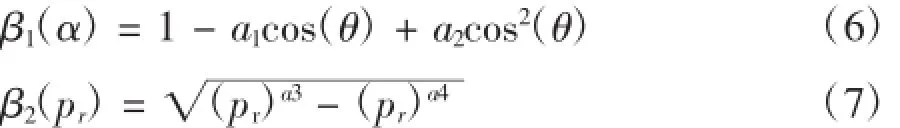
其中a1，a2，a3，a4为发动机相关的常数。

把（3）～（7）式带入（2）式，得到一个关于p1的一阶导函数。当发动机在某一工况稳定运转时，进气管的压力p1变化率为零，因此就可得到一个关于进气管压力p1、转速n和节风门角度θ的三元的非线性方程式

通过（8）式可得到发动机进气管气压、转速和节风门角度的三维MAP图。根据进气管气压值可得到实际循环的进气流量为：

然后根据空气流量和理想空燃比的关系算得燃油流量，如（10）式所示：

其中m˙f为每循环燃油流量，λ空燃比。然后根据喷油器流量特性可得到发动机的喷油MAP图。

把试验发动机的常数带入以上式子中得到的发动机的燃油流量、转速和节风门角度三维MAP图如图1所示。

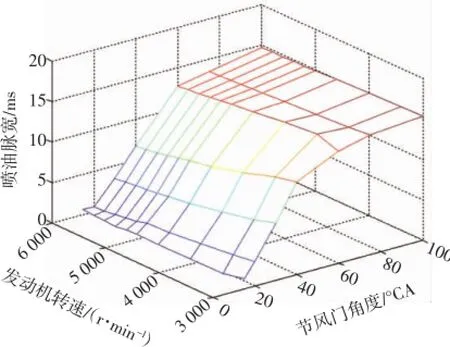
图1　发动机平均值法喷油MAP图

从计算数据以及图1可以看出当节风门一定时，随着发动机转速的增大，发动机喷油脉宽减小。当发动机转速一定时，随着节风门角度增大发动机喷油脉宽增大。

2　贝叶斯修正

从平均值模型得到的数据误差还较大，还不能直接用于发动机的控制，如实际使用还需要进一步的优化修正才能完全符合发动机的特性。MAP参数的优化有很多方法，本研究通过贝叶斯决策论的方法对通过平均值模型获得的数据进行进一步的修正。贝叶斯统计是基于总体信息、样本信息和先验信息进行的统计推断，它与经典统计学的主要区别在与是否利用先验信息。其中先验信息的分布是反映人们在抽样前对该总体分布的先期认识，通过对先验信息的利用可以大大提高统计推断的质量［4］。

本研究把通过平均值模型获得的数据看成喷油脉宽的先验分布π（T），T∈Θ，Θ为参数状态空间。把喷油脉宽T视为服从π（T）分布的随机变量。把通过抽样得到的样本X（t′1…t′n）看成是从总体分布p（t/T）中抽样的样本，则样本X的联合密度函数为：

该联合密度函数是综合了总体和样本的信息，是样本的似然函数。

由贝叶斯公式可得样本的后验密度函数为：

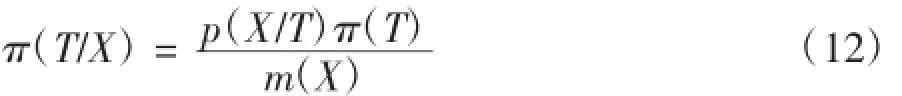
其中m（X）为边缘密度函数

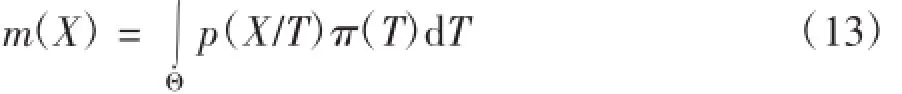
后验分布是反映在抽样后，新的样本对先验分布的修正，后验分布可以看作是用总体信息和样本信息对先验分布调整的结果。后验分布综合了总体信息，样本信息和先验信息，一切有关统计推断的参数信息都综合在后验分布中。要对推断参数做决策就从后验分布中提取。

在贝叶斯决策论中认为，每采取一种决策α对参数进行推断都是有损失的，该损失可用一个函数表达，该函数称为损失函数。在本研究中用L（T，α）表示损失函数，它表示当发动机的实际喷油脉宽为T时，采取决策α的损失，一般在统计中的决策α为一个参数的统计量估计。

把损失函数L（T，α）对后验分布π（T/X）求数学期望称为该参数采取决策α的后验风险，既：

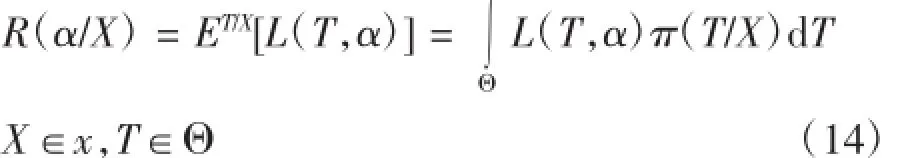
其中x为样本空间，Θ为参数状态空间。

从式（14）可以看出后验风险就是用后验分布计算的平均损失，它是样本X和决策α的函数，随着样本行动的不同后验风险也跟随着变化。

特别地当R（α′/X）=minR（α（x）/X）时，称α′为后验风险准则下的最优决策函数，称为贝叶斯决策函数。因此通过让后验风险达到最小的喷油脉宽参数T的估计是在贝叶斯决策论下的最优喷油脉宽，也即贝叶斯下的最优MAP。

特别当损失函数为平方损失函数L（T，α）=（T-α）2时，任一个决策函数α=α（x）的后验风险为

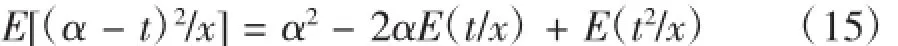
要使该式达到最小，当且仅当且αB（x）=E（α/x）时决策函数的后验风险达到最小，因此在平方损失下对喷油脉宽的最优贝叶斯决策估计也就是T的贝叶斯后验均值。本文既采用该平方损失函数进行了后面的参数优化修正。

3　试验验证

通过上述平均值模型方法和试验采样得到在发动机转速4 600、5 000和5 400 r/min时，不同节风门处喷油脉宽曲线如图2、图3和图4所示。

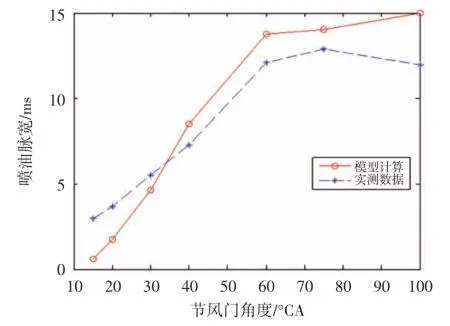
图2　4600 r/min时模型计算实测采样喷油脉宽

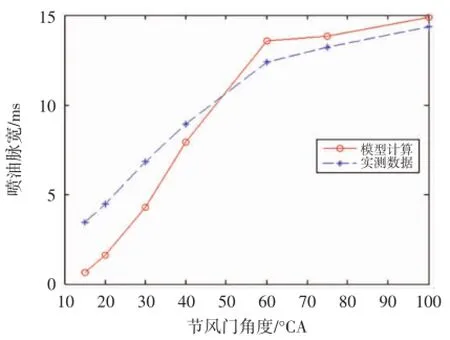
图3　5000 r/min时模型计算实测采样喷油脉宽

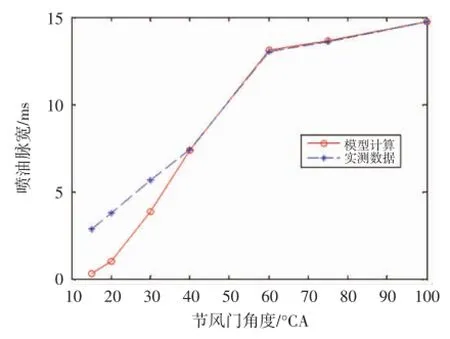
图4　5600 r/min时模型计算实测采样喷油脉宽

首先，从模型计算和实际采样数据图可以看出，通过平均值模型得到的数据在某些工况下和实测值比较接近，在某些工况下相差较远，但总体上理论模型计算值和实测值具有一致性，说明在设计电子燃油喷射系统的初期可以通过平均值模型的方法简单迅速的得到发动机喷油MAP，但必须通过其他方法对该MAP进行优化修正。其次由于影响发动机状态的因素有很多，且互相耦合，因此实测数据也具有一定的随机性，需要通过统计的方法校正偶然因素。

通过对上述两组数据采用贝叶斯决策论的方法进行数据优化修正。通过大量发动机喷油脉宽采样经验，本文采用了先验分布和总体分布都为正态分布分别为N（T1，τ2）和N（t，σ2），其中T1为先期标定MAP图中的喷油时间的数学期望，τ2和σ2为采样样本的方差。T1、τ2和σ2用喷油时间的矩估计获得，损失函数取为平方损失函数，则可得修正曲线如图5、图6和图7所示。

从修正曲线可以看出，贝叶斯决策论修正数据的方法对平均值模型计算的数据和实测数据进行修正是一种“平均”的修正，且该修正的后验风险最小，是贝叶斯决策论下的最优决策。通过在试验发动机上验证，该方法非常快速地得到了被试发动机的喷油MAP，且精度较高，能够满足发动机的控制要求，大大节约了燃油电子喷射系统的开发时间。

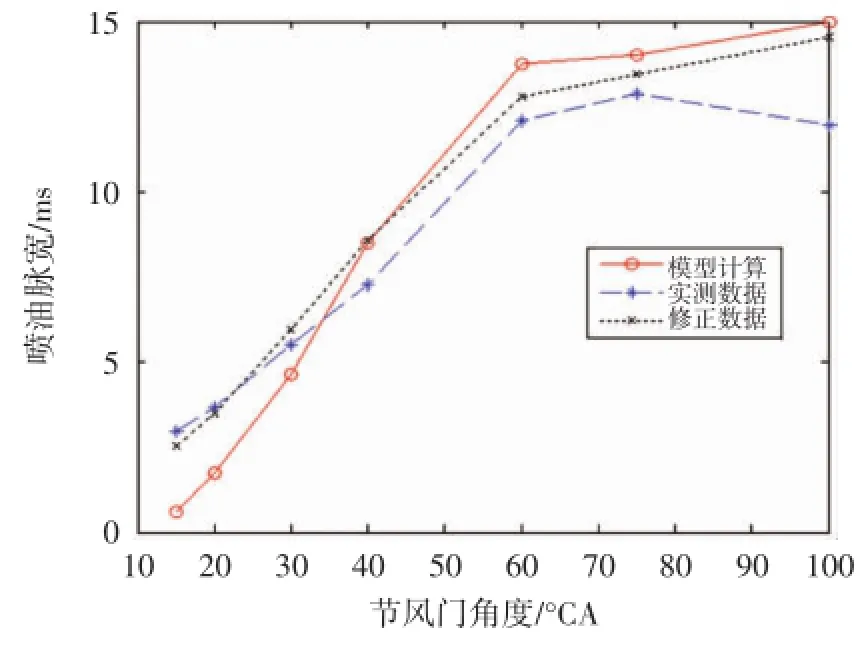
图5　4600 r/min时模型计算实测采样喷油脉宽

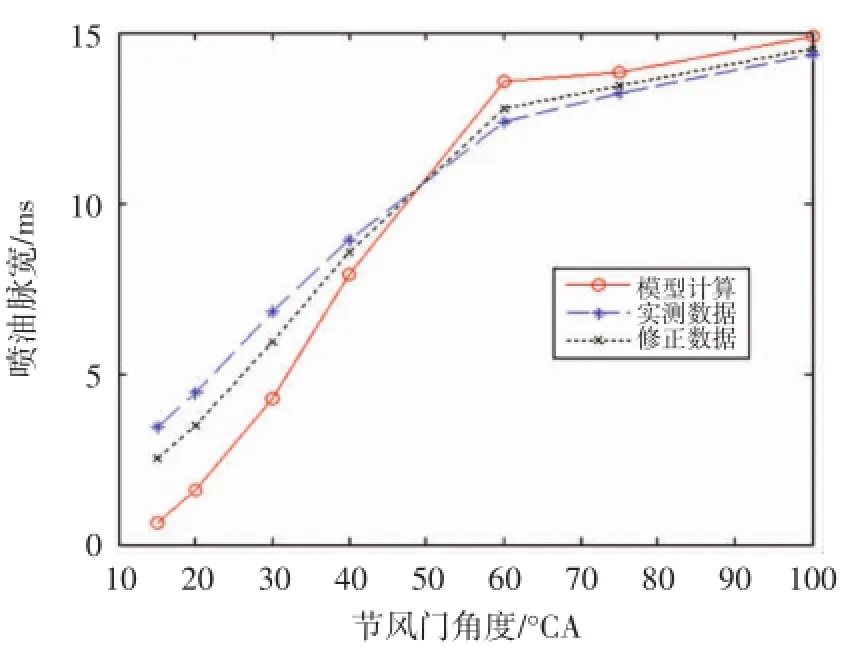
图6　5000 r/min时模型计算实测采样喷油脉宽

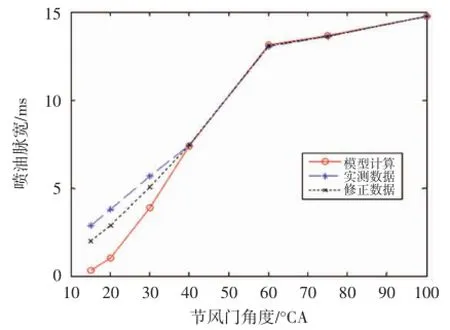
图7　5600 r/min时模型计算实测采样喷油脉宽

4　结论

本文通过采用平均值模型的方法简单快速地得到了被试发动机的基本喷油MAP图，然后又对该MAP采用贝叶斯决策论的方法进行了优化修正，通过该方法得到的MAP图在贝叶斯决策论下是最优的。通过该方法得到的MAP能较好的满足发动机电喷改造的需要，在实际试验中也得到了验证，大大缩短了电喷系统的改造周期，具有重要的理论和应用价值。

1李玉珍，马震，张学平.HS-700型发动机活塞的优化设计［J］.西安理工大学学报，2005，21（1）：86-90

2Santavicca Domenic A，Liou Deruh，North Gary L.A fractal model of turbulent flame growth［C］.SAE Paper 900024

3Hendricks Elbert，Chevalier Alain，Jensen Michael.Modeling of the intake manifold filling dynamics［C］.SAE Paper 960037

4师义民，许勇，周丙常.近代统计方法［M］.北京：高等教育出版社，2011

A Fast Calibration and Optimization Method of Small Aviation Piston Engine's Fuel MAP Based on Mean Value Engine Model

Liu Xiaoling
Xi'an ASN Technology Group Co.，Ltd.（Xi'an，Shaanxi，710065，China）

Based on mean value model，an intake model of the engine is established for a small aviation model.Also its data model has been modified by using Bayesian decision theory and optimally estimated with the theory，which result in a simple and fast way to get the fuel injection MAP of the engine.The experiment proves that the method is simple and effective and shortens the development periods of the design for electronic fuel injection system.

Mean value model，Bayesian decision theory，Engine calibration，Piston engine

TK411+.27

A

2095-8234（2015）04-0075-04

2015-05-19）

刘晓凌（1977-），男，工程师，主要研究方向为小型内燃机设计。