一种新的分数阶多卷波混沌系统及其随机性测试

车德欣　汤子隆

（广东金融学院）

一种新的分数阶多卷波混沌系统及其随机性测试

车德欣汤子隆

（广东金融学院）

提出一种新的分数阶混沌系统，通过设计非线性控制器，使其产生多卷波混沌吸引子。利用数值仿真方法给出8卷波混沌吸引子相图，并对该混沌系统的混沌序列进行NIST测试。结果表明，提出的混沌序列能较好地满足随机性测试。

分数阶混沌系统；多卷波；NIST测试

0　引言

分数阶混沌系统可以视为整数阶混沌系统在阶数上的推广，不仅具有整数阶混沌系统的所有特征，并且还具有整数阶混沌系统不具备的特征。分数阶多卷波混沌系统是近年来混沌研究领域取得的重要研究成果。多卷波混沌吸引子的相轨迹在不同吸引子之间跳变，卷波数量越多，跳变的随机性越强，使信息隐藏越隐蔽，这对信息加密具有十分重要的意义。分数阶多卷波混沌系统达到混沌状态时，其阶数是一个范围，而不是固定值；其密钥空间较整数阶更大，在混沌加密中具有重要的应用价值。在混沌加密领域，当前大部分研究都集中于整数阶混沌系统，较少使用分数阶[1-2]。Faieghi等人将分数阶混沌系统应用于图像加密领域，结果表明分数阶混沌系统具有更强的记忆功能和稳定性[3]。Alvarez等基于可扩展性混沌系统设计图像加密，表明分数阶混沌系统较整数阶更优秀[4]。张海英等人证明了分数阶Duffing系统作为密钥，其密钥空间较整数阶大很多[5]。朱伟等利用分数阶超混沌系统建立一种加密算法，其结果显示能有效低于选择明文供给，且性能优秀[6]。随着分数阶混沌系统在加密领域研究的不断深入，混沌序列的随机性测试也越来越引人关注。由于无法对随机性事件建立完整的数学模型[7]，因此，对混沌序列的随机性测试就显得尤为重要。本文提出一种分数阶混沌系统，并对其混沌序列的随机性进行测试。首先给出分数阶8卷波混沌系统的表达式，然后使用数值仿真给出其8卷波混沌吸引子相图，最后采用NIST测试证明其混沌序列的随机性。

1　一种新的分数阶8卷波混沌系统

本文提出一种新的基于分段型Lorenz系统的分数阶线性微分方程形式为

设计非线性混沌控制器，产生式(1)。设受控的分数阶Chen系统形式为

K( X )是非线性反馈控制器，其表达式为

其中，N=0, 1, 2, 3, …；i=1, 2, 3, …, N。

由式(2)，得参数Hi、Ei的递归公式为

式(3)中，各个参数的选取并不唯一。为使分数阶混沌系统能产生多翅膀混沌吸引子，只有设计合理的参数才能实现。

为产生多卷波的几何形状，需函数k3使分数阶混沌系统产生拉升与折叠效果，选取k3中各个分段函数的分段起点坐标值：

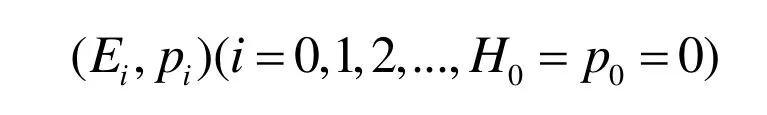
终点坐标值为

得到终点与起点坐标值满足以下关系：

首先计算on(n=1,2,3,...)，然后计算pn( n=0,1,2,...)，得on(n=1,2,3,...)与参数Hi、Ei的递归公式

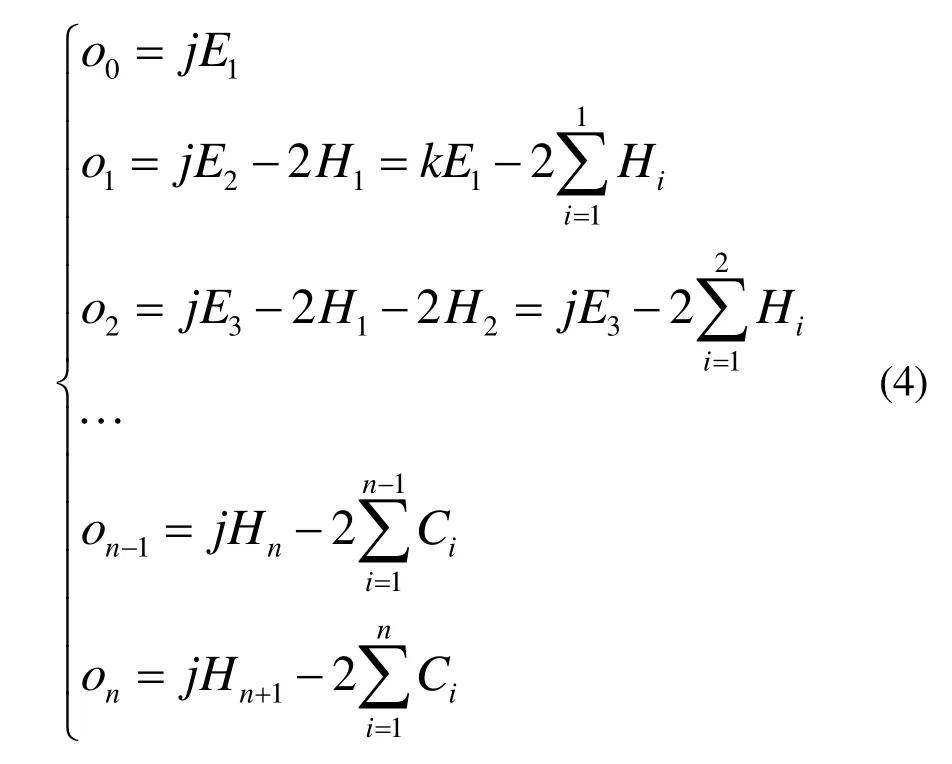
参数pn( n=0,1,2,...)的递归公式为

由式(4)与式(5)，得pn, on( n=0,1,2,...)的参数值为

选取k3中第1个区间宽度

则由式(2)与式(3)计算可得平衡点：

选取k3中分段线性函数终点(Ei, oi-1)与后一个线性分段函数起点(Ei, pi)之间的差满足：

为得到分数阶混沌系统的多卷波混沌吸引子，采用GL定义的分数阶积分进行计算，则可转换为

其中，e是步长；

将式(6)展开得

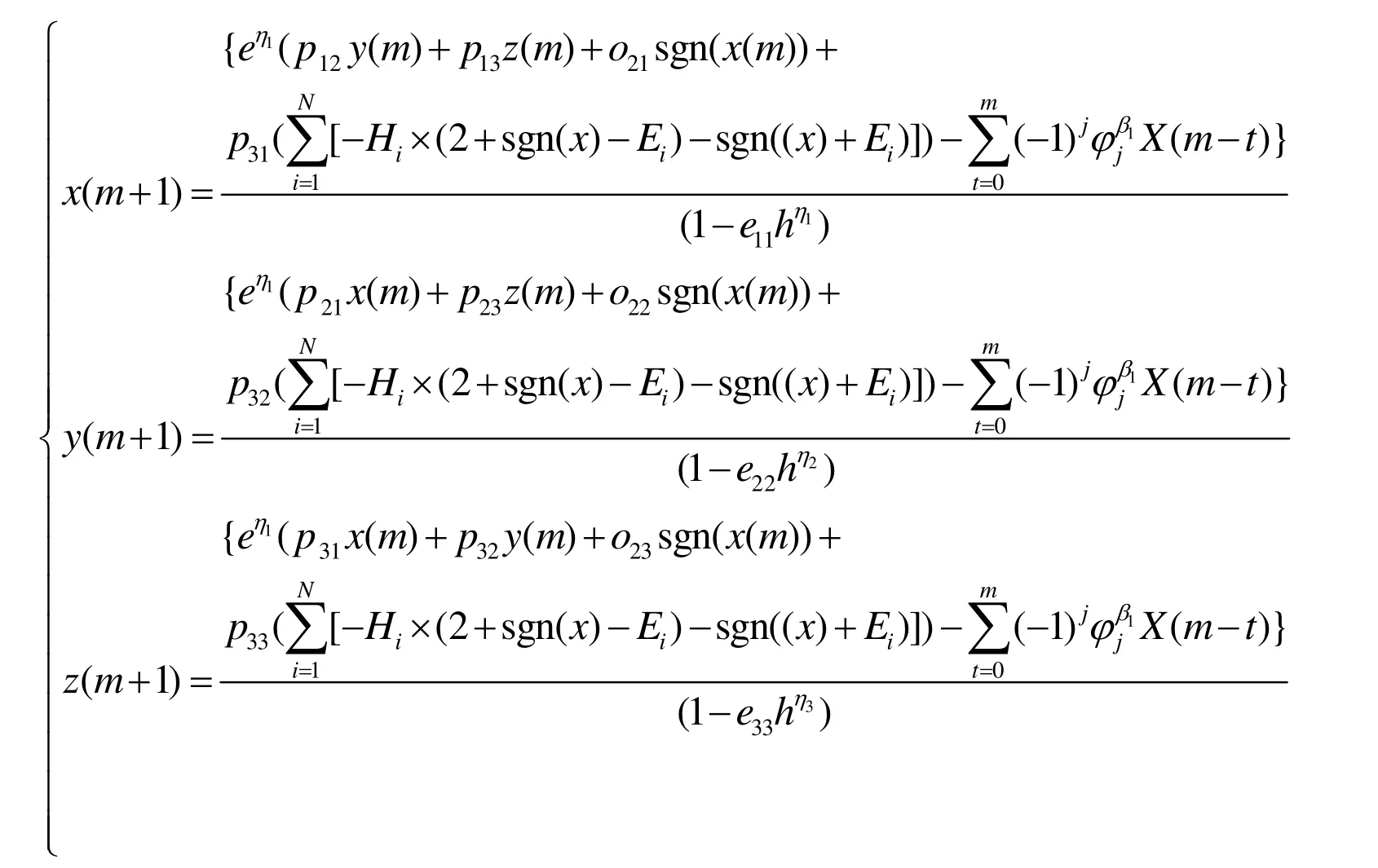
阶数η=(η1,η2,η3)=(0.9,0.9,0.9)，得

其中，a=0.5,b=0.09,c=2.6。

在k3中，设N=3, k=2.5, P=0.47，H1= H2=H3=0.228, E1=0.188,E2=0.36，得到2.7阶混沌系统8翅膀混沌吸引子如图1所示。

2　对分数阶混沌序列进行NIST测试

NIST随机性测试由美国国家标准技术研究院研发，其包含15种随机性测试手段，可从不同检验角度将被检测序列与理想随机序列进行对比，检验其偏离程度，是目前公认的比较好的随机性测试方法。NIST随机性测试的结果以P-value的值表示，令α∈[0.001,0.01]为显著性水平区间，当P-value≥α，表明该项测试能够通过随机性测试；否则为不通过，表明混沌序列不具备随机性。

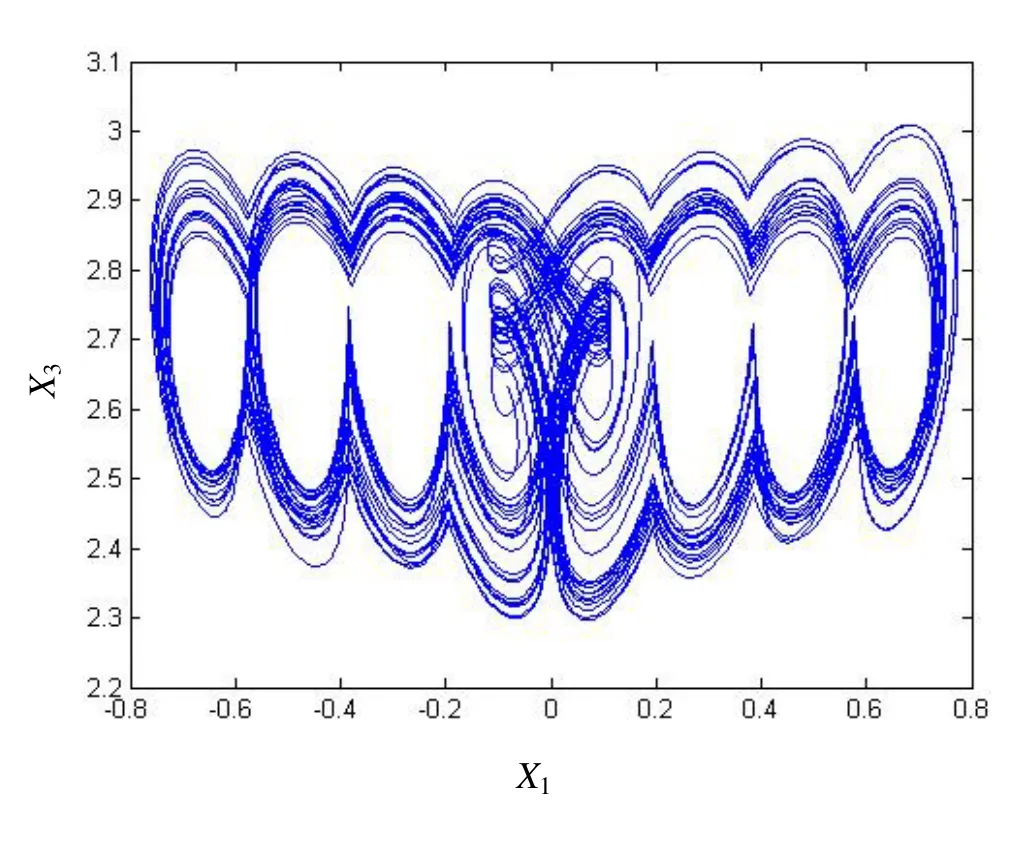
图1 分数阶8卷波混沌吸引子

对y序列进行NIST测试，其结果如表1所示。NIST随机性测试包含15个测试，分别为Frequency测试、BlockFrequency测试、CumulativeSums测试、Runs测试、LongestRun测试、Rank测试、FFT测试、NonOverlappingTemplate测试、OverlappingTemplate测试、Universal测试、ApproximateEntropy测试、RandomExcursions测试、RandomExcursionsVariant测试、Serial测试、LinearComplexity测试。C1-C10表示NIST随机性测试将[0,1]区间划分为10个子区间，然后分别计算每个子区间频数。P表示P-value，Value Proportion为通过计算显著性水平大于0.001的P值与混沌子序列的比值的数量。由表1可知，所有15个测试的P值均大于0.001。表明混沌序列通过了NIST随机性测试，本文所提出的基于分数阶多卷波混沌系统的混沌序列能够很好地满足随机性需求。

表1 NIST随机性测试结果

3　结论

本文提出一个新的分数阶多卷波混沌系统，利用数值仿真方法给出其8卷波混沌吸引子，并对提出的多卷波混沌系统所产生的混沌序列进行NIST测试。结果表明，本文提出的混沌序列能完全通过NIST测试，满足加密所需的随机性需求。

[1] 张兆祥,田沛,范瑾,等.基于分数阶傅立叶变换的图像加密研究[J].仪器仪表用户,2007,14(5):87-88.

[2] 王银花,柴晓冬,周成鹏,等.基于分数傅里叶变换的混沌图像加密方法[J].计算机工程,2007,33(12):172-174.

[3] Faieghi M R, Delavari H, Baleanu D. Control of an uncertain fractional-order Liu system via fuzzy fractional-order sliding mode control[J]. Journal of Vibraton and Control, 2012,18(9):1366-1374.

[4] Alvarez E， Fernández A, García P, et al. New approach to chaotic encryption[J]. Physics Letters A, 1999,263(s 4-6):373-375.

[5] 张海英,张卫,刘金梅,等.分数阶Duffing系统在图像加密中的应用[J].计算机工程与科学,2012,34(6):18-22.

[6] 朱伟,段文强,杨阳,等.基于分数阶超混沌系统的图像加密算法及安全性分析[J].重庆邮电大学学报:自然科学版,2012,24(4):501-506.

[7] 亓民勇,董金新,潘全科.信息安全中序列随机性测试系统的研究与设计[J].计算机工程与设计,2008,29(6):1453-1455.

A New Fractional-Order Multiwing Chaotic System and It’s Randomness Test

Che DexinTang Zilong
(Guangdong University of Finance)

In this paper, a new fractional-order chaotic system is proposed, which can generate multi-scroll chaotic attractors by designing a nonlinear controller. Using the numerical simulation method, the phase diagram of the 8-scroll chaotic attractors has benn given. Then, the chaotic sequence of the chaotic system pastNIST test. The results show that the chaotic sequences can satisfy the randomness test.

Fracional-Order Chaotic System; Multi-Scroll Attractors; NIST Test

车德欣，男，1988年生，本科，初级，主要研究方向：软件工程。E-mail: 164533507@qq.com