加速寿命试验在产品变工况下退化数据归一化中的应用研究

甘祖旺

（昆明船舶设备试验研究中心）

加速寿命试验在产品变工况下退化数据归一化中的应用研究

甘祖旺

（昆明船舶设备试验研究中心）

基于加速寿命试验中紧缩失效阈值和加速因子的计算方法，提出虚拟失效的概念，通过建立工况折合因子关于性能退化量的函数关系，并利用工况折合因子对每一性能退化量所对应的时间进行修正，达到对产品不同工况下性能退化数据的归一化处理，为变工况下的实时可靠性评估与寿命预测提供技术支撑。

加速寿命试验；虚拟失效；工况折合因子；数据归一化

0　引言

近年来，基于性能退化分析的产品实时可靠性评估与预测技术研究得到了广泛关注[1-4]。该研究克服了传统的可靠性评估与预测通常以一类产品为对象，通过对产品样本做统计分析来推断产品总体的寿命，而无法预测单个特定设备或系统寿命的缺点。现有方法都是利用同一工况下的性能退化数据进行评估与预测，并没有考虑到实际运行中工况很难保持唯一，且这种同一工况的处理方法往往忽略了对产品退化数据的合理挖掘与充分利用，从而影响其在实际工况下的准确性。产品变工况下的退化数据归一化利用，成为制约变工况下实时可靠性评估与预测的瓶颈。为此，本文针对工况变换的问题，借鉴加速寿命试验中的相关思想，提出工况折合因子建模方法，实现产品变工况下的退化数据归一化。

1　加速寿命试验中加速因子统计推断方法

1.1加速寿命试验的基本假设

目前加速寿命试验中的基本假设[5]概括起来主要有以下4条：

1) 寿命分布同族性假设，在所有加速应力水平（S1＜S2＜…＜Sk）和正常使用应力水平S0下，产品的寿命服从同一分布函数族；

2) 分布参数约束假设即失效机理一致性假设，以威布尔分布为例，在工程实践经验总结的基础上，往往假设“形状参数反映威布尔分布的失效机理，形状参数恒等约束是威布尔分布场合加速寿命试验失效机理一致性的充要条件”[6]；

3) Nelson统计模型假设，若产品在应力水平Si作用时间ti内的累积失效概率Fi（ ti）与产品在应力水平Sj作用时间tj的累积失效概率Fj（ tj）相等，即Fi（ ti）=Fj（ tj），则产品在两种情况下的寿命退化累积量相同；

4) 加速模型假设，产品在所有试验应力水平下的失效机理与正常使用条件下的失效机理保持一致。

1.2加速因子的定义及计算

根据Nelson的累积失效模型，可对加速因子做如下定义：若产品在应力水平Si和Sj下分别作用时间ti和tj的累积失效概率相同，即Fi（ ti）=Fj（tj），则称为应力Si相对于应力Sj的加速因子。该定义实际上阐明了试验数据的寿命退化累积等量折算的基本原理。如果产品在应力水平Si作用下试验了时间ti，则在应力水平Sj作用下达到相同退化累积的等效试验时间tj由下式确定：

2　虚拟失效

2.1虚拟失效阈值

产品的失效机理可分为过应力机理和耗损型机理两大类[7]。对于过应力机理，当外界的应力超过产品自身的强度时产品失效；当外界的应力小于产品自身的强度时产品正常，这种失效称为突发性失效。对于耗损型机理，外界应力并不会造成产品立即失效，而是造成一定的损伤，使产品性能逐渐退化，这种失效并不是产品完全失效，而是产品性能无法达到使用要求，也称为“软失效”[1]。

由上述退化型失效的定义可知，表征产品退化的性能退化特征量首次达到失效阈值的时间为产品的失效时间，因此产品的失效时间与监测性能退化特征量的失效阈值密切相关，失效阈值的不同意味着对产品功能要求也不同。从物理意义上来说，失效阈值也是产品的一个性能退化特征量。基于此，本文提出虚拟失效阈值的概念。

虚拟失效阈值：对于递减（递增）退化型失效的产品，当其性能退化特征量达到某一大于（小于）产品实际失效阈值的特定数值时，假设该产品失效，该值即为产品的虚拟失效阈值。图1以递减退化型失效产品为例，l0是在额定工况下产品实际失效阈值。对于递减退化失效产品，失效阈值越大，意味着对产品有越高的功能要求，也意味着产品越容易发生因不满足功能要求导致失效，其寿命也越短。采用紧缩失效阈值的方法，假设产品在性能退化特征量达到l1或l2时失效，l2>l1>l0，则称l1或l2为产品该性能退化特征量的虚拟失效阈值。根据虚拟失效阈值达到的失效称为虚拟失效，产品的性能退化特征量首次达到虚拟失效阈值的时间为产品的虚拟失效时间。

2.2虚拟可靠度函数

可靠度的定义为：产品在规定的条件下和规定的时间内，完成规定功能的概率。产品的可靠度函数则是可靠度关于时间的函数：其中，R(t)为可靠度函数；ξ为产品故障前的工作时间；t为规定的时间。

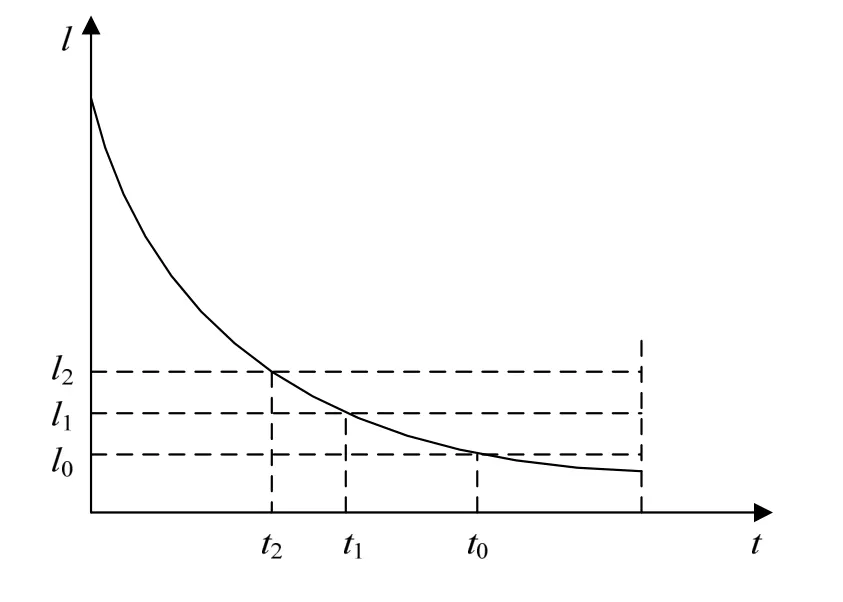
图1　虚拟失效阈值

对于退化型失效产品，上述可靠度定义中的规定功能即指产品性能退化特征量未达到失效阈值。因此，当引入虚拟失效阈值时，退化型失效产品的虚拟可靠度定义为：产品在规定的条件和时间内，性能退化特征量未达到虚拟失效阈值的概率。依定义可知，产品的虚拟可靠度是时间的条件概率函数，表示为

其中：l 为虚拟失效阈值；R（ t, l）为虚拟失效阈值l对应的虚拟可靠度函数；ξ为产品性能退化特征量达到l前的工作时间；t为规定的时间。

从上述可靠度和虚拟可靠度的定义可以看出，对于退化型失效的产品，虚拟可靠度是可靠度这一概念的延伸，两者之间唯一区别在于失效阈值的不同，即对产品功能要求的不同，而没有本质上的区别。因此，可以引入一些关于可靠度方面的概念和方法。

3　变工况条件下的数据归一化建模

3.1假设前提及计算准则

为得到工况折合因子关于性能退化特征量的函数关系，本文主要遵循以下3个假设前提：

1) 对于产品而言，工况的改变只是改变了产品的退化速率，而不影响产品的失效机理，因此，假设在不同工况下，产品的失效机理不变；

2) 产品的寿命分布一般只与产品的类型有关，而与运行的工况以及失效阈值的大小无关，如电子产品服从指数分布，轴承服从两参数威布尔分布等，因此，假设在不同工况不同失效阈值下，产品寿命服从相同分布族；

3) 根据Nelson假设，产品的剩余寿命仅依赖于已累积的失效和所属的工况，而与累积方式无关。

在加速寿命试验加速因子的计算中，数据折合准则是可靠度不变，即在某一应力下，某一时刻的可靠度应与另一应力下折合后对应时刻的可靠度一致。将其进一步引申，得到本文中工况折合因子的计算准则：对于相同的虚拟失效阈值，产品在某一工况下某一时刻的虚拟可靠度应与另一工况下折合后对应时刻的虚拟可靠度一致。假设产品的虚拟失效阈值为Ln，在工况一和工况二下的虚拟可靠度函数分别为R1（ t）和R2（ t），其中可靠度函数形式相同，基于上述假设可以得到产品在虚拟失效阈值Ln下，工况一对工况二的工况折合因子：

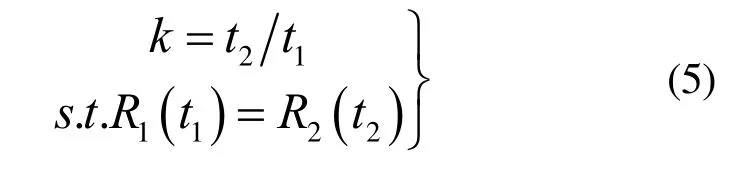
即在工况一下性能退化量达到Ln所需的时间t1，相当于在工况二中运行了时间t2=kt1。由式(5)可知，想要获得性能退化量Ln对应的工况折合因子k，需要已知2个工况下虚拟可靠度函数的参数。

3.2工况折合因子建模

以指数分布为例，若某一产品在标准工况（工况一）下，对应虚拟失效阈值Ln的虚拟失效分布服从指数分布，分布参数为μ1。利用在工况一中运行得到的试验样本数据并结合参数估计方法可以得出μ1的值。因此可得到工况一下对应虚拟失效阈值Ln的虚拟可靠度函数为

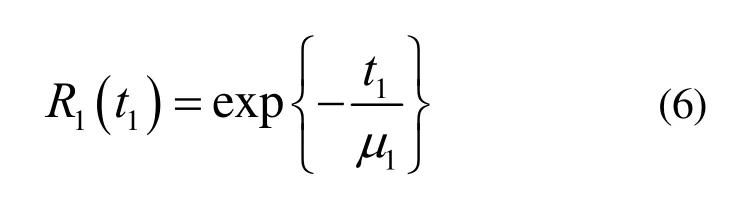
由假设前提2)，在不同工况下，产品寿命服从相同分布族，产品在工况二下对应虚拟失效阈值Ln的虚拟失效分布也服从指数分布。利用在工况二中运行得到的试验样本数据，可以估计得到工况二中的虚拟失效分布的参数μ2。则工况二下对应虚拟失效阈值Ln的虚拟可靠度函数为

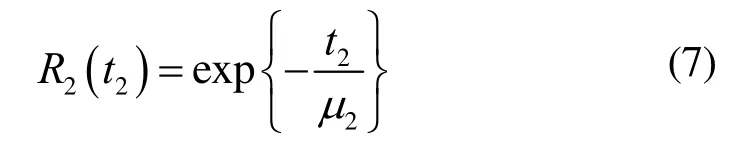
由R1（ t1）=R2（ t2）可得，在性能退化量Ln（即虚拟失效阈值）下，工况二对应工况一的工况折合因子为

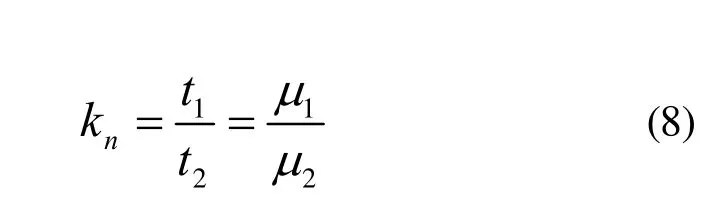
通过上述方法可得到一系列（Li, ki）,i=1,2,…。采用多项式拟合的方法可建立工况二对应工况一的工况折合因子与性能退化量的函数关系k = f (L)，从而可对性能退化数据进行归一化。

上述分析都是基于失效时间服从指数分布这一假设，指数分布中只含有尺度参数，因此，其工况折合因子的计算较为简单。若产品的失效时间服从“形状—尺度分布”，在计算工况折合因子时需要根据3.1中的假设前提1)，假设其形状参数m不变。

3.3性能退化数据归一化

利用3.2节建立的工况折合因子模型，可对性能退化数据进行归一化处理，性能退化数据进行归一化流程图如图2所示。

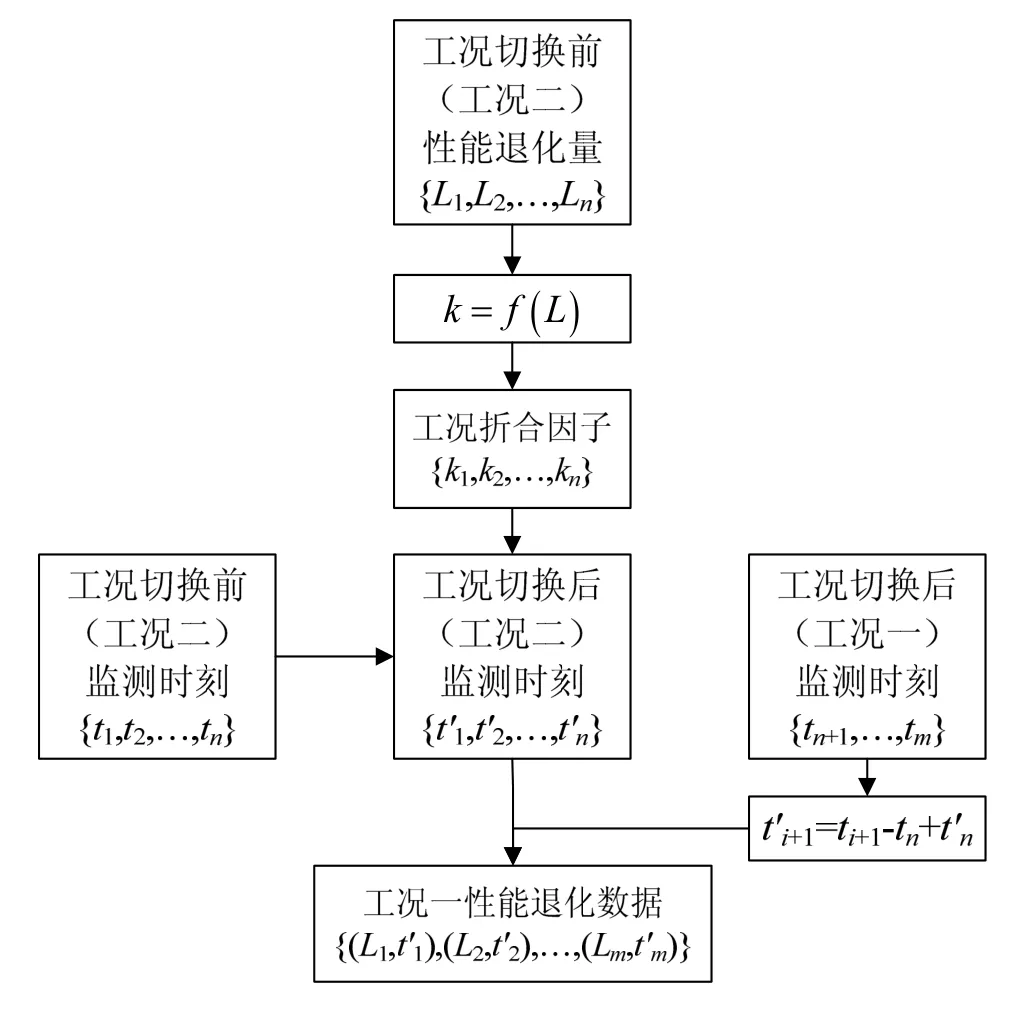
图2 性能退化数据进行归一化流程图

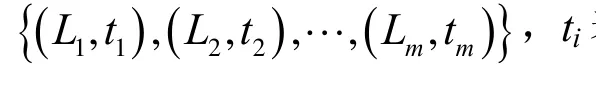
为了能将前后所处工况不一致的退化数据用于实时可靠性评估与寿命预测，需要将性能退化数据归一化到工况一中，具体分为以下3步：

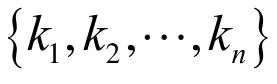
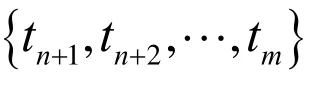
4　实例分析

本文利用NASA PCoE研究中心提供的3组锂离子电池的性能退化数据[8]，对所提出的变工况下性能退化数据归一化方法进行验证。第一组数据包括4个电池，电池运行的环境温度为24℃；第二组数据包括3个电池，电池运行的环境温度为43℃。在每一周期结束时测量电池的容量，并将其作为电池的性能退化特征量。2组电池的容量如表1、表2所示。

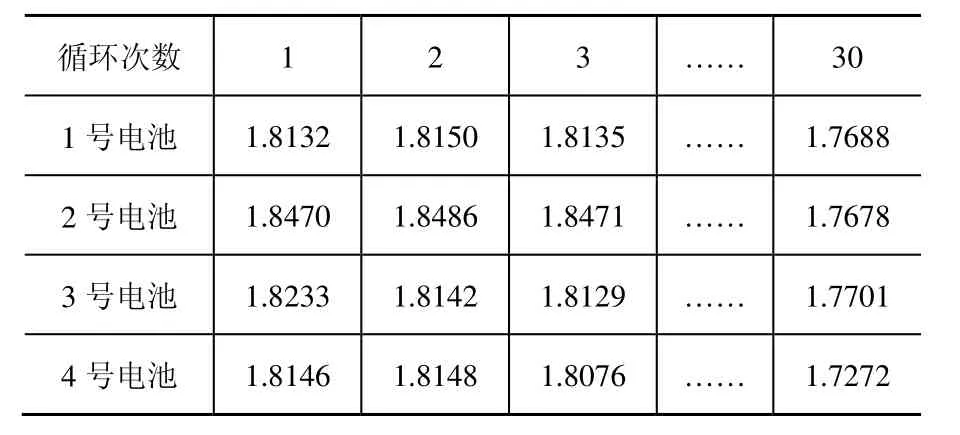
表1 第一组电池（24℃）　（单位：Ah）

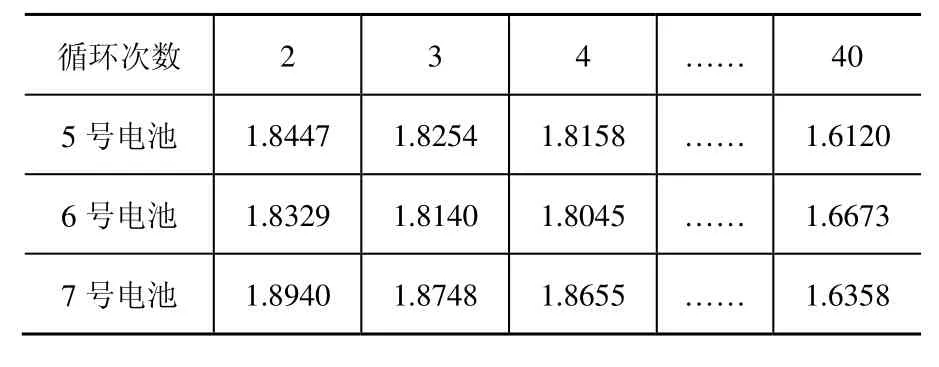
表2 第二组电池（43℃）　（单位：Ah）

第3组数据为前后不同温度（变工况）下的锂离子电池的退化数据，如表3所示。其中第12次循环之前（包括第12次循环）的运行环境温度为24℃，13~47次循环的运行温度为43℃。

表3 锂离子电池变工况下性能退化数据

为得到第一、二组中各电池相同性能退化量所对应的时间，需要对7个电池进行重采样。以1号电池为例的原始性能退化量数据如图3所示。

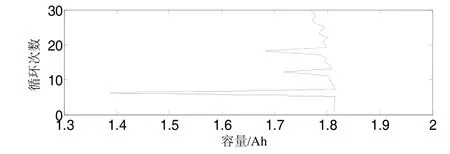
图3 1号电池的原始性能退化量数据

为得到性能退化量为{1.814，1.813,…,1.771}所对应的时间（即循环次数），需要对性能退化数据进行多项式曲线拟合。如图3所示，1号电池的性能退化数据含有3个奇异点，在拟合之前应将3个奇异点剔除，最终利用拟合得到的多项式函数可以得到重采样之后的数据，如图4所示。

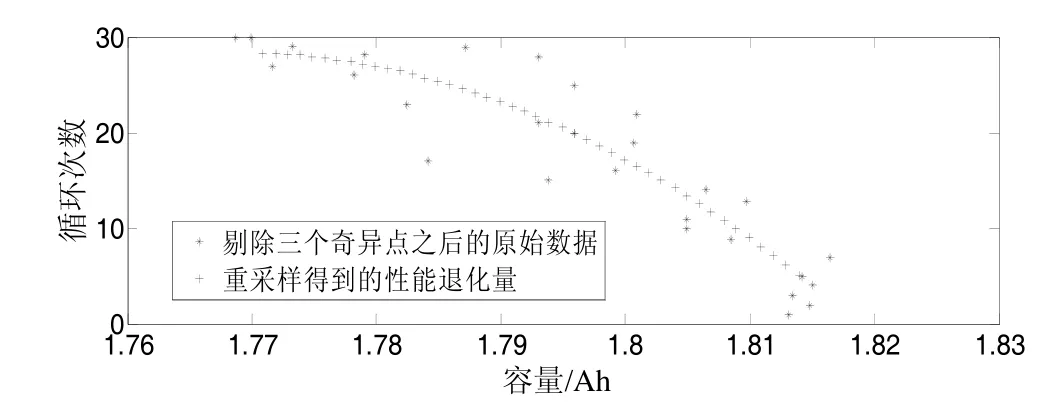
图4 1号电池的性能退化原始数据及重采样数据

利用上述同样的方法对其他6个电池的性能退化数据进行重采样，结果如表4、表5所示。

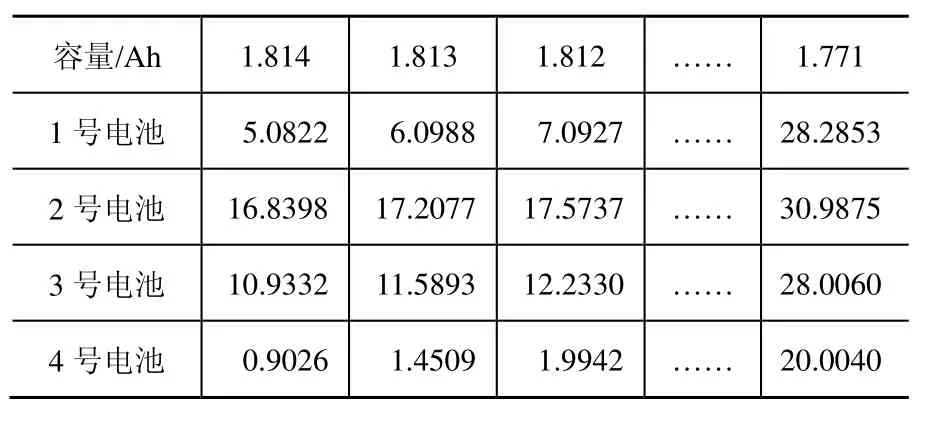
表4 第一组电池重采样数据（24℃）

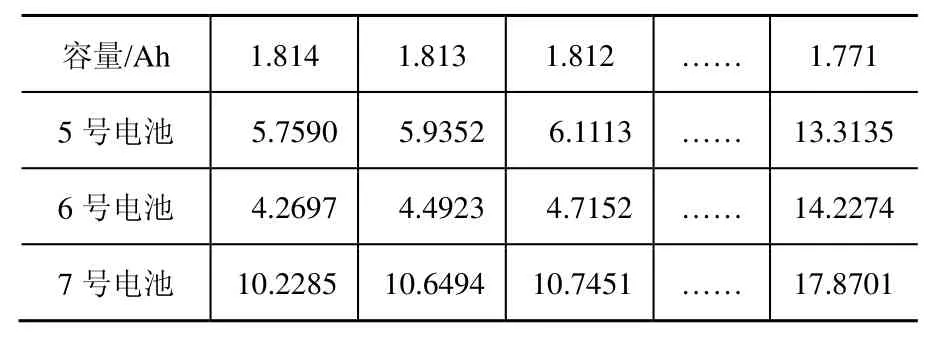
表5 第二组电池重采样数据（43℃）

由于电池的寿命一般服从指数分布，因此对2组数据相同容量的时间分别进行指数分布拟合，得到各容量对应的指数分布参数μ的值，如表6所示。

表6 指数分布参数

由式(8)，可得到在各容量（性能退化量）下工况二（43℃）对应工况一（24℃）的工况折合因子，如图5*线所示。利用多项式拟合可得到工况折合因子对应容量的函数关系：

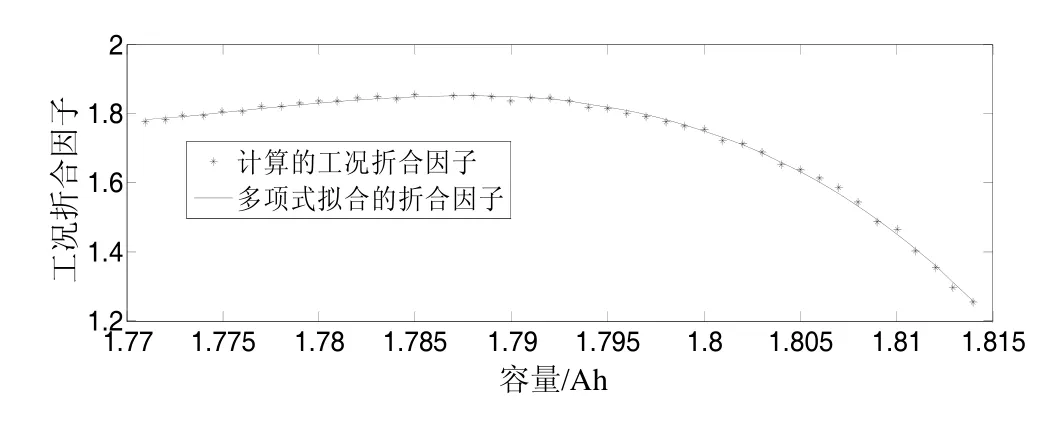
图5 工况折合因子对应容量的函数关系

由于上述工况折合因子对应43℃工况的数据向24℃工况进行折合，而第3组的电池退化数据需要将24℃工况中的数据向43℃进行折合。因此，将表3中第5~12个循环对应的容量代入式（10）并取其倒数，得到24℃工况中的数据向43℃进行折合所需的工况折合因子，如表7所示。

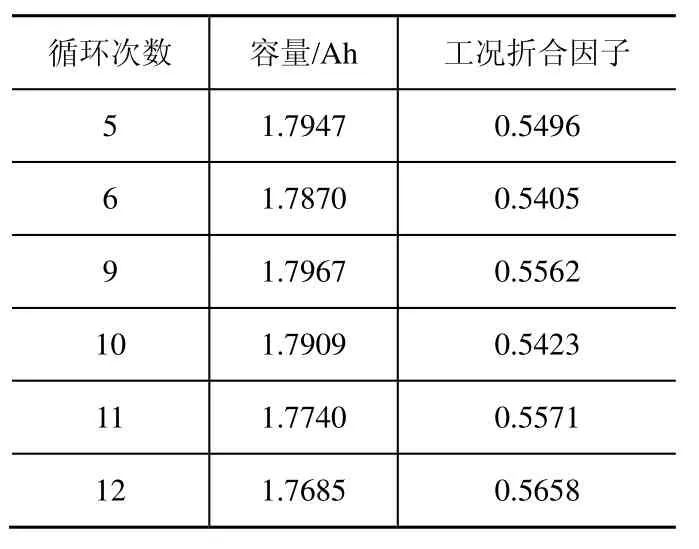
表7 工况折合因子

根据得到的工况折合因子及图2所示的性能退化数据归一化方法，可得到归一化后运行工况为43℃的性能退化数据。由于锂离子电池以一次充放电为一个周期，因此对24℃运行的折合后数据进行重采样，并对公式(9)中的tn＇四舍五入，取其整数为7次，最终的归一化后的性能退化数据如表8所示。

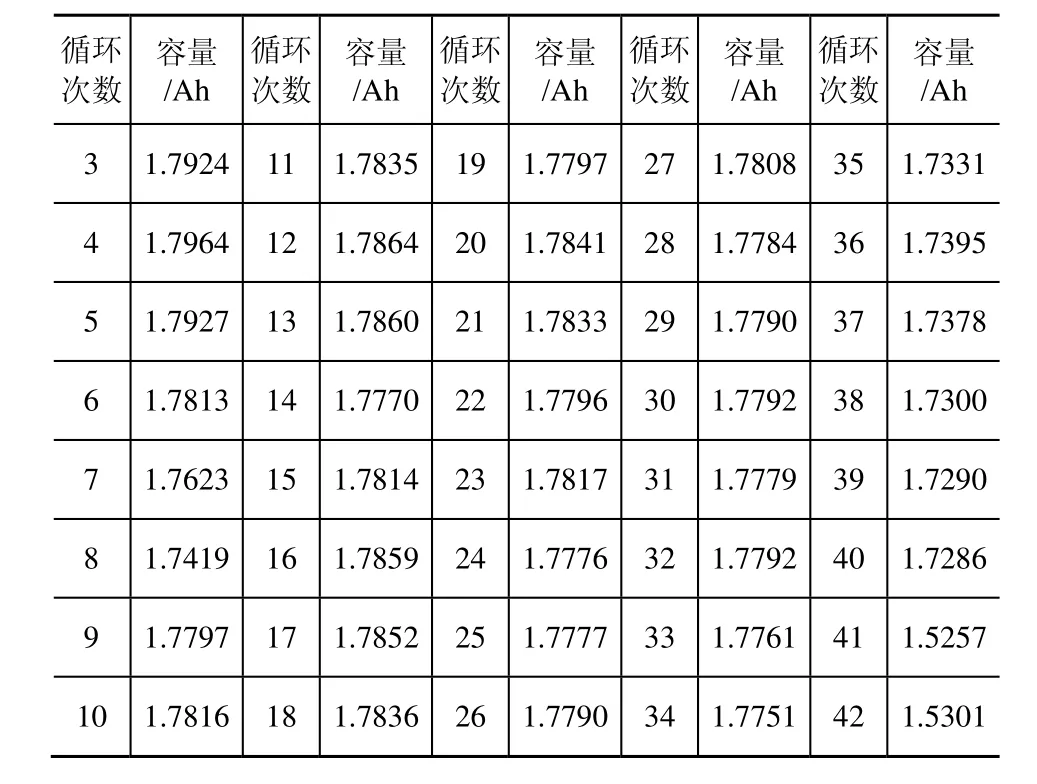
表8 归一化后运行工况为43℃的电池性能退化数据

5　结语

本文将加速寿命试验的思想应用到产品变工况条件下性能退化数据归一化的研究中。首先，阐述加速寿命试验加速因子的统计推断方法；其次，在分析耗损型失效的基础上提出了虚拟失效的概念；然后，基于加速寿命试验加速因子和虚拟失效的相关理论，提出一种基于工况折合因子的退化数据归一化方法；最后，通过NASA PCoE研究中心的3组锂电池性能退化数据对该方法进行了验证。结果表明：该方法能够有效实现不同工况下产品性能退化数据向同一工况的折算转换，从而为变工况下的产品实时可靠性评估与寿命预测提供了有力的技术支撑。

[1] Meeker W Q, Escobar L A, Lu C J. Accelerated degradation tests: modeling and analysis [J]. Technometrics, 1998, 40 (2): 89-99.

[2] Lu C J, Meeker W Q. Using degradation measures to estimate a time-to-failure distribution[J]. Technometrics, 1993, 35 (2): 161-174.

[3] Tseng S T, Tang J, Ku I H. Determination of burn-in parameters and residual life for highly reliable products [J]. Naval Research Logistics, 2003, 50(1): 1-14.

[4] 邓爱民,陈循,张春华,等.基于性能退化数据的可靠性评估[J].宇航学报,2006,27(3):546-552.

[5] 张春华.步降应力加速寿命试验的理论和方法[D].长沙:国防科学技术大学,2002.

[6] 孙利民,张志华.Weibull分布下恒定应力加速寿命的试验分析[J].江苏理工大学学报:自然科学版,2000,21(4):78-81.

[7] Dasgupta A, Pecht M. Material Failure Mechanisms and Damage Models [J]. IEEE Transactions on Reliability, 1991, 40(5):531-536.

[8] Saha B, Goebel K (2007). "Battery Data Set", NASA Ames Prognostics Data Repository,[EB/OL].http://ti.arc.nasa.gov/ project/ prognostic-data-repository, NASA Ames, Moffett Field, CA.

Study on the Data Normalization of Product Degradation under Variable Operating Conditions Utilizing the Concepts from Accelerated Life Tests

Gan Zuwang
（Kunming Shipborne Equipment Test & Research Center）

Based on the tightening failure threshold and acceleration factor learned from accelerated life tests, this study first proposes the concept virtual failure. Then the function of conditions conversion factor relating to the performance degradation measure is constructed to revise the time corresponding to the performance degradation measures, and to realize the degradation data normalization under variable operation conditions. The proposed method can provide technical support for the real-time reliability assessment and life prediction. Finally, the feasibility and efficiency of this method is validated by the NASA PCoE li-ion battery dataset.

Accelerated Life Test; Virtual Failure; Conditions Conversion Factor; Data Normalization

甘祖旺，男，1990年生，硕士研究生，主要研究方向：可靠性与环境工程。E-mail: ganzw20080920@163.com