引领学生亲历数学意义的建构过程
2015-10-21王志南
王志南
教学中常常有这样的现象:某一类型的题目讲了多遍,也练过多次,可是学生还是反复地出错。此时,大多数教师的应对方法是精讲精练,让学生在实战中积累解题经验。然而,即便如此,部分学生仍不能从本质上理解题目的内涵,掌握解题的方法和策略。深入分析上述现象,学生之所以出错,是因为他们没有真正理解数学问题的内涵,未能从本质上分析数学问题。那么,教师如何引导学生让知识和方法“生根”,让“数学思维的脚印”踏得更深呢?
其实,在解决许多陌生或复杂的问题时,人们往往不急于寻找解决问题的方法和路径,而是向后退一退,回到问题情境的初始状态,这样就更容易发现和理解问题的本质,寻获解决问题的突破点。
一、 动手操作,亲历实践中寻获数学规律
在五年级上册的期末测试中,有这样一道题:王大爷用12米长的栅栏靠墙围成一个长方形羊圈(如图1),如果每条边的长都取整米数,一共有多少种不同的围法?所围的长方形面积最大是多少?
从测试数据的分析来看,参加测试的所有学生中,本题得满分的占总人数的32.1%,全错的占总人数的48.3%。而错误的原因在于,许多学生未注意到条件中的“一面靠墙”,直接将12米当成长方形周长,除以2后列举长和宽。事实上,这道习题曾在课后练习和单元测试卷中都出现过,这样看来,做过两次后学生再次遇到仍未能正确地分析和解答,说明这些同学并没有真正理解问题情境的含义,未能真正掌握解决问题的方法。
罗杰斯说:“真正能够影响一个人的行为的知识,只能是他自己亲身经历并加以同化的知识,凡是可以教给别人的结果性知识相对来说都用处不大。”那么,如何引领学生回到原点,从本质上理解问题情境,进而避免认知上的偏差和失误呢?笔者在展开“围篱笆问题”的教学时,为了让学生真正理解问题情境,设计了让学生“用火柴棒围长方形”的操作活动,先让学生用12根火柴棒围长方形,发现围长方形时要先求出长和宽的和,再依次列举。在教学“一面靠墙围长方形”时,再次让学生用火柴棒摆,并引导学生思考和比较:①一面靠墙围篱笆,先要确定哪条边?为什么?②共有几种围法,你是怎样有序地围的?③比较“直接用篱笆围长方形”和“一面靠墙围长方形”,你觉得在解题思路上有怎样的不同?通过操作、思考、比较和交流,学生发现:“一面靠墙围长方形”必须先确定“需要围两条边的其中一条”,从1米想起,依次列举。如果先确定“只需要一条边”的那条边,另一边就会出现小数,列举起来不方便。两题的不同之处在于,前者12米是长方形的周长,而后者12米是一条边加另两边的长度和。
显然,基于学生动手实践的数学学习,让学生对“如何围长方形”有了更丰富的活动经验和更深入的理解。同时,值得一提的是,我们要避免让操作活动沦为“表层的动手操作”,而应引导学生在操作中展开数学思考、比较和发现,获得“用篱笆围长方形”的活动经验,在活动中感悟和体验,进而寻获深刻的、富有意义的内在规律。
二、 构画草图,数形结合中理解数学本质
画图作为学生数学学习的基本策略,不仅可以帮助学生理解题意,解决问题,还可以借助画图,回到问题情境的初始状态,让学生在数与形的结合中直抵数学问题情境的“内核”,洞察数学本质。而在数学教学中,许多教师往往习惯于引导学生进行抽象的数学思考,而忽视画图这一基本策略的存在,如果这样,也就不难理解为什么有的学生面对陌生问题情境时会束手无策了。如学习“公倍数和公因数”后,学生遇到如下的题目,内心世界就开始纠结万分,无从下手了。
把一张长24厘米、宽18厘米的长方形纸剪成边长是整厘米且同样大小的正方形纸没有剩余。最多可以剪多少个,最少呢?
学生之所以难以找到解题的突破口,在于学生在解决“公倍数与公因数”的实际问题时,习惯于从题目中的“最大”或“最小”来确定要找的是最大公因数还是最小公倍数,而此题中,同一问题情境中既要求“最多剪多少个”,又要求“最少剪多少个”,学生就感到为难了。
与题目中抽象数量关系的理解相比,构画草图有其独特的优越性,以“数学图像”勾勒出“智力图像”,让思维不再抽象,而是具体可视。教学中,我们不妨引导学生放慢思维的脚步,根据题意构画草图(图2),结合草图来思考小正方形的边长与长方形的长、宽分别有怎样的关系?也就是长方形长与宽的公因数;进而再来思考:最多可以剪多少个,选怎样的公因数? 最少剪多少个,选怎样的公因数?
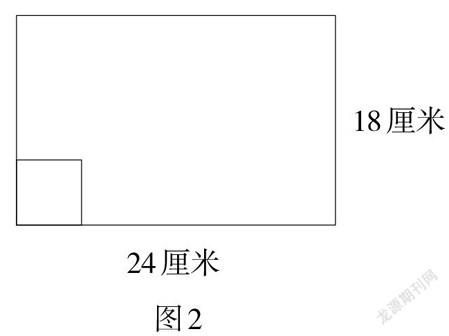
事实上,画图作为一种基本的数学分析方法,教师应重视学生画图习惯的养成和内化,要使之成为学生分析问题时自发的意识和习惯。苏教版教材四年级下册也特意安排了“画图策略”的教学,引导学生用画线段图、平面图等方法理解题意、解决问题。然而,学生在面对难以理解的问题时,往往没有自觉构画草图的意识,或者觉得无从画起。显然,这与教师的教学行为有关,学生习惯于在题目要求画图时才画图,不要求画图就不画图。因而,教师更需加强对学生具体的画图方法的指导和实践,引导学生在运用画图策略解决具体问题的过程中,逐渐养成自发的画图习惯和意识。
三、 寻根究源,简约建构中提炼数学思想
著名数学教育家米山国藏说:“我们走向社会后, 能够留在我们脑海深处的是数学的思维、数学的方法以及数学的思想。”因而在数学教学中,教师要善于结合具体内容的教学渗透数学思想方法,使学生更好地理解和掌握相内容,更好地感受数学的精神和精髓,学会用数学的眼光看世界,学会数学地思维。而在实际教学中,教师仍习惯于就事论事,难以摆脱具体问题情境的束缚,缺乏以数学思想方法统领教学的基本理念。如在教学“间隔规律”时,许多教师往往只注重“找”规律,即出示情境图让学生先认识情境图中的一一间隔现象(夹子与手帕、兔子与蘑菇等),并让学生在表格中填写相关物品的个数,探究发现 “两端物体相同时,两端物体会比中间物体多1个”“两端物体不同时,两种物体一样多”的规律。
显然,这样的探究是肤浅的。教师未能从间隔规律中挖掘其蕴含的数学思想方法(一一对应思想),导致教学中的“看图说话”,规律探究未能发挥其应有的教学价值。特级教师周卫东在教学本课时,首先让学生观察两组图形的排列,在比较中感受并体会了什么是“一一间隔”现象;接着让学生“创造”一个“一一间隔”的排列,并开展“站队”游戏,让男生女生按性别“一一间隔”站好队;游戏过后,周老师对同学们提出了更高的要求,把不同的数据进行整理、分类,从而体会“一一间隔”的两种情况:一一对应,两种图形一样多;一一对应后还多出一个。这样,通过挖掘间隔规律中的一一对应思想,让学生进行意义建构,获得对规律本质的深入而透彻的理解。
在小学数学教材中,蕴含数学思想的教学内容还有很多,如假设策略中的数学模型思想,平均数、中位数中所蕴含的统计思想,正反比例关系图像中的数形结合思想等。回到原点,以数学思想来统领数学教学活动的开展,可以促进学生对数学本质的理解,对数学知识进行简约构建,进而获得有利于自身全面发展的数学素养。
四、 原型再现,释疑解惑中感悟数学方法
在“公因数和公倍数”的课后练习中,有这样一道题:
小华的爸爸上5天班休息一天,妈妈上3天班休息一天。如果小华的爸爸、妈妈3月10日同时在家休息,那么下一次同时在家休息是几月几日?
学生在解答此题时,绝大多数学生能直接求出5和3的最小公倍数15,然后用3月10日加15天得到3月25日。显然,学生并没有真正理解题目的含义,而如果直接告诉学生“爸爸上5天班休息一天”就是“每6天休息一次”,学生还是会感到难以理解,即使接受教师的看法也只是“被动地接受”,并非真正地理解其中的数理关系。
那么,怎样让学生真正地理解“爸爸上5天班休息一天”的含义呢?笔者启发学生:你们知道 “爸爸上5天班休息一天”到底是什么意思吗?可以借助什么来帮助我们理解呢?学生说这个问题和日历有关,于是画出3月的日历,再在日历上把爸爸、妈妈休息的日子分别找出来,问题就迎刃而解了。(如图3)
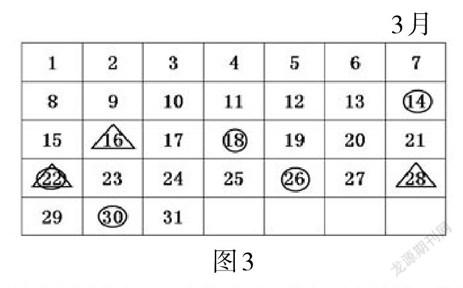
教师在学生面对复杂疑难问题纠结、茫然时,不妨退一退,回到问题情境的初始状态,这样学生就更容易清晰地认识问题的本来面目,获得最为原始但又最为深刻的认识和理解。当然,我们不能仅仅满足于解决问题,还应对问题解决的过程作进一步的思考:你现在理解了“爸爸上5天班休息一天” “妈妈上3天班休息一天”这两句话了吗?经过的天数还可以怎样求得呢?回到原点,同时在问题的思考中走向深刻,学生的数学学习能力得以提升,对数学方法的掌握也更为牢固。
【责任编辑:陈国庆】
