三正态分布—数量性状遗传理论新解

摘要

用与生产关系密切且广泛存在的孟德尔群体，讨论数量遗传理论。首先，对NilssonEhle小麦粒色实验的原始资料进行分析，得知小麦种皮的深红色受3对基因控制，进而作X²检验，说明数量性状受多基因控制。用Lyapunov中心极限定理证明，基因型值G呈正态分布，小生境环境效应E呈正态分布。从概率角度，阐述G与E的独立，用正态分布的可加性合成G与E，使P=G+E呈正态分布，并且绘制出三正态曲线图。这说明在随机交配下，不论是否连锁，不论基因效应是否相等，不论等位基因是否存在显性和什么样的显性，表现型值P均服从正态分布。吸收微效多基因假说的合理内核，引入环境效应，其应用范围突破微效多基因假说，更加全面和科学。

关键词 数量性状遗传;孟德尔群体;中心极限定理;基因型值G;环境效应E;表现型值P;正态分布

中图分类号 S188+.1;Q348  文献标识码 A  文章编号 0517-6611（2015）03-004-03

Three Normal Distributions—A New Solution for Theory on Quantitative Inheritance

ZHANG Tingzhen

（College of Forestry， Northwest A & F University， Yangling， Shaanxi  712100）

Abstract The theory on quantitative inheritance was discussed in Mendelian group which had a close relation with production. At first the original data of NilssonEhle wheat experiment was analyzed with known genetic knowledge. It was found that red color in the seed coat of a very old red variety was determined by three independent allelomorphic pairs and then a X² test was made indicating quantitative characters were determined by multiple genes. By means of Lyapunov central limit theorem it was certificated that both genotypic value G and the environmental effect in a niche E would be subordinated to the normal distribution and respectively. The independence between G and E was illustrated in the light of probability theory. According to the additivity of independent normal distribution P was composed of G and E making the phenotype value P=G +E would be submitted to the normal distribution N （μG+μE， σ²G+σ²E ）， whether or not the linkage was present， whether or not every gene effect was equal， whether or not there was dominance and what kind of dominance between alleles.

Key words  Inheritance of quantitative character; Mendelian population; Central limit theorem;

Genotypic value G; Environmental effect E; Phenotypic value P; Normal distribution

作者簡介

张廷桢（1939-），男，陕西户县人，教授，从事林木遗传育种方面的研究。

收稿日期 20141205

数量性状遗传是遗传学的重要内容之一。自1909年NilssonEhle发表小麦杂交实验100年以来，国内外在数量遗传理论上都延用着他的研究，但许多人将F₂（种子）的表现型隐去真像，指出由白粒到深红粒有多种级别。实际上，小麦F₂胚外包被的是母体F₁₂n组织，种子应是同一红色。这里所谈的是一种假象。这是其一。第二，没有引入组成数量遗传的另一重要组分——环境效应。NilssonEhle认为没有环境影响。Ayala等认为，环境对小麦粒色变异的影响极小。在NilssonEhle实验中，环境的影响可忽略不计。确切地说，他研究的是数量性状遗传的基因型部分，就基因的积加作用来说，只是比两对基因的遗传多了一对，不能产生数量性状遗传的完整理论。第三，现行的多基因假说设立很多不切实际的禁区，如要求无连锁、各基因效应相等、等位基因只能是不完全显性或无显性等，难以解释自然界生物普遍存在的数量性状遗传的许多问题。沈德绪等认为，数量遗传涉及的是群体内不同个体上同一性状的差异，应在群体水平上进行研究。笔者以与生产关系密切且广泛存在的孟德尔群体为对象，提出数量性状遗传理论新的研究方法和途径，取得满意结果。

1   数量性状受多基因控制

NilssonEhle以小麦为材料，第一个以多基因假说解释数量性状的遗传。该假说以基因效应相等为前提。后来的研究表明，同一基因位点和不同基因位点基因效应不一定相等。下文并不违背这种观点。

小麦种子胚外包被的是母体2n组织，其表现型由母体基因型决定。从母体所结种子颜色（下代粒色）及其分离状况可推断出母体的遗传组成。

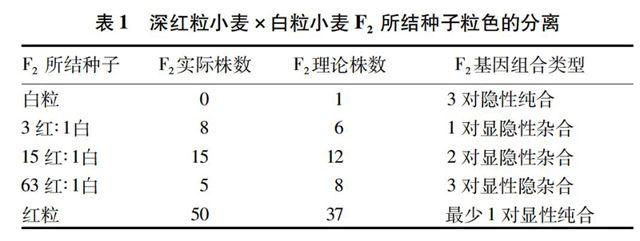
1900年NilssonEhle在位于Svalto 的“Sveriges Utsadesforening”植物育种站的调查发现，瑞典北部有一种种皮深红的小麦。用它与白粒品种杂交，F₁和F₂分别自交，结果78株F₂中，由于试验株数少，没发现一株所结种子全为白粒;而8株所结种子红粒和白粒分离为3∶1，15株所结种子红粒和白粒分离为15∶1，5株的分离为63∶1，50株全结红粒种子。种子颜色呈连续性变异^[1]。这是小麦的分离世代，其亲本性状白粒植株最低的频率为1/64，可以认为这一组合的亲本由3对独立基因控制。连续性变异是以性状的相似性为前提的。据已有的遗传知识，在2 至多对基因的遗传中，F₂代都有截然不同的性状。只有猪的毛色和南瓜果形等的遗传，当2种显性基因同时存在和二者之一存在时分别表现出相似的2种性状。这是猪的毛色和南瓜果形分别受2对独立基因控制，F₁₄种雌雄配子16种组合中显性基因积加作用的结果。若将相似性状合并，猪的毛色以棕色、南瓜果形以近球形讨论，则F₂的表现型比例为15∶1。容易推知，在该试验中红粒和白粒的63∶1分离是3对独立基因所产生的8种雌雄配子的64种组合的结果。在这里，基因的作用应该是积加的。对该推论可作进一步的检验。按已知3对独立基因控制作物遗传，以显性基因的积加作用来分析，F₂基因的组合类型如下：3对隐性基因纯合体，即没有一个显性基因的个体为C⁰₃=1;含1对显隐性基因杂合的个体为2C¹₃=6;含2对显隐性基因杂合的个体为4C²₃=12;3对显隐性基因杂合体为2³C³₃=8。同样分析，可以得出其他个体为37，它们由含1对显性基因纯合的个体起，显性基因递增、显性基因纯合与显隐性基因杂合共存的个体，到3对显性基因纯合体。这是F₂所结种子粒色分离的基础。这个结果与East所报道的是一致的。在64 株小麦F₂中，与NilssonEhle实验相应粒色分离比例种子的理论期望株数分别为1、6、12、8和37（表1）^[1]。

表1 深紅粒小麦×白粒小麦F₂所结种子粒色的分离

F₂所结种子F₂ 实际株数F₂ 理论株数F₂ 基因组合类型

白粒013对隐性纯合

3红∶1白861对显隐性杂合

15红∶1白15122对显隐性杂合

63红∶1白583对显性隐杂合

红粒5037最少1对显性纯合

X²=8.110<9.488（0.05，4）， 与期望值符合。可见，深红粒色小麦确实由3对独立基因控制。Melntosh进一步研究证明，自然界有15个3基因小麦品种。后来更多专家指出，许多生物的数量性状如高度、质量、奶牛的产奶量、肉牛的大小等受多基因控制，有的多达几十个基因含连锁基因。基因越多，各基因作用越小。正是群体中控制不同个体某一性状的多基因效应和小生境环境的多因子作用相结合，构成了独成体系的数量性状遗传。

2  基因型值G呈正态分布

基因型值是指基因型各位点从父母所获得控制某性状基因的效应之和，是从生命原始体胚和种子开始就具有的一种潜在能力。它赋予人类精子库和作物种子的经济价值。

数量性状遗传受多基因控制，以G表示孟德尔群体中具有某数量性状个体的基因型值，以Gi表示第i个基因位点对该值的贡献。由于上位不甚重要，可将其忽略，则

G=G₁+G₂+…+Gn

首先，上述数学模式表明各基因位点的贡献是可加的。其次，基因型值G是由不同位点贡献的， 每个基因位点的贡献较小。据Ayala 等进一步研究，同一基因位点和不同基因位点基因效应不一定相等。即使如此，甚至加上现代方兴未艾的转基因效应，上述数学模式仍成立^[2]。重要的是，在这里将研究限定在孟德尔群体。在随机交配下，不同位点的贡献Gi在遗传上是相互独立的，不论各位点是否连锁^[3]。因为具连锁基因的个体经多次随机交配，可形成一个随机交配的平衡群体。连锁基因的合子比例和独立基因的比例一样完全决定于基因频率。连锁基因决定的性状也是独立分布的^[4]。而显性、部分显性和超显性只作用于同一基因位点之间。当它们存在时，不同位点的贡献Gi也是独立的^[2]。此外，基因型值G在群体中又是随基因型及其频率不同而变化的随机变量。Lyapunov中心极限定理指出，自然界存在许多随机变量。它们受相互独立随机因素的综合影响，其中每个因素在总的影响中所起作用很小，则无论各因素引起的组分随机变量服从什么分布，当这种组分随机变量的项数充分大时，该随机变量就服从正态分布。按照Lyapunov中心极限定理，当基因位点数n充分大时，基因型值G服从正态分布N（μG，σG²）。

3   小生境环境效应E近似地服从正态分布

小生境环境效应也叫环境离差，用E表示。它是对数量性状作贡献的另一组分。

生物生长在一定环境中。环境效应是由许多因素综合作用的结果。这些因素包括光照、温度、水分、大气、营养物质、土壤、地貌、人为措施等。各种因素还可细分为许多小因子，如迄今已研究的植物所必需的营养元素达19种之多。每个生物都生活在由许多环境因子组成的小生境中。

就概率论来说，小生境中环境因子的作用，至少相当多因子的作用，可以认为在统计上是相互独立的。当测量、射击等应用中心极限定理计算误差时，对光、温度、大气及其湿度、人为因子等作用就是这样处理的^[5-7]。土壤及其他因子作用的独立性更是不言而喻的。许多数学家在说明生物的数量性状呈正态分布，如中国男性体高以1.69 m为众数、女性以1.62 m为众数的正态分布，虽忽视或低估了基因型值这一大块组分，而对这些环境因子的作用均是潜在地以相互独立处理的^[2]。每一小生境环境因子贡献总和，即小生境环境效应，就是这许多相互独立的小因子作用的结果。

环境因子对环境效应的作用实际正是这样。如，1900年Liebig就植物的生长受任一最小量状态的营养物质限制，提出“限制因子定律”。1905年Blackman认为，任何一个生态因子不足，都可成为影响植物生长的限制因子，被称作“限制因子定律”。这说明各生态因子都重要，对环境效应起着不可或缺的独立作用，但每个因子又不起压倒一切的作用。这就满足了应用中心极限定理研究环境效应的必要条件^[2]。

孟德尔群体的先决条件之一是随机交配，而且有着一定的地域特点，就是在同一地域的同一物种也可有几个孟德尔群体。如一定面积的实生纯林、大型鸡场的鸡群、水库中的鱼群都可被认为是孟德尔群体。随机交配，再加上微效多基因作用，使得产生的差异较小的不同基因型随机地被分布在孟德尔群体所占据的环境场各小生境上，环境变异也就随机化。这样在影响不同基因型的环境因子之间没有系统误差^[2]。 容易看出，这些环境变异是来自非人为的一定自然条件下的小规模变动，从而不同基因型所享用的小生境环境效应是独立的随机变量^[3]。

其实，在自然条件下，即使有竞争，孟德尔群体所占据的环境场也会处于平衡密度或环境容载量（Carrying capacity）。个体保持一定密度，各个体有着自己的小生境，其环境因子满足着个体的要求和需要。小生境环境效应仍然是相互独立的随机变量。

根据Lyapunov中心极限定理，当相互独立环境因子作用个数n充分大时，受诸多环境因子综合影响的随机变量小生境环境效应E服从正态分布N（μE，σE²）。

4   P=G+E呈正态分布

P=G+E是通用的遗传模式。概律论认为，在P=G+E中，随变量G=（X≤x）与E=（Y≤y）的独立性，是指G与E中任一随机变量的取值对另一随机变量的取值没有什么影响，用数学式

P（G·E）=P（G）P（E）来表示。在孟德尔群体中G=G₁+G₂+…+Gn，其值取决于基因位点数n及其贡献Gi。群体中基因型值本质上像三大定律一样，由基因分离、重组形成配子，再结合为合子的遗传过程完成，与E无关;而环境效应E取决于光、温度、水分、营养物质及土壤诸因子的作用，与G无关，G与E独立^[2]。

在实践中，独立性常根据实际意义来判断。G与E之间没有关联或关联很弱，那就认为它们之间是相互独立的。Falconer認为，基因型和环境之间的关系交互作用方差只能在相当人为的状况下才能予以分离和衡量。由于微效多基因的作用和随机交配，孟德尔群体中个体的基因型是一个差异较小而随机分布的有序系列，基因型值G是随基因型及其频率变化而变化的随机变量;而群体所占据的环境又是自然环境，不是按各自特有的环境个体不能类集的“特殊环境”，E的分布并非决定于基因型。而且，孟德尔群体的地域性使得各基因型所处的小生境环境性质还不止是数理统计中所谓的“处理”的性质，因为一个孟德尔群体一般在环境上不大会遇到像不同的处理所提供的那样大的范围。从而，基因型值和环境效应的关联和交互作用很弱，可予以忽略，二者相互独立[2，3，8]。

通过上述讨论，笔者认为，在孟德尔群体中决定数量性状遗传的基因型值G呈正态分布N（μG，σG²），小生境环境效应E呈正态分布N（μE，σE²）。

因为                                           P=G+E，且G、E独立，

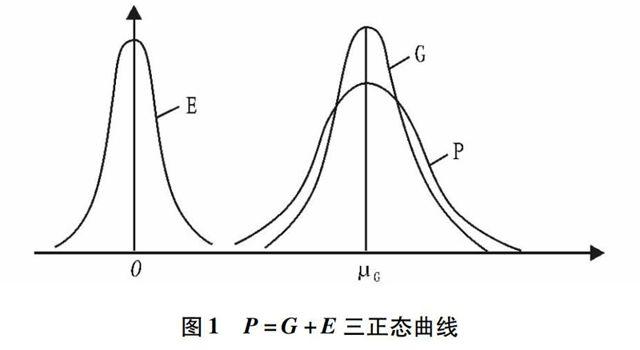
根据相互独立正态发布的可加性，  P=G+E～N（μG+μE，σG²+σE²）

由于P=G+E，E=P-G ，像测量误差的补偿性一样，在作为一个整体看待的群体里的平均环境离差取作0，即孟德尔群体的环境效应期望值μE=0 ，则

E～N（μE，σE²）=N（0，σE²）

P=G+E～N（μG，σG²+σE²）

这种关系的图示见图1。

图1 P=G+E三正态曲线

这说明在随机交配下，不论是否连锁，不论同一基因位点或不同基因位点基因效应是否相等，不论等位基因是否存在显性和什么样的显性，孟德尔群体数量性状的表现型值P均服从正态分布。这样，它吸收微效多基因假说的合理内核，引入环境效应，其应用范围突破微效多基因假设，而且更加全面和科学^[2]。由于各孟德尔群体相互独立，根据相互独立正态分布的可加性，就几个孟德尔群体，甚至就一个种来说，数量性状仍呈正态分布，自然界生物数量性状呈正态分布就相当普遍。

参考文献

[1]

NILSSONEHLE H.Kreuzungsuntersuchungen an Hafer und Weizen[J].Zeitschriftfür Induktive Abstammungsund Vererbungslehre，1910，3（1）：290-291.

[2] 贾小明，张廷桢，张焕玲，等.孟德尔群体数量性状遗传的概率论分析[J].西北林学院学报，2014，29（5）：106-110.

[3] BULMER M G.The Mathematical Theory of Quantitative Genetics[M].Oxford： Glarendon Press，1980：1-128.

[4] LI C C.群體遗传学[M].吴仲贤，译.北京：农业出版社，1981：6-394.

[5] 胡细宝，孙洪祥，王丽霞.概率论数理统计随机过程[M].北京：北京邮电大学出版社，2004：188-203.

[6] 林少宫.基础概率与数理统计[M].北京：人民教育出版社，1978：12-130.

[7] 叶鹰，李萍，刘小茂.概率论与数理统计[M].武汉： 华中理工大学出版社，2000：158-161.

[8] FALCONER D S.Introduction to Quantitative Genetics[M].2nd ed.Lond & Yort： Longman Group Ltd，1981：1-133.