弹簧问题分析要点例谈

张红珍

弹簧问题是高考的重点和难点问题，在长期的教学实践中摸索发现，解决弹簧问题主要有下面几种方法。

一、解决弹簧类问题的步骤多从初始状态入手，对物体进行受力分析（注意弹簧可能处于拉伸或压缩状态产生拉力或压力），过程分析，一般以力、运动、功、能的顺序分析

例1.如图1，质量为m1的物体A经一轻质弹簧与下方地面上质量为m2的物体B相连，弹簧的劲度系数为k，A、B都处于静止状态。一条不可伸长的轻绳绕过轻滑轮，一端连物体A，另一端连一轻挂钩。开始时各段绳都处于伸直状态，A上方的一段绳沿竖直方向。现在挂钩上挂一质量为m3的物体C并从静止状态释放，已知它恰好能使B离开地面但不继续上升。若将C换成另一个质量为（m1+m2）的物体D，仍从上述初始位置由静止状态释放，则这次B离地时D的速度的大小是多少？（已知重力加速度为g）。

解：开始时，A、B静止，设弹簧的压缩量为x1，有kx1=m1g ①

挂C并释放后，C向下运动，A向上运动，设B刚要离地时弹簧伸长量为x2，有kx2=m2g ②

B不再上升，表示此时A和C的速度为零，C已降到其最低点。由机械能守恒，与初始状态相比，弹簧的弹性势能的增加量为ΔE=m3g（x1+x2）-m1g（x1+x2） ③

由①②⑤解得B离地时D的速度的大小v=

二、在对物体进行受力分析的基础上，结合物体运动情况，分析物体分离的临界状态（一般为加速度相等、速度相等等）

例2.一个弹簧秤放在水平地面上，Q为与弹簧上端连在一起的秤盘，P为一重物，已知P的质量m1=10.5 kg，Q的质量m2=1.5 kg，弹簧的质量不计，劲度系数k=800 N/m，系统处于静止，如图2所示，现给P施加一个方向竖直向上的力F，使它從静止开始向上做匀加速运动，已知在前面0.2 s时间内，F为变力，0.2 s以后，F为恒力。求力F的最大值和最小值。（g=10m/s2）

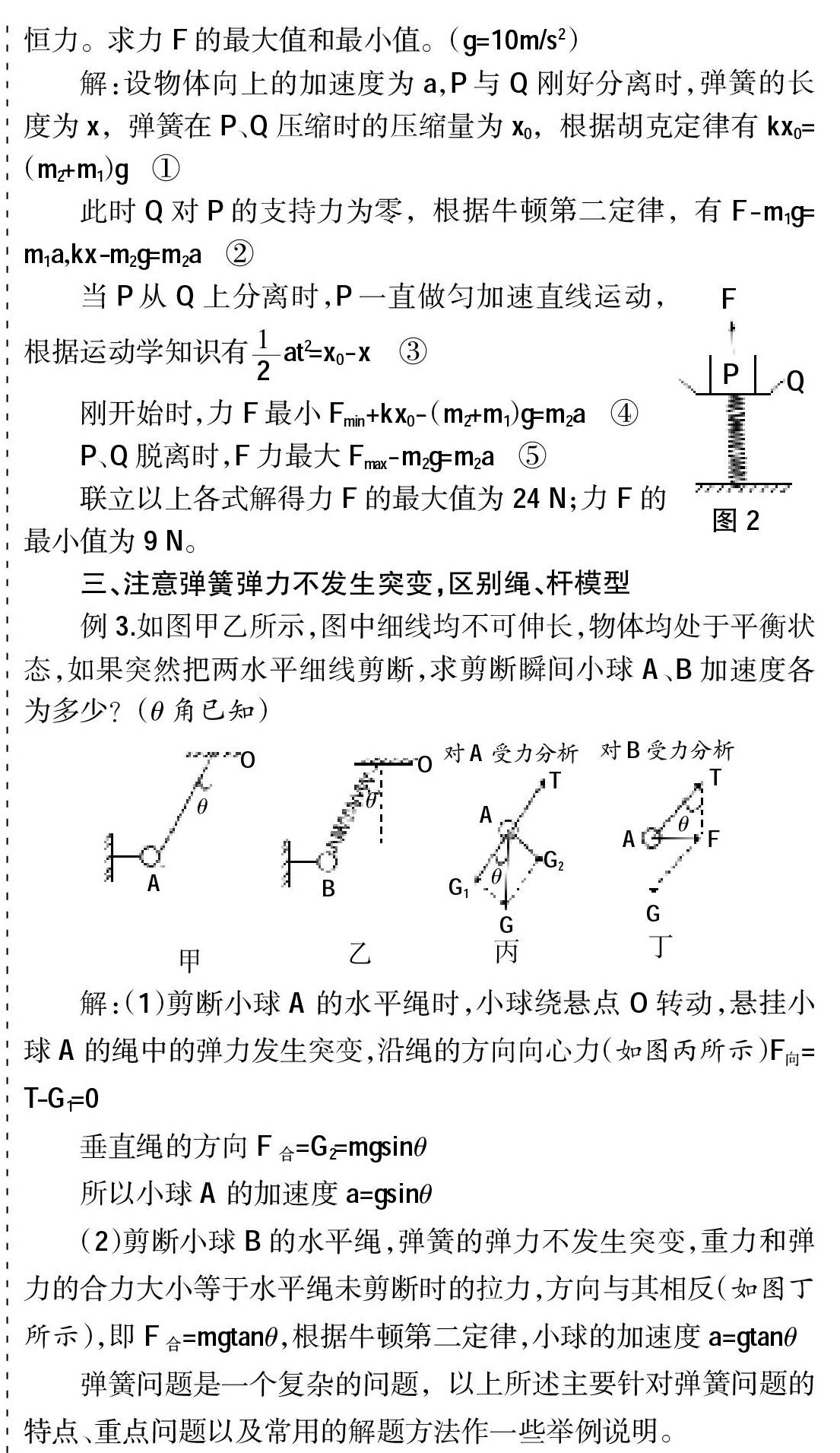
解：设物体向上的加速度为a，P与Q刚好分离时，弹簧的长度为x，弹簧在P、Q压缩时的压缩量为x0，根据胡克定律有kx0=（m2+m1）g ①

此时Q对P的支持力为零，根据牛顿第二定律，有F-m1g=m1a，kx-m2g=m2a ②

当P从Q上分离时，P一直做匀加速直线运动，根据运动学知识有at2=x0-x ③

刚开始时，力F最小Fmin+kx0-（m2+m1）g=m2a ④

P、Q脱离时，F力最大Fmax-m2g=m2a ⑤

联立以上各式解得力F的最大值为24 N；力F的最小值为9 N。

三、注意弹簧弹力不发生突变，区别绳、杆模型

例3.如图甲乙所示，图中细线均不可伸长，物体均处于平衡状态，如果突然把两水平细线剪断，求剪断瞬间小球A、B加速度各为多少？（θ角已知）

解：（1）剪断小球A的水平绳时，小球绕悬点O转动，悬挂小球A的绳中的弹力发生突变，沿绳的方向向心力（如图丙所示）F向=T-G1=0

（2）剪断小球B的水平绳，弹簧的弹力不发生突变，重力和弹力的合力大小等于水平绳未剪断时的拉力，方向与其相反（如图丁所示），即F合=mgtan？兹，根据牛顿第二定律，小球的加速度a=gtan？兹

弹簧问题是一个复杂的问题，以上所述主要针对弹簧问题的特点、重点问题以及常用的解题方法作一些举例说明。

编辑 温雪莲