“真伪探究”的碰撞
2015-10-21夏维
夏维
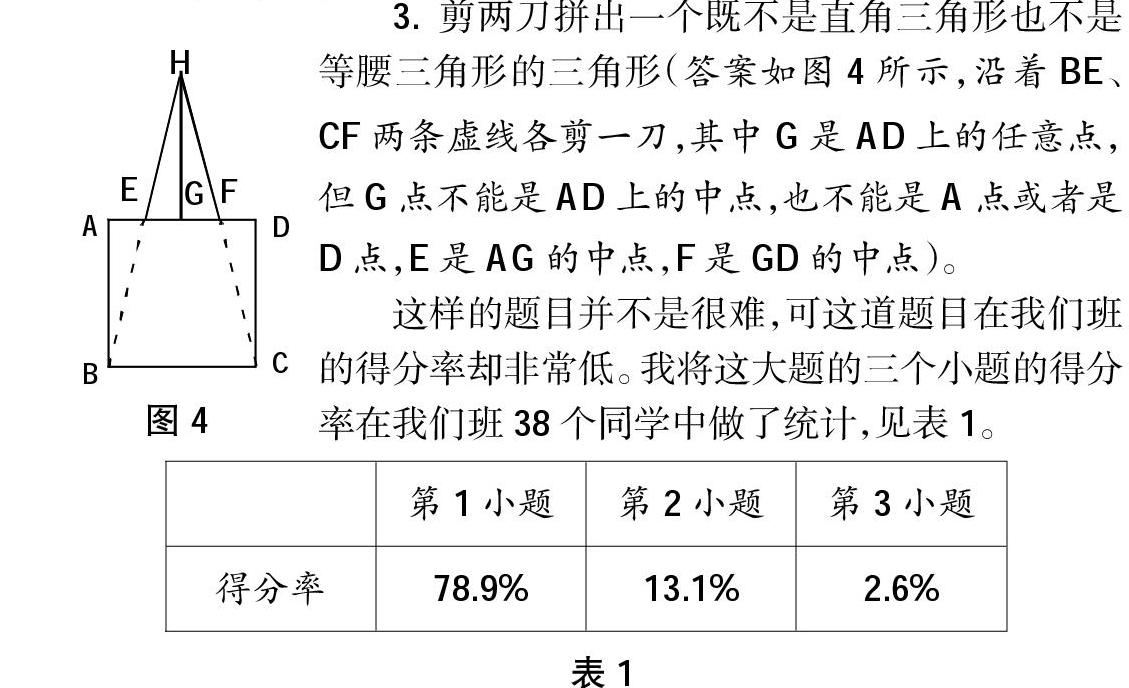
初三的教学考纲上有这样一道题目,有一个正方形ABCD,如图1所示,请你完成以下习题。
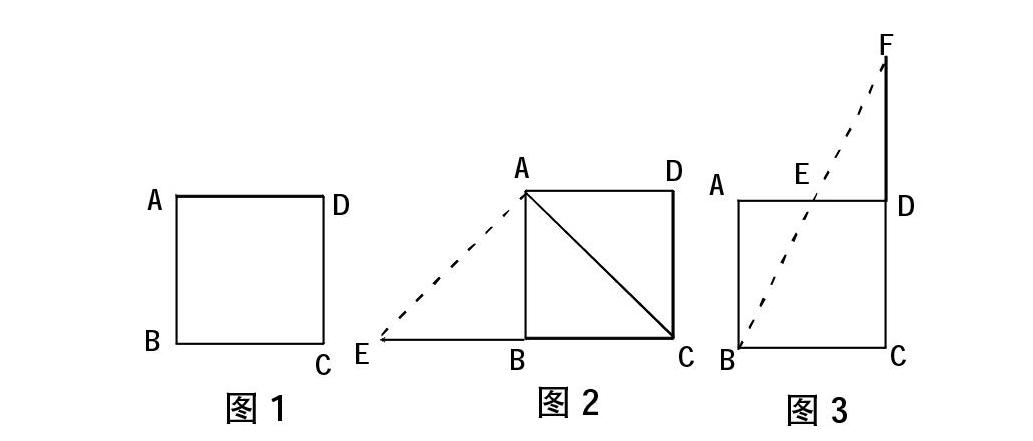
1.剪一刀拼出一个直角三角形(答案有两种,沿虚线剪一刀见图2、图3,图3中E是AD的中点);
2.剪两刀拼出一个不是直角三角形的等腰三角形(答案如图4所示,沿着BE、CF两条虚线各剪一刀,其中G是AD的中点,E是AG的中点,F是GD的中点);
3.剪两刀拼出一个既不是直角三角形也不是等腰三角形的三角形(答案如图4所示,沿着BE、CF两条虚线各剪一刀,其中G是AD上的任意点,但G点不能是AD上的中点,也不能是A点或者是D点,E是AG的中点,F是GD的中点)。
这样的题目并不是很难,可这道题目在我们班的得分率却非常低。我将这大题的三个小题的得分率在我们班38个同学中做了统计,见表1。
第三小题只有一个同学做出来,而且这位同学平时的数学成绩也是中等偏下的,然而,对于基础好的同学,会解很复杂的压轴题,对于这道难度一般的思维题却束手无策了。这样的现象引起了我的深思,甚至恐慌。我的学生给定条件去求解或证明是非常棒的,但是遇到操作题、开放题却束手无策。他们好像是一台机器,设置好程序,他们会按部就班地去操作,但是如果遇到一些比较新颖的,平时没见过的,他们就很难解决了。这就给我们在实际教学中更好地开展探究性教学提出了更高的要求。
一、认识“伪探究”
《义务教育数学课程标准》指出:数学教学活动是师生积极参与、交往互动、共同发展的过程,是学生学与教师教的统一。作为21世纪的新型教师,我觉得我们不会像以前的老师一样进行“满堂灌”的教学。我们自认为平时都让学生在观察、猜测、探究,但是我们有没有进一步思考过,我们的探究是真正的探究吗?
我们以三角形的全等判定第一课“边边边”为例进行分析,部分教学片断如下:
师:三边对应相等的三角形是否全等?
(同学都认同,老师提出的问题肯定是对的,就是今天要学习的内容,这样就相当于给学生的思维确定了范围,学生只能按照老师说的去思考。)
师:现在给你们三条边,让我们一起来做个实验,请大家先画一个三条边分别是3 cm、4 cm、5 cm,书本上有三角形的画法,大家可以参考一下。
(学生生开始认真地画三角形。)
师:接下来请把你们画的三角形用剪刀剪下来,同桌之间、前后桌之间比一比,相互交流一下,看看是不是一样的?
生:比较之后,都说是一样的。
师:好的,那么下面请同学们看多媒体演示,两根木棒的一端由螺栓固定在一起,木条可以自由转动,在转动过程中,连接另两个端点所成的三角形的形状、大小随之变化。如果把另两个端点也用螺栓固定在第三根木条上,那么构成三角形的形状大小就完全确定。从以上两个活动中我们可以得出什么结论?
生:三条边相等的三角形全等(异口同声)。
整个教学过程,有画图、有观察、有讨论、有猜测,完全是一番探究的模样。但是我们再仔细想一想为什么要让学生探究,探究的目的是培养学生研究新事物的能力,培养学生的创新思维。那么,什么是创新思维?创新思维是指对事物间的联系进行前所未有的思考,从而创造出新事物的思维方法,是一切具有崭新内容的思维形式的总和。然而像本课这样的探究,是教师预设的、既定的,即我们已经为学生设计好了多个步骤,只要学生单纯模拟,去按照老师的方法去做就行,学生往往不知道为什么要这样做,而学生也深信老师提出的肯定是正确的结论,只是根据老师给出的验证方法,再验证一遍正确结论而已。学生就像困在笼子里的小鸟,不能展翅高飞。这样的教学探究,实际上是一种“伪探究”。
二、学习“真探究”
同样,让我们从三角形的全等判定第一课“边边边”的另一篇教学案例说起:
师:我们已经学习了全等三角形的概念和性质,请同学们回忆全等三角形有哪些性质?
生:全等三角形的对应边相等,对应角相等。
师:用几何语言如何表示?
生:∵△ABC≌△DEF
∴ AB=DE,AC=DF,BC=EF,∠A=∠D,∠B=∠E,∠C=∠F。
师:要判定两个三角形全等需要几个条件呢?
生:(迅速地)需要六个条件,三条边和三个角都对应相等。
师:(微笑地肯定)如果三条边和三个角都对应相等,确实能判定两个三角形全等,但是否必须满足六个条件才能判定两个三角形全等呢?接下来请同学们交流一下,看看要多少个条件?
交流后学生汇报结果:
师:一个条件可以证明吗?
生:一个条件肯定是不够的,比如一个角相等或者一条边相等是不够的,我可以通过画图来举反例。
师:两个条件够吗,两个条件有几种情况呢?
生:……
师:三个条件呢?有哪几种情况?
生:……(有些条件直接被学生否定掉了,剩下了其中几个条件还不确定)
师:你们真厉害,一下子就排除了那么多,还有几个条件我们还不确定能不能证明,那么,今天就先让我们来研究一下三边对应相等的三角形是不是全等,你们想怎么研究?
生:讨论后汇报
……
教育家波利亚说过:“学习任何知识的最佳途径是自己去发现”。本节课从设置情景提出问题,到动手操作、交流,直至归纳得出结论,整节课中学生参与教学活动、积极思维、创造性地解决问题,学生的主体作用得到了较好的体现,整个过程学生不仅得到了两个三角形全等的条件,更重要的是经历了知识的形成过程,体会了一种分析问题的方法。而在整个课堂教学中想怎么研究,想怎么做,一切都让学生思考,教师始终扮演引导者和组织者的角色。我想这才是真正的探究式教学。
三、走出“伪探究”
为了能够走出“伪探究”教学,我觉得我们可以从以下两个方面入手:
1.从学生方面入手,让学生打破思维定势,思维定势来自对权威的认同或是从众心理等方面。比如,我曾经在读者中看到过这样一篇文章,一位法国教育心理学家曾给学生出了这样一道题目,说在一条船上有86头牛,有34只羊,问船长的年龄有多大。好多学生给出的答案是86减34得到的52,但牛羊的数量和船长的年龄并没有必然的關系。这就使学生陷入认同权威的思维定势的陷阱,学生相信既然是教育学家出的题就一定是有解的,他们就不顾真实的联系给出一个答案。那么,在教学过程中,教师作为权威形象的代言,就要鼓励学生提出自己的观点和看法,鼓励学生独立思考,向教师的看法提出挑战,培养学生“不唯书,不唯上,只唯实”的学习态度,即培养学生以真理为准的学习态度。
2.从教师方面入手,让教师明白教师不是课堂的“主宰”,教师是学生学习动机的激发者和课堂气氛的营造者,教师是课堂行为和学习效果的评价者。素质教育中要求教师在教学中要改变自己已经习惯了的教学方式,有意识地给学生创造机会,让他们亲身体验学习探究的全过程,真正使学生获得全方位的发展。让我们教师把课堂还给学生,多一点“真探究”,少一点“伪探究”,让我们的孩子走出“笼子”,飞向蓝天!
参考文献:
李德果.初中数学探究性教学的探索[J].读与写:教育教学刊,2008(10).
编辑 段丽君