基于相关与回归分析的城市出租车情况研究
2015-10-21霍俊爽朱翠娟张若东邰志艳孙庆峰王柳行
霍俊爽 朱翠娟 张若东 邰志艳 孙庆峰 王柳行

1、引言
近年来伴随着城市的发展,人口和车辆的增多,使得人们经常遇到打车难等问题。城市怎样合理的配置出租车的数量,直接关系到城市居民的生活质量,基于以上原因,本文将从出租车的里程利用率、车辆满载率、万人拥有量、地区面积、地区人口、地区人均GDP以及价格等因素分析城市配置出租车的数量等情况。
2、基本理论
2.1里程利用率
定义1:里程利用率公式为:,其中L为里程利用率,S营为营业里程,S行是行车里程。里程利用率是衡量出租车供求状况的主要指标,规定标准为出租车利用率为52%,达到供求平衡状态。里程利用率高说明载客量高,反之,则载客量低。
2.2车辆满载率
定义2:车辆满载率是通过对不同时间同一位置载客车数与总通过车数的比值来确定。车辆满载率计算公式为:,其中M为车辆满载率,Z为载客车辆数,T为总通过车辆数。利用车辆满载率可以分析不同时空出租车资源的“供求匹配”程度,一般车辆满载率应达到70%,才能使供求配比相对合适。
2.3万人拥有量
定义3:万人拥有量的计算公式为Y=C/R,其中Y表示万人拥有量,C表示出租车拥有量,R表示总人口数,以万为单位。万人拥有量是出租车供应量的重要指标,按照规定大城市中出租车万人拥有量的标准是20辆/万人。
2.4相关系数理论
定义4:相关系数又称为Pearson积差相关系数,是用来说明具有直线关系的两变量间相关的密切程度与相关方向的指标,其计算公式为:
其中r表示样本相关系数,其没有单位,其值为-1≤r≤1。
2.5多元回歸分析理论
定义5:研究因变量(被解释变量)与两个或两个以上自变量(解释变量)之间的回归问题,称为多元回归分析。多元线性回归方程可写为:,其中X1,X2,...XK为自变量,b0为常数项,b1,b2,...bk为待定的偏回归系数,为在自变量X1,X2,...XK时因变量的总体平均值的估计值。
3、实证分析
3.1北京市出租车里程利用率
由里程利用率公式求得北京市2015年1月到7月出租车的里程利用率和车辆的空驶率,见表1。
从表1可以看出北京在1-7月的时间段内,出租车的里程利用率均大于52%,从而说明北京市的出租车的供求匹配不均衡。
3.2北京市某地不同时间出租车满载率
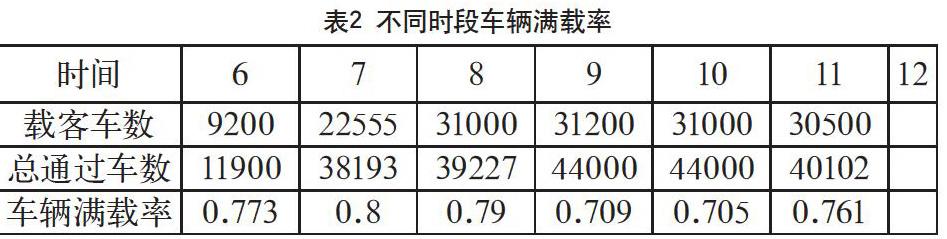
为了研究不同时间对车辆满载率的影响,统计了同一点某一天中不同时间段的载客车数与总通过车数,并用车辆满载率公式计算出来车辆满载率,见表2.
3.3北京市出租车万人拥有量
北京市人口约1136万,出租车数约61740辆,万人拥有量约为54.3辆/万人。
3.4车辆满载率相关性分析
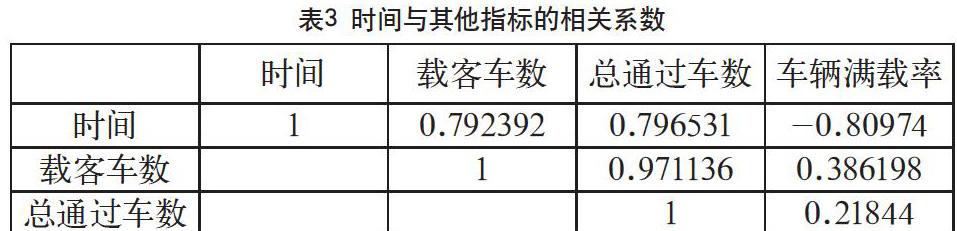
基于R软件、MATLAB软件、SPSS软件等计算了时间与载客车数、时间与通过车辆数、时间与车辆满载率的相关性,见表3。
从表3不难看出载客车数与总通过车数的相关系为0.971136,高度相关,并且时间与车辆满载率的相关系数也比较大。说明时间与车辆满载率的相关性也比较强。
3.5出租车数量的多元回归分析
根据我国北京、长春、哈尔滨、南京、杭州、福州、合肥、郑州、武汉、长沙、成都、西安等主要城市的地区面积X1(km)、地区人口X2(万人)、人均GDPX3(万元)、价格X4(元/5km)、出租车数量(辆)等数据对城市出租车数量进行回归分析,得到如下回归方程:
其中Y是出租车数量。由此回归方程进行预测出租车数量增长时,算得供求关系平衡下的出租车的空车率约32%。
(作者单位:1.吉林医药学院公共卫生学院;2.北华大学汽车与建筑学院)
作者简介
霍俊爽(1982-),男,硕士,讲师,研究方向:应用数学与统计学。
△通信作者:王柳行(1965-),男,教授,硕导,吉林医药学院教务处处长,研究方向:社会医学、教育管理.
