泰州城南作业区码头工程对航道条件影响分析

摘要： 泰州城南作业区码头工程位于北澄子河与南官河交汇处，水流条件十分复杂，因此在此建设码头需要通过对航道条件影响分析的详细论证，才能进行建设。本文通过实测数据，建立平面二维水流数学模型进行系统的分析，并得到相关研究结论。本文研究成果可为类似工程提供参考

关键词： 航道条件；数学模型；水流紊动；流场分析

1 工程概况

泰州内河港兴化港区城南作业区码头工程位于盐邵线航道上南官河西岸和北澄子河北岸交汇处。北澄子河在泰州市境内起点为南柯东，终点为河口，航道里程 43.73 公里。在工程区域内水面宽65～85m，主航道与码头前沿高程在-4.22～-2.54m的范围内，设计低水位下航深在3.20～4.88m范围内。航道等级现状为三级。南官河在泰州市境内起点为古殿堡，终点为汤庄，航道里程46.27 公里。在工程区域内水面宽80～110m，主航道与码头前沿高程在-6.80～-2.54m的范围内，设计低水位下航深在3.20～7.46m范围内。航道等级现状为三级。

2 数学模型建立

2.1 研究范围

模型北澄子河上边界位于两河交汇处上游约980m，模型南官河上边界位于两河交汇处上游约820m，模型下边界位于两河交汇处下游约200m。模型范围见图1。

2.2 计算工况

根据兴化市航道局、兴化市水务局、兴化市水文局提供的相关资料，选取最不利计算情况，即最高通航水位，将计算工况列于表1。

3 计算结果分析

将最高通航水位工况下，码头建成前后的流场图绘于图2，码头建设后流场绘于图3。对比码头建成后工程河段流场大小变化。

分析上图可知，码头建设前最高通航水位下，工程河段流速范围为0.08～1.96m/s，过水区域（尤其是北澄子河）较窄，北澄子河与南官河水流在交汇处对冲，形成复杂流场，影响周围水域，局部区域有环流出现，对冲区域流速范围在0.08～0.42m/s，流速大小明显降低，流场线方向较为杂乱。码头建设前最高通航水位下，由于岸线向陆域开挖，以及码头前沿的大范围数据，过水区域面积显著增大（尤其是北澄子河），工程河段流速范围在0.05～1.72m/s，流速大小较码头建设前显著下降。同时，码头建设后，两河交汇对冲角有一定程度减小，对冲区域流场趋于平顺。码头建设后，整个工程河段流速变化范围在-0.95～0.33m/s范围内，绝大部分区域流速显著下降，两河主流对冲角由114°下降至105°，造成的流场紊动有一定程度的改善，流场线趋于归顺。

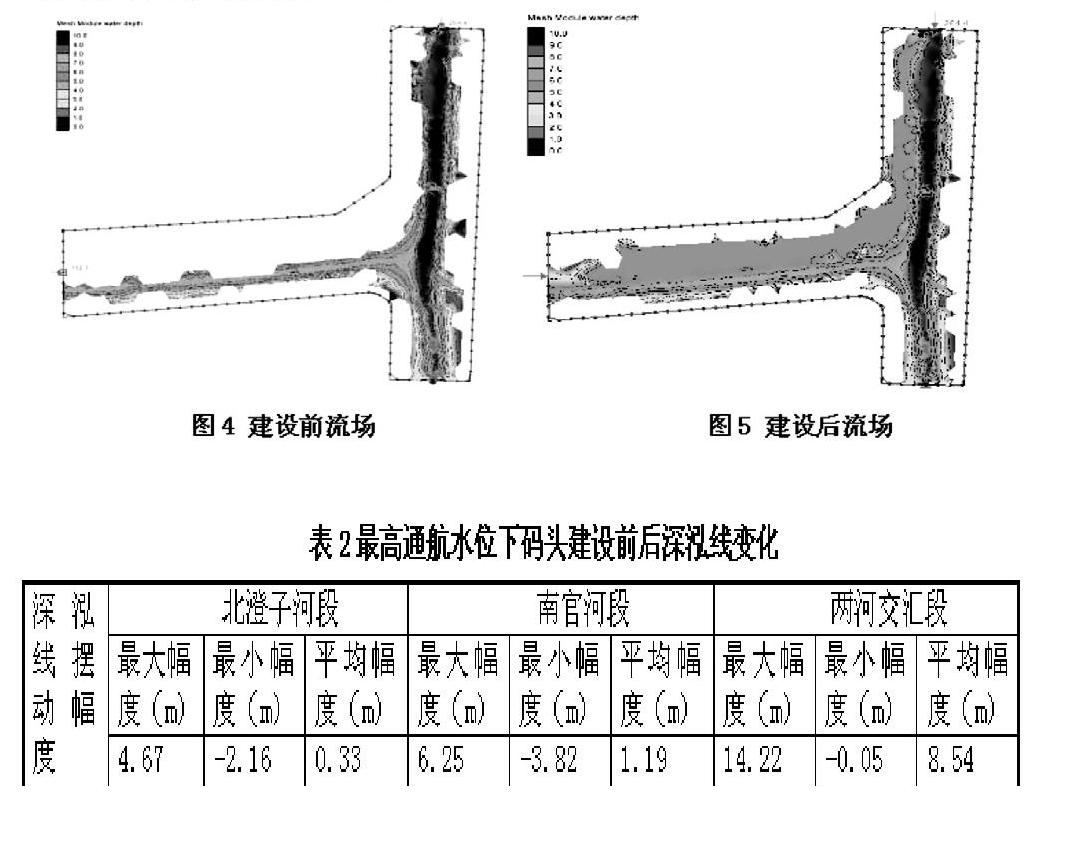
将最高通航水位工况下，码头建成前后的水深图绘于图4，码头建设后水深绘于图5。

分析图4至图5可知，码头建成后，工程河段过水面积增加。在码头前沿，由于人工疏浚，河床高程大幅下降，水深增大。而在主航道区域，码头建设前后水深变幅在-0.2～0.18m范围内，基本不影响航深。

同时，由于主航道航深变化很小，因此码头建设后航道区域满足通航要求的区域不变，航宽也不会减小。

码头建设后，深泓线主要在两河交汇处出现小幅向凹岸摆动，导致这一现象的原因是因为两河交汇处水流对冲，引起紊流，在凸岸河段有一定程度的泥沙淤积，在其他区域则摆动幅度较小（表2）。

4 结语

本文通过建立平面水流二维数学模型，分析了泰州內河港兴化港区城南作业区码头工程建设后对航道条件的影响，从分析结果来看，该码头建成后，航深、航宽基本不变，深泓线摆动较小，绝大部分区域流速显著下降，两河主流对冲角由114°下降至105°，对冲造成的流场紊动有一定程度的改善，流场线趋于归顺。可见码头建设后对航道条件基本上没有不利影响，该码头适合建设。本文研究结论可为同类工程提供参考与借鉴。

参考文献：

[1] M.A.Gill.Erosion of Sand Beds Around Spur dikes [J].Journal of the Hydraulics Division， ASCE， Vol 9， 1972.

[2] Koutitas Christopher G.Elements of computational hydraulics [M].New York：London Pentech Press， 1983.

[3] 长江水利水电科学研究院. 水库不平衡输沙的初步研究[A].水库泥沙报告汇编.黄河水库泥沙观测研究成果交流会文集[C].1973.

[4]陈 辉， 刘志雄， 江耀祖. 引航道通航水流条件数值模拟[J]. 水利水运工程学报， 2012.8（4）：13-18.

作者简介：金辉杰（1987- ），男，浙江东阳人，大学本科，助理工程师，主要从事水利水电工程设计。