不确定环境下投资收益与风险问题的模型研究

赵建华，李 薇，刘雅娜，曹志军

（石家庄学院 a.数学与信息科学学院；b.经济管理学院，河北 石家庄 050035）

不确定环境下投资收益与风险问题的模型研究

赵建华a，李 薇b，刘雅娜a，曹志军a

（石家庄学院 a.数学与信息科学学院；b.经济管理学院，河北 石家庄 050035）

描述了单位投资收益和单位投资风险是不确定变量时的投资问题.根据不同的决策准则，应用不确定理论建立了了两个新模型，即不确定期望值目标规划模型和不确定机会约束目标规划模型.为能简便快捷的求解模型，基于不确定理论的运算法则，将两种不确定模型转化为其清晰等价形式.最后通过1个数值例子说明了用不确定规划解决不确定投资问题的合理性与有效性.

投资问题；不确定理论；不确定变量；不确定规划；目标规划

0 引言

随着全球经济的迅猛发展，资本投资已成为当今最流行的盈利方式之一，许多公司都会利用自有资金进行投资，以期获得好的收益.但是由于投资市场的复杂性，资本投资既有收益又有风险.一般来说，期望的投资收益越大，风险也就越大.那么如何确定各种投资的比重，从而得到比较满意的投资收益，就成为决策者面临的主要问题.所以投资问题是研究如何把有限的资金合理分配到不同的投资项目中，从而达到提高投资收益并且降低风险的问题.

由于投资市场的瞬息万变，投资收益与风险系数具有诸多不确定因素.为有效处理这些不确定性问题，刘宝碇于2007年提出了新的理论——不确定性理论[1]，该理论建立在正规性、自对偶性、可列次可加性以及乘积测度公理的基础上，并形成了数学的1个分支[2].目前，这一理论经过不确定理论实验室（UTLAB）成员们的不断完善，在理论和实践方面取得了丰硕的成果[3-6].如今不确定理论已经扩展到很多领域，如不确定规划、不确定逻辑、不确定推理、不确定微积分、不确定统计等等.

笔者采用文献[7-9]所建立不确定规划，考虑单位收益、单位风险为不确定变量情况下，建立以提高收益、降低风险为目的不确定目标规划模型，即不确定环境下期望值目标规划模型和机会约束目标规划模型.为能方便快捷求解不确定规划模型，把不确定规划模型转化为其清晰等价形式.最后，给出了1个具体的例子，例子表明不确定规划可以有效解决不确定环境下的投资收益与风险问题.

1 预备知识

定义1 如果ξ是从不确定空间（Γ，L，M）到实数集R的可测函数，即对任意一个Borel集

是一个事件，则称ξ为（Γ，L，M）上的不确定变量.

定义2 设ξ是（Γ，L，M）上的不确定变量，若对∀x∈R满足Φ（x）=M{ξ∈B}，则称Φ是ξ的不确定分布.

定义3 设ξ是不确定变量，若其分布满足

则称ξ为“之”字形不确定变量，表为（a，b，c），这里a，b，c是实数，且a＜b＜c.如图1所示.

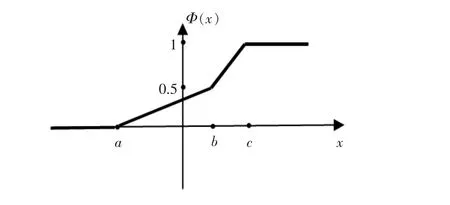
图1 "之"字形不确定分布

由定义3可得到具有之字形不确定分布的不确定变量ξ的逆分布为

定义4 设ξ1，ξ2，…，ξm是不确定变量，如果对任意的Borel集B1，B2，…，Bm满足

定义5 若ξ是不确定变量，Φ（x）是ξ的不确定分布，则称

为ξ的期望值，其中，两个积分中至少有1个是有限的.

定理1 设ξ为不确定变量，并且有不确定分布Φ和不确定逆分布Φ-1.如果ξ存在期望值，那么

特别的，如果ξ为“之”字形不确定变量，则

2 问题的描述

定理2 设ξi为相互独立的不确定变量，fi到R为R到R的函数，i=1，2，...，m.则 fi（ξi）也为相互独立的不确定变量，i=1，2，...，m.

定理3 假设相互独立的不确定变量ξ1，ξ2，…，ξn的不确定分布分别为Φ1，Φ2，…，Φn，若f（x1，x2，…，xn）关于x1，x2，…，xm是严格单增的并且关于xm+1，xm+2，…，xn是严格单减的，则ξ=f（ξ1，ξ2，…，ξn）的逆不确定分布为

考虑某公司对n个项目进行投资，为了建立投资规划模型，下列下标、决策变量和参数所表示的意义如下（资金单位为万元）：

i：投资项目的个数，i=1，2，..，n；

xi：项目i的投资量；

ξi：投资项目i的的单位收益；

ηi：投资项目i的单位风险损失；

ei：投资项目i的单位成本；

si：投资项目i的的单位交易费；

M：公司现有的总资金.

约束条件是总投资额加上总交易费不能超过公司现有总资金M，即：

由此建立确定环境下的投资收益与风险的多目标规划模型为

设ξi>si，否则不对该项目投资.

因此模型（5）表示在满足约束条件下，极大化公司的投资收益，并且极小化投资风险.

3 不确定规划模型

模型（6）是在确定条件下建立的，即模型中的参数都是固定的数.但由于投资环境的复杂性，导致许多数据不能精确量化，例如投资收益和投资风险往往不是确定数据，因此模型（6）只有理论意义，缺乏实用价值.为使投资问题更贴近实际情况，假设单位投资收益ξi与投资风险ηi是不确定变量.

将文献[7-9]中提出的不确定规划用于投资问题，根据不同的决策准则，建立相应的不确定目标规划模型.

假设决策者设定的投资总收益不小于目标值T0，总风险不超过目标值H0.并设总收益最大为第1优先级，为正负偏差变量，其优先因子为P1；总风险最小为第2优先级，为正负偏差变量，其优先因子为P2.

不确定期望模型的主要思想是最优化目标函数的期望值.笔者所指的期望值是在不确定测度意义的下不确定变量的平均值.

若ξi与ηi是不确定变量，由此可得下面不确定期望约束目标规划模型

不确定机会约束目标规划主要思想是在不确定环境下极大化不确定事件成立的机会，从而给出最优决策.笔者采用这种思想建立不确定投资问题的机会约束目标规划模型.

设α1，α2（α1>0，α2≤1）是决策者预先给定的置信水平，他们取决于决策者的主观性.显然置信水平越大，决策者的满意度越高，因此取α1，α2>0.5.由此建立如下不确定机会约束目标规划模型

4 清晰等价形式

模型（7）与（8）中含有不确定变量ξi与ηi，而笔者所建立的模型是线性模型，因此采用不确定变量的运算法则[1]推出模型（7）与（8）的清晰等价形式，从而更容易地求解不确定环境下投资收益与风险问题规划模型.

定理4 若ξi与ηi都是相互独立的不确定变量，其不确定分布分别为Φξi，Φηi，则模型（7）的清晰等价形式为

证明 由（3）式立即得到，证毕.

特别的，若ξi□（ai，bi，ci）与ηi□（pi，qi，ri）都是“之”字形不确定变量，根据（4）式，模型（7）的清晰等价式为：

定理5若ξi与ηi都是相互独立的不确定变量，其不确定分布Φξi，Φηi分别为，则模型（8）的清晰等价形式为

证明 利用不确定逆分布（5）式可得

且

证毕.

特别的，若ξi□（ai，bi，ci）与ηi□（pi，qi，ri）都是“之”字形不确定变量，则由（2）式可得模型（11）的清晰等价式为

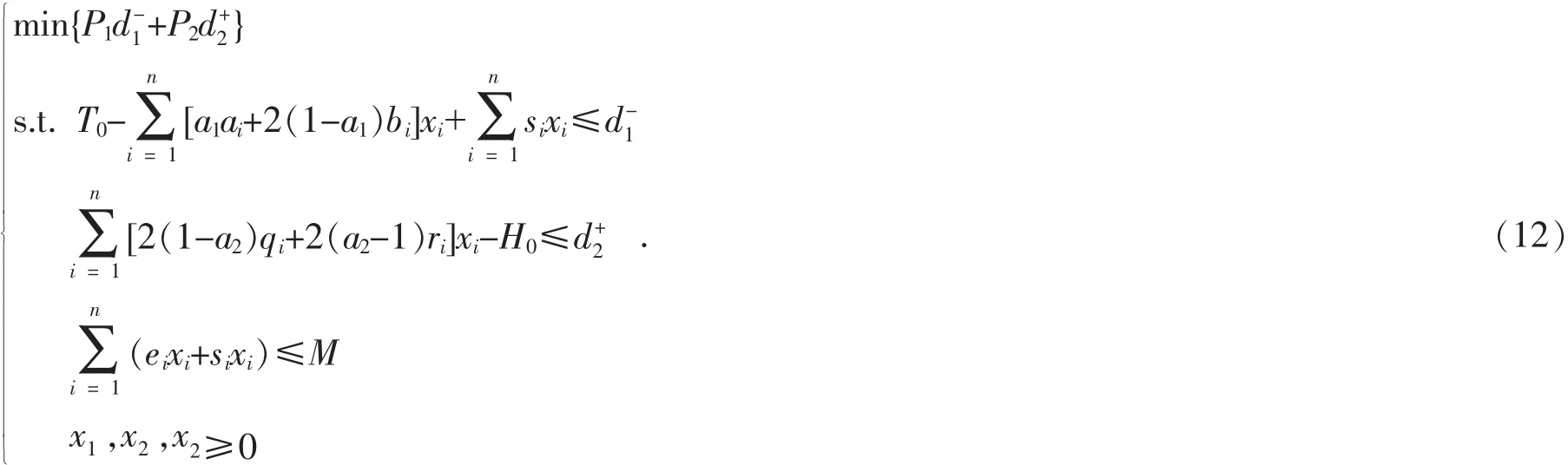
5 数值例子

例 某公司想投资A，B，C三种项目，公司现有总资金为1 000万元，决策者设定的收益预期T0=2 000万元.所能承受的最大损失H0=300万元，投资这3个项目的单位交易费si分别为1，2，5万元，假设单位收益ηi与单位风险是“之”字形不确定变量.为了清晰起见，建立表1.

因为ξi与ηi都是“之”字形不确定数，且目标函数及约束条件都是线性的，则模型（8）可以转化为确定形式（9）.经计算

则模型（10）转化为求解如下模型：

若预先给定的置信水平α1，α2=0.9，则模型（12）转化为求解如下模型

采用数学软件MATLAB编程求解模型（13），（14）运行结果见表2.

这个例子说明了用不确定规划方法解决不确定环境下投资收益与风险问题，不仅能减少投资者获取信息的费用，而且更加贴切于实际情况.

表1 相关数据

表2 求解结果

6 结论

投资问题是当今现实生活的热门话题，例如投资金融证劵市场、房地产、餐饮业及服装类项目.目前针对该问题的研究数据一般仅限于精确数据.而面对复杂多变的投资市场，数据的来源往往很不精确，例如单位收益与单位风险.用不确定变量来表示他们更能真实地反应实际情况.因此笔者所提出的解决不确定环境下投资问题的方法实用范围广，可操作性强，并具有一定的现实意义.

[1]LIU B D.Uncertainty Theory[M].Berlin：Springer-Verlag，2007.

[2]LIU B D.Uncertainty Theory：A Branch of Mathematics for Modeling Human Uncertainty[M].Berlin：Springer-Verlag，2010.

[3]LIU B D.Some Research Problems in Uncertainty Theory[J].Journal of Uncertainty Systems，2009，3（1）：3-10.

[4]LIU B D.Why is There a Need for Uncertainty Theory?[J].Journal of Uncertain Systems，2012，6（1）：3-10.

[5]GAO X.Some Properties of Continuous Uncertain Measure[J].International Journal of Uncertainty，Fuzziness and Knowledge-Based Systems，2009，17（3）：419-426.

[6]YOU C L.Some Convergence Theorems of Uncertain Sequences[J].Mathematical and Computer Modelling，2009，49（3-4）：482-487.

[7]LIU B D.Theory and Practice of Uncertain Programming[M].Berlin：Springer-Verlag，2009.

[8]LIU B D，CHEN X W.Uncertain Multiobjective Programming and Uncertain Goal Programming[J].Technical Report，2013.

[9]Liu Y K.Expected Value of Function of Uncertain Variables[J].Journal of Uncertain Systems，2010，4（3）：181-186.

（责任编辑 钮效鹍）

Investment Return and Risk Problems in Uncertain Environment

ZHAO Jian-hua1，LI Wei2，LIU Ya-na1，CAO Zhi-jun1
（1.School of Mathematics&Information Science；2.School of Economics&Management，Shijiazhuang University，Shijiazhuang，Hebei 050035，China）

Investment problems are described in uncertain environment when the unit profits and the unit risks are supposed to be uncertain variables.Then，with different criteria，two new models are constructed on the basis of uncertainty theory，i.e.，expected value goal programming model and chance constrained goal programming model.Moreover，with help of the operational law of uncertainty theory，the crisp equivalents are derived to solve the models more simply and faster.Finally，a numerical example is given for illustrating the rationality and effectiveness with uncertain programming to solve the uncertain investment problems.

investment problem；uncertainty theory；uncertain variable；uncertain programming；goal programming

O221

A

1673-1972（2015）03-0022-06

2014-10-10

石家庄学院自然科学基金（13YB001）

赵建华（1960-），女，福建安溪人，教授，主要从事不确定规划及应用研究.